Hypothesen für große Primzahlen haben sich für kleine Zahlensysteme bewährt

Die Twin-Prime-Hypothese ist eine der wichtigsten und komplexesten Fragen der Mathematik. Zwei Mathematiker lösten eine parallele Version dieses Problems für kleine numerische Systeme.

Am 7. September veröffentlichten zwei Mathematiker einen Beweis für eine Version eines der bekanntesten offenen Probleme der Mathematik. Das Ergebnis eröffnet eine neue Front in der Untersuchung der Hypothese der Doppelprimzahlen , die Mathematiker seit mehr als hundert Jahren plagt und mit einigen der tiefgreifendsten Eigenschaften der Arithmetik in Verbindung gebracht wird.

"Wir sind lange Zeit ins Schleudern geraten und wir haben nicht mehr genügend Ideen für diese Aufgabe. Daher ist es für jeden selbstverständlich, neue Ideen zu haben", sagte James Maynard , Mathematiker aus Oxford.

Die Twin-Prim-Hypothese gilt für Primpaare, die sich um 2 unterscheiden. Die Zwillinge sind die Zahlen 5 und 7. Und 17 und 19. Die Hypothese besagt, dass es unter natürlichen Zahlen eine unendliche Anzahl solcher Paare gibt. In den letzten zehn Jahren haben die Mathematiker erhebliche Fortschritte erzielt, sind jedoch noch weit von einer vollständigen Lösung des Problems entfernt.

Die Autoren der neuen Beweise, Will Savin von der Columbia University und Mark Shusterman von der University of Wisconsin in Madison, haben die Hypothese für eine kleinere, aber immer noch auffällige mathematische Welt bewiesen. Sie haben ihre Gültigkeit im Fall eines endlichen numerischen Systems bewiesen, in dem es nur wenige Zahlen gibt.

Solche Zahlensysteme werden als "endliche Felder" bezeichnet. Trotz ihrer geringen Größe behalten sie viele der mathematischen Eigenschaften bei, die unzähligen ganzen Zahlen innewohnen. Mathematiker versuchen Antworten auf Fragen der Arithmetik in endlichen Feldern zu finden und hoffen, diese Ergebnisse auf alle ganzen Zahlen zu übertragen.

"Der ultimative Traum, wenn auch ein bisschen naiv, ist, dass ein gutes Verständnis der Eigenschaften eines endlichen Feldes Licht in die Welt der ganzen Zahlen bringen kann", sagte Maynard.

Savin und Shusterman haben nicht nur die Hypothese der Zwillingsprimzahlen bewiesen, sondern auch ein noch überraschenderes Ergebnis hinsichtlich des Verhaltens von Primzahlen in kleinen numerischen Systemen gefunden. Sie haben die genaue Häufigkeit bewiesen, mit der die Doppelprimes in kleinen Intervallen auftreten - und dieses Ergebnis ermöglicht es, das Phänomen der Doppelprimes genau zu kontrollieren. Mathematiker träumen davon, mit gewöhnlichen Zahlen ähnliche Ergebnisse zu erzielen. Sie erforschen neue Beweise auf der Suche nach Ideen, die auf Primzahlen in einer Zahlenreihe anwendbar sind.

Eine neue Art von Prime

Die bekannteste Vorhersage der Twin-Prime-Hypothese ist das Vorhandensein einer unendlich großen Anzahl von Zahlenpaaren, die sich um 2 unterscheiden. Diese Aussage ist jedoch allgemeiner. Es heißt, dass es unendlich viele Primzahlen gibt, die sich um 4 (z. B. 3 und 7), um 14 (293 und 307) oder um eine von Ihnen angegebene Zahl unterscheiden.

Alfons de Polignac machte diese Annahme in seiner modernen Form im Jahre 1849. In den nächsten 160 Jahren kamen die Mathematiker nicht viel mit ihm voran. Im Jahr 2013 ist das Eis jedoch gebrochen oder zumindest stark geknackt. In diesem Jahr hat Zhang Ethan die Anwesenheit einer unendlich großen Anzahl von Primzahlenpaaren nachgewiesen, die sich um nicht mehr als 70 Millionen unterscheiden. Nächstes Jahr haben andere Mathematiker, darunter Maynard und Terry Tao , diese Lücke ernsthaft geschlossen. Der aktuelle Datensatz ist der Beweis für die Existenz einer unendlich großen Anzahl von Primzahlenpaaren, die sich um nicht mehr als 246 voneinander unterscheiden.

Danach ließen die Fortschritte jedoch nach. Mathematiker verstehen die Notwendigkeit einer völlig neuen Idee, um dieses Problem vollständig zu lösen. Und endliche Zahlensysteme sind ein guter Ort, um nach dieser Idee zu suchen.

Um ein endliches Feld zu erstellen, müssen Sie zunächst eine endliche Teilmenge von Zahlen aus natürlichen Zahlen extrahieren. Sie können beispielsweise die ersten fünf Zahlen (oder eine beliebige Primzahl) verwenden. Und anstatt wie üblich Zahlen in einer Zahlenreihe darzustellen, stellen Sie sich ein neues Zahlensystem in Form eines Zifferblatts vor.

Wie Sie vielleicht erraten haben, beginnt das Rechnen auf engstem Raum. Was ist 4 + 3 in einem endlichen numerischen System, das aus fünf Elementen besteht? Wir beginnen mit 4, zählen drei Divisionen im Uhrzeigersinn und kommen zu 2. Subtraktion, Multiplikation und Division funktionieren auf ähnliche Weise.



Aber es gibt nur einen Haken. In endlichen Feldern ist die übliche Definition einer Primzahl nicht sinnvoll. Im letzten Feld wird jede Zahl durch eine andere geteilt. Zum Beispiel ist 7 normalerweise nicht durch 3 teilbar. Auf einem letzten Feld von fünf Elementen ist es jedoch teilbar. Das liegt daran, dass in diesem letzten Feld die Zahl 7 der Zahl 12 entspricht - beide enden bei der 2-Markierung des Zifferblatts. Daher ergibt 7 geteilt durch 3 das Gleiche wie 12 geteilt durch 3 - und 12 geteilt durch 3 ergibt 4.

Daher bezieht sich die Hypothese der Doppelprimzahlen für endliche Felder auf einfache Polynome - solche mathematischen Ausdrücke wie zum Beispiel x ² + 1.

Angenommen, Ihr letztes Feld enthält die Zahlen 1, 2 und 3. Diese Zahlen sind die Koeffizienten des Polynoms in diesem endlichen Feld, und das "einfache" Polynom ist eines, das nicht in Polynomfaktoren zerlegt werden kann. Daher ist x ² + x + 2 einfach, da es nicht faktorisiert werden kann, aber x ² - 1 nicht: Dies ist das Produkt von (x + 1) und (x - 1).

Nachdem einfache Polynome definiert wurden, stellt sich natürlich die Frage nach einfachen Doppelpolynomen - Paaren von Polynomen, die einfach sind und sich durch einen festen Wert unterscheiden. Zum Beispiel ist das Polynom x ² + x + 2 einfach, wie x ² + 2x + 2. Sie unterscheiden sich durch x.

Die Hypothese einfacher Doppelpolynome für endliche Felder zeigt die Existenz einer unendlich großen Anzahl von Paaren einfacher Doppelpolynome, die sich nicht nur um x, sondern um einen beliebigen Wert unterscheiden.

Ordentliche Schnitte

Die Konzepte endlicher Felder und einfacher Polynome mögen weit hergeholt und für die Untersuchung der Eigenschaften von Zahlen nutzlos erscheinen. Aber sie sehen aus wie ein Hurrikansimulator - ein Universum für sich, das Vorstellungen über Phänomene in einer großen Welt vermittelt.

"Es gibt eine uralte Analogie zwischen Ganzzahlen und Polynomen, mit der Sie potenziell äußerst komplexe Probleme im Zusammenhang mit Ganzzahlen in Aufgaben im Zusammenhang mit Polynomen umwandeln können, die ebenfalls potenziell komplex sind, aber möglicherweise einfacher zu lösen sind", sagte Shusterman.

Finite Felder wurden 1940 berühmt, als Andre Weil die genaue Methode entwickelte, um die Arithmetik von kleinen Zahlensystemen in die Arithmetik von ganzen Zahlen zu übersetzen. Weil nutzte diese Verbindung mit erstaunlichen Ergebnissen. Er erwies sich als das vielleicht wichtigste mathematische Problem - die Riemannsche Hypothese - für den Fall einer Reihe von Kurven über endlichen Feldern (dieses Problem ist unter dem Namen der Riemannschen geometrischen Hypothese bekannt). Dieser Beweis, zusammen mit einer Reihe zusätzlicher Weyl-Hypothesen, machte endliche Felder zu einer reichen Landschaft für mathematische Entdeckungen.

Weils Schlüsselidee war, dass in endlichen Feldern geometrische Techniken verwendet werden können, um Antworten auf Fragen zu Zahlen zu finden. „Dies ist ein Merkmal von endlichen Feldern. Viele der Aufgaben, die Sie lösen möchten, können geometrisch umformuliert werden “, sagte Shusterman.

Um zu verstehen, wie Geometrie in einer solchen Umgebung erscheint, stellen Sie sich jedes Polynom als einen Punkt im Raum vor. Die Koeffizienten eines Polynoms dienen als Koordinaten zur Bestimmung seiner Position. Zurückkehrend zu unserem letzten Feld von 1, 2 und 3 befindet sich das Polynom 2x + 3 am Punkt (2, 3) des zweidimensionalen Raums.

Aber auch im einfachsten endlichen Raum gibt es unendlich viele Polynome. Komplexere Polynome können durch Erhöhen des Exponenten des größten Exponenten oder des Expressionsgrades erzeugt werden. In unserem Fall wird das Polynom x ² - 3x - 1 durch einen Punkt im dreidimensionalen Raum dargestellt. Das Polynom 3x ⁷ + 2x ⁶ + 2x ⁵ - 2x ⁴ - 3x ³ + x ² - 2x + 3 wird durch einen Punkt im achtdimensionalen Raum dargestellt.

In der neuen Arbeit repräsentiert dieser geometrische Raum alle Polynome eines bestimmten Grades für ein bestimmtes endliches Feld. Die Frage stellt sich wie folgt: Gibt es eine Möglichkeit, alle Punkte zu isolieren, die einfache Polynome bezeichnen?

Die Strategie von Savin und Shusterman besteht darin, den Raum in zwei Teile zu teilen. In einem Teil gibt es alle Punkte, die Polynomen mit einer geraden Anzahl von Faktoren entsprechen. Im anderen Fall entsprechen alle Punkte Polynomen mit einer ungeraden Anzahl von Faktoren.



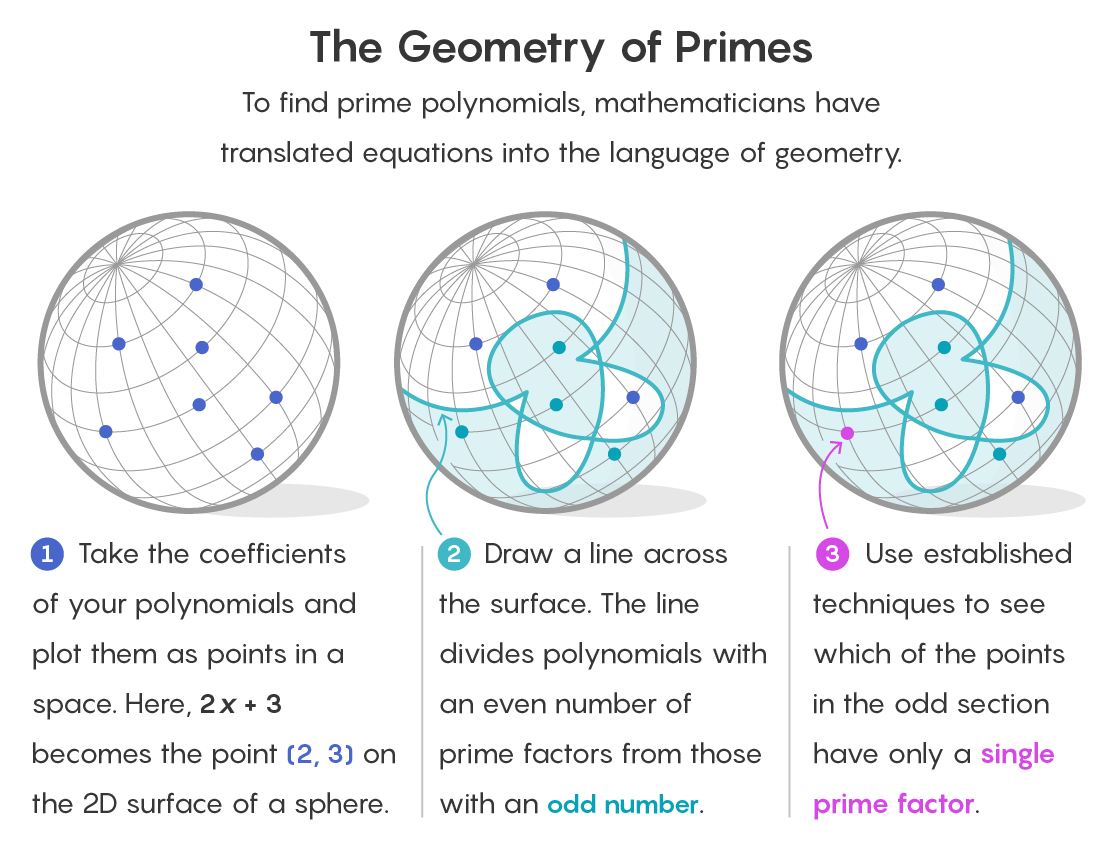
Dies vereinfacht bereits die Aufgabe. Die Hypothese einfacher Doppelpolynome für endliche Felder gilt nur für Polynome mit einem Faktor (genau wie eine Primzahl einen Faktor hat, ist sie selbst). Und da die Zahl 1 ungerade ist, kann ein Teil des Raums, der Polynome mit einer geraden Anzahl von Faktoren enthält, sofort verworfen werden.

Der Trick ist, Division zu verwenden. Bei einem zweidimensionalen Objekt, zum Beispiel der Oberfläche einer Kugel, wird es durch eine eindimensionale Kurve in zwei Hälften geteilt - genau wie der Äquator die Oberfläche der Erde schneidet. Ein Objekt mit einer großen Anzahl von Dimensionen kann immer mit einem Objekt mit einer um eins geringeren Anzahl von Dimensionen geschnitten werden.

Aber diese Formen mit weniger Dimensionen, die den Raum der Polynome teilen, sind überhaupt nicht so elegant wie der Äquator. Sie werden nach einer mathematischen Formel gezeichnet, die als Mobius-Funktion bezeichnet wird . Am Eingang erhält man ein Polynom und am Ausgang 1, wenn das Polynom eine gerade Zahl von Primfaktoren hat, -1, wenn es eine ungerade Zahl hat und 0, wenn es faktorisiert ist (da 16 in 2 × zerlegt werden kann) 2 × 2 × 2).

Die von der Möbius-Funktion gezeichneten Kurven biegen und verdrehen sich wie verrückt und kreuzen sich an vielen Stellen. Diese Orte, Singularitäten genannt, sind besonders schwierig zu analysieren (sie entsprechen Polynomen, die in mehrere identische Primfaktoren zerlegt werden können).

Die grundlegende Neuerung von Savin und Shusterman war, dass sie den genauen Weg fanden, um Loops mit weniger Messungen in kürzere Segmente zu schneiden. Diese Segmente waren leichter zu lernen als die gesamte Schleife.

Nachdem Savin und Shusterman einen Katalog von Polynomen mit einer ungeraden Anzahl von Primfaktoren zusammengestellt hatten - und dies war der schwierigste -, standen sie vor der Aufgabe zu bestimmen, welche einfach und welche Zwillinge sind. Zu diesem Zweck verwendeten sie verschiedene Formeln, die von Mathematikern verwendet wurden, um Primzahlen unter gewöhnlichen zu studieren.

Savin und Shusterman verwendeten ihre Technik, um zwei wichtige Punkte in Bezug auf einfache Polynome in bestimmten endlichen Feldern zu beweisen.

Erstens ist die Hypothese der Zwillingsprimzahlen in endlichen Feldern wahr: Es gibt unendlich viele Paare von Zwillingspolynomen, die sich um einen bestimmten Wert unterscheiden.

Zweitens, und was noch wichtiger ist, liefert diese Arbeit eine genaue Zählung der Anzahl einfacher Doppelpolynome, die unter Polynomen einer bestimmten Ordnung gefunden werden können. Dies ist analog zu wissen, wie viele Doppelprimzahlen sich in einem ausreichend langen Intervall auf einer Zahlenreihe befinden - und dies ist nur der Traum von Mathematikern.

"Dies ist die erste Arbeit, die eine quantitative Analogie dessen liefert, was für ganze Zahlen gelten sollte, und dies ist ein wirklich herausragendes Ergebnis", sagte Ziv Rudnik von der Universität Tel Aviv. "Bisher ist nichts dergleichen passiert."

Der Beweis von Savin und Schusterman zeigt, dass die Mathematiker fast 80 Jahre nachdem Andre Weil die Riemannsche Hypothese für Kurven über endliche Felder bewiesen hat, immer noch hartnäckig in diese Richtung gehen. Jetzt wenden sich Mathematiker, die sich mit der Twin-Prime-Hypothese befassen, der Arbeit von Savin und Shusterman zu und geben ihnen vielleicht eine tiefe Quelle der Inspiration.