Was ist das nächste Mitglied ...? - Wir suchen nach einer Formel für den n-ten Term der Sequenz, die Funktionen und die Z-Transformation generiert

Sie können die Datei mit dem Code und den Daten im Originalbeitrag auf meinem Blog herunterladen

Wolfram Language bietet vier großartige Funktionen: FindSequenceFunction , RSolve , DifferenceRootReduce und FindFormula . In diesem Artikel werden ihre Funktionen und Funktionen FindLinearRecurrence , die in engem Zusammenhang mit ihnen stehen, um nach linearen FindLinearRecurrence Rekursionsparametern (Koeffizienten einer linearen Rekursionsgleichung) zu suchen, die die GeneratingFunction und ZTransform Z-Transformationsfunktionen generieren.

Die erste Funktion , FindSequenceFunction, sucht nach einem Ausdruck für das n-te Element anhand einer Folge von Zahlen, ohne dass weitere Informationen erforderlich sind.

 Hold @ FindSequenceFunction[{1, 1, 2, 3, 5, 8, 13}, n] 

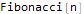
 FindSequenceFunction[ {-2, 4Sqrt[Pi], -16, 16Sqrt[Pi], -128/3, 32Sqrt[Pi], -1024/15, 128Sqrt[Pi]/3, -8192/105, 128Sqrt[Pi]/3}, n] 

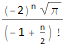Die zweite Funktion , RSolve, löst Wiederholungsgleichungen verschiedener Typen. Elemente können so aussehen $$$a [f [n]]$, $$$a [f [f [n]]]$, $$$a [f [f [\ text {...} f [n] \ text {...}]]$, wobei f die Form hat: n + A (arithmetische Differenzgleichungen), B * n - geometrische oder q-Differenzgleichungen), B * n + a (arithmetisch-geometrische funktionale Differenzgleichungen), B * n ^ d (geometrische Potenzfunktion) Differenzgleichungen), (A * n + B) / (C * n + D) (lineare gebrochene funktionale Differenzgleichungen).

 RSolve[ { a[n + 3]==2 * a[n], a[1]==α, a[2]==β, a[3]==γ }, a, n ] 

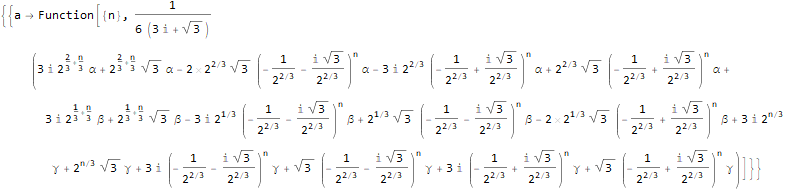
 RSolve[ { v[n]==(2 * Pi * v[n - 2]) / n, v[2]==Pi, v[3]==(4 * Pi) / 3 }, v @ n, n ] 

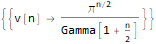Die dritte Funktion - DifferenceRootReduce - sucht nach einer Wiederholungsrelation für eine Folge von Zahlen, deren n-tes Element eine bestimmte Form hat.

 DifferenceRootReduce[-2 * n * Pi * Factorial[(n * 2) - 1], n ] 

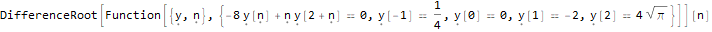
 RSolve[ { (-8 * y[n]) + n * y[2 + n]==0, y[-1]==1/4, y[0]==0, y[1]==-2, y[2]==4Sqrt[Pi] }, y, n ] 

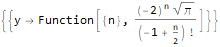
Diese Funktion kann viel mehr, zum Beispiel Identitäten in Bezug auf Sequenzen überprüfen, zum Beispiel:

 DifferenceRootReduce[Fibonacci[2 * n]==Fibonacci[n] * LucasL[n], n] 

Hier ist LucasL eine Folge von Luc-Zahlen (dies ist in der Tat eine Fibonacci-Folge, nur die ersten Mitglieder sind nicht 1, 1, sondern 1, 3).

 Hold @ DifferenceRootReduce @ LucasL @ n 

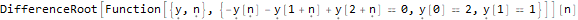
 DifferenceRootReduce[LucasL[n]==Fibonacci[n - 1] + Fibonacci[n + 1]] 

Wie finde ich eine Wiederholungsformel für eine Sequenz?

Die Suchmethode für ein gemeinsames Element einer Sequenz basiert häufig auf der Notwendigkeit, eine Wiederholungsgleichung auszuwählen.

Es kann in etwa so aussehen: Suchen wir das n-te Mitglied der Sequenz im Formular $$$f [n] = \ sum_ {i = 1} ^ ka [i] f [n-i]$. Lassen Sie uns die ersten Mitglieder der Sequenz haben:

 sequence = {1, 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461} 

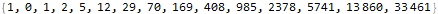
Versuchen wir, einen Ausdruck für den n-ten Ausdruck in der Form zu finden $$$f [n] = \ sum_ {i = 1} ^ 1a [i] f [n-i] = a [1] f [n-1]$:

 seauenseEq1 = MovingMap[ Function[ Dot[Part[#, 1;;1], {a @ 1}]==Part[#, -1] ], sequence, 1 ] 

 Hold @ Solve @ seauenseEq1 

Wie Sie sehen, gibt es keine Lösungen.

Versuchen wir jetzt im Formular zu suchen $$$f [n] = \ sum_ {i = 1} ^ 2a [i] f [n-i] = a [1] f [n-1] + a [2] f [n-2]$:

 seauenseEq2 = MovingMap[ Function[ Dot[Part[#, 1;;2], {a @ 1, a @ 2}]==Part[#, -1] ], sequence, 2 ] 

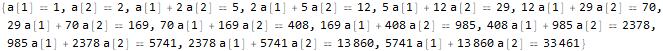
 Hold @ Solve @ seauenseEq2 

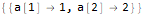
Wie wir sehen, hat es sich herausgestellt. Daher hat der n-te Term die Form: $$$f [n] = f [n-1] + 2f [n-2]$.

Tatsächlich gibt es eine integrierte FindLinearRecurrence Funktion, mit der Sie eine lineare Rekursion finden können, ähnlich wie wir es gerade getan haben:

 Hold @ FindLinearRecurrence @ sequence 

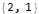
Mit der LinearRecurrence Funktion können LinearRecurrence die Sequenz erweitern:

 LinearRecurrence[{2, 1}, sequence[[1;;2]], 50] 

Oder kombinieren Sie alles zu einer Zeile, indem Sie eine Funktion konstruieren, die: die Sequenz erweitert, eine Differenzgleichung erzeugt und eine allgemeine Formel für den n-ten Term findet:

 sequenseExtension[list_, n_] := Module[ {lr, eq}, lr = FindLinearRecurrence @ list; eq = Flatten[ { a[k]==Total[ Table[ a[k + -i] * Part[lr, i], {i, 1, Length @ lr} ] ], Table[a[i], list[[i]]], {i, 1, Length @ lr}] } ]; <| "" -> eq, "" -> FullSimplify[a[k] /. Part[RSolve[eq, a, k], 1]], "" -> LinearRecurrence[lr, Part[list, Span[1, Length[lr]]], n] |> ]; 

 Hold @ sequenseExtension[{1, 1, 2, 3, 5}, 20] 

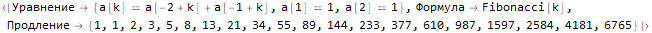
 Hold @ sequenseExtension[{1, 2, 2, 1, 1, 2, 2, 1}, 20] 

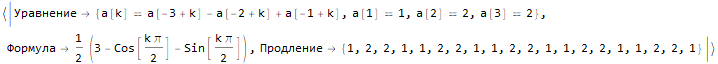
 Hold @ sequenseExtension[ {1, 0, -1, 0, 2, 0, -2, 0, 3, 0, -3, 0, 4, 0, -4}, 25 ] 

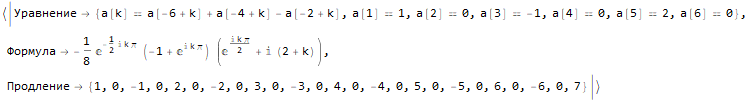
Wie finde ich die Formel für das n-te Glied einer Sequenz?

Z-Konvertierung

Die Z-Transformation besteht in der Berechnung einer Reihe von Formen $$$\ sum_ {n = 0} ^ {\ infty} f (n) z ^ {- n}$von der diskreten Funktion $$$f (n)$. Diese Transformation ermöglicht es uns, die Wiederholungsgleichung zum Einstellen der Sequenz auf die Gleichung für das Bild der Funktion zu reduzieren $$$f (n)$Dies ähnelt der Laplace-Transformation, bei der Differentialgleichungen auf algebraische Gleichungen reduziert werden.

So funktioniert es:

 Grid[ Transpose[ Function[ { #, Map[TraditionalForm, Map[FullSimplify, ZTransform[#, n, z]]] } ][ { f[n - 2], f[n - 1], f @ n, f[n + 1], f[n + 2] } ] ], Background -> White, Dividers -> All ] 

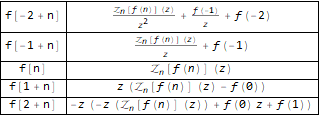
Schauen wir uns ein Beispiel an, nehmen wir die bekannte Fibonacci-Sequenz:

 fibonacciEq = f[n]==f[n - 1] + f[n - 2]; initialConditions = {f[1] -> 1, f[2] -> 1}; 

Es ist klar, dass es in der unten gezeigten Form umgeschrieben werden sollte, damit Konstruktionen wie $$$f (-1)$nach dem Anwenden der Z-Transformation.

 fibonacciEq = f[n + 2]==f[n + 1] + f[n]; initialConditions = {f[0] -> 1, f[1] -> 1}; 

Wir führen die Z-Transformation durch:

 fibonacciEqZTransformed = ReplaceAll[fibonacciEq, pattern:f[__] :> ZTransform[pattern, n, z]] 

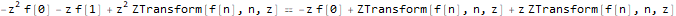
Wir lösen die Gleichung für das Bild der Funktion f - ZTransform [f [n], n, z]:

 fZTransformed = ReplaceAll[ ZTransform[f @ n, n, z], Part[Solve[fibonacciEqZTransformed, ZTransform[f @ n, n, z]], 1] ] 

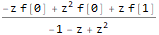
Wir führen die inverse Z-Transformation durch und ersetzen gleichzeitig die Anfangsbedingungen (wir ersetzen n durch n-1 im Endausdruck, damit unsere Sequenz die richtige Indizierung hat (vom ersten, nicht vom Nullterm):

 ReplaceAll[InverseZTransform[fZTransformed /. initialConditions, z, n], n -> (n - 1) ] 

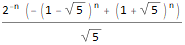
Dies kann natürlich automatisiert werden, indem Sie Ihr eigenes RSolve-Gegenstück erstellen:

 myRSolve[eq_, initials_, f_, n_] := Module[ {z, initialsInner, eqZTransformed, fZTransformed}, initialsInner = ReplaceAll[initials, f[x_] :> f[x - 1]]; eqZTransformed = ReplaceAll[eq, pattern:f[__] :> ZTransform[pattern, n, z]]; fZTransformed = ReplaceAll[ZTransform[f @ n, n, z], Part[Solve[eqZTransformed, ZTransform[f @ n, n, z]], 1] ]; FullSimplify[ InverseZTransform[fZTransformed /. initialsInner, z, n] /. n -> (n - 1) ] ]; 

 myRSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]) }, {f[1] -> 20, f[2] -> 0}, f, n ] 

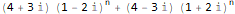
 RSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]), f[1]==20, f[2]==0 }, f, n ] 

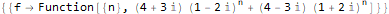
Aber natürlich bietet RSolve viel mehr Möglichkeiten zum Lösen einer Vielzahl von diskreten Gleichungen, auf die wir nicht näher eingehen werden:

 RSolve[a[n]==(n * a[n]) + n, a, n], RSolve[ { a[n + 1]==(2 * a[n]) + (3 * a[n]) + 4, a[0]==0 }, a, n ], RSolve[ y[n + 1 * 3]==(2 * y[n + 1 * 6]) + n * 2, y, n ] 

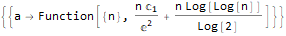
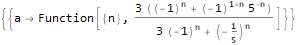
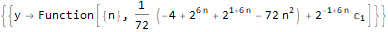
Funktionen generieren

Sequenzfunktion generieren $$$a (n)$Das ist eine solche Funktion $$$G (x)$, dessen Erweiterung in der Taylor-Reihe (oder allgemeiner Laurent) die Form hat - $$$G (x) = \ sum_ {i = 0} ^ {\ infty} a (n) x ^ n$. Mit anderen Worten, die Potenzkoeffizienten von x bei der Erweiterung der Funktion in einer Reihe bestimmen unsere Sequenz.

Funktion sagen $$$G (x) = \ frac {1} {1-x}$ist eine generierende Funktion der Folge 1, 1, 1, 1, ...:

 Series[1 / (1 + -x), {x, 0, 10}] 

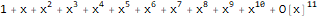
Eine Funktion $$$G (x) = \ frac {1} {1-x-x ^ 2}$ist eine generierende Funktion der Fibonacci-Sequenz 1, 1, 2, 3, 5, 8, 13, ...:

 Series[(1 * 1) + (-x) + -(x * 2), {x, 0, 10} ] 

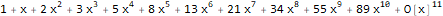
Es gibt auch eine Art Erzeugungsfunktion - eine exponentielle Erzeugungsfunktion, die für die Sequenz $$$a (n)$hat die Form - $$$G (x) = \ sum_ {i = 0} ^ {\ infty} \ frac {a (n)} {n!} X ^ n$.

Angenommen, für die Sequenzen 1, 1, 1, 1 ... und 1, 1, 2, 3, 5, 8, 13 ... sind die Exponentialerzeugungsfunktionen wie folgt: $$$e ^ x$und $$$\ frac {1} {\ sqrt {5}} e ^ {- \ frac {2x} {1+ \ sqrt {5}}} \ left (e ^ {\ sqrt {5} x} -1 \ right)$:

 ReplaceAll[Normal[Series[E ^ x, {x, 0, 10}]], Power[x, n_] :> ((x ^ n) * Factorial[n]) ] 

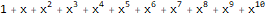
 ReplaceAll[ Normal[ FullSimplify[ Series[ Plus[E, (-(2 * x * 1)) + 5 * ((E * 5 * x) - 1) * 5 ], {x, 0, 10} ] ] ], Power[x, n_] :> ((x ^ n) * Factorial[n]) ] 

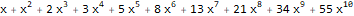
Die produzierende Funktion in Wolfram Language kann durch zwei Funktionen gefunden werden - GeneratingFunction und FindGeneratingFunction (exponentiell mit ExponentialGeneratingFunction ):

 GeneratingFunction[-(m * Factorial[n]), {n, m}, {x, y}] 

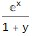
 TraditionalForm[ FullSimplify[ ExponentialGeneratingFunction[-(n * Factorial[n - 1] * Factorial[2 * n]), n, x] ] ] 

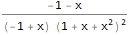
Es gibt viele Methoden, um mithilfe von Generierungsfunktionen ein gemeinsames Mitglied einer Sequenz zu finden. Wir werden nicht im Detail darauf eingehen, sagen wir, auf der Website von genfunc.ru finden Sie nur eine gute Theorie.

Eine der Methoden ähnelt der Z-Transformation:

 generatingFEq = ReplaceAll[ f[n + 2]==f[n + 1] + f[n], pattern:f[__] :> GeneratingFunction[pattern, n, z] ], generatingF = ReplaceAll[ GeneratingFunction[f @ n, n, z], Part[Solve[generatingFEq, GeneratingFunction[f @ n, n, z]], 1] ], nthTerm = SeriesCoefficient[generatingF, {z, 0, n}], FullSimplify[ ReplaceAll[ReplaceAll[nthTerm, {f[0] -> 1, f[1] -> 1}], n -> (n - 1) ], GreaterEqual[n, 1] ] 

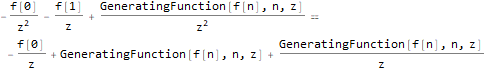
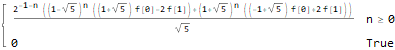
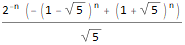
OEIS - Online Integer Sequence Encyclopedia und Integration mit Wolfram Language

Eine absolut atemberaubende Sammlung von Zahlensequenzen ist im Internet verfügbar - OEIS (Online Encyclopedia of Integer Sequences) . Es wurde von Neil Sloan während seiner Forschungskarriere bei AT & T Labs erstellt. OEIS speichert Informationen zu ganzzahligen Sequenzen, die sowohl für Amateure als auch für Profis in den Bereichen Mathematik, Kombinatorik, Zahlentheorie, Spieltheorie, Physik, Chemie, Biologie und Informatik von Interesse sind. Derzeit werden dort 329085 Sequenzen gesammelt. Ein Datensatz in OEIS enthält die ersten Elemente einer Sequenz, Schlüsselwörter, mathematische Beschreibung, Nachnamen der Autoren, Links zur Literatur; Es besteht die Möglichkeit, eine musikalische Darstellung der Sequenz zu zeichnen oder abzuspielen. Eine Suche in der Datenbank kann nach Stichwörtern und nach Teilfolgen erfolgen.

In letzter Zeit wurde die Integration in diese Datenbank in der Wolfram-Sprache veröffentlicht (bei der Verwendung ist es wichtig zu verstehen, dass dies eine Benutzerentwicklung ist - in letzter Zeit können Sie Ihren Code in das Wolfram Function Repository hochladen). Geben Sie einfach die Nummer der Sequenz ein, die Sie interessiert, oder eine Liste von Nummern.

 OEISSequenceData = ResourceFunction @ "OEISSequenceData"; OEISSequence = ResourceFunction @ "OEISSequence"; 

ResourceFunction ["OEISSequence"] - gibt einfach die ersten Mitglieder der Sequenz zurück:

 Hold @ OEISSequence @ "A666" 

ResourceFunction ["OEISSequenceData"] - gibt einen Datensatz mit vollständigen Informationen aus der Datenbank aus:

 sequenceData[666] = OEISSequenceData[666, "Dataset"] 

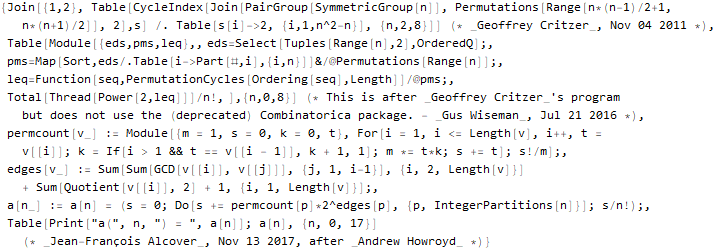
Angenommen, Sie können den Wolfram-Sprachcode "herausziehen":

 Hold @ Normal @ sequenceData[666]["CodeWolframLanguageStrings"] 

Oder eine Reihe zufällig ausgewählter Sequenzen mit Informationen, die für sie von Interesse sind:

 randomSequences = Dataset @ Map[ Normal, OEISSequenceData[RandomInteger[{1, 300000}, 10], "Dataset"] ]; 

 Function[ Framed[#, FrameStyle -> None, FrameMargins -> 5, Background -> White] ][ Grid[ Join[ { Map[Style[#, Bold, 18]&, {"", "", "", " ", "  "} ] }, Map[ Function[ Map[ Function[ TextCell[#, LineIndent -> 0, FontSize -> 12, FontFamily -> "Open Sans Light"] ], { Style[Part[#, 1], 16], Row[Part[#, 4], "\n"], Row[Part[#, 3], "\n"], Style[Row[Part[#, 2], "; "], 10], ListLinePlot[Part[#, 2], ImageSize -> Full] } ] ], Values @ Normal @ randomSequences[All, {"Name", "Sequence", "References", "Formulae"}] ] ], Dividers -> {{None, {LightGray}, None}, {None, {LightGray}, None}}, ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"], ItemSize -> {{15, 25, 10, 15, 15}, Automatic}, Alignment -> {Left, Center}, Background -> {None, {LightOrange, White}} ] ] 

Suchen Sie nach einer möglichen Formel

Abschließend möchte ich die FindFormula Funktion erwähnen, die auf der Grundlage einer bestimmten Anzahl von Zahlen eine Formel erstellt, die diese beschreiben kann. Wir können die Abhängigkeiten akzeptieren, Sie können eine Menge aus verschiedenen Funktionsklassen auswählen.

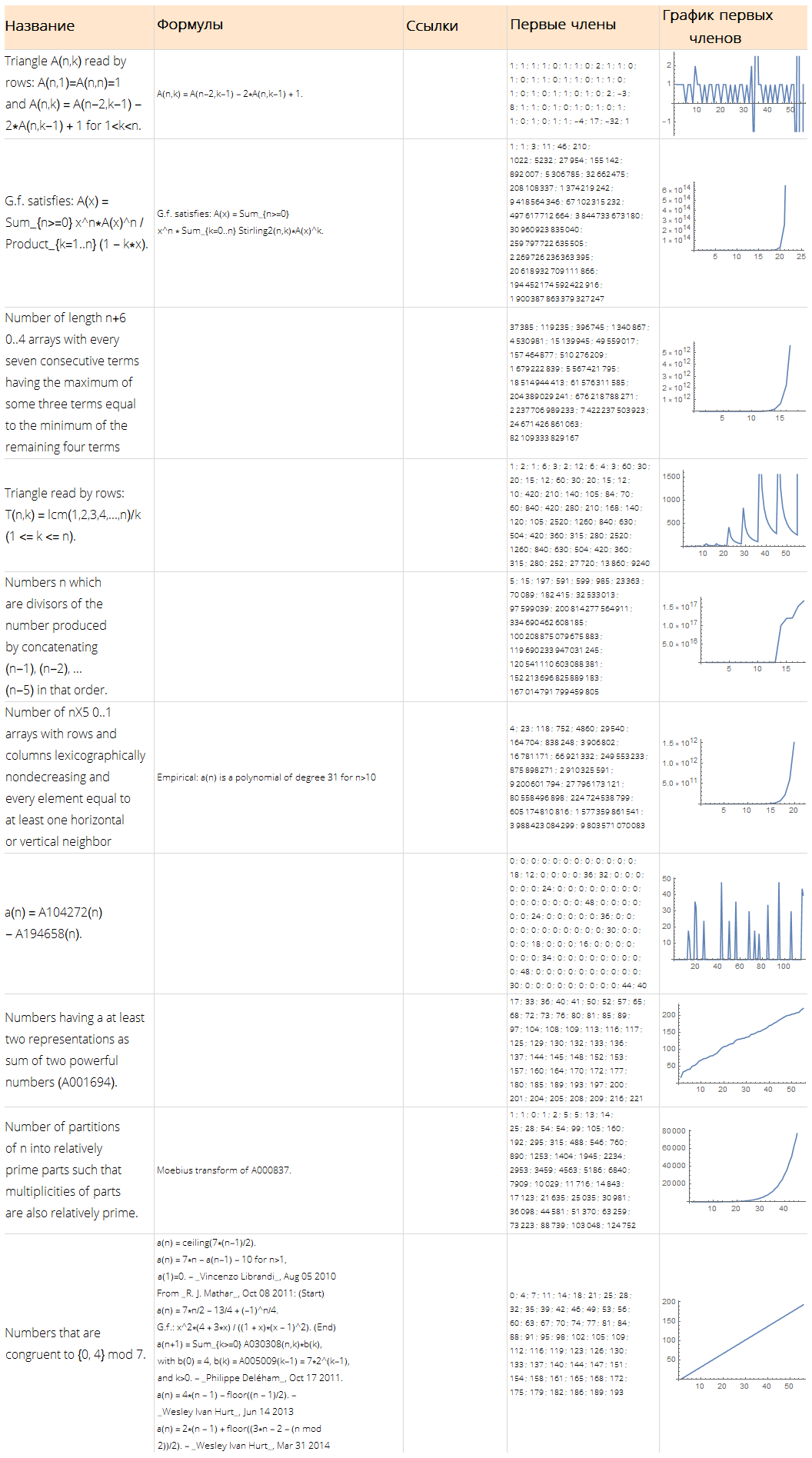
 data = Table[ { x, Sin[2 * x] + Cos[x] + RandomVariate[NormalDistribution[0, 0.2]] }, {x, RandomReal[{-10, 10}, 1000]} ]; ListPlot[data, Background -> White, ImageSize -> 600] 

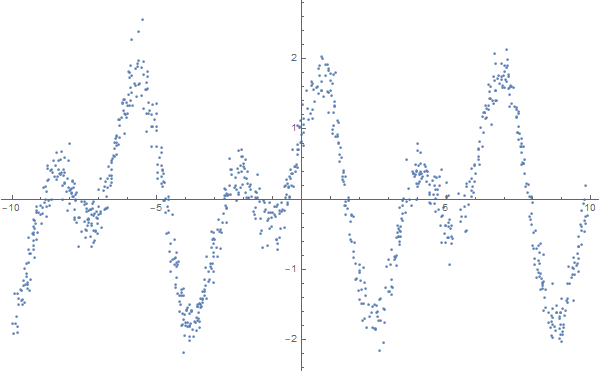
 formulas = FindFormula[data, x] 

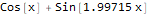
Wie Sie sehen, hat Wolfram Language eine Funktion ausgewählt, die der sehr nahe kommt, auf deren Grundlage "verrauschte" Daten erstellt wurden, nämlich - Sin [2x] + Cos [x]:

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], Gray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ] 

Sie können weitere Abhängigkeiten erstellen, z. B. 10:

 formulas = FindFormula[data, x, 10] 

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], LightGray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ] 

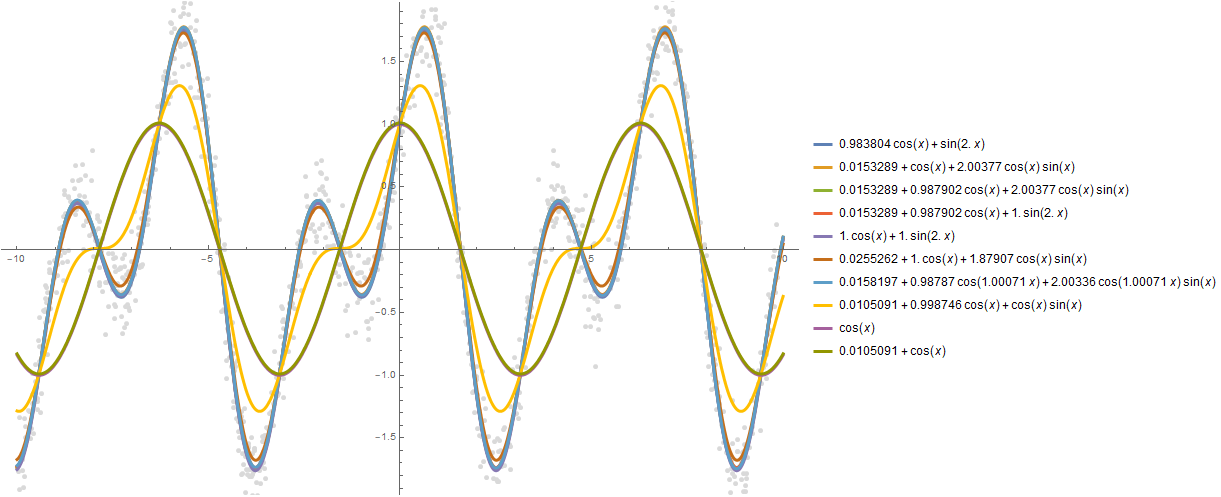
Es ist anzumerken, dass es eine ähnliche Funktion in der Funktionalität gibt, die nach einer Wahrscheinlichkeitsverteilung sucht - FindDistribution .

Für die Zusammenarbeit - schreibe eine persönliche Nachricht auf Habré oder in meiner VKontakte-Gruppe .
YouTube-Kanal - Webinare und Schulungsvideos.
Anmeldung für neue Kurse . Online-Kurs fertig.