👨‍🏫 🤲 👩🏻‍⚖️ Fügen Sie dem Roboter Augen hinzu 🔢 ⛏️ 🧖

Roboter muss man manchmal auch etwas zu verpassen. Das ist keine Augen wie ein Roboter ohne Arme. Im wahrsten Sinne des Wortes. Wenn der Roboter nicht weiß, wo der Leckerbissen liegt, kann er ihn schließlich nicht mit seinen Roboterarmen erreichen. Oder andere Manipulatoren.

zum Umschalten zwischen Robotersystem Koordinaten und 3D-IC-Kamera In diesem Artikel schauen wir uns an, wie der Roboter kalibrieren zu können.

Schritt 1. Nehmen Sie den Roboter

Wir werden Dobot-Magier Gegenstände bewegen lassen. Beobachten Sie, wie es Objekte bewegen wird - Intel Realsense D435. Und das Kalibrierungsobjekt muss eine rote Kugel sein.

So sehen sie zusammen aus.

Die rote Kugel ist nicht nur so gewählt, dass ~~jemand den Weihnachtsbaum schmücken soll~~ . Rot - damit es leicht im Bild zu finden ist (ohne ein anderes Netzwerk zu erlernen). Kugel - um den Mittelpunkt im Bild genauer zu berechnen. Aber wir werden später darauf zurückkommen.

Schritt 2. Wo der Roboter den Ball bewegt

Der Kalibrierungsalgorithmus kann wie folgt beschrieben werden:

Generieren Sie eine Liste von Positionen im Raum
Der Roboter bewegt den Ball auf der Liste, Aufnahmen mit ihm
Für jedes Bild finden wir die Koordinaten des Balls
Wir berechnen die Umrechnung von Kamerakoordinaten in Roboterkoordinaten

Die Positionen sollten so gewählt werden, dass sie so viel Platz wie möglich einnehmen. Der Ball ist besser, nicht ein wenig zu nehmen, wird die Genauigkeit der Kalibrierung zu reduzieren.

Wir werden hier nicht im Code führen die Kalibrierung zu schreiben, da auch sie ist abhängig von dem Roboter, Kamera, einer Umgebung, in der alles getan wird (zum Beispiel wir in ROS taten). Wichtig ist, dass Sie für die weitere Kalibrierung Fotos mindestens im manuellen Modus aufnehmen, Schritte senden, um den Roboter an Positionen zu schicken und Fotos zu speichern.

Die einzige Voraussetzung ist, dass die relativen Positionen der Kamera und des Roboters die ganze Zeit unverändert bleiben. Wir empfehlen außerdem, dass Sie sofort den zweiten Satz von Bildern zur Validierung aufnehmen, um zu bewerten, wie genau die Kalibrierung berechnet wurde.

Schritt 3. Holen Sie sich die Koordinaten

Wir kennen die Koordinaten des Manipulators, da wir den Roboter speziell an die in der Liste angegebenen Positionen schicken. Für Roboter mit einer großen Anzahl von Freiheitsgraden müssen Sie mehr Parameter angeben, aber in unserem 4-Achsen-Roboterarm wird die Position eindeutig durch die Koordinaten der Spitze des Roboterarms bestimmt. So halten wir nur die Elemente, die in die Hände geschickt werden.

Für Ballbilder müssen die Koordinaten noch berechnet werden. Wir werden ein ausgewähltes Objekt zur Kalibrierung verwenden. Wir formulieren die Aufgabe, einen Ball zu finden, neu als "finde die größte rote Region", was auf Python + OpenCV so klingt:

def get_center(image): #       image = cv2.GaussianBlur(image, (7, 7), 0) #     HSV hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV) #    saturation = hsv[...,1] saturation[(hsv[..., 0] > 15) & (hsv[..., 0] < 165)] = 0 _, image1 = cv2.threshold(saturation, 92, 255, cv2.THRESH_BINARY) #     contours = cv2.findContours(image1, cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE)[0] contour = max(contours, key=cv2.contourArea) #    b_circle = cv2.minEnclosingCircle(contour) return b_circle[0]

Schauen wir uns das genauer an.

Nach der Konvertierung in den HSV-Bereich sieht das Bild folgendermaßen aus:

Wie Sie sehen, ist der Farbton bei dunklen Pixeln ziemlich verrauscht, und ein zusätzliches Kriterium für die Segmentierung ist erforderlich. Lass nur die roten Pixel

t e x t h u e [u, v] i n [- 15; 15]

$\ text {hue} [u, v] \ in [-15; 15]$ , und schauen Sie sich den Sättigungskanal an. Auf diesem Kanal fällt die Kalibrierkugel deutlich auf.

Dann sieht das letzte Kriterium so aus:

Überprüfen Sie, ob der Farbton ungefähr rot ist
Belassen Sie nur Pixel mit einer Sättigung über einem bestimmten Schwellenwert
Binarisieren Sie das Bild

Danach bekommen wir so etwas wie folgendes:

Jetzt müssen Sie die Koordinaten des Mittelpunkts der Kugel finden. Es gibt verschiedene Ansätze. Sie können beispielsweise das 3D-Modell der Kugel an eine Punktwolke anpassen. Bei Realsense D435 sind die Tiefenwerte an den Rändern von Objekten jedoch ziemlich verrauscht, sodass wir einen anderen Weg gehen werden.

Wir gehen davon aus, dass der Ball hier die größte zusammenhängende Fläche ist. Dann finden wir seinen Mittelpunkt und ermitteln aus der Tiefe des Kanals die Tiefe bis zu diesem Punkt auf der Oberfläche der Kugel. Und mit ein wenig Hilfe aus der Stereometrie bewegen wir uns vom sichtbaren Punkt auf der Oberfläche des Balls in die Mitte.

Um die Mitte des Balls zu finden, verwenden wir das Wissen, dass die Projektion ein Kreis sein sollte, und wir möchten eine unvoreingenommene Schätzung der Mitte erhalten (aber der Saugnapf des Roboters versucht, uns daran zu hindern). Hier genügt es, einen Kreis mit einer minimalen Fläche zu finden, der diese Fläche beschreibt, und dies wurde bereits in opencv - minEnclosingCircle entschieden .

Nachdem wir die 2 Koordinaten des Punktes u, v in Pixeln und die Tiefe dazu in Millimetern erhalten haben, übersetzen wir sie in physikalische Koordinaten in der Kamera SK:

 def get_world_coords(u, v, depth, camera_matrix): f = np.linalg.inv(camera_matrix) l = np.array([u,v,1]) * depth return np.dot(f,l)

camera_matrix - Matrix der internen Parameter der Kamera gemäß der Formel .

Schritt 4. Führen Sie die Kalibrierung durch

Momentan haben wir 2 Sätze von Punkten für verschiedene Positionen im Raum erhalten: die Koordinaten der Kugeloberseite - der Punkt, für den der Ball den Roboter im SC des Roboters ansaugt, und die Koordinaten des sichtbaren Mittelpunkts des Balls - der Punkt der Kugel, der der Kamera im SC der Kamera am nächsten liegt. Um sie zu vergleichen, müssen Sie sie zuerst an einen physischen Punkt des Balls bringen.

Am einfachsten ist es, diese Punkte in die Mitte des Balls zu verschieben. Wir messen seinen Radius r = 24mm. Dann ist es klar, wie man die Koordinaten des Mittelpunkts der Kugel O vom Tangentialpunkt K erhält - die Berührung ist entlang der Z- Achse immer 1 Radius höher.

Es verbleibt die Übersetzung der Koordinaten des V- Zentrums des sichtbaren Bereichs in die Koordinaten des Mittelpunkts der Kugel O. Verwenden Sie die folgende Abbildung, um die Vorgehensweise zu erläutern:

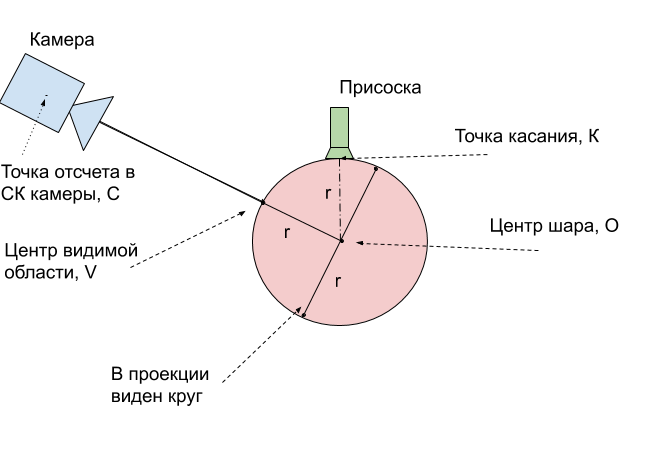
Es zeigt sich, dass der reale Mittelpunkt der Kugel O immer genau 1 Radius tiefer liegt als der sichtbare Punkt V. Dies bedeutet, dass der gefundene Radiusvektor um 24 mm verlängert werden muss.

v e c C O = v e c C V + f r a c v e c C V | v e c C V | r

$\ vec {CO} = \ vec {CV} + \ frac {\ vec {CV}} {| \ vec {CV} |} r$

Bleibt einiges übrig - mit 2 Sätzen von 3D-Koordinaten, die denselben physikalischen Punkten entsprechen, wird die Transformation des ersten Satzes in den zweiten gefunden. Wir werden dafür die Funktion opencv cv2.estimateAffine3D verwenden. Für ideal gefundene Koordinaten ist die affine Transformation natürlich eine Aufzählung, um die Transformation von Punkten zu beschreiben, reichen Rotation und Verschiebung aus, Dehnung wird überflüssig. Durch die Verwendung der affinen Transformation können Sie jedoch Ungenauigkeiten mit einer schlecht berechneten Matrix interner Kameraparameter ausgleichen. Darüber hinaus können Sie eine Kalibrierung durchführen, ohne sie zu kennen.

 transformation = cv2.estimateAffine3D(camera_coords, robot_coords)

Die Ausgabe ist eine 3x4-Transformationsmatrix, die ersten 3x3-Komponenten sind eine Rotationsmatrix, die mit einer Ausdehnung entlang der Achsen kombiniert ist. Mit der richtigen Kamerakalibrierung und guten Eingabedaten sollten Sie eine Matrix in der Nähe der Rotationsmatrix erhalten. Die restlichen 3 Zahlen sind der Verschiebungsvektor zwischen der Kamera und dem Roboter.

Schritt 5. Wir verwenden die Kalibrierung

Um die erhaltene Kalibrierung zu verwenden, müssen die angegebenen Transformationen wiederholt werden. Wir bringen sie in einen einzigen Algorithmus.

Wir finden auf dem RGBD-Bild die Koordinaten des Punktes u, v, die für uns von Interesse sind
Wir übersetzen sie in der Kamera SK in physikalische Koordinaten x, y, z unter Verwendung der Matrix interner Parameter
Im Falle eines Balls liegt der Punkt, der uns interessiert, in der Tiefe des Balls $v '= \ frac {| v | + r} {| v |} \ cdot v, v = [x, y, z]$
Wir wenden die gefundene Transformationstransformation an, die wir mit der Matrix T bezeichnen
$v '' = T \ times [v'_0, v'_1, v'_2, 1] ^ T$
Wir haben die Koordinaten der Ballmitte im SK-Roboter. Damit der Roboter nicht versucht, den Ball zu durchbohren, senden wir zur Kontrolle einen Punkt 1 Radius höher $v '' '= [v' '_ 0, v' '_ 1, v' '_ 2 + r]$

Kalibriergenauigkeit

Wir haben die Kalibrierung an 9 Stellen berechnet. Bei einem Validierungssatz von 6 weiteren Positionen wurde eine Genauigkeit von 2,5 mm mit einem Arbeitsbereich von 16 x 30 x 5 cm erhalten. Dazu haben wir die gefundene Transformation auf die verbleibenden Bilder angewendet und die durchschnittliche Länge des Fehlervektors berechnet.

Schritt 6. Wir verwenden in angewandten Aufgaben

Nachdem Sie die Kalibrierung durchgeführt haben, können Sie anfangen, echte Probleme zu lösen. Zum Beispiel haben wir einen VR-Helm mit Steuerungen verbunden und konnten den Roboter steuern und die Würfel in der virtuellen Realität bewegen.

Diese Kalibrierungsmethode ist jedoch recht allgemein. Es spielt keine Rolle, welche Kamera und welcher Roboter verwendet werden, das beschriebene Verfahren erleichtert die Berechnung der Beziehung zwischen den Koordinatensystemen des Roboters und der Kamera. Darüber hinaus ist das Verfahren bei kleinen Änderungen autonom, so dass der Roboter automatisch eine Kalibrierung durchführen kann, da sich die Kamera mit der Zeit relativ zum Roboter bewegt.

Vasyutka und ZlodeiBaal und ich planen, weiterhin über die Welt der Roboter, VR und des maschinellen Lernens zu sprechen, wenn es interessant ist. Und Kalibrierungsquellen finden Sie in meinem geit .

Fügen Sie dem Roboter Augen hinzu

More articles: