"Cryptosystems Protocols": Diffie - Hellman, El-Gamal, MTI / A (0), STS

Wie die Entwickler der Drei-Durchlauf-Protokolle aus dem vorherigen Abschnitt betrachteten die Autoren der folgenden Algorithmen diese nicht nur als mathematische Konstruktionen, die eine elementare Operation (z. B. Verschlüsselung mit öffentlichen Schlüsseln) ermöglichten, sondern versuchten, ein vollständiges Schlüsselverteilungssystem um ein oder zwei Formeln herum aufzubauen. Einige dieser Konstruktionen, die transformiert wurden, werden bis heute verwendet (z. B. das Diffie-Hellman-Protokoll), andere bleiben nur in der Geschichte der Kryptographie und des Informationsschutzes erhalten.

Später in den neunziger Jahren werden mathematische asymmetrische Grundelemente (Verschlüsselung und elektronische Signatur) und Protokolle getrennt. Diese Grundelemente werden verwendet, was im Abschnitt über asymmetrische Protokolle demonstriert wird.

Diffie-Hellman-Protokoll

Der erste Algorithmus mit öffentlichem Schlüssel wurde von Diffie und Hellman 1976 mit dem Titel "New Directions in Cryptography" vorgeschlagen ( Bailey Whitfield Diffie, Martin Edward Hellman, "New Directions in Cryptography" , [Diffie, Hellman 1976] ). Dieses Protokoll, das auch als Diffie-Hellman-Schema bezeichnet werden kann , hat als erstes die Anforderungen an den Kommunikationskanal verringert, um eine sichere Verbindung herzustellen, ohne zuvor Schlüssel auszutauschen.

Das Protokoll ermöglicht es zwei Parteien, einen gemeinsamen Sitzungsschlüssel mithilfe eines Kommunikationskanals zu erstellen, den ein Angreifer abhören kann, jedoch unter der Annahme, dass dieser den Inhalt von Nachrichten nicht ändern kann.

Lassen $$$p$ - eine große Primzahl $$$g$ - ein primitives Element der Gruppe $$$\ mathbb {Z} _p ^ *$ , $$$y = g ^ x \ bmod p$ und $$$p$ , $$$y$ und $$$g$ im Voraus bekannt. Funktion $$$y = g ^ {x} \ bmod p$ Wir betrachten es als unidirektional, das heißt, eine Funktion mit einem bekannten Wert eines Arguments zu berechnen, ist eine einfache Aufgabe, und ihre Inversion (Finden eines Arguments) mit einem bekannten Wert einer Funktion ist schwierig. (Inverse Funktion $$$x = \ log_g y \ bmod p$ die diskrete Logarithmusfunktion genannt. Es gibt derzeit keine schnellen Möglichkeiten, eine solche Funktion für große einfache zu berechnen $$$p$ .)

Das Austauschprotokoll besteht aus folgenden Aktionen.

1. Alice nimmt einen zufälligen $$$2 \ leq a \ leq p - 1$
   $$$Alice \ to \ left \ {A = g ^ a \ bmod p \ right \} \ to Bob$
2. Bob wählt zufällig $$$2 \ leq b \ leq p-1$
   Bob berechnet den Sitzungsschlüssel $$$K = A ^ b \ bmod p$
   $$$Bob \ to \ left \ {B = g ^ b \ bmod p \ right \} \ to Alice$
3. Alice rechnet nach $$$K = B ^ a \ bmod p$
   

Auf diese Weise wird ein gemeinsamer geheimer Sitzungsschlüssel erstellt $$$K$ . Aufgrund der zufälligen Auswahl der Werte $$$a$ und $$$b$ In einer neuen Sitzung wird ein neuer Sitzungsschlüssel empfangen.

Das Protokoll bietet nur die Generierung neuer Sitzungsschlüssel (Ziel G10). Bei Abwesenheit einer dritten vertrauenswürdigen Partei erfolgt keine Authentifizierung der Parteien (Ziel G1), da aufgrund fehlender Passagen mit Bestätigung des Schlüsselbesitzes keine Schlüsselauthentifizierung erfolgt (Ziel G8). Da das Protokoll jedoch keine langen „Hauptschlüssel“ verwendet, können wir sagen, dass es die Eigenschaft der vollkommenen direkten Geheimhaltung hat (Ziel G9).

Das Protokoll kann nur mit Kommunikationskanälen verwendet werden, in die ein aktiver Kryptoanalytiker nicht eingreifen kann. Andernfalls wird das Protokoll für einen einfachen "Mittelangriff" anfällig.

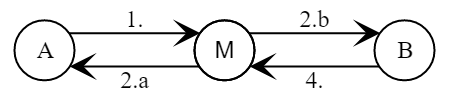
1. Alice nimmt einen zufälligen $$$2 \ leq a \ leq p - 1$
   $$$Alice \ to \ left \ {A = g ^ a \ bmod p \ right \} \ to Mellory ~ (Bob)$
2. Mallory wählt einen zufälligen $$$2 \ leq m \ leq p-1$
   Mallory berechnet mit Alice einen Sitzungsschlüssel für einen Kanal
   

   $$

   $$K_ {AM} = A ^ m \ bmod p = g ^ {am} \ bmod p$$
   
   $$$Mellory ~ (Alice) \ nach \ links \ {M = g ^ m \ bmod p \ nach \} \ nach Bob$
   $$$Mellory ~ (Bob) \ nach \ links \ {M = g ^ m \ bmod p \ nach \} \ nach Alice$
3. Alice berechnet mit Mallory den Sitzungsschlüssel für den Kanal (Mallory ist Bob)
   

   $$

   $$K_ {AM} = M ^ a \ bmod p = g ^ {am} \ bmod p$$
4. Bob wählt zufällig $$$2 \ leq b \ leq p-1$
   Bob berechnet mit Mallory den Sitzungsschlüssel für den Kanal (er denkt, Mallory ist Alice)
   

   $$

   $$K_ {BM} = M ^ b \ bmod p = g ^ {bm} \ bmod p$$
   
   $$$Bob \ to \ left \ {B = g ^ b \ bmod p \ right \} \ to Mellory ~ (Alice)$
5. Mallory berechnet einen Sitzungsschlüssel für einen Kanal mit Bob
   

   $$

   $$K_ {BM} = B ^ m \ bmod p = g ^ {bm} \ bmod p$$
   
   

Infolgedessen erhielten Alice und Bob neue Sitzungsschlüssel, stellten jedoch keinen „sicheren“ Kommunikationskanal untereinander her, sondern einen Angreifer, der nun die Möglichkeit hat, alle zwischen Alice und Bob übertragenen Nachrichten weiterzuleiten oder zu ändern.

Das Diffie-Hellman-Protokoll unterscheidet sich von den meisten Schlüsselverteilungsprotokollen dadurch, dass es keine anderen kryptografischen Grundfunktionen (Verschlüsselung, digitale Signatur oder Hashing-Funktionen) verwendet, sondern in gewisser Weise ein kryptografisches Grundelement für die Erstellung komplexerer Protokolle ist. Es ermöglicht die Erzeugung von Zufallszahlen in einem verteilten System ohne ein vertrauenswürdiges Zentrum. Darüber hinaus kann keine Seite die andere Seite zwingen, den alten Sitzungsschlüssel zu verwenden, im Gegensatz zum Beispiel zum Yahalom-Protokoll.

Das Protokoll kann so geändert werden, dass anstelle der multiplikativen Gruppe der einfachen Multiplikation die additive Gruppe der Addition von Punkten der elliptischen Kurve verwendet wird. In diesem Fall wählen die Parteien immer noch einige zufällige ganze Zahlen aus, erhöhen jedoch nicht die Generatorzahl, sondern multiplizieren den Generatorpunkt mit der gewünschten Zahl.

1. Die Parteien einigten sich auf eine Gruppe von Punkten der elliptischen Kurve $$$\ mathbb {E}$ seine zyklische Untergruppe $$$\ mathbb {G}$ Macht $$$n = \ | \ mathbb {G} \ |$ und Generator $$$G$ Gruppen $$$\ mathbb {G}$ (oder zumindest eine ausreichend große Untergruppe der Gruppe $$$\ mathbb {G}$ )
2. Alice nimmt einen zufälligen $$$2 \ leq a \ leq n - 1$
   $$$Alice \ to \ left \ {A = a \ times G \ right \} \ to Bob$
3. Bob wählt zufällig $$$2 \ leq b \ leq n - 1$
   Bob berechnet den Punkt $$$K = b \ mal A$
   $$$Bob \ to \ left \ {B = g \ times G \ right \} \ to Alice$
4. Alice berechnet den Punkt $$$K = a \ mal B$

Als neuen Sitzungsschlüssel können die Teilnehmer beispielsweise die erste Koordinate des gefundenen Punkts auswählen $$$K$ .

El Gamal-Protokoll

Das El-Gamal-Protokoll ( [ElGamal, 1984] , [ElGamal, 1985] ) sieht aufgrund der vorläufigen Verteilung des öffentlichen Schlüssels einer der Parteien die Authentifizierung des Schlüssels für diese Seite vor. Es kann garantiert werden, dass nur der Besitzer des entsprechenden privaten Schlüssels den Sitzungsschlüssel berechnen kann. Die Bestätigung des Zugangs des Schlüssels (Erfüllung der Ziele G1 und G8) ist jedoch nicht Bestandteil des Protokolls.

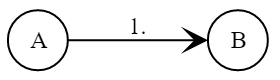
1. Alice und Bob wählen gemeinsame Optionen $$$p$ und $$$g$ wo $$$p$ Ist eine große Primzahl und $$$g$ - primitives Feldelement $$$\ mathbb {Z} _p ^ *$ .
   Bob erstellt ein Paar privater und öffentlicher Schlüssel $$$b$ und $$$K_B$ :
   

   $$

   $$\ begin {array} {l} b: 2 \ leq b \ leq p - 1, \\ K_B = g ^ b \ bmod p. \ end {array}$$
   
   Öffentlicher Schlüssel $$$K_B$ Es ist öffentlich zugänglich für alle Beteiligten. Ein Kryptoanalytiker kann ihn nicht ersetzen - die Substitution wird spürbar.
2. Alice sucht ein Geheimnis $$$x$ und berechnet den Sitzungsschlüssel $$$K$
   

   $$

   $$K = K_B ^ {x} = g ^ {bx} \ bmod p.$$
   
   

   $$

   $$Alice \ to \ left \ {g ^ x \ bmod p \ right \} \ to Bob$$
3. Bob berechnet den Sitzungsschlüssel
   

   $$

   $$K = (g ^ x) ^ {b} = g ^ {bx} \ bmod p.$$

Das Protokoll garantiert nicht die Auswahl eines neuen Sitzungsschlüssels in jeder Protokollsitzung (G10) und die Verwendung eines Hauptschlüssels $$$K_B$ Durch die Übertragung eines Sitzungsschlüssels kann ein Angreifer alle Sitzungsschlüssel aus früheren Sitzungen berechnen, wenn ein privater Schlüssel gefährdet ist $$$b$ (Ziel G9).

MTI / A-Protokoll (0)

1986 schlugen C. Matsumoto ( Tsutomu Matsumoto ), I. Takashima ( Youichi Takashima ) und H. Imai ( Hideki Imai ) mehrere Algorithmen vor, die später als MTI-Protokollfamilie bezeichnet wurden ( [Matsumoto, Tsutomu, Imai 1986] ). Aufgrund der vorläufigen Verteilung der öffentlichen Schlüssel beider Parteien wurde eine implizite Schlüsselauthentifizierung (Ziel G7) bereitgestellt. Das heißt, ein Sitzungsschlüssel kann nur von den Eigentümern der entsprechenden öffentlichen Schlüssel garantiert werden. Wir werden einen der Vertreter dieser Familie betrachten - das MTI / A (0) -Protokoll.

Zuvor waren sich die Parteien über die allgemeinen Systemparameter einig. $$$p$ und $$$g$ wo $$$p$ Ist eine große Primzahl und $$$g$ - primitives Feldelement $$$\ mathbb {Z} _p ^ *$ .


Jede der Parteien (Alice und Bob) erzeugte ein Paar privater und öffentlicher Schlüssel:

$$

$$\ begin {array} {ll} Alice: & ~ a, ~~ K_A = g ^ a \ bmod p, \\ Bob: & ~ b, ~~ K_B = g ^ b \ bmod p. \\ \ end {array}$$

1. Alice generierte eine Zufallszahl $$$R_A: ~ 2 \ leq R_A \ leq p-1$
   $$$Alice \ to \ left \ {g ^ {R_A} \ bmod p \ right \} \ to Bob$
2. Bob erzeugte eine Zufallszahl $$$R_B: ~ 2 \ leq R_B \ leq p-1$
   Bob fand einen Sitzungsschlüssel heraus $$$K = (g ^ {R_A}) ^ b \ cdot K_A ^ {R_B} \ bmod p$
   $$$Bob \ to \ left \ {g ^ {R_B} \ bmod p \ right \} \ to Alice$
3. Alice berechnete den Sitzungsschlüssel $$$K = (g ^ {R_B}) ^ a \ cdot K_B ^ {R_A} \ bmod p$

Wenn die öffentlichen Schlüssel $$$K_A$ und $$$K_B$ stimmen mit Ihren privaten Schlüsseln überein $$$a$ und $$$b$ , dann stimmen die von den Teilnehmern berechneten Sitzungsschlüssel überein:

$$

$$\ begin {array} {ll} (g ^ {R_A}) ^ b \ cdot K_A ^ {R_B} \ bmod p & = & g ^ {b R_A + a R_B} \ bmod p, \\ (g ^ { R_B}) ^ a \ cdot K_B ^ {R_A} \ bmod p & = & g ^ {aR_B + bR_A} \ bmod p. \ end {array}$$

Aufgrund der Komplexität der diskreten Logarithmusaufgabe ist ein Angreifer nicht in der Lage, diese zu erhalten $$$a, R_A$ oder $$$b, R_B$ Aus den übermittelten Nachrichten und der vorläufigen Veröffentlichung von öffentlichen Schlüsseln wird sichergestellt, dass nur legitime Benutzer den Sitzungsschlüssel erhalten. Zufällige Auswahl $$$R_A$ und $$$R_B$ stellt sicher, dass beide Parteien sicher sein können, in jeder Protokollsitzung einen neuen Sitzungsschlüssel zu erstellen.

Wie andere Vertreter der Kryptosystemprotokolle wurde MTI nicht unter Berücksichtigung der Möglichkeit entwickelt, geschlossene "Hauptschlüssel" zu kompromittieren $$$a$ und $$$b$ (Ziel G9).

Station-to-Station-Protokoll

Das STS-Protokoll ( Station-to-Station , [Diffie, Oorschot, Wiener 1992] ) ist für mobile Kommunikationssysteme vorgesehen. Es verwendet die Ideen des Diffie-Hellman-Protokolls und des RSA-Kryptosystems. Ein Merkmal des Protokolls ist die Verwendung eines elektronischen Signaturmechanismus zur gegenseitigen Authentifizierung der Parteien.

Zuvor waren sich die Parteien über die allgemeinen Systemparameter einig. $$$p$ und $$$g$ wo $$$p$ Ist eine große Primzahl und $$$g$ - primitives Feldelement $$$\ mathbb {Z} _p ^ *$ .

Jede Seite $$$A$ und $$$B$ Besitzt ein langfristiges Schlüsselpaar: einen privaten Schlüssel zum Entschlüsseln und Erstellen einer elektronischen Signatur $$$K _ {\ text {public}}$ und öffentlicher Schlüssel zur Verschlüsselung und Signaturprüfung $$$K _ {\ text {public}}$ .

$$

$$\ begin {array} {ll} A: K_ {A, \ text {privat}}, K_ {A, \ text {öffentlich}}: \ forall M: & \ text {Verify} _A (M, S_A (M )) = true, \\ & D_A (E_A (M)) = M, \\ B: K_ {B, \ text {privat}}, K_ {B, \ text {öffentlich}}: \ forall M: & \ text {Verify} _B (M, S_B (M)) = true, \\ & D_B (E_B (M)) = M. \\ \ end {array}$$

Wo $$$\ text {Verify} _A (\ dots)$ Es ist eine Funktion zum Überprüfen der elektronischen Signatur eines öffentlichen Schlüssels $$$K_ {A, \ text {public}}$ und $$$D_A$ - Entschlüsselungsfunktion mit dem privaten Schlüssel $$$K_ {A, \ text {private}}$ .

Das Protokoll besteht aus vier Durchläufen, von denen drei die Übermittlung von Nachrichten beinhalten ( [Cheryomushkin 2009] ).

1. Alice wählt eine Zufallszahl $$$R_A: 2 \ leq R_A \ leq p-1$ .
   $$$Alice \ to \ left \ {A, m_A = g ^ {R_A} \ bmod p \ right \} \ to Bob$
2. Bob wählt eine Zufallszahl $$$R_B: 2 \ leq R_B \ leq p-1$ .
   Bob berechnet den Sitzungsschlüssel $$$K = m_A ^ {R_B} \ bmod p$ .
   $$$Bob \ nach \ links \ {B, A, m_B = g ^ {R_B} \ bmod p, E_K (S_B (m_A, m_B)) \ rechts \} \ nach Alice$
3. Alice berechnet einen Sitzungsschlüssel $$$K = m_B ^ {R_A} \ bmod p$ .
   Alice überprüft die Signatur in der Nachricht $$$E_K (S_B (m_A, m_B))$ .
   $$$Alice \ to \ left \ {A, B, E_K (S_A (m_A, m_B)) \ right \} \ to Bob$
4. Bob überprüft die Signatur in der Nachricht $$$E_K (S_A (m_A, m_B))$ .

Das Protokoll garantiert die Bildung neuer Schlüssel (G10), jedoch keine perfekte direkte Geheimhaltung (G9).

Wie der Lowe-Angriff von 1996 ( [Lowe 1996] ) gezeigt hat, kann ein Protokoll die Authentifizierung von Subjekten (Ziel G1), Schlüsseln (G7) und den Nachweis des Besitzes des Sitzungsschlüssels (G8) nicht garantieren. Obwohl der Angreifer keinen Zugriff auf den neuen Sitzungsschlüssel erhält, wenn das Protokoll nur zur Authentifizierung der Subjekte verwendet wird, kann Alice den Angreifer für Bob halten.

1. Alice wählt eine Zufallszahl $$$R_A: 2 \ leq R_A \ leq p-1$ .
   $$$Alice \ to \ left \ {A, m_A = g ^ {R_A} \ bmod p \ right \} \ to Mellory ~ (Bob)$
   
2. $$$Mellory \ to \ left \ {M, m_A \ right \} \ to Bob$
   
3. Bob wählt eine Zufallszahl $$$R_B: 2 \ leq R_B \ leq p-1$ .
   Bob berechnet den Sitzungsschlüssel $$$K = m_A ^ {R_B} \ bmod p$ .
   $$$Bob \ nach \ links \ {B, M, m_B, E_K (S_B (m_A, m_B)) \ rechts \} \ nach Mellory$
   
4. $$$Mellory ~ (Bob) \ nach \ links \ {B, A, E_K (S_B (m_A, m_B)) \ rechts \} \ nach Alice$
   
5. Alice berechnet einen Sitzungsschlüssel $$$K = m_B ^ {R_A} \ bmod p$ .
   Alice überprüft die Signatur in der Nachricht $$$E_K (S_B (m_A, m_B))$ .
   $$$Alice \ nach \ links \ {A, B, E_K (S_A (m_A, m_B)) \ nach \} \ nach Mellory ~ (Bob)$
   

Nach dem erfolgreichen Abschluss des Protokolls ist Alice zuversichtlich, dass sie mit Bob kommuniziert.

Wie alle anderen „Kryptosystem-Protokolle“ basiert das Station-to-Station-Protokoll auf einer externen Informationsquelle über die öffentlichen Schlüssel der Teilnehmer, ohne die Richtigkeit und Zuverlässigkeit dieser Quelle in Frage zu stellen. Was im Allgemeinen falsch ist. Wenn bei jeder Sitzung des Protokolls Informationen über die Schlüssel von Teilnehmern extern empfangen werden müssen (z. B. wenn es viele Teilnehmer gibt und keine Möglichkeit besteht, sich die Schlüssel aller zu merken), ist der Kanal zum Erhalten öffentlicher Schlüssel das Hauptziel eines aktiven Kryptoanalytikers für die betrachteten Protokolle. Wie Sie sich mit asymmetrischen Kryptographie-Primitiven davor schützen können, erfahren Sie im nächsten Abschnitt.

Literatur

• [Diffie, Hellman 1976] Diffie W., Hellman ME Neue Wege in der Kryptographie // Informationstheorie, IEEE-Transaktionen auf. - 1976. - Nov. - t. 22, Nr. 6. - p. 644-654. - ISSN 0018-9448. - DOI: 10.1109 / TIT.1976.1055638.
• [ElGamal, 1984] El Gamal T. Ein Kryptosystem mit öffentlichem Schlüssel und ein auf diskreten Logarithmen basierendes Signaturschema // Verfahren von CRYPTO 84 zu Fortschritten in der Kryptologie. - Santa Barbara, Kalifornien, USA: Springer-Verlag New York, Inc., 1985. 10-18. - ISBN 0-387-15658-5. - URL: dl.acm.org/citation.cfm?id=19478.19480 .
• [ElGamal, 1985] El Gamal T. Ein Kryptosystem mit öffentlichem Schlüssel und ein Signaturschema basierend auf diskreten Logarithmen // IEEE-Transaktionen zur Informationstheorie. - 1985. - Juli. - t. 31, Nr. 4. - p. 469-472. - DOI: 10.1109 / TIT.1985.1057074.
• [Matsumoto, Tsutomu, Imai 1986] Matsumoto T., Takashima Y., Imai H. Auf der Suche nach intelligenten Vertriebssystemen // Trans. Inst. Electron Kommun. Eng. Jpn. Sekte E. T. 69. Ausgabe 2. - 02.1986. - mit 99-106.
• [Diffie, Oorschot, Wiener 1992] Diffie W., PC Van Oorschot, Wiener MJ Authentication
  und authentifizierter Schlüsselaustausch // Designs, Codes und Kryptografie. - 1992. - Juni. - t. 2, Nr. 2. - p. 107-125. - ISSN 1573-7586. - DOI: 10.1007 / BF00124891.
• [Lowe 1996] Lowe G. Einige neue Angriffe auf Sicherheitsprotokolle // CSFW '96 Ergebnisse des 9. IEEE-Workshops zu Grundlagen der Computersicherheit. - Washington, DC, USA: IEEE Computer Society, 1996. - S. 162.
• [Cheremushkin 2009] Cheremushkin A. V. Kryptographische Protokolle: grundlegende Eigenschaften und Schwachstellen // Applied Discrete Mathematics. - 2009. - Nov. - Ausgabe. 2. - p. 115-150. - URL: cyberleninka.ru/article/n/kriptograficheskieprotokoly-osnovnye-svoystva-i-uyazvimosti.pdf .