Im Vorgriff auf den Start eines neuen Threads im Kurs "Neuronale Netze in Python" haben wir für Sie eine Übersetzung eines interessanten Artikels vorbereitet.
Eines der Hauptprobleme bei der Implementierung der neuen Generation von Quantencomputern liegt in ihrem grundlegendsten Kunden: dem
Qubit . Qubits können mit Objekten in unmittelbarer Nähe interagieren, die
Energie in der Nähe ihrer eigenen
wandernden Photonen (d. H. Unerwünschte elektromagnetische Felder,
Phononen (mechanische Schwingungen einer Quantenvorrichtung) oder Quantendefekte (Unregelmäßigkeiten auf der Chipoberfläche, die während der Herstellungsphase aufgetreten sind) übertragen. das kann den Zustand von Qubits auf eigene Faust unvorhersehbar ändern.
Die Angelegenheit wird durch viele Aufgaben erschwert, die die Werkzeuge zur Steuerung von Qubits einsetzen. Qubits werden nach
klassischen Methoden verarbeitet und gelesen: Analoge Signale in Form von elektromagnetischen Feldern, gekoppelt mit einer physikalischen Platine, in die ein Qubit eingebaut ist, beispielsweise eine supraleitende Mikroschaltung. Unvollkommenheiten in der Steuerelektronik (die zu weißem Rauschen führen), Störungen durch externe Strahlungsquellen und Schwankungen in Digital-Analog-Wandlern führen zu noch größeren stochastischen Fehlern, die den Betrieb von Quantenmikroschaltungen verschlechtern. Diese praktischen Probleme wirken sich auf die Genauigkeit von Berechnungen aus und schränken daher die Anwendung der kommenden Generation von Quantengeräten ein.
Um die Rechenleistung von Quantencomputern zu erhöhen und den Weg für Quantencomputer in großem Maßstab zu ebnen, müssen zunächst physikalische Modelle erstellt werden, die diese experimentellen Probleme genau beschreiben.
In dem im Nature Partner Journal (npj) Quantum Information (https://www.nature.com/npjqi/articles) veröffentlichten Artikel
„Universelle Quantenkontrolle durch tiefgreifendes
Lernen“ haben wir eine neue Struktur der Quantenkontrolle vorgestellt, die mithilfe von tiefgreifendem Lernen erstellt wurde mit Verstärkung, bei der die praktischen Probleme der Optimierung der Quantenkontrolle mit einer einzigen
Verlustfunktion gekapselt werden können. Die betrachtete Struktur liefert eine Verringerung des durchschnittlichen Fehlers des
Quantentors auf zwei Größenordnungen im Vergleich zu stochastischen Standardlösungen mit Gradientenabfall und eine signifikante Verringerung der Torzeit auf die optimalen Werte der Gatesyntheseanaloga. Unsere Ergebnisse eröffnen in naher Zukunft neue Horizonte für Quantenmodellierung, Quantenchemie und Quantenexzellenztests mit Quantengeräten.
Die Innovation dieses Quantensteuerungsparadigmas basiert auf der Entwicklung einer Quantensteuerungsfunktion und einer effektiven Optimierungsmethode, die auf vertieftem Lernen mit Verstärkung basiert. Um eine umfassende Verlustfunktion zu entwickeln, müssen wir zunächst ein physikalisches Modell eines realistischen Quantenkontrollprozesses entwickeln, in dem wir die Größe des Fehlers genau vorhersagen können. Einer der ärgerlichsten Fehler bei der Bewertung der Genauigkeit von Quantencomputern ist die Leckage: Die Menge der Quanteninformationen, die während der Berechnung verloren gehen. Ein solches Leck tritt normalerweise auf, wenn sich der Quantenzustand eines Qubits aufgrund spontaner Emission auf ein höheres Energieniveau oder auf ein niedrigeres ändert. Aufgrund eines Leckfehlers gehen nicht nur nützliche Quanteninformationen verloren, sondern verschlechtern auch die „Quantität“ und reduzieren letztendlich die Leistung eines Quantencomputers auf die Leistung eines Computers mit klassischer Architektur.
Eine übliche Praxis zum genauen Abschätzen verlorener Informationen während einer Quantenberechnung besteht darin, zuerst die gesamte Berechnung zu modellieren. Dies macht jedoch die Schaffung von Quantencomputern in großem Maßstab zunichte, da sie den Vorteil haben, dass sie Berechnungen ausführen können, die für klassische Computer unmöglich sind. Durch die Verbesserung der physikalischen Modellierung können wir mit unserer Common-Loss-Funktion akkumulierte Leckagefehler, Verstöße gegen Regelgrenzbedingungen, Gesamtventilzeit und Ventilgenauigkeit gemeinsam optimieren.
Mit der neuen Verlustmanagementfunktion besteht der nächste Schritt darin, ein effektives Optimierungswerkzeug zu verwenden, um es zu minimieren. Bestehende Optimierungsmethoden reichen nicht aus, um nach hochpräzisen Lösungen zu suchen, mit denen Schwankungen zuverlässig beherrscht werden können. Stattdessen wenden wir eine Methode an, die auf der Methode des vertieften Lernens mit Verstärkung (RL) basiert,
RL - ein vertrauenswürdiger Bereich . Da dieses Verfahren bei allen Testaufgaben eine gute Leistung zeigt, ist es von Natur aus unempfindlich gegen Probenrauschen und kann komplexe Regelungsprobleme mit Hunderten von Millionen von Regelungsparametern optimieren. Ein wesentlicher Unterschied zwischen dieser On-Policy-RL-Methode und den zuvor untersuchten Off-Policy-RL-Methoden besteht darin, dass die Managementrichtlinie unabhängig vom Verlustmanagement dargestellt wird. Auf der anderen Seite verwenden alle RL-Richtlinien, wie z. B.
Q-Learning , ein einziges neuronales Netzwerk, um den Kontrollpfad und die damit verbundene Belohnung darzustellen, wobei die Kontrolltrajektorie die Kontrollsignale bestimmt, die mit den Qubits auf verschiedenen Maßen verknüpft werden sollen, und die damit verbundene Belohnung misst, wie gut der Takt ist Quantenkontrolle.
On-Policy RL ist bekannt für seine Fähigkeit, nicht-lokale Features in Kontrollpfaden zu verwenden. Dies wird kritisch, wenn die Kontrolllandschaft mehrdimensional und mit einer kombinatorisch großen Anzahl nicht-globaler Lösungen gefüllt ist, wie dies häufig bei Quantensystemen der Fall ist.
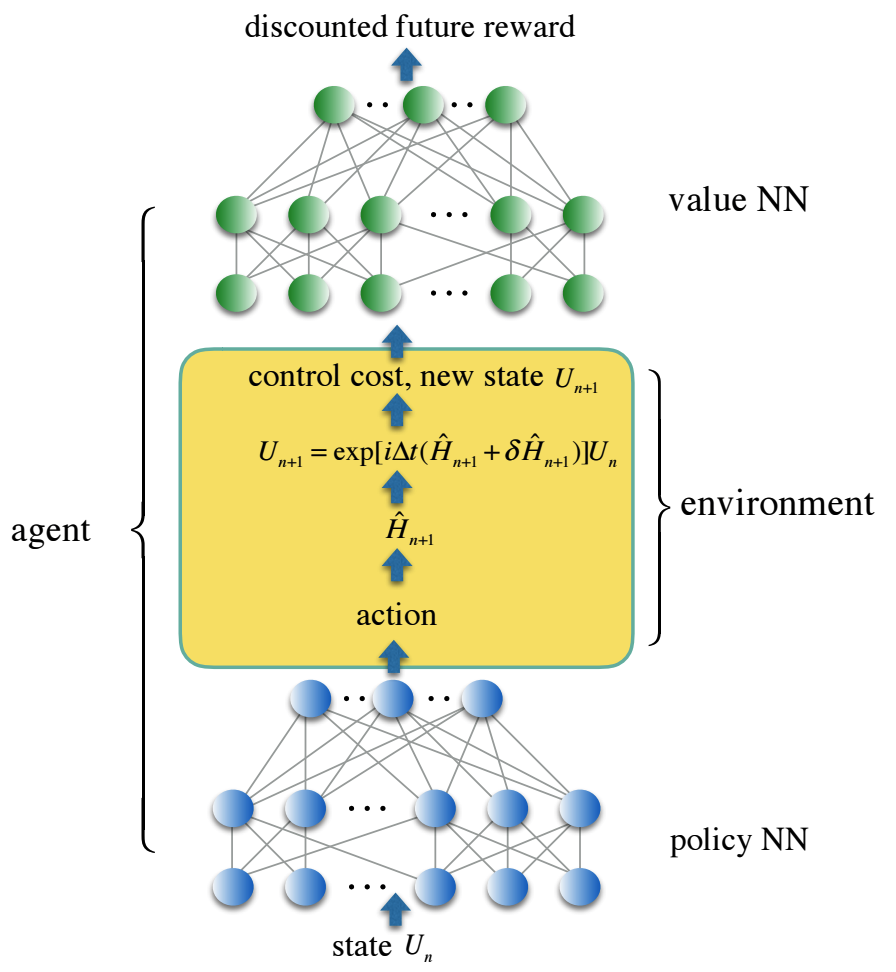
Wir codieren den Steuerpfad in eine dreischichtige, vollständig verbundene NN-Richtlinie für neuronale Netze und die Verluststeuerungsfunktion in den NN-Wert für das zweite neuronale Netz, der den diskontierten zukünftigen Preis widerspiegelt. Zuverlässige Kontrolllösungen wurden mit Verstärkungslernmitteln erhalten, die beide neuronalen Netze in einer stochastischen Umgebung trainieren und eine realistische Geräuschkontrolle simulieren. Wir bieten eine Lösung für die Steuerung einer Reihe von kontinuierlich parametrisierten Zwei-Qubit-Quantengattern an, die für die Anwendung in der Quantenchemie von besonderer Bedeutung sind, aber für die Implementierung mit einer Standard-Universalgattergruppe zu teuer sind.
Im Rahmen dieser neuen Struktur zeigt unsere numerische Simulation eine hundertfache Verringerung der Fehler von Quantentoren und eine Verkürzung der Zeit von Toren für die Familie der kontinuierlich parametrisierten Simulationsquantentore um durchschnittlich eine Größenordnung im Vergleich zu herkömmlichen Ansätzen unter Verwendung eines universellen Satzes von Toren.
Diese Arbeit betont die Wichtigkeit der Verwendung neuer maschineller Lernmethoden und der neuesten Quantenalgorithmen, die die Flexibilität und zusätzliche Verarbeitungsleistung einer universellen Quantensteuerschaltung nutzen. Um das maschinelle Lernen vollständig zu integrieren und die Rechenkapazitäten zu verbessern, müssen zusätzliche Experimente durchgeführt werden, ähnlich wie in dieser Arbeit angegeben.