Die Kategorietheorie ermöglicht es der Mathematik, Gleichheiten aufzugeben

Zwei monumentale Werke überzeugten viele Mathematiker, das Gleichheitszeichen aufzugeben. Ihr Ziel ist es, die Grundlagen der Disziplin mit Hilfe einer schwächeren Beziehung wiederherzustellen - „Äquivalenz“. Und dieser Prozess verläuft nicht immer reibungslos.

Das Gleichheitszeichen ist der Grundstein der Mathematik. Er scheint eine fundamentale und konsistente Aussage zu machen: Diese beiden Einheiten sind genau gleich.

Der Kreis der Mathematiker wächst jedoch, was das Gleichheitszeichen und den anfänglichen Fehler der Mathematik anbelangt. Sie betrachten es als einen externen Glanz, der die wichtigen Schwierigkeiten des Mengenverhältnisses verbirgt - Schwierigkeiten, die Lösungen für eine Vielzahl von Problemen eröffnen können. Sie wollen Mathe mit einer lockereren Äquivalenzsprache reformieren.

"Wir haben diese Idee der Gleichstellung hervorgebracht", sagte Jonathan Campbell von der Duke University. "Und es hätte Äquivalenz an seiner Stelle geben sollen."

Die bekannteste Figur in dieser Gemeinde ist Jacob Lurie . Im Juli trat die 41-jährige Lurie als Vollzeitangestellte in Harvard zurück, um eine Stelle am Princeton Institute for Advanced Studies zu besetzen, an der einige der weltweit führenden Mathematiker arbeiteten.

Ideen in einer Größenordnung wie der von Lurie gibt es auf keinem Gebiet. In seinen Büchern, die Tausende von Seiten voller technischer Details umfassen, hat er einen überraschend anderen Weg gefunden als sonst, um die grundlegendsten Konzepte der Mathematik zu verstehen, der über das Gleichheitszeichen hinausgeht. "Ich denke, es schien ihm, dass dies die richtige Art war, über Mathematik zu denken", sagte Michael Hopkins , ein Harvard-Mathematiker und Leiter der Graduiertenschule.

2009 veröffentlichte er sein erstes Buch, The Theory of Higher Topos . Ein 944-seitiger Band dient als Anleitung zur Interpretation anerkannter Bereiche der Mathematik in der neuen Sprache der "Kategorien der Unendlichkeit". In den folgenden Jahren durchdrangen Luries Ideen ein breites Spektrum mathematischer Disziplinen. Viele Mathematiker halten sie für unverzichtbar für die Zukunft dieses Feldes. "Nach dem Studium der Kategorien der Unendlichkeit wird niemand mehr derselbe sein", sagte John Francis von der Northwestern University.


Jacob Lurie

Die Verbreitung der Kategorien der Unendlichkeit zeigte jedoch alle Probleme, die ein angesehenes Gebiet der Mathematik durchläuft, und versuchte, neue kühne Ideen aufzunehmen - insbesondere eine Idee, die sein wichtigstes Konzept in Frage stellt. "Es gibt ein gewisses Maß an Konservativismus in der mathematischen Gemeinschaft", sagte Clark Barwick von der University of Edinburgh. "Ich glaube nicht, dass von einer Gruppe von Mathematikern erwartet werden kann, dass sie jedes Werkzeug ohne überzeugende Gründe schnell akzeptiert."

Obwohl viele Mathematiker die Kategorien der Unendlichkeit akzeptiert haben, haben nur wenige die gesamten langwierigen und extrem abstrakten Texte von Lurie gelesen. Infolgedessen fällt ein Teil der Arbeit, die auf seinen Ideen basiert, weniger streng aus, als in der Mathematik akzeptiert wird.

"Ich hörte Leute sagen: 'Lurie hat es irgendwo", sagte Inna Zakharevich , Mathematikerin an der Cornell University. - Und ich sage: 'Wirklich? Sie beziehen sich auf 8.000 Textseiten. ' Dies ist kein Hinweis, sondern ein Aufruf an die Behörde. “

Mathematiker versuchen immer noch, sowohl die Breite von Luries Ideen als auch die einzigartige Art, sie zu präsentieren, zu realisieren. Sie extrahieren das Wesentliche seiner Darstellung der Kategorien der Unendlichkeit und präsentieren es in einem neuen Paket, damit mehr Mathematiker es verwenden können. In gewissem Sinne führen sie die notwendige Führung aus, die verpflichtet ist, jeder Revolution zu folgen, indem sie den revolutionären Text in den alltäglichen Gesetzeskodex übersetzen. So schaffen sie die Zukunft der Mathematiker, die nicht auf Gleichheit, sondern auf Gleichwertigkeit basiert.

Endlose Äquivalenztürme

Die mathematische Gleichheit scheint die am wenigsten umstrittene aller Ideen zu sein. Zwei Perlen plus eine Perle entsprechen drei Perlen. Worüber gibt es sonst noch zu reden? Die einfachsten Ideen können jedoch am meisten täuschen.

Seit dem Ende des 19. Jahrhunderts wurden die Grundlagen der Mathematik auf Mengen von Objekten aufgebaut, die als Mengen bezeichnet werden. Die Mengenlehre legt die Regeln oder das Axiom für die Erstellung und Behandlung dieser Mengen fest. Eines dieser Axiome besagt beispielsweise, dass Sie einer Gruppe von zwei Elementen eine Gruppe von einem Element hinzufügen und eine neue Gruppe von drei Elementen erhalten können: 2 + 1 = 3.

Der formale Weg, die Gleichheit zweier Größen zu demonstrieren, besteht darin, Paare miteinander abzugleichen. Ordne eine Perle rechts vom Gleichheitszeichen einer Perle links zu. Nach all den Vergleichen bleiben keine zusätzlichen Perlen übrig.

Die Mengenlehre erkennt an, dass zwei Mengen von jeweils drei Objekten genau aufeinander abgestimmt werden können, meint jedoch nicht alle unterschiedlichen Möglichkeiten eines solchen Vergleichs. Die erste Perle rechts kann ein Paar in Form der ersten Perle links aufnehmen oder die erste rechts mit der zweiten links abgleichen usw. (es können sechs solcher Paare vorhanden sein). Zu sagen, dass zwei plus eins gleich drei sind und damit zu Ende gehen, bedeutet, nicht alle möglichen Möglichkeiten zu sehen, um sie gleichzusetzen. "Das Problem ist, dass es viele Möglichkeiten gibt, sich zu paaren", sagt Campbell. "Und wir vergessen sie, wenn wir gleich sagen."



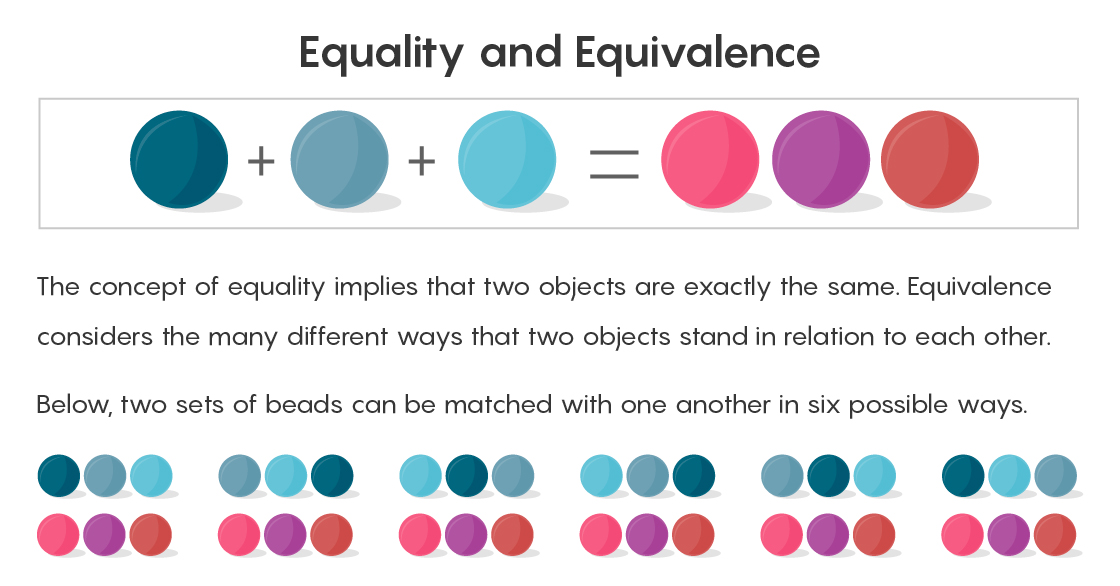
Hier kommt die Äquivalenz ins Spiel. Wenn Gleichheit eine klare Beziehung ist - zwei Dinge sind entweder gleich oder nicht -, kann Gleichheit unterschiedlich sein.

Wenn Sie jedes Element eines Satzes genau mit jedem Element eines anderen Satzes abgleichen, erhalten Sie eine starke Äquivalenz. In einem Gebiet der Mathematik wie der Homotopie sind jedoch zwei Formen (oder geometrische Figuren) gleichwertig, wenn eine durch Strecken oder Komprimieren in eine andere umgewandelt werden kann, ohne zu brechen.

Aus Sicht der Homotopietheorie sind eine flache Scheibe und ein Raumpunkt gleichwertig - die Scheibe kann auf einen Punkt komprimiert werden. Sie können die Punkte auf einer Festplatte jedoch nicht mit den Punkten auf einem Punkt abgleichen. In der Tat hat die Punktscheibe eine unendliche Zahl, und ein Punkt ist nur ein Punkt.



Seit der Mitte des 20. Jahrhunderts haben Mathematiker versucht, eine Alternative zur Mengenlehre zu entwickeln, mit der sich die Mathematik in Bezug auf die Äquivalenz leichter auseinandersetzen lässt. Die Mathematiker Samuel Eileberg und Saunders MacLane führten 1945 ein neues grundlegendes Objekt mit eingebauter Äquivalenz ein. Sie nannten es eine Kategorie.

Eine Kategorie kann mit allem gefüllt werden. Sie können die Kategorie der Säugetiere einnehmen, zu der alle haarigen Warmblüter gehören, die Milch produzieren. Sie können auch Kategorien von mathematischen Objekten erstellen: Mengen, geometrische Formen oder numerische Systeme.

Eine Kategorie ist eine Gruppe mit zusätzlichen Metadaten: eine Beschreibung aller Arten der Zuordnung eines Objekts zu einem anderen, einschließlich einer Beschreibung aller Funktionen, mit denen zwei Objekte als gleichwertig betrachtet werden können. Kategorien können auch als geometrische Objekte betrachtet werden, bei denen jedes Element der Kategorie durch einen Punkt dargestellt wird.

Stellen Sie sich zum Beispiel die Oberfläche einer Kugel vor. Jeder Punkt auf dieser Oberfläche kann die Art der Dreiecke anzeigen. Pfade zwischen Punkten drücken eine Äquivalenzbeziehung zwischen Objekten aus. Aus Sicht der Kategorietheorie vergessen wir die spezifische Art der Beschreibung eines Objekts und konzentrieren uns stattdessen darauf, welchen Platz das Objekt in Bezug auf alle anderen Objekte dieses Typs einnimmt.


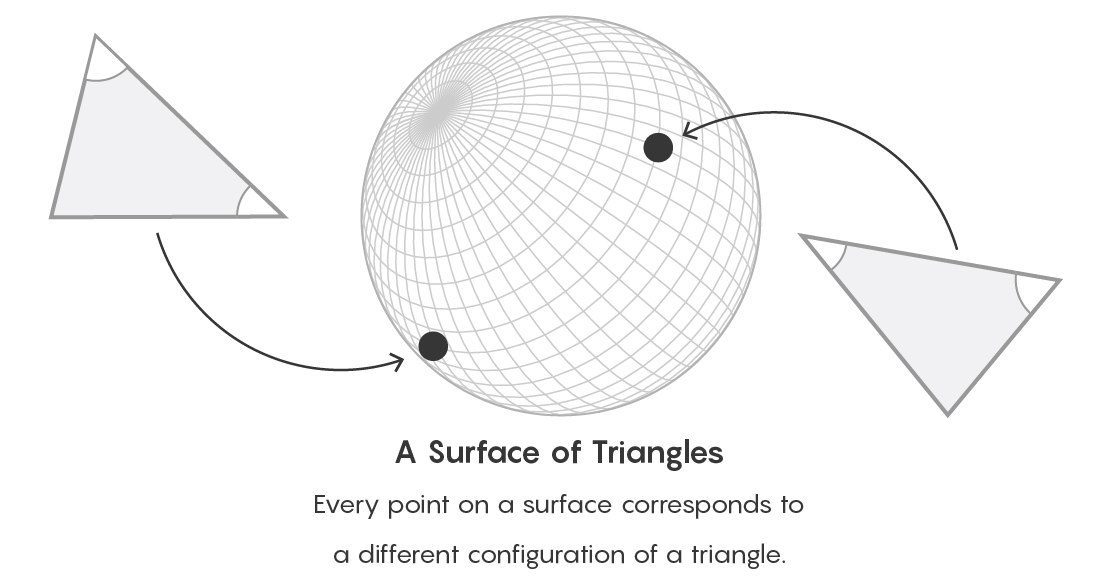Jeder Punkt auf der Oberfläche entspricht einer bestimmten Art von Dreiecken.

"Wir behandeln viele Dinge als Dinge, obwohl sie in Wirklichkeit eine Beziehung zwischen den Dingen sind", sagte Zakharevich. - Der Ausdruck „mein Ehemann“ bedeutet etwas, das wir als Objekt betrachten, aber Sie können sich das als Beziehung vorstellen. Ein gewisser Teil davon wird durch die Beziehung zu mir bestimmt. “

Die Kategorie-Version von Eilenberg und MacLane war gut geeignet, um mit starken Äquivalenzoptionen zu arbeiten. In der zweiten Hälfte des 20. Jahrhunderts verwendeten Mathematiker jedoch zunehmend schwächere Äquivalenzformen wie die Homotopie. "Die Mathematik wird subtiler, und wir haben unweigerlich den Wunsch nach subtileren Vorstellungen über gewöhnliche Dinge", sagte Emily Riel, Mathematikerin an der Johns Hopkins University. In diesen feineren Versionen der Äquivalenz nimmt die Informationsmenge über die Beziehung zwischen zwei Objekten stark zu. Die rudimentären Kategorien von Eilenberg und MacLane waren dafür nicht vorgesehen.

Um mehr Informationen zu erhalten, müssen Sie sich zunächst an unsere Kugel erinnern, die verschiedene Dreiecke kennzeichnet. Zwei Dreiecke sind homotopisch äquivalent, wenn sich eines durch Strecken oder eine andere Verformung in ein anderes verwandeln lässt. Zwei Punkte auf einer Oberfläche sind homotopisch äquivalent, wenn sie durch einen Pfad verbunden sind. Indem Sie die homotopischen Pfade zwischen Punkten auf einer Oberfläche untersuchen, untersuchen Sie tatsächlich die verschiedenen Arten, wie die durch diese Punkte gekennzeichneten Dreiecke miteinander verbunden werden.



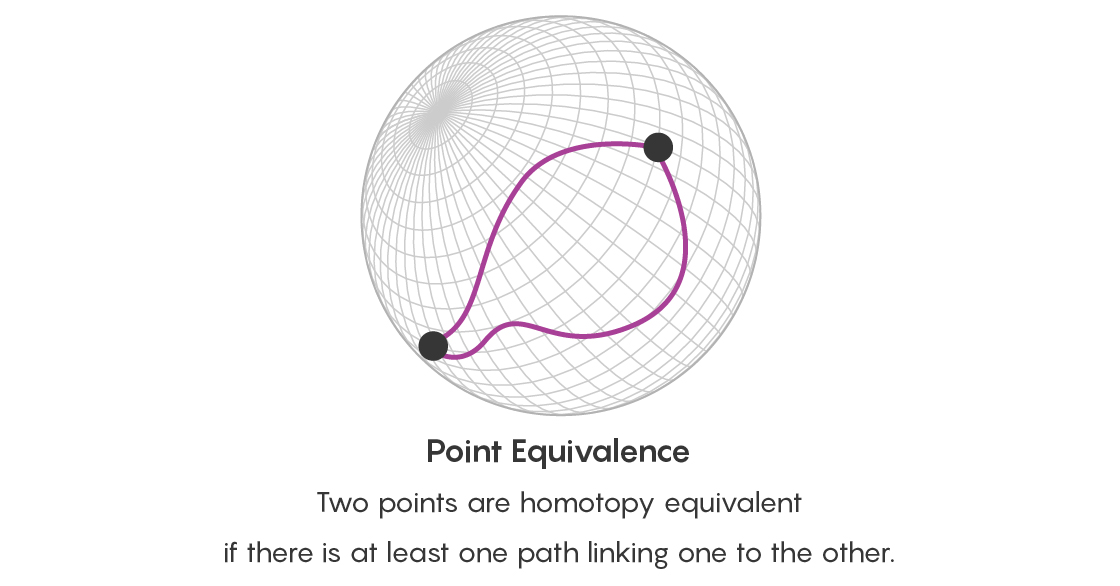
Es reicht jedoch nicht aus, zwei Punkte auf viele gleichwertige Arten miteinander zu verbinden. Es ist auch notwendig, über die Gleichwertigkeit all dieser Pfade nachzudenken. Daher stellen Sie sich zusätzlich zur Frage der Gleichwertigkeit von Punkten die Frage der Gleichwertigkeit von zwei Pfaden, die an denselben Punkten beginnen und enden - und gibt es einen Pfad, der diese Pfade verbindet? Dieser Pfad, der die Pfade verbindet, hat die Form einer Platte, deren Grenze zwei dieser Pfade sind.



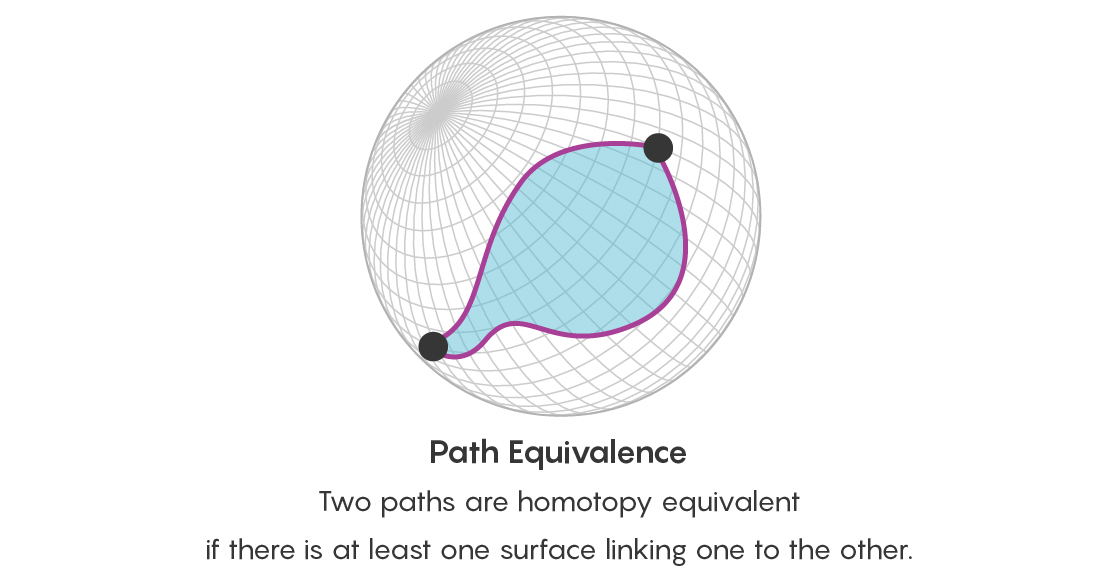
Sie können diese Idee weiterentwickeln. Zwei Festplatten sind äquivalent, wenn sie durch einen Pfad verbunden sind - und dieser Pfad hat die Form eines dreidimensionalen Objekts. Solche dreidimensionalen Objekte können selbst durch vierdimensionale Pfade verbunden sein (der Pfad zwischen zwei Objekten hat immer eine Dimension mehr als die Objekte selbst).

Als Ergebnis bauen Sie einen endlosen Turm der Äquivalenz zwischen Äquivalenzen. Wenn Sie sich über die gesamte Lehre streiten, erhalten Sie einen Überblick über alle Objekte, die Sie mit Punkten auf der Kugel markiert haben.

"Es ist nur eine Kugel, aber um die Form einer Kugel zu verstehen, muss man auf irgendeine Weise ins Unendliche gehen", sagte David Ben-Zvi von der University of Texas in Austin.

In den letzten Jahrzehnten des 20. Jahrhunderts haben viele Mathematiker an der Theorie der „Kategorien von Unendlichkeiten“ gearbeitet - an der Frage, was in der Lage ist, einen unendlichen Turm von Äquivalenzen zwischen Äquivalenzen zu verfolgen. Einige von ihnen haben ernsthafte Erfolge erzielt. Aber nur einer hat das Ende erreicht.

Mathe umschreiben

Die erste Arbeit von Jacob Lurie in den Kategorien der Unendlichkeit war nicht sehr erfolgreich. Am 5. Juni 2003 veröffentlichte der 25-jährige Wissenschaftler ein 60-seitiges Dokument mit dem Titel " On the Topos of Infinity " auf der Website von science preprints arxiv.org. Dort begann er, grobe Entwürfe der Regeln anzufertigen, nach denen Mathematiker mit Kategorien der Unendlichkeit arbeiten konnten.

Nicht jeder akzeptierte die erste Arbeit auf die gleiche Weise. Kurz nach der Lektüre schrieb Peter May , Mathematiker an der Universität von Chicago, an Luries Vorgesetzten Michael Hopkins, dass Luries Arbeit zwar interessante Ideen enthält, aber unvollendet aussieht und einen disziplinierteren Ansatz erfordert.

„Ich habe Mike unsere Kommentare erklärt und er hat sie an Jacob weitergeleitet“, sagte May.

Es ist nicht bekannt, ob Lurie den Brief von May als Herausforderung annahm oder ob er bereits seinen nächsten Schritt geplant hatte (Lurie lehnte zahlreiche Anfragen für ein Interview ab). Es ist klar, dass Lurie nach kritischen Kommentaren eine mehrjährige Produktivitätsperiode erlebte, die später legendär wurde.

"Ich kann nicht in Jacobs Gehirn gelangen und daher weiß ich nicht genau, was er damals gedacht hat", sagte May. "Aber es gibt einen großen Unterschied zwischen dem Entwurf, den wir überprüft haben, und den endgültigen Versionen, die sich bereits auf einer völlig anderen mathematischen Ebene befinden."

Im Jahr 2006 veröffentlichte Lurie auf arxiv.org einen Entwurf von „Theories of Highest Topos“. In diesem monumentalen Werk schuf er den notwendigen Apparat, um die Mengenlehre durch eine neue Grundlage für die Mathematik zu ersetzen, die auf den Kategorien der Unendlichkeit basiert. "Er hat buchstäblich Tausende von Seiten dieses grundlegenden Apparats erstellt, den wir heute alle verwenden", sagte Charles Rezk, Mathematiker an der Universität von Illinois in Urbana-Champaign, der schon früh wichtige Arbeit bei der Entwicklung von Unendlichkeitskategorien geleistet hat. "Ich kann mir nicht vorstellen, wie es möglich ist, ein Werk wie" Theory of the Highest Topos "in einem Leben zu schaffen - und er hat es in zwei oder drei Jahren geschaffen."

Dann gab Lurie 2011 eine weitere, noch längere Arbeit. Darin erfand er die Algebra neu.

Die Algebra gibt uns wunderbare formale Regeln für die Manipulation von Gleichungen. Mathematiker wenden diese Regeln ständig an, um Theoreme zu beweisen. Die Algebra turnt jedoch an den festen Stäben des Gleichheitszeichens. Entfernen Sie diese Balken, und ersetzen Sie sie durch ein kurzlebigeres Äquivalenzkonzept. Einige Vorgänge werden dann sehr kompliziert.

Nehmen Sie eine der ersten Algebra-Regeln, die Kinder in der Schule lernen: Assoziativität. Die Summe oder das Produkt von drei oder mehr Zahlen hängt nicht von ihrer Gruppierung ab: 2 × (3 × 4) = (2 × 3) × 4.

Es ist einfach, die Assoziativitätseigenschaft für eine Liste mit drei oder mehr Zahlen zu beweisen, wenn Sie mit Gleichheit arbeiten. Dies ist schwierig, wenn Sie auch mit dem Konzept der starken Äquivalenz arbeiten. Wenn Sie sich jedoch subtileren Versionen der Äquivalenz zuwenden, mit ihren endlosen Türmen von Pfaden, die die Pfade verbinden, verwandelt sich selbst eine einfache Regel, ähnlich der Assoziativität, in einen dunklen Wald.


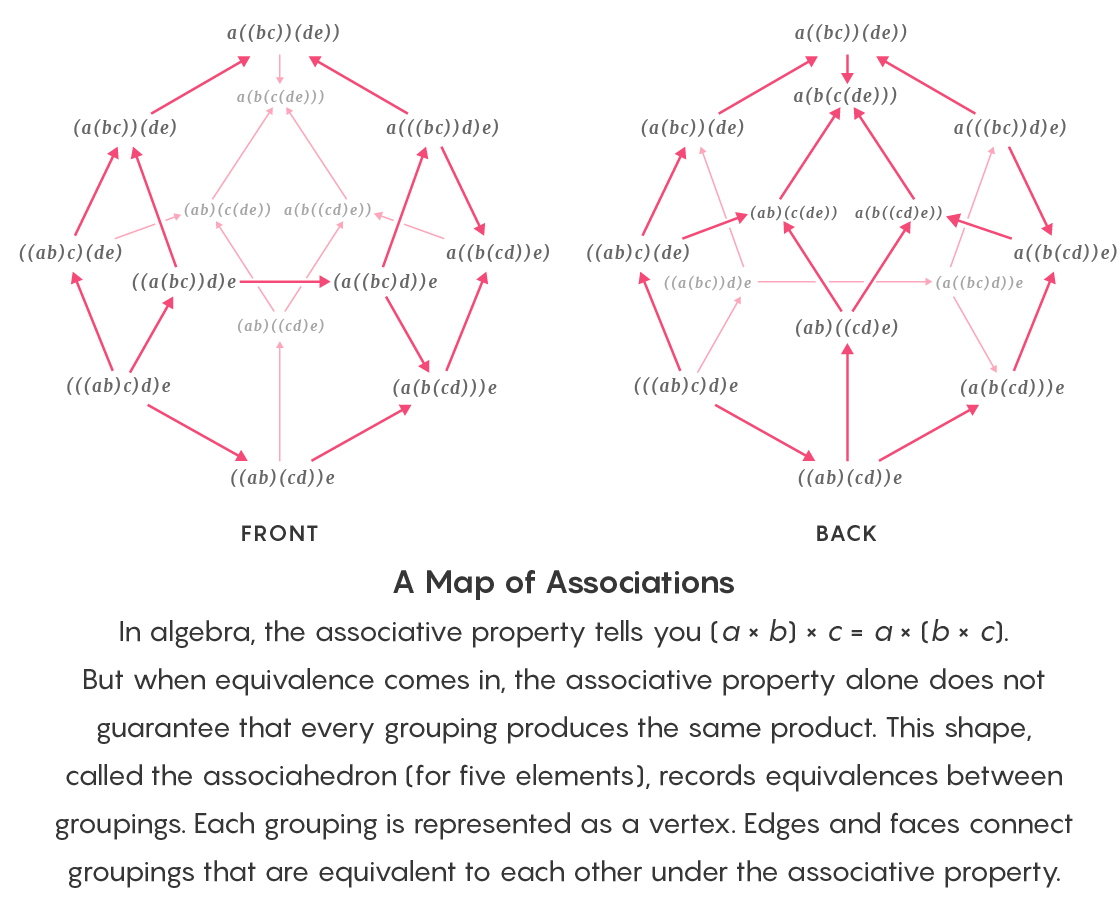In der Algebra besagt die Assoziativität, dass (a × b) × c = a × (b × c). Bei Verwendung der Äquivalenz garantiert die Assoziativität allein jedoch nicht, dass eine Gruppierung von Elementen dasselbe Multiplikationsergebnis liefert. Dieses Assokaeder enthält Gruppenäquivalenzaufzeichnungen. Jeder Eckpunkt entspricht einer Gruppierung. Kanten und Flächen kombinieren Gruppen, die assoziativ gleichwertig sind.

"Dies macht das Problem extrem kompliziert, was es unmöglich macht, mit dieser neuen Version der Mathematik zu arbeiten", sagte David Isla, Mathematiker an der Universität von Montana.

In der Higher Algebra, deren neueste Version mehr als 1553 Seiten umfasst, entwickelte Lurie eine Assoziativitätsoption für Unendlichkeitskategorien sowie viele andere algebraische Theoreme, die zusammen die Grundlage der Äquivalenzmathematik bilden.

Diese beiden Bücher erzeugten den Effekt einer explodierenden Bombe; solche Werke führen zu einer wissenschaftlichen Revolution. "Die Skala war außergewöhnlich", sagte Reel. "Es war das Erreichen des Grothendieck- Niveaus in der algebraischen Geometrie."

Revolution braucht jedoch Zeit, und wie Mathematiker nach der Veröffentlichung von Luries Büchern entdeckten, können diese Jahre chaotisch sein.

Eine Kuh verdauen

Mathematiker gelten als Menschen mit eindeutigem Denken: Der Beweis ist entweder wahr oder nicht; Die Idee funktioniert entweder oder nicht. Mathematiker sind aber auch normale Menschen und reagieren auf neue Ideen wie normale Menschen: subjektiv, emotional, mit persönlichen Motiven.

"Ich denke, dass viele Texte über Mathematiker in einem solchen Ton geschrieben wurden, dass sie nach einer funkelnden, kristallklaren Wahrheit suchen", sagte Campbell. "Aber das passiert nicht." Dies sind Menschen mit ihrem eigenen Geschmack, Komfortzonen und sie können Dinge ablehnen, die sie aus ästhetischen oder persönlichen Gründen nicht mögen. "

In dieser Hinsicht ist die Arbeit von Lurie zu einer komplexen Herausforderung für die Gemeinschaft geworden. In der Tat war es provokativ: Hier ist ein neuer und besserer Weg, Mathe zu machen. Diese Botschaft richtete sich insbesondere an Mathematiker, die ihre gesamte Karriere damit verbracht haben, Methoden zu entwickeln, die Lurie überragte.

"Die Leute wollen nicht immer, dass die nächste Generation ihre Arbeit umschreibt, und dieser Prozess erzeugt Stress", sagte Francis. "Dies ist eines der Merkmale der Theorie der Kategorien der Unendlichkeit - die meisten früheren Arbeiten entsprechen."

Luries Arbeit war aus anderen Gründen schwer zu verdauen. Das Materialvolumen bedeutete, dass Mathematiker Jahre damit verbringen mussten, seine Bücher zu lesen. Es ist fast unmöglich, von vielbeschäftigten Mathematikern, die sich mitten in einer Karriere befinden, ein Ergebnis zu fordern. Für Doktoranden, die nur wenige Jahre Zeit haben, um einen Job zu finden, ist dies sehr riskant.

Luries Arbeit war auch sehr abstrakt, selbst im Vergleich zu der extrem abstrakten Natur aller fortgeschrittenen Mathematikstudien. Und nicht allen hat es gefallen. "Viele Leute dachten, Luries Arbeit sei abstrakter Müll und viele verliebten sich einfach in sie", sagte Campbell. "Es gab Zwischenoptionen, einschließlich derer, die sie überhaupt nicht verstanden haben."


Emily rollen

Die wissenschaftliche Gemeinschaft nimmt ständig neue Ideen wahr, aber normalerweise geschieht dies langsam und mit dem Gefühl, dass sich alle gleichzeitig bewegen. Die Entstehung neuer Ideen schafft Schwierigkeiten für den intellektuellen Apparat der Gemeinschaft. "Viele neue Dinge tauchen sofort auf - es ist wie eine Boa, die versucht, eine Kuh zu verdauen", sagte Campbell. "Eine riesige Masse zieht durch die Gemeinde."

Wenn Sie ein Mathematiker sind, der glaubt, dass Luries Ansatz der beste Weg ist, um Mathematik zu üben, dann ist Ihr Weg nach vorne einsam. Wenige Leute lasen Luries Arbeit, es gab keine Lehrbücher, in denen sie kurz beschrieben werden konnten, und keine Seminare, die Ihnen dabei halfen, sich zurechtzufinden. "Es gab nur einen Weg, dies alles im Detail zu studieren - sich hinzusetzen und alles selbst zu tun", sagte Peter Heine, ein Doktorand am MIT, der ein Jahr lang Luries Arbeit las. - Ich denke, das ist das Schwierigste. "Es ist nicht einfach, sich hinzusetzen und es selbst herauszufinden - nämlich sich hinzusetzen und 800 Seiten der Theorie der Topos-Theorie selbst zu lesen.

Wie bei vielen neuen Erfindungen erfordert die Theorie der höheren Topos, dass Mathematiker aktiv mit dem Apparat interagieren, damit dieser funktionieren kann. 16- , , . « , », — , , .

, . . : ?

« , , , , — . – , , , ».

, , , – .

. , . , – , , , - , .

« , — , , . – , , , , – , , - , . , ».

. , , .

« », — .

, , . , , , . , , .

« ' , , ', — . – , ' , , '».

, .

, , . , – , , , . .

. . , , . « , , », — .

, . , , , .

. , , ( ) . « , , , : , , — . – ».

. , , , , . , , , « » . : « , , — . – ».

. , . , , , , , , , « ».

« , , — . – , ».

. Kerodon , , . , « » , – .

« , , — . – – , - ».