Auf den Spuren von
„Unser Won: TopCoder Open 2019“ veröffentliche ich Aufgaben aus dem Algorithmus-Track
(klassische Sportprogrammierung. In anderthalb Stunden müssen Sie drei Probleme in Java, C #, C ++ oder Python lösen.)1. Kuchen für sechs
Erklärung des ProblemsDas Zeitlimit beträgt 4 Sekunden.
Du hast einen Kuchen. Von oben gesehen hat der Kuchen die Form eines (streng) konvexen Polygons. Sie erhalten die Koordinaten der Eckpunkte in ganzen Zahlen X und Y.
Du hast fünf Freunde. Sie möchten den Kuchen in sechs Stücke gleicher Fläche (aber nicht unbedingt gleicher Form) teilen. Natürlich kann es jeder in fünf Schnitten machen, aber nur die Profis können es in drei Schnitten machen.
Suchen Sie drei Schnitte in geraden Linien durch einen Punkt, der den Kuchen in sechs gleich große Stücke teilt. Drucken Sie {x, y, d1, d2, d3}, wobei (x, y) der gemeinsame Punkt aller drei Abschnitte ist und d1, d2, d3 die Richtungswinkel der Abschnitte im Bogenmaß sind.
DefinitionKlasse: CakeForSix
Methode: schneiden
Parameter: int [], int []
Rückgabe: double []
Methodensignatur: double [] cut (int [] x, int [] y)
(Stellen Sie sicher, dass Ihre Methode öffentlich ist.)
Hinweise- Die positive Richtung entlang der x-Achse ist 0 (Bogenmaß), die positive Richtung entlang der y-Achse ist pi / 2 (Bogenmaß).
- Der Schnitt in Richtung d ist ähnlich dem Schnitt in Richtung pi * k + d für eine beliebige ganze Zahl k.
- Sie können beliebige Richtungen ausgeben, sie müssen nicht von [0, pi) stammen.
- Der Sortierer berechnet die Fläche Ihrer sechs Kuchenstücke im Doppel. Die Antwort wird akzeptiert, wenn der relative oder absolute Unterschied zwischen ihnen weniger als 10 ^ (- 4) beträgt.
- Genauer gesagt, lassen Sie X und Y die kleinste und größte Ihrer sechs vom Grader berechneten Flächen sein. Dann wird Ihre Antwort akzeptiert, wenn Y <max (X + 10 ^ (- 4), X * 1 + 10 ^ (- 4)).
- (In der ursprünglichen Version des Problems wurde die Genauigkeit 1e-7 anstelle von 1e-4 verwendet. Um dieses Problem im Archiv zu beheben, wurde die Genauigkeitsbeschränkung reduziert, da Aufruffälle vorhanden waren, die die Aufgabe höchstwahrscheinlich mit der Genauigkeit 1e-7 unlösbar machen. In einer idealen Welt gelten Einschränkungen Lassen Sie solche Fälle nicht zu und erfordern Sie dennoch eine hohe Genauigkeit. Daher ist es nicht einfach, das Problem mit einer allgemeinen numerischen Optimierung zu lösen.)
Einschränkungen- x enthält 3 bis einschließlich 50 Elemente.
- y enthält so viele Elemente wie x.
- alle Koordinaten zwischen 0 und 10.000 inklusive
- x und y definieren ein konvexes Polygon gegen den Uhrzeigersinn.
Original in EnglischProblemstellung
Das Zeitlimit beträgt 4 Sekunden.
Du hast einen Kuchen. Von oben gesehen ist der Kuchen ein (streng) konvexes Polygon. Sie erhalten die Koordinaten seiner Eckpunkte in int [] sx und y.
Du hast fünf Freunde. Sie möchten nun den Kuchen in sechs Stücke von gleicher Fläche (aber nicht unbedingt gleicher Form) schneiden. Natürlich kann jeder das in fünf Schnitten machen - aber nur ein echter Profi kann es in drei!
Finden Sie drei gerade Schnitte, die durch denselben Punkt verlaufen, der den Kuchen in sechs gleich große Teile schneidet. Geben Sie {x, y, d1, d2, d3} zurück, wobei (x, y) der gemeinsame Punkt der drei Schnitte ist und d1, d2, d3 ihre Richtungen im Bogenmaß sind.
Definition
Klasse: CakeForSix
Methode: schneiden
Parameter: int [], int []
Rückgabe: double []
Methodensignatur: double [] cut (int [] x, int [] y)
(Stellen Sie sicher, dass Ihre Methode öffentlich ist.)
Hinweise
- Die positive Richtung entlang der x-Achse ist 0 (Bogenmaß), die positive Richtung entlang der y-Achse ist pi / 2 (Bogenmaß).
- Ein Schnitt in Richtung d entspricht einem Schnitt in Richtung pi * k + d für eine beliebige ganze Zahl k.
- Sie können alle Richtungen zurückgeben, sie müssen nicht aus [0, pi) stammen.
- Der Sortierer berechnet die Flächen Ihrer sechs Kuchenstücke doppelt. Die Antwort wird akzeptiert, wenn der relative oder absolute Unterschied zwischen ihnen weniger als 10 ^ (- 4) beträgt.
- Genauer gesagt, lassen Sie X und Y die kleinste und die größte Ihrer sechs Flächen sein, wie sie vom Grader berechnet wurden. Dann wird Ihre Antwort akzeptiert, wenn Y <max (X + 10 ^ (- 4), X * (1 + 10 ^ (- 4)).
- (In der Originalversion des Problems wurde 1e-7-Genauigkeit anstelle von 1e-4 verwendet. Zur Behebung dieses Problems im Archiv wurde die Genauigkeitsbeschränkung herabgesetzt, da es Herausforderungsfälle gab, die die Aufgabe höchstwahrscheinlich mit 1e-7-Genauigkeit unlösbar machen In einer idealen Welt würden die Einschränkungen solche Fälle nicht zulassen und erfordern dennoch eine hohe Präzision, so dass es nicht einfach ist, das Problem durch eine allgemeine numerische Optimierung zu lösen.)
Einschränkungen
- x enthält zwischen 3 und 50 Elemente.
- y hat die gleiche Anzahl von Elementen wie x.
- Alle Koordinaten liegen zwischen 0 und 10.000 einschließlich.
- x und y beschreiben ein konvexes Polygon gegen den Uhrzeigersinn.
Beispiele
0){0, 20, 30, 50, 30, 20}
{10, 0, 0, 10, 20, 20}
Rückgabe:
{24.999999999437453, 9.999999999500002, 0.0, 0.7266423406817211, 2.4149503129080787}
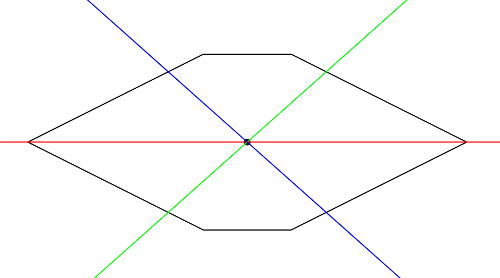
Symmetrisches aber nicht regelmäßiges Sechseck. Ein Beispiel für eine Antwort besteht darin, sie horizontal zu halbieren und in der Mitte zwei weitere Schnitte auszuführen, die jeden Teil in drei Teile unterteilen.
 1)
1){0, 1000, 0}
{0, 0, 1000}
Rückgabe:
{333.3333333331763, 333.3333333332546, 0.7853981633986264, 2.0344439357948154, 2.6779450445891753}
Rechtwinkliges Dreieck Wir können wieder mit einem von drei Schnitten entlang der Symmetrieachse beginnen.
 2)
2){40, 70, 90, 90, 50}
{30, 20, 40, 100, 60}
Rückgabe:
{69.79517771922892, 52.77575974637605, 2.0616329654335885, 3.637826104091601, 4.32123485812475}
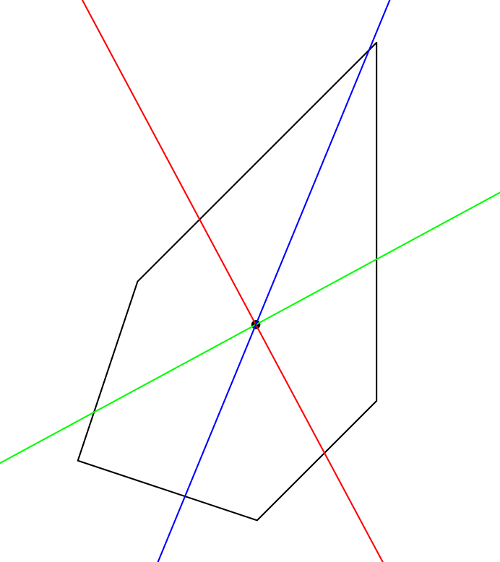
Falsches Fünfeck.
 3)
3){300, 400, 300, 200}
{500, 600, 700, 600}
Rückgabe: {299.99999999974995, 599.9999999995, 0.0, 1.107148717794088, 2.034443935795705}
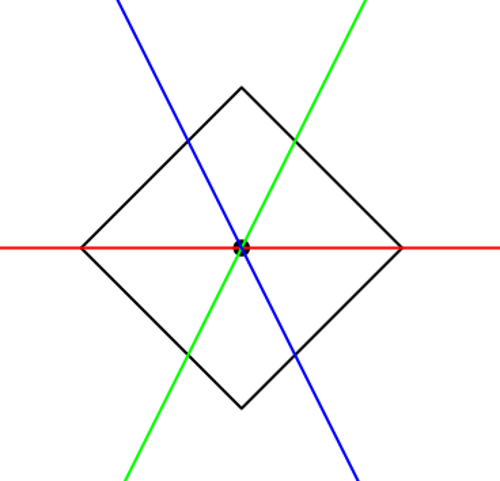
Ein Quadrat wurde um 45 Grad gedreht.
[
Quelle ]