Guten Tag. Ich habe diesen Artikel speziell für Studenten des Kurses "Algorithmen für Entwickler" in OTUS geschrieben und möchte ihn heute mit allen Lesern unseres Blogs teilen.Ein Schachpferd steht auf einem Schachbrett und schaut nachdenklich ins Schachbrett.
Wie viele verschiedene Züge kann er machen?

Gelobt sei der Erfinder des Schachs, auf dem Brett befinden sich
64 Zellen.
Lob an den Computerarchitekten -
ulong Typ hat auch
64 Bit.
Dieser Zufall musste passieren!
Die geniale Idee liegt auf der Hand - das
gesamte Board in
einer ganzen Zahl zu speichern! Es gibt sogar einen speziellen Begriff für diese Lösung -
Bitboard - ein
Bitboard .
Wie
kann man mit dieser Idee
schnell die Anzahl der Züge eines Schachpferdes ermitteln?
Gegeben:
knightNr -
Zellennummer des Brettes, auf dem sich das Pferd befindet (von 0 bis 63).
Es ist notwendig:
movesCount - die Anzahl der Felder, in die es gehen kann (von 2 bis 8).
Algorithmus
1. Konvertieren Sie die
Käfignummer des Pferdes in
ulong - Wert des
BitboardsknightNr ->
knightBits2. Setzen Sie Bits für alle möglichen Bewegungen des Pferdes
knightBits ->
movesBits3.Zählen Sie die Anzahl der Einheitenbits
movesBits ->
movesCount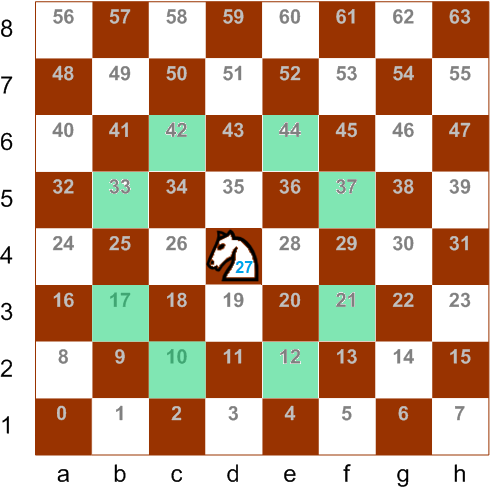
Der erste Schritt ist sehr einfach: Sie müssen das Null-Bit um die angegebene Anzahl von Positionen nach links verschieben.
ulong knightBits = 1 << knightNr;
Der zweite Schritt ist etwas komplizierter. Ein Pferd kann in 8 verschiedene Richtungen gehen. Wir betrachten diese Offsets nicht "horizontal / vertikal", sondern nach Bitpositionen. Das heißt, wir überlegen, wie viele Positionen Sie benötigen, um das Startbit für jede Bewegung zu verschieben. Dann "addieren" wir alles mit einer logischen "oder" -Operation.
Fangen wir an, die Züge von links nach rechts aufzulisten:
movesBits = knightBits << 6 | knightBits >> 10
Richtig, cool!?
Leider gibt es "schwarze Löcher" an den Rändern des Brettes. Nach diesem Algorithmus kann man zum Beispiel von Zelle a4 (Bit # 24) zu Zelle g2 (Bit # 14 = 24 - 10) gelangen. Dieser Sprung ist eine
Teleportation eines kugelförmigen Schachpferdes in einem Vakuum auf einem Brett durch ein Schwarzes Loch zu den extremen Vertikalen ...
Um den Quantensprung des Pferdes über die Brettkante auszuschließen, ist es notwendig, die Extrembänder nach dem Bewegen zu "trennen". Zum Beispiel ist es für Züge +6 und -10 (zwei Zellen nach links) erforderlich, die erhaltenen Werte für die g- und h-Vertikalen zu löschen, da Sie nicht in diesen Vertikalen enden können, nachdem Sie zwei Züge lang nach links gegangen sind.
Dazu benötigen wir 4-Bit-Gitterkonstanten, in denen alle Bits außer den angegebenen Vertikalen auf 1 gesetzt sind. Nämlich:
ulong nA = 0xFeFeFeFeFeFeFeFe; ulong nAB = 0xFcFcFcFcFcFcFcFc; ulong nH = 0x7f7f7f7f7f7f7f7f; ulong nGH = 0x3f3f3f3f3f3f3f3f;
An der Ober- und Unterseite des Schachbretts befinden sich auch „Schwarze Löcher“, die das Pferd vollständig absorbieren, sodass sie nicht separat überprüft werden müssen.
Nun sieht der Algorithmus zur Erzeugung zulässiger Pferdebewegungen so aus:
movesBits = nGH & (knightBits << 6 | knightBits >> 10) | nH & (knightBits << 15 | knightBits >> 17) | nA & (knightBits << 17 | knightBits >> 15) | nAB & (knightBits << 10 | knightBits >> 6);
Es funktioniert sehr (!) Schnell.
Ein paar Zecken - und wir haben eine Bitmap aller möglichen Pferdeabenteuer. Das Erstaunlichste ist, dass dieser Algorithmus auch dann funktioniert, wenn sich mehrere Pferde auf dem Brett befinden. Er generiert sofort alle möglichen Bewegungen für alle Pferde! Stimmt, großartig!
Es bleibt die Anzahl der Bits zu zählen
Am einfachsten ist es, die Zahl 1 Bit nach rechts zu schieben und die zu zählen. Schwierigkeit - 64 Operationen. Speicher - 64 Bits.
Am schnellsten erstellen Sie einen Cache / Array mit 65536 Elementen, in den die Anzahl der Bits für jeden Index von 0 bis 65535 geschrieben wird. Fügen Sie 4 Elemente aus diesem Array hinzu, die den nächsten 16-Bit-Segmenten der Zahl entsprechen.
Schwierigkeit - 4 Operationen. Speicher - 64 Kilobyte.
Wir werden jedoch
den schwierigsten Weg betrachten , dessen Komplexität der Anzahl der einzelnen Bits in der Zahl entspricht. Da es nicht viele Züge gibt, ist dieser Ansatz für uns der optimalste.
Zunächst stellen wir fest, dass wir durch Subtrahieren einer Einheit von einer Zahl alle „richtigen“ Nullen in Einheiten und die äußerste Einheit in Nullen umwandeln:
1001010100010000 - 1 = 1001010100001111
Wenden Sie als Nächstes die logische „und“ -Operation für diese Zahlen an:
1001010100010000 & 1001010100001111 = 1001010100000000
Wie Sie sehen, setzen wir auf solch knifflige Weise die Einheit ganz rechts auf Null zurück. Wiederholen Sie diesen Vorgang, bis wir als Ergebnis Null erhalten. Wie viele Iterationen, so viele einzelne Bits. Stimmt, großartig!
So ist dieser Algorithmus vollständig geschrieben:
int movesCount = 0; while (movesBits != 0) { movesBits &= (movesBits - 1); movesCount ++; }
Das Problem ist gelöst!
Diese Aufgabe hat eine andere, sehr einfache, rein logische Lösung: den Abstand des Ritters von der Kante des Schachbretts zu bestimmen (in der Ecke befinden sich 2 Züge, in der Nähe der Kante 3 bis 6 Züge, in der Mitte von 8 Zügen). Aber wenn wir das Problem auf diese Weise "frontal" lösen würden, wüssten wir nichts über das Bitboard, über vertikale Bitmasken, über den Algorithmus zum schnellen Zählen einzelner Bits und über Schwarze Löcher für kugelförmige Pferde im Vakuum ...
Jetzt wissen wir alles darüber. Das Leben eines Schachprogrammierers ist reicher und bedeutungsvoller geworden, Prost!
Do-it-yourself-Aufgabe: Mach dasselbe für den Schachkönig.