Geekly articles weekly

Monte Carlo Blackjack Strategieoptimierung

Die Übersetzung des Artikels wurde speziell für Studierende des Kurses Maschinelles Lernen erstellt .



Verstärktes Training eroberte die Welt der künstlichen Intelligenz. Ausgehend von AlphaGo und AlphaStar werden immer mehr Aktivitäten, die zuvor vom Menschen dominiert wurden, jetzt von KI-Agenten auf der Grundlage von Verstärkungstraining erobert. Kurz gesagt, diese Erfolge hängen von der Optimierung der Aktionen des Agenten in einer bestimmten Umgebung ab, um eine maximale Belohnung zu erzielen. In den letzten Artikeln von GradientCrescent haben wir uns mit verschiedenen grundlegenden Aspekten des verstärkten Lernens befasst, von den Grundlagen der Banditensysteme und politischen Ansätzen zur Optimierung des belohnungsbasierten Verhaltens in Markov-Umgebungen . All diese Ansätze erforderten eine vollständige Kenntnis unserer Umwelt. Die dynamische Programmierung setzt beispielsweise eine vollständige Wahrscheinlichkeitsverteilung aller möglichen Zustandsübergänge voraus. In der Realität stellen wir jedoch fest, dass die meisten Systeme nicht vollständig interpretiert werden können und dass Wahrscheinlichkeitsverteilungen aufgrund von Komplexität, inhärenter Unsicherheit oder Einschränkungen der Rechenkapazitäten nicht explizit erhalten werden können. Betrachten Sie als Analogie die Aufgabe des Meteorologen - die Anzahl der Faktoren, die bei der Wettervorhersage eine Rolle spielen, kann so groß sein, dass es unmöglich ist, die Wahrscheinlichkeit genau zu berechnen.

In solchen Fällen sind Lehrmethoden wie Monte Carlo die Lösung. Der Begriff Monte Carlo wird allgemein verwendet, um einen beliebigen Ansatz zur Schätzung von Zufallsstichproben zu beschreiben. Mit anderen Worten, wir sagen kein Wissen über unsere Umwelt voraus, sondern lernen aus Erfahrungen, indem wir beispielhafte Folgen von Zuständen, Handlungen und Belohnungen durchlaufen, die durch die Interaktion mit der Umwelt entstehen. Diese Methoden arbeiten, indem sie die vom Modell während des normalen Betriebs zurückgegebenen Belohnungen direkt beobachten, um den Durchschnittswert seiner Bedingungen zu beurteilen. Interessanterweise können wir auch ohne Kenntnis der Dynamik der Umgebung (die als Wahrscheinlichkeitsverteilung von Zustandsübergängen betrachtet werden sollte) immer noch ein optimales Verhalten erzielen, um die Belohnungen zu maximieren.

Betrachten Sie als Beispiel das Ergebnis eines Würfels mit 12 Würfeln. Wenn wir diese Würfe als einen einzelnen Zustand betrachten, können wir diese Ergebnisse mitteln, um näher an das tatsächlich vorhergesagte Ergebnis heranzukommen. Je größer die Stichprobe, desto genauer nähern wir uns dem tatsächlich erwarteten Ergebnis.


Die durchschnittlich erwartete Menge von 12 Würfeln für 60 Schüsse beträgt 41,57

Diese Art der stichprobenbasierten Bewertung mag dem Leser vertraut erscheinen, da eine solche Stichprobe auch für k-Banditensysteme durchgeführt wird. Anstatt verschiedene Banditen zu vergleichen, werden Monte-Carlo-Methoden verwendet, um verschiedene Richtlinien in Markov-Umgebungen zu vergleichen und den Wert des Staates zu bestimmen, während eine bestimmte Richtlinie befolgt wird, bis die Arbeit abgeschlossen ist.

Monte-Carlo-Schätzung des Zustandswertes


Monte-Carlo-Methoden sind eine Möglichkeit, im Kontext des verstärkenden Lernens die Signifikanz des Zustands eines Modells durch Mittelung der Stichprobenergebnisse zu bewerten. Aufgrund der Notwendigkeit eines Endzustands sind Monte-Carlo-Methoden von Natur aus auf episodische Umgebungen anwendbar. Aufgrund dieser Einschränkung werden Monte-Carlo-Methoden normalerweise als "autonom" betrachtet, bei denen alle Aktualisierungen nach Erreichen des Terminalzustands durchgeführt werden. Es kann eine einfache Analogie zum Herausfinden eines Weges aus einem Labyrinth gegeben werden - ein autonomer Ansatz würde den Agenten dazu zwingen, das Ende zu erreichen, bevor er die gesammelten Zwischenerfahrungen nutzt, um die Zeit zu verkürzen, die er benötigt, um durch das Labyrinth zu gehen. Andererseits wird der Agent bei der Online-Annäherung sein Verhalten bereits während des Durchgangs des Labyrinths ständig ändern. Vielleicht bemerkt er, dass die grünen Korridore zu Sackgassen führen und entscheidet, sie beispielsweise zu meiden. In einem der folgenden Artikel werden wir Online-Ansätze diskutieren.

Die Monte-Carlo-Methode kann wie folgt formuliert werden:



Um die Funktionsweise der Monte-Carlo-Methode besser zu verstehen, sehen Sie sich das folgende Zustandsübergangsdiagramm an. Die Belohnung für jeden Zustandsübergang wird in schwarz angezeigt, ein Abzinsungsfaktor von 0,5 wird darauf angewendet. Lassen Sie uns den tatsächlichen Wert des Zustands beiseite legen und uns auf die Berechnung der Ergebnisse eines Wurfs konzentrieren.


Zustandsübergangsdiagramm. Die Statusnummer wird rot angezeigt, das Ergebnis ist schwarz.
Da der Endzustand ein Ergebnis gleich 0 zurückgibt, berechnen wir das Ergebnis jedes Zustands, beginnend mit dem Endzustand (G5). Bitte beachten Sie, dass wir den Abzinsungsfaktor auf 0,5 eingestellt haben, was zu einer Gewichtung gegenüber den späteren Staaten führt.



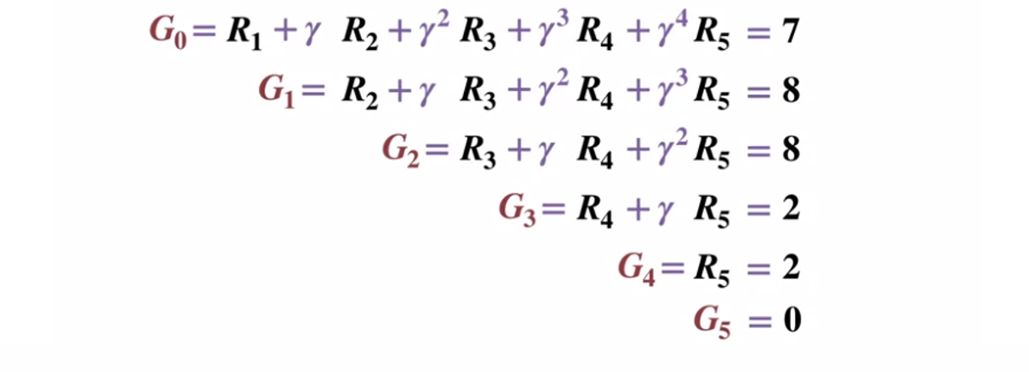
Oder allgemeiner:



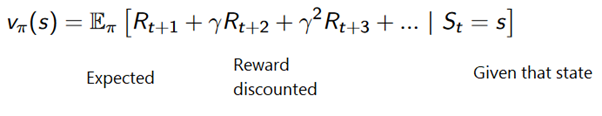
Um zu vermeiden, dass alle Ergebnisse in der Liste gespeichert werden, können Sie den Statuswert in der Monte-Carlo-Methode schrittweise aktualisieren, indem Sie eine Gleichung verwenden, die einige Ähnlichkeiten mit der herkömmlichen Gradientenabnahme aufweist:


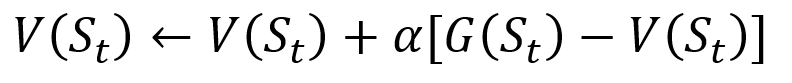Inkrementelle Aktualisierung nach Monte Carlo. S ist der Zustand, V ist sein Wert, G ist sein Ergebnis und A ist der Schrittwertparameter.

Im Rahmen des Verstärkungstrainings können Monte-Carlo-Methoden sogar als Erster Besuch oder Jeder Besuch klassifiziert werden. Kurz gesagt, der Unterschied zwischen beiden besteht darin, wie oft ein Bundesstaat in einer Passage vor dem Monte-Carlo-Update besucht werden kann. Die Monte-Carlo-Methode für den ersten Besuch schätzt den Wert aller Zustände als Durchschnittswert der Ergebnisse nach einzelnen Besuchen in jedem Zustand vor Abschluss, während die Monte-Carlo-Methode für jeden Besuch den Durchschnitt der Ergebnisse nach n Besuchen bis zum Abschluss ermittelt. Wir werden den Monte-Carlo-Erstbesuch in diesem Artikel wegen seiner relativen Einfachheit verwenden.

Monte-Carlo-Richtlinienverwaltung


Wenn das Modell die Richtlinie nicht bereitstellen kann, kann Monte Carlo zum Bewerten von Zustandsaktionswerten verwendet werden. Dies ist nützlicher als nur die Bedeutung der Zustände, da die Idee der Bedeutung jeder Aktion (q) in einem gegebenen Zustand es dem Agenten ermöglicht, automatisch eine Richtlinie aus Beobachtungen in einer unbekannten Umgebung zu formulieren.

Genauer gesagt können wir Monte Carlo verwenden, um q (s, a, pi) , das erwartete Ergebnis, wenn wir von Zustand s ausgehen, Aktion a und die nachfolgende Richtlinie Pi zu schätzen. Die Monte-Carlo-Methoden bleiben unverändert, mit der Ausnahme, dass für einen bestimmten Zustand eine zusätzliche Dimension von Maßnahmen ergriffen wird. Es wird angenommen, dass ein Zustand-Aktion (en, ein) -Paar während der Passage besucht wird, wenn Zustand s jemals besucht wird und Aktion a darin ausgeführt wird. Ebenso kann die Bewertung von Wertaktionen mit den Ansätzen „Erster Besuch“ und „Jeder Besuch“ durchgeführt werden.

Wie bei der dynamischen Programmierung können wir eine generalisierte Iterationsrichtlinie (GPI) verwenden, um eine Richtlinie aus der Beobachtung von Zustandsaktionswerten zu bilden.



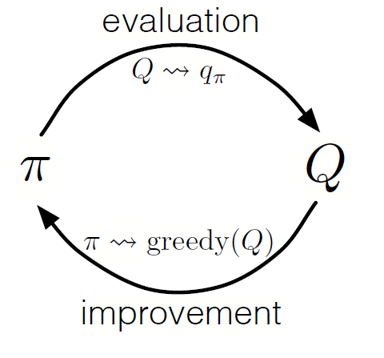
Indem wir die Schritte der Politikevaluierung und -verbesserung abwechseln und Nachforschungen anstellen, um sicherzustellen, dass alle möglichen Maßnahmen ergriffen werden, können wir für jede Bedingung die optimale Politik erzielen. Beim Monte-Carlo-GPI erfolgt diese Drehung normalerweise nach dem Ende jedes Durchgangs.


Monte Carlo GPI

Blackjack-Strategie


Um besser zu verstehen, wie die Monte-Carlo-Methode in der Praxis bei der Bewertung verschiedener Zustandswerte funktioniert, führen wir das Beispiel eines Blackjack-Spiels Schritt für Schritt vor. Lassen Sie uns zunächst die Regeln und Bedingungen für unser Spiel festlegen:

  • Wir werden nur gegen den Dealer spielen, es wird keine anderen Spieler geben. Dadurch können wir die Hände des Händlers als Teil der Umwelt betrachten.
  • Der Wert von Karten mit Zahlen, die den Nennwerten entsprechen. Der Wert der Bildkarten: Bube, König und Dame ist 10. Der Wert des Asses kann 1 oder 11 sein, abhängig von der Wahl des Spielers.
  • Beide Seiten erhalten zwei Karten. Zwei Spielerkarten liegen offen, eine der Karten des Dealers liegt ebenfalls offen.
  • Das Ziel des Spiels ist, dass die Anzahl der Karten auf der Hand <= 21 ist. Ein Wert größer als 21 ist ein Fehlschlag. Wenn beide Seiten einen Wert von 21 haben, wird das Spiel unentschieden gespielt.
  • Nachdem der Spieler seine Karten und die Karte des ersten Dealers gesehen hat, kann er wählen, ob er eine neue Karte ("noch") oder nicht ("genug") nehmen möchte, bis er mit der Summe der Kartenwerte auf seiner Hand zufrieden ist.
  • Dann zeigt der Dealer seine zweite Karte - wenn der sich ergebende Betrag weniger als 17 beträgt, muss er Karten nehmen, bis er 17 Punkte erreicht hat, wonach er die Karte nicht mehr nimmt.

Mal sehen, wie die Monte-Carlo-Methode mit diesen Regeln funktioniert.

Runde 1.


Du gewinnst insgesamt 19. Aber du versuchst, das Glück am Schwanz zu fangen, eine Chance zu nutzen, 3 zu bekommen und pleite zu gehen. Als Sie pleite gingen, hatte der Dealer nur eine offene Karte mit einer Summe von 10. Dies kann wie folgt dargestellt werden:



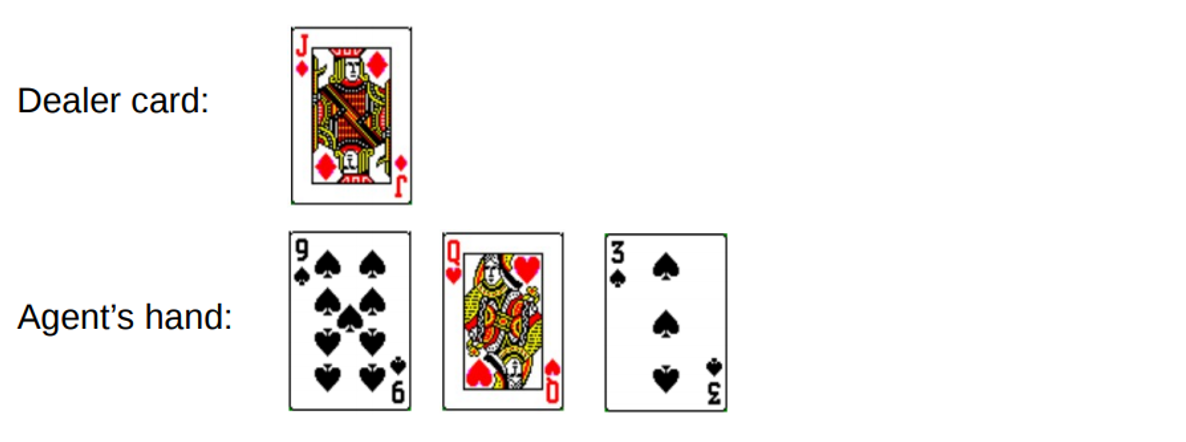
Wenn wir pleite gehen, ist unsere Belohnung für die Runde -1. Legen wir diesen Wert als Ergebnis der Rückgabe des vorletzten Status im folgenden Format fest [Betrag des Agenten, Betrag des Händlers, Ass?]:



Nun, jetzt haben wir kein Glück mehr. Gehen wir zu einer anderen Runde über.

Runde 2.


Sie geben insgesamt 19 ein. Diesmal entscheiden Sie sich, den Vorgang abzubrechen. Der Dealer wählt 13, nimmt eine Karte und geht pleite. Der vorletzte Zustand kann wie folgt beschrieben werden.



Beschreiben wir die Bedingungen und Belohnungen, die wir in dieser Runde erhalten haben:



Mit dem Ende der Passage können wir nun die Werte aller unserer Staaten in dieser Runde anhand der berechneten Ergebnisse aktualisieren. Bei einem Abzinsungsfaktor von 1 verteilen wir einfach unsere neue Handbelohnung, wie dies bei den vorherigen Zustandsübergängen der Fall war. Da der Zustand V (19, 10, nein) zuvor -1 zurückgegeben hat, berechnen wir den erwarteten Rückgabewert und weisen ihn unserem Zustand zu:


Endzustandswerte zur Demonstration am Beispiel Blackjack .

Implementierung


Lassen Sie uns ein Blackjack-Spiel mit der Monte-Carlo-Methode des ersten Besuchs schreiben, um alle möglichen Statuswerte (oder verschiedene verfügbare Kombinationen) im Spiel mit Python herauszufinden. Unser Ansatz basiert auf dem Ansatz von Sudharsan et. al. . Wie immer finden Sie den gesamten Code aus dem Artikel auf unserem GitHub .

Um die Implementierung zu vereinfachen, werden wir Gym von OpenAI verwenden. Stellen Sie sich die Umgebung als Schnittstelle zum Starten von Blackjack mit einem Minimum an Code vor. Auf diese Weise können wir uns auf die Implementierung von verstärktem Lernen konzentrieren. Praktischerweise werden alle gesammelten Informationen über die Zustände, Aktionen und Belohnungen in den Beobachtungsvariablen gespeichert, die während der aktuellen Spielsitzungen angesammelt werden.

Beginnen wir mit dem Import aller Bibliotheken, die wir zum Abrufen und Sammeln unserer Ergebnisse benötigen.

import gym import numpy as np from matplotlib import pyplot import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from collections import defaultdict from functools import partial %matplotlib inline plt.style.use('ggplot')

Als nächstes initialisieren wir unser Fitnessstudio und definieren eine Richtlinie, die die Aktionen unseres Agenten koordiniert. Tatsächlich nehmen wir die Karte solange weiter, bis der Betrag auf der Hand 19 oder mehr erreicht hat. Danach hören wir auf.

 #Observation here encompassess all data about state that we need, as well as reactions to it env = gym.make('Blackjack-v0') #Define a policy where we hit until we reach 19. # actions here are 0-stand, 1-hit def sample_policy(observation): score, dealer_score, usable_ace = observation return 0 if score >= 19 else 1

Definieren wir eine Methode zum Generieren von Passdaten mithilfe unserer Richtlinie. Wir speichern Informationen über den Status, die ergriffenen Maßnahmen und die Vergütung für die Maßnahme.

 def generate_episode(policy, env): # we initialize the list for storing states, actions, and rewards states, actions, rewards = [], [], [] # Initialize the gym environment observation = env.reset() while True: # append the states to the states list states.append(observation) # now, we select an action using our sample_policy function and append the action to actions list action = sample_policy(observation) actions.append(action) # We perform the action in the environment according to our sample_policy, move to the next state observation, reward, done, info = env.step(action) rewards.append(reward) # Break if the state is a terminal state (ie done) if done: break return states, actions, rewards

Definieren wir abschließend den ersten Besuch der Monte-Carlo-Vorhersagefunktion. Zunächst initialisieren wir ein leeres Wörterbuch, um die aktuellen Statuswerte und ein Wörterbuch zu speichern, in dem die Anzahl der Datensätze für jeden Status in verschiedenen Durchläufen gespeichert wird.

 def first_visit_mc_prediction(policy, env, n_episodes): # First, we initialize the empty value table as a dictionary for storing the values of each state value_table = defaultdict(float) N = defaultdict(int)

Für jeden Durchgang rufen wir unsere generate_episode- Methode auf, um Informationen zu den Statuswerten und den Belohnungen abzurufen, die nach dem Status eingehen. Wir initialisieren auch die Variable, um unsere inkrementellen Ergebnisse zu speichern. Dann erhalten wir die Belohnung und den aktuellen Statuswert für jeden während des Passes besuchten Status und erhöhen unsere variablen Erträge um den Wert der Belohnung pro Schritt.

 for _ in range(n_episodes): # Next, we generate the epsiode and store the states and rewards states, _, rewards = generate_episode(policy, env) returns = 0 # Then for each step, we store the rewards to a variable R and states to S, and we calculate for t in range(len(states) — 1, -1, -1): R = rewards[t] S = states[t] returns += R # Now to perform first visit MC, we check if the episode is visited for the first time, if yes, #This is the standard Monte Carlo Incremental equation. # NewEstimate = OldEstimate+StepSize(Target-OldEstimate) if S not in states[:t]: N[S] += 1 value_table[S] += (returns — value_table[S]) / N[S] return value_table

Ich möchte Sie daran erinnern, dass wir seit dem ersten Besuch von Monte Carlo einen Staat in einem Durchgang besuchen. Aus diesem Grund prüfen wir das Statuswörterbuch unter bestimmten Bedingungen, um festzustellen, ob der Status besucht wurde. Wenn diese Bedingung erfüllt ist, können wir den neuen Wert mithilfe der zuvor definierten Prozedur zum Aktualisieren der Statuswerte mithilfe der Monte-Carlo-Methode berechnen und die Anzahl der Beobachtungen für diesen Status um 1 erhöhen. Anschließend wiederholen wir den Vorgang für den nächsten Durchgang, um schließlich den Durchschnittswert des Ergebnisses zu erhalten .

Lassen Sie uns das, was wir haben, durchgehen und die Ergebnisse betrachten!

 value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000) for i in range(10): print(value.popitem())


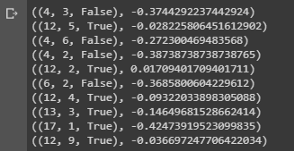Abschluss einer Stichprobe, die die Zustandswerte verschiedener Kombinationen der Hände beim Blackjack zeigt.

Wir können weiterhin Monte-Carlo-Beobachtungen für 5000 Pässe durchführen und eine Verteilung der Statuswerte erstellen, die die Werte einer beliebigen Kombination in den Händen des Spielers und des Dealers beschreibt.

 def plot_blackjack(V, ax1, ax2): player_sum = np.arange(12, 21 + 1) dealer_show = np.arange(1, 10 + 1) usable_ace = np.array([False, True]) state_values = np.zeros((len(player_sum), len(dealer_show), len(usable_ace))) for i, player in enumerate(player_sum): for j, dealer in enumerate(dealer_show): for k, ace in enumerate(usable_ace): state_values[i, j, k] = V[player, dealer, ace] X, Y = np.meshgrid(player_sum, dealer_show) ax1.plot_wireframe(X, Y, state_values[:, :, 0]) ax2.plot_wireframe(X, Y, state_values[:, :, 1]) for ax in ax1, ax2: ax.set_zlim(-1, 1) ax.set_ylabel('player sum') ax.set_xlabel('dealer sum') ax.set_zlabel('state-value') fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8),subplot_kw={'projection': '3d'}) axes[0].set_title('state-value distribution w/o usable ace') axes[1].set_title('state-value distribution w/ usable ace') plot_blackjack(value, axes[0], axes[1])


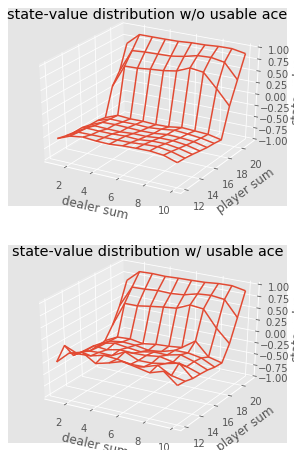Visualisierung der Zustandswerte verschiedener Kombinationen beim Blackjack.

Fassen wir also zusammen, was wir gelernt haben.

  • Auf Stichproben basierende Lernmethoden ermöglichen es uns, Zustands- und Aktionszustandswerte ohne Übergangsdynamik einfach durch Stichproben zu bewerten.
  • Monte-Carlo-Ansätze basieren auf einer zufälligen Auswahl des Modells, der Beobachtung der vom Modell zurückgegebenen Belohnungen und der Erfassung von Informationen während des normalen Betriebs, um den Durchschnittswert seiner Zustände zu bestimmen.
  • Mit Monte-Carlo-Methoden ist eine verallgemeinerte Iterationsrichtlinie möglich.
  • Der Wert aller möglichen Kombinationen in den Händen des Spielers und des Dealers beim Blackjack kann unter Verwendung mehrerer Monte-Carlo-Simulationen geschätzt werden, was den Weg für optimierte Strategien ebnet.

Damit ist die Einführung in die Monte-Carlo-Methode abgeschlossen. In unserem nächsten Artikel werden wir uns mit Lehrmethoden der Form Temporal Difference Learning befassen.

Quellen:


Sutton et. al, Verstärkungslernen
White et. al, Fundamentals of Reinforcement Learning, Universität Alberta
Silva et. al, Reinforcement Learning, UCL
Platt et. Al, Northeaster University

Das ist alles. Wir sehen uns auf dem Platz !

Source: https://habr.com/ru/post/de477042/

More articles:


All Articles