Die Optimierung von Compilern ist die Basis moderner Software: Sie ermöglichen es Programmierern, Code in einer Sprache zu schreiben, die sie verstehen, und ihn dann in Code umzuwandeln, der von Geräten effizient ausgeführt werden kann. Die Aufgabe der Optimierung von Compilern besteht darin, die Funktionsweise des von Ihnen geschriebenen Eingabeprogramms zu verstehen und ein Ausgabeprogramm zu erstellen, das dasselbe nur schneller ausführt.
In diesem Artikel werden einige der grundlegenden Inferenztechniken zur Optimierung von Compilern vorgestellt: Entwerfen eines Programms, mit dem der Compiler problemlos arbeiten kann; Welche Reduzierungen können in Ihrem Programm vorgenommen werden und wie können Sie sie verwenden, um es zu reduzieren und zu beschleunigen?
Programmoptimierer können überall ausgeführt werden: im Rahmen eines umfangreichen Kompilierungsprozesses (
Scala Optimizer ); als separates Programm, das nach dem Compiler und vor der Ausführung gestartet wird (
Proguard ); oder als Teil einer Laufzeitumgebung, die ein Programm während seiner Ausführung optimiert (
JVM JIT-Compiler ). Die Einschränkungen bei der Arbeit von Optimierern variieren je nach Situation, aber sie haben eine Aufgabe: das Eingabeprogramm zu nehmen und es in das Ausgabeprogramm umzuwandeln, was dasselbe tut, aber schneller.
Zunächst werden einige Beispiele für Optimierungen des Programmentwurfs vorgestellt, damit Sie verstehen, was Optimierer normalerweise tun und wie sie manuell ausgeführt werden. Anschließend werden verschiedene Möglichkeiten zur Präsentation von Programmen betrachtet und schließlich die Algorithmen und Techniken analysiert, mit denen Sie Programme analysieren und dann kleiner und schneller machen können.
Programmentwurf
Alle Beispiele werden in Java gegeben. Diese Sprache ist sehr verbreitet und wird zu einem relativ einfachen Assembler kompiliert -
Java Bytecode . Wir werden also eine gute Grundlage schaffen, dank derer wir Kompilierungsoptimierungstechniken anhand realer, ausführbarer Beispiele untersuchen können. Alle unten beschriebenen Techniken sind in fast allen anderen Programmiersprachen anwendbar.
Betrachten Sie zunächst einen Programmentwurf. Es enthält verschiedene Logik, registriert das Standardergebnis innerhalb des Prozesses und gibt das berechnete Ergebnis zurück. Das Programm selbst ist nicht sinnvoll, wird jedoch als Beispiel dafür verwendet, was unter Beibehaltung des vorhandenen Verhaltens optimiert werden kann:
static int main(int n){ int count = 0, total = 0, multiplied = 0; Logger logger = new PrintLogger(); while(count < n){ count += 1; multiplied *= count; if (multiplied < 100) logger.log(count); total += ackermann(2, 2); total += ackermann(multiplied, n); int d1 = ackermann(n, 1); total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
Im Moment gehen wir davon aus, dass dieses Programm alles ist, was wir haben, kein anderer Teil des Codes nennt es. Es gibt einfach Daten in
main , führt sie aus und gibt das Ergebnis zurück. Nun optimieren wir dieses Programm.
Optimierungsbeispiele
Typguss und Inlining
Möglicherweise haben Sie bemerkt, dass die
logger Variable einen ungenauen Typ hat: Trotz der
Logger Bezeichnung können wir aufgrund des Codes den Schluss ziehen, dass es sich um eine bestimmte Unterklasse handelt -
PrintLogger :
- Logger logger = new PrintLogger(); + PrintLogger logger = new PrintLogger();
Jetzt wissen wir, dass
PrintLogger , und wir wissen, dass der Aufruf von
logger.log eine einzige Implementierung haben kann. Sie können inline:
- if (multiplied < 100) logger.logcount(); + if (multiplied < 100) System.out.println(count);
Dadurch wird das Programm reduziert, indem die nicht verwendete
ErrLogger Klasse entfernt wird, die nicht verwendet wird, und indem verschiedene Methoden des
public Logger log gelöscht werden, da wir es an einer einzigen Stelle des Aufrufs
ErrLogger .
Koagulationskonstanten
Während der Programmausführung ändern sich
count und
total , aber
multiplied nicht: Sie beginnt bei
0 und wird jedes Mal durch
multiplied = multiplied * count , wobei sie gleich
0 bleibt. Sie können es also im gesamten Programm durch
0 ersetzen:
static int main(int n){ - int count = 0, total = 0, multiplied = 0; + int count = 0, total = 0; PrintLogger logger = new PrintLogger(); while(count < n){ count += 1; - multiplied *= count; - if (multiplied < 100) System.out.println(count); + if (0 < 100) logger.log(count); total += ackermann(2, 2); - total += ackermann(multiplied, n); + total += ackermann(0, n); int d1 = ackermann(n, 1); - total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
Als Ergebnis sehen wir, dass
d1 * multiplied immer
0 , was bedeutet, dass
total += d1 * multiplied nichts bewirkt und gelöscht werden kann:
- total += d1 * multiplied
Entfernung des toten Codes
Nachdem Sie
multiplied gefaltet haben und festgestellt haben, dass
total += d1 * multiplied nichts bewirkt, können Sie die Definition von
int d1 entfernen:
- int d1 = ackermann(n, 1);
Dies ist nicht mehr Teil des Programms, und da es sich bei
ackermann um eine reine Funktion handelt, hat die Deinstallation keine Auswirkungen auf das Ergebnis des Programms.
In ähnlicher
logger.log wird der
logger selbst nach dem Inlining von
logger.log nicht mehr verwendet und kann entfernt werden:
- PrintLogger logger = new PrintLogger();
Astentfernung
Nun hängt der erste bedingte Übergang in unserem Zyklus von
0 < 100 . Da dies immer zutrifft, können Sie einfach die Bedingung entfernen:
- if (0 < 100) System.out.println(count); + System.out.println(count);
Jeder bedingte Übergang, der immer wahr ist, kann in den Hauptteil der Bedingung integriert werden. Bei Übergängen, die immer falsch sind, können Sie die Bedingung zusammen mit ihrem Hauptteil löschen.
Teilberechnung
Nun analysieren wir die drei verbleibenden Anrufe bei
ackermann :
total += ackermann(2, 2); total += ackermann(0, n); int d2 = ackermann(n, count);
- Der erste hat zwei konstante Argumente. Die Funktion ist rein und nach vorläufiger Berechnung sollte
ackermann(2, 2) gleich 7. - Der zweite Aufruf hat ein konstantes Argument
0 und ein unbekanntes n . Sie können es an die Definition von ackermann , und es stellt sich heraus, dass die Funktion immer n + 1. zurückgibt, wenn m 0 ist n + 1.
- Beim dritten Aufruf sind beide Argumente unbekannt:
n und count . Lassen wir sie vorerst an Ort und Stelle.
Vorausgesetzt, der Anruf bei
ackermann ist wie folgt definiert:
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Sie können es vereinfachen, um:
- total += ackermann(2, 2); + total += 7 - total += ackermann(0, n); + total += n + 1 int d2 = ackermann(n, count);
Verspätete Planung
Die Definition von
d2 nur im
if (count % 2 == 0) bedingten
if (count % 2 == 0) . Da die
ackermann Berechnung sauber ist, können Sie diesen Aufruf an einen bedingten
ackermann weiterleiten, sodass er erst verarbeitet wird, wenn er verwendet wird:
- int d2 = ackermann(n, count); - if (count % 2 == 0) total += d2; + if (count % 2 == 0) { + int d2 = ackermann(n, count); + total += d2; + }
Dadurch wird die Hälfte der Aufrufe von
ackermann(n, count) vermieden und die Programmausführung beschleunigt.
Zum Vergleich: Die Funktion
System.out.println ist nicht sauber.
System.out.println bedeutet, dass sie nicht innerhalb oder außerhalb von bedingten Sprüngen übertragen werden kann, ohne die Semantik des Programms zu ändern.
Optimiertes Ergebnis
Nachdem wir alle Optimierungen gesammelt haben, erhalten wir den folgenden Quellcode:
static int main(int n){ int count = 0, total = 0; while(count < n){ count += 1; System.out.println(count); total += 7; total += n + 1; if (count % 2 == 0) { total += d2; int d2 = ackermann(n, count); } } return total; } static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Obwohl wir manuell optimiert haben, kann dies alles automatisch erfolgen. Das folgende ist das dekompilierte Ergebnis des Prototyp-Optimierers, den ich für JVM-Programme geschrieben habe:
static int main(int var0) { new Demo.PrintLogger(); int var1 = 0; int var3; for(int var2 = 0; var2 < var0; var2 = var3) { System.out.println(var3 = 1 + var2); int var10000 = var3 % 2; int var7 = var1 + 7 + var0 + 1; var1 = var10000 == 0 ? var7 + ackermann(var0, var3) : var7; } return var1; } static int ackermann__I__TI1__I(int var0) { if (var0 == 0) return 2; else return ackermann(var0 - 1, var0 == 0 ? 1 : ackermann__I__TI1__I(var0 - 1);); } static int ackermann(int var0, int var1) { if (var0 == 0) return var1 + 1; else return var1 == 0 ? ackermann__I__TI1__I(var0 - 1) : ackermann(var0 - 1, ackermann(var0, var1 - 1)); } static class PrintLogger implements Demo.Logger {} interface Logger {}
Der dekompilierte Code unterscheidet sich geringfügig von der manuell optimierten Version. Etwas, das der Compiler nicht optimieren konnte (zum Beispiel ein nicht verwendeter Aufruf von
new PrintLogger ), aber etwas wurde etwas anders gemacht (zum Beispiel sind
ackermann und
ackermann__I__TI1__I ). Im Übrigen hat der automatische Optimierer das Gleiche getan wie ich, indem er die darin eingebettete Logik verwendet hat.
Es stellt sich die Frage: Wie?
Zwischenansichten
Wenn Sie versuchen, Ihr eigenes Optimierungsprogramm zu erstellen, ist die erste Frage möglicherweise die wichtigste: Was ist ein „Programm“?
Zweifellos sind Sie es gewohnt, Programme als Quellcode zu schreiben und zu ändern. Sie haben sie definitiv in Form von kompilierten Binärdateien ausgeführt, vielleicht sogar die Binärdateien debuggt. Möglicherweise sind Sie auf Programme in Form eines
Syntaxbaums , eines
Codes mit drei Adressen , eines
A-Normalen , eines
Continuation Passing-Stils oder einer
einzelnen statischen Zuweisung gestoßen .
Es gibt einen ganzen Zoo mit verschiedenen Darstellungen von Programmen. Hier werden die wichtigsten Möglichkeiten zur Darstellung eines „Programms“ im Optimierer erläutert.
Quellcode
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Nicht kompilierter Quellcode ist auch eine Darstellung Ihres Programms. Es ist relativ kompakt, für Menschen lesbar, hat aber zwei Nachteile:
- Der Quellcode enthält alle Details der Namen und Formatierungen, die für den Programmierer wichtig, für den Computer jedoch unbrauchbar sind.
- Fehlerhafte Programme in Form von Quellcode sind viel zahlreicher als korrekte. Während der Optimierung müssen Sie sicherstellen, dass Ihr Programm vom richtigen Eingabequellcode in den richtigen Ausgabequellcode konvertiert wird.
Diese Faktoren erschweren es dem Optimierer, mit dem Programm in Form von Quellcode zu arbeiten. Ja, Sie
können ein solches Programm beispielsweise mit
regulären Ausdrücken konvertieren, um Muster
zu identifizieren und zu ersetzen. Der erste von zwei Faktoren macht es jedoch schwierig, Muster mit einer Fülle von irrelevanten Details zuverlässig zu identifizieren. Und der zweite Faktor erhöht die Wahrscheinlichkeit, verwirrt zu werden und ein falsches Programm zu erhalten, erheblich.
Diese Einschränkungen sind für Programmkonverter akzeptabel, die unter menschlicher Aufsicht ausgeführt werden, z. B. wenn Sie
Codemod zum Umgestalten und Transformieren der Codebasis verwenden können. Sie können den Quellcode jedoch nicht als primäres Modell eines automatisierten Optimierers verwenden.
Abstrakte Syntaxbäume
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) )

Abstract Syntax Trees (AST) ist ein weiteres gängiges Zwischenformat. Sie befinden sich im nächsten Schritt der Abstraktionsleiter im Vergleich zum Quellcode. In der Regel verwirft AST alle Formatierungen, Einrückungen und Kommentare des Quellcodes, behält jedoch die Namen lokaler Variablen bei, die in abstrakteren Darstellungen verworfen werden.
Wie der Quellcode leidet AST unter der Möglichkeit, unnötige Informationen zu codieren, die die tatsächliche Semantik des Programms nicht beeinflussen. Beispielsweise sind die folgenden zwei Codefragmente semantisch identisch. Sie unterscheiden sich nur in den Namen der lokalen Variablen, haben aber immer noch unterschiedliche ASTs:
static int ackermannA(int m, int n){ int p = n; int q = m; if (q == 0) return p + 1; else if (p == 0) return ackermannA(q - 1, 1); else return ackermannA(q - 1, ackermannA(q, p - 1)); } Block( Assign("p", Ident("n")), Assign("q", Ident("m")), IfElse( cond = BinOp(Ident("q"), "==", Literal(0)), then = Return(BinOp(Ident("p"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("p"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("q"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("q"), "-", Literal(1)), Call("ackermann", Ident("q"), BinOp(Ident("p"), "-", Literal(1))) ) ) ) ) ) static int ackermannB(int m, int n){ int r = n; int s = m; if (s == 0) return r + 1; else if (r == 0) return ackermannB(s - 1, 1); else return ackermannB(s - 1, ackermannB(s, r - 1)); } Block( Assign("r", Ident("n")), Assign("s", Ident("m")), IfElse( cond = BinOp(Ident("s"), "==", Literal(0)), then = Return(BinOp(Ident("r"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("r"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("s"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("s"), "-", Literal(1)), Call("ackermann", Ident("s"), BinOp(Ident("r"), "-", Literal(1))) ) ) ) ) )
Der entscheidende Punkt ist, dass ASTs zwar eine Baumstruktur haben, aber Knoten enthalten, die sich semantisch nicht wie Bäume verhalten: Die Werte von
Ident("r") und
Ident("s") nicht durch den Inhalt ihrer Teilbäume bestimmt, sondern durch die vorgelagerten
Assign("r", ...) Knoten
Assign("r", ...) und
Assign("s", ...) . Tatsächlich gibt es zusätzliche semantische Beziehungen zwischen
Ident und
Assign , die genauso wichtig sind wie Kanten in der AST-Baumstruktur:

Diese Verbindungen bilden eine verallgemeinerte Graphstruktur, einschließlich Zyklen bei rekursiven Definitionen von Funktionen.
Bytecode
Da wir Java als Hauptsprache gewählt haben, werden kompilierte Programme als Java-Bytecode in .class-Dateien gespeichert.
Erinnern Sie sich an unsere
ackermann Funktion:
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Es kompiliert zu diesem Bytecode:
0: iload_0 1: ifne 8 4: iload_1 5: iconst_1 6: iadd 7: ireturn 8: iload_1 9: ifne 20 12: iload_0 13: iconst_1 14: isub 15: iconst_1 16: invokestatic ackermann:(II)I 19: ireturn 20: iload_0 21: iconst_1 22: isub 23: iload_0 24: iload_1 25: iconst_1 26: isub 27: invokestatic ackermann:(II)I 30: invokestatic ackermann:(II)I 33: ireturn
Die Java Virtual Machine (JVM), auf der der Java-Bytecode ausgeführt wird, ist eine Maschine mit einer Kombination aus Stapel und Registern: Es gibt einen Stapel von Operanden (STACK), in denen Werte bearbeitet werden, und ein Array lokaler Variablen (LOCALS), in denen diese Werte gespeichert werden können. Die Funktion beginnt mit N Parametern in den ersten N Slots lokaler Variablen. Während der Ausführung verschiebt die Funktion die Daten auf den Stapel, bearbeitet sie, setzt sie in die Variablen zurück und ruft
return auf, um den Wert vom Operandenstapel an den Aufrufer zurückzugeben.
Wenn Sie den obigen Bytecode mit Anmerkungen versehen, um Werte darzustellen, die zwischen dem Stapel und der lokalen Variablentabelle verschoben werden, sieht dies folgendermaßen aus:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Hier habe
a1 mit
a0 und
a1 der Funktion die Argumente präsentiert, die in der Tabelle LOCALS ganz am Anfang der Funktion gespeichert sind.
1 repräsentiert Konstanten, die über
iconst_1 geladen wurden und von
v1 bis
v7 berechnete Zwischenwerte. Es gibt drei
ireturn , die
v1 ,
v3 und
v7 . Diese Funktion definiert keine anderen lokalen Variablen, daher speichert das LOCALS-Array nur Eingabeargumente.
Wir haben oben zwei Optionen für unsere Funktion gesehen -
ackermannA und
ackermannB . Also schauen sie im Bytecode:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| |
Da der Quellcode zwei Argumente akzeptiert und in lokale Variablen einfügt, verfügt der Bytecode über die entsprechenden Anweisungen, um die Argumentwerte aus den LOCAL-Indizes 0 und 1 zu laden und unter den Indizes 2 und 3 zu speichern. Der Bytecode interessiert sich jedoch nicht für die Namen Ihrer lokalen Variablen: Er funktioniert mit von ihnen ausschließlich wie bei Indizes im LOCALS-Array. Daher haben
ackermannA und
ackermannB identische Bytecodes. Das ist logisch, weil sie semantisch äquivalent sind!
ackermannA und
ackermannB werden jedoch nicht in denselben Bytecode wie der ursprüngliche
ackermann kompiliert: Obwohl der Bytecode von den Namen lokaler Variablen abstrahiert wird, wird er vom Laden und Speichern in / aus diesen Variablen immer noch nicht vollständig abstrahiert. Für uns ist es immer noch wichtig, wie sich die Werte entlang LOCALS und STACK bewegen, obwohl sie das tatsächliche Verhalten des Programms nicht beeinflussen.
Neben der fehlenden Abstraktion vom Laden / Speichern hat der Bytecode einen weiteren Nachteil: Wie die meisten linearen Assembler ist er hinsichtlich seiner Kompaktheit sehr optimiert und kann bei Optimierungen sehr schwierig zu modifizieren sein.
Schauen wir uns zur Verdeutlichung den Bytecode der ursprünglichen
ackermann Funktion an:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Nehmen wir eine grobe Änderung vor: Lassen Sie den Funktionsaufruf
30: invokestatic ackermann:(II)I verwende sein erstes Argument nicht. Und dann kann dieser Aufruf durch den entsprechenden Aufruf
30: invokestatic ackermann2:(I)I , der nur ein Argument
30: invokestatic ackermann2:(I)I . Dies ist eine übliche Optimierung, die es ermöglicht, mithilfe der "Entfernung toten Codes" jeden Code zu
30: invokestatic ackermann:(II)I der zur Berechnung des ersten Arguments
30: invokestatic ackermann:(II)IDazu müssen wir nicht nur die Anweisung
30 ersetzen, sondern auch die Liste der Anweisungen betrachten und verstehen, wo das erste Argument berechnet wird (
v4 in
STACK ), und es auch löschen. Wir kehren von den Anweisungen
30 bis
22 und von
22 bis
21 und
20 . Die endgültige Version:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | - 20: iload_0 |a0|a1| | - 21: iconst_1 |a0|a1| | - 22: isub |a0|a1| | 23: iload_0 |a0|a1| |a0| 24: iload_1 |a0|a1| |a0|a1| 25: iconst_1 |a0|a1| |a0|a1| 1| 26: isub |a0|a1| |a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v6| - 30: invokestatic ackermann:(II)I |a0|a1| |v7| + 30: invokestatic ackermann2:(I)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Wir können immer noch eine so einfache Änderung an einer einfachen
ackermann Funktion vornehmen. Bei den großen Funktionen, die in realen Projekten verwendet werden, wird es jedoch viel schwieriger sein, zahlreiche miteinander verbundene Änderungen vorzunehmen. Im Allgemeinen kann jede kleine semantische Änderung an Ihrem Programm zahlreiche Änderungen im gesamten Bytecode erforderlich machen.
Möglicherweise stellen Sie fest, dass wir die oben beschriebene Änderung durch Analysieren der Werte in LOCALS und STACK vorgenommen haben: Wir haben beobachtet, wie
v4 von Anweisung
22 an Anweisung
30 wird und
22 Daten zu
a0 und
1 , die von den Anweisungen
21 und
20 . Diese Werte werden nach dem Prinzip des Graphen zwischen LOCALS und STACK übertragen: von der Anweisung zur Berechnung des Wertes bis zum Ort seiner weiteren Verwendung.
Wie die
Ident /
Assign Paare in unseren ASTs bilden die Werte, die zwischen LOCALS und STACK übergeben werden, eine Grafik zwischen den Berechnungspunkten der Werte und den Verwendungspunkten. Warum arbeiten wir nicht direkt mit dem Diagramm?
Datenflussdiagramme
Datenflussdiagramme sind die nächste Abstraktionsebene nach dem Bytecode. Wenn wir unseren Syntaxbaum um
Ident /
Assign Beziehungen erweitern oder verfolgen, wie der Bytecode Werte zwischen LOCALS und STACK verschiebt, können wir ein Diagramm erstellen. Für die
ackermann Funktion sieht es so aus:

Im Gegensatz zum AST- oder Java-Stack-Bytecode-Bytecode verwenden Datenflussdiagramme nicht das Konzept einer „lokalen Variablen“. Stattdessen enthält das Diagramm direkte Verbindungen zwischen jedem Wert und dem Ort, an dem er verwendet wird. Bei der Analyse von Bytecode ist es häufig erforderlich, LOCALS und STACK abstrakt zu interpretieren, um zu verstehen, wie sich die Werte bewegen. Bei der AST-Analyse wird der Baum verfolgt und mit einer Symboltabelle gearbeitet, die
Assign /
Ident Assoziationen enthält. Das Analysieren von Datenflussgraphen ist häufig eine direkte Verfolgung von Übergängen - die reine Idee, Werte zu verschieben, ohne die Hüllen eines Programms zu präsentieren.
ackermann auch einfacher zu bearbeiten als linearer Bytecode: Wenn Sie einen Knoten durch einen
ackermann Aufruf durch einen
ackermann Aufruf ersetzen und eines der Argumente
ackermann2 wird lediglich der Diagrammknoten (grün markiert) geändert und einer der Eingabelinks zusammen mit den Transitknoten (rot markiert) gelöscht:

Wie Sie sehen können, führt eine kleine Änderung im Programm (Ersetzen von
ackermann(int n, int m) durch
ackermann2(int m) ) zu einer relativ lokalisierten Änderung im Datenstromdiagramm.
Im Allgemeinen ist das Arbeiten mit Diagrammen viel einfacher als mit linearem Bytecode oder AST: Sie sind einfach zu analysieren und zu ändern.
Diese Beschreibung von Diagrammen enthält nicht viele Details: Zusätzlich zur tatsächlichen physischen Darstellung des Diagramms gibt es viele andere Möglichkeiten zur Modellierung des Zustands und der Flusssteuerung, die schwieriger zu handhaben sind und über den Umfang des Artikels hinausgehen. Ich habe auch eine Reihe von Details zum Transformieren von Diagrammen weggelassen, z. B. Hinzufügen und Entfernen von Verknüpfungen, Vorwärts- und Rückwärtsübergängen, horizontalen und vertikalen Übergängen (in Breite und Tiefe) usw. Wenn Sie Algorithmen studiert haben, sollte Ihnen dies alles bekannt sein .
Schließlich haben wir die Konvertierungsalgorithmen von linearem Bytecode zu Grafik und dann von Grafik zurück zu Bytecode weggelassen. Dies ist an sich eine interessante Aufgabe, aber wir überlassen sie Ihnen für ein unabhängiges Studium.
Analyse
Nachdem wir die Idee des Programms erhalten haben, müssen wir es analysieren: Finden Sie einige Fakten heraus, mit denen Sie das Programm transformieren können, ohne sein Verhalten zu ändern. Viele der oben diskutierten Optimierungen basieren auf der Analyse des Programms:
- Konstante Faltung: Arbeitet das Ergebnis des Ausdrucks mit einem bekannten konstanten Wert? Ist die Ausdrucksberechnung rein?
- Typumwandlung und Inlining: Ist ein Methodenaufruftyp ein Typ mit einer einzelnen Implementierung der aufgerufenen Methode?
- : ?
- : «»? - ? ?
- : , ?
, , , . , , , .
, , , — , . .
(Inference Lattice)
, . , «» - :
Integer ? String ? Array[Float] ? PrintLogger ?
CharSequence ? String , - StringBuilder ?
Any , , ?
:

: ,
"hello" String ,
String CharSequence .
"hello" , (Singleton Type) — . :

, , . , . , , ,
String StringBuilder , , :
CharSequence . ,
0 ,
1 ,
2 , ,
Integer .

, , :

, , . , .
count
main :
static int main(int n){ int count = 0, multiplied = 0; while(count < n){ if (multiplied < 100) logger.log(count); count += 1; multiplied *= count; } return ...; }
ackermann ,
count ,
multiplied logger . :

,
count 0 block0 .
block1 , ,
count < n : ,
block3 return ,
block2 ,
count 1 count ,
block1 . ,
< false ,
block3 .
?
block0 . , count = 0.
block1 , , n ( , Integer ), , if . block2 block3.block3 , , block1b , block2 , , block1c . , block2 count , 1 count.- ,
count 0 1 : count Integer. - :
block1 n count Integer .
block2 , count Integer + 1 -> Integer . , count Integer , .
multiplied
,
multiplied :
block0 . , multiplied 0.
block1 , , . block2 block3 ( ).
block2 , block2 ( 0 ) count ( Integer ). 0 * Integer -> 0 , multiplied 0.
block1 block2 . multiplied 0 , .
multiplied 0 , , :
multiplied < 100 true.
if (multiplied < 100) logger.log(count); logger.log(count) .
- ,
multiplied , , 0 .
:

:

:
static int main(int n){ int count = 0; while(count < n){ logger.log(count); count += 1; } return ...; }
, , , , .
multiplied -> 0 , , . , , . , .
, . :
count ,
multiplied . ,
multiplied count ,
count multiplied . , .
, — : , . , ( ) . .
while , ,
O( ) . (, ) , , .
, .
, . , , , , .
. :
static int main(int n){ return called(n, 0); } static int called(int x, int y){ return x * y; }
:

main :
main(n)
called(n, 0)
called(n, 0) 0
main(n) 0
, , . .
,
called(n, 0) 0 , :

:
static int main(int n){ return 0; }
: A B, C, D, D C, B, D A. A B B A, A A, , !
, Java:
public static Any factorial(int n) { if (n == 1) { return 1; } else { return n * factorial(n - 1); } }
n int ,
Any : . ,
factorial int (
Integer ).
factorial ,
factorial factorial , ! ?
Bottom
Bottom :

« , , ».
Bottom factorial :

block0 . n Integer , 1 1 , n == 1 , true false .
true : return 1 .
false n - 1 n Integer .
factorial — , Bottom .
* n: Integer factorial : Bottom Bottom .
return Bottom .factorial 1 Bottom , 1 .
1 factorial , Bottom .
Integer * 1 Integer .
return Integer .factorial Integer 1 , Integer .
factorial , Integer . * n: Integer factorial: Integer , Integer , .
factorial Integer , , .
, .
Bottom , , .
* :
(n: Integer) * (factorial: Bottom)
(n: Integer) * (factorial: 1)
(n: Integer) * (factorial: Integer)
multiplied ,
O( ) . , , .
— , « ». , (« »), , (« »). .
main :
static int main(int n){ int count = 0, total = 0, multiplied = 0; while(count < n){ if (multiplied > 100) count += 1; count += 1; multiplied *= 2; total += 1; } return count; }
,
if (multiplied > 100) multiplied *= count multiplied *= 2 . .
, :
multiplied > 100 true , count += 1 («»).
total , («»).
, :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
, .
:

, , :
block0 ,
block1 , ,
block1b , ,
block1c , ,
return block3 .
,
multiplied -> 0 , :

Folgendes ist passiert:

,
block1b (
0 > 100 )
true .
false block1c (
if ):
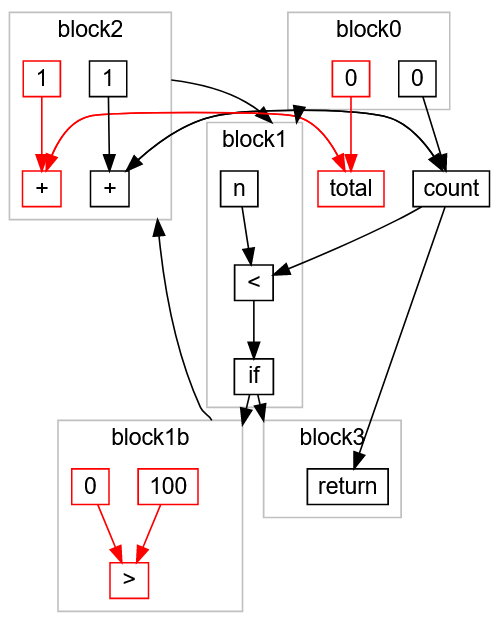
, « »
total > , - , , . ,
return ,
:
> ,
100 ,
0 block1b ,
total ,
0 ,
+ 1 ,
total block0 block2 . Folgendes ist passiert:

«» :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
Fazit
:
- -.
- , .
- , . .
- : «» «» , , .
- : , .
- , .
, , .
, . . , :