Ich veröffentliche weiterhin meine Vorlesungen, die ursprünglich für Studenten gedacht waren, die im Fachgebiet "Digitale Geologie" studieren. Dies ist die dritte Veröffentlichung aus dem Zyklus am Hub, der erste Artikel war eine Einführung, es ist nicht erforderlich, gelesen zu werden. Um diesen Artikel zu verstehen, ist es jedoch erforderlich, die Einführung in lineare Gleichungssysteme zu lesen, auch wenn Sie wissen, was es ist, da ich mich viel auf Beispiele aus dieser Einführung beziehen werde.

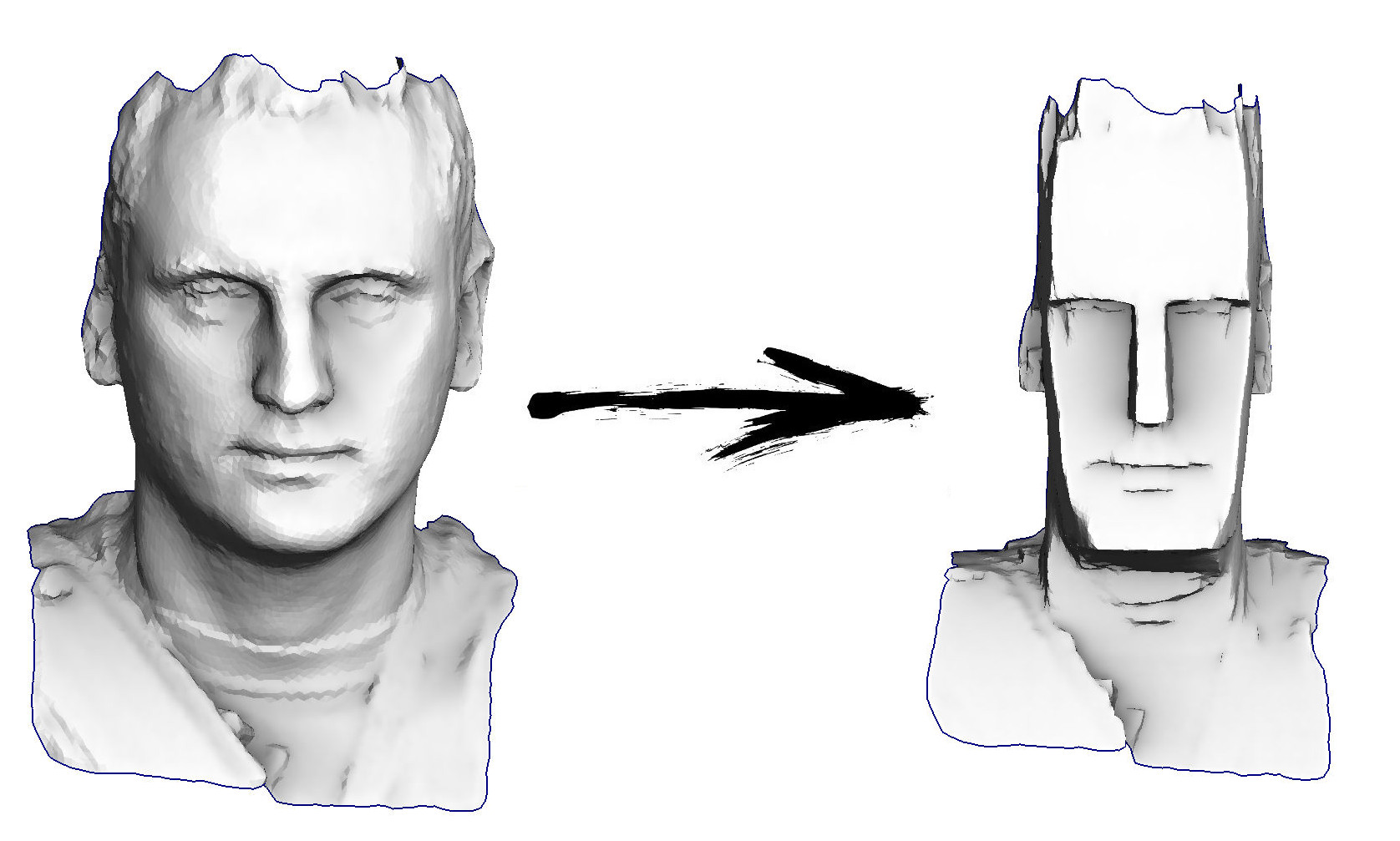
Also die Aufgabe für heute: die einfachste Geometrie-Bearbeitung lernen, um zum Beispiel meinen Kopf in ein Idol von der Osterinsel verwandeln zu können:



Aktueller Vorlesungsplan:

• Bildungsprogramm zur Wahrscheinlichkeitstheorie (Einführungsartikel, fakultativ)
  
• Einführung in lineare Gleichungssysteme
  
• Minimierung quadratischer Formen und Beispiele für OLS-Probleme
  
• Von den kleinsten Plätzen zu den neuronalen Netzen
  

Hier befindet sich das offizielle Kursprogramm. Das Buch ist noch nicht fertig, ich erstelle langsam Artikel, die auf Habré veröffentlicht wurden.

In diesem Artikel besteht mein Hauptwerkzeug darin, das Minimum an quadratischen Funktionen zu finden. Bevor wir dieses Tool verwenden, müssen Sie jedoch wissen, wo er den Ein- / Ausschalter hat. Aktualisieren Sie zunächst den Speicher und rufen Sie ab, was Matrizen sind, was eine positive Zahl ist und was eine Ableitung ist.

Matrizen und Zahlen

In diesem Text werde ich reichlich Matrixnotation verwenden, also erinnern wir uns, was es ist. Schauen Sie nicht weiter in den Text, halten Sie einige Sekunden inne und versuchen Sie zu formulieren, was eine Matrix ist.

Verschiedene Matrixinterpretationen

Die Antwort ist sehr einfach. Die Matrix ist nur ein Schrank, in dem Meerrettich aufbewahrt wird. Jede Scheiße liegt in ihrer Zelle, Zellen sind in Zeilen in Zeilen und Spalten gruppiert. In unserem speziellen Fall sind die üblichen reellen Zahlen Mist; der einfachste Weg für einen Programmierer $$$A$ etwas mögen

float A[m][n]; 

Warum werden solche Speicher benötigt? Was beschreiben sie? Vielleicht werde ich dich verärgern, aber die Matrix selbst beschreibt nichts, sie speichert. Zum Beispiel können Sie darin die Koeffizienten beliebiger Funktionen speichern. Vergessen wir die Matrizen für eine Sekunde und stellen uns vor, dass wir eine Zahl haben $$$a$ . Was bedeutet es Ja, der Teufel weiß ... Zum Beispiel kann es sich um einen Koeffizienten in einer Funktion handeln, der eine Zahl als Eingabe und eine andere Zahl als Ausgabe verwendet:

$$

$$f (x): \ mathbb R \ rightarrow \ mathbb R$$

Ein Mathematiker könnte eine Version einer solchen Funktion schreiben wie

$$

$$f (x) = ax$$

Nun, in der Welt der Programmierer würde das so aussehen:

 float f(float x) { return a*x; } 

Warum aber eine solche Funktion und nicht eine ganz andere? Nehmen wir noch einen!

$$

$$f (x) = ax ^ 2$$

Da ich über Programmierer angefangen habe, muss ich ihren Code schreiben :)

 float f(float x) { return x*a*x; } 

Eine dieser Funktionen ist linear und die zweite quadratisch. Welches ist richtig? Nein, die Nummer selbst $$$a$ definiert es nicht, es speichert nur einen Wert! Welche Funktion brauchst du, baue eine davon.

Dasselbe passiert mit Matrizen, das sind Speicher, die benötigt werden, falls nicht genügend einzelne Zahlen (Skalare) vorhanden sind, eine Art Erweiterung von Zahlen. Über den Matrizen sind genau wie über den Zahlen die Operationen der Addition und Multiplikation definiert.

Stellen wir uns vor, wir hätten eine Matrix $$$A$ Zum Beispiel Größe 2x2:

$$

$$A = \ begin {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix}$$

Diese Matrix an sich hat keine Bedeutung, sie kann beispielsweise als Funktion interpretiert werden

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2, \ quad f (x) = Ax$$

 vector<float> f(vector<float> x) { return vector<float>{a11*x[0] + a12*x[1], a21*x[0] + a22*x[1]}; } 

Diese Funktion konvertiert einen zweidimensionalen Vektor in einen zweidimensionalen Vektor. Grafisch ist es praktisch, dies als Bildkonvertierung darzustellen: Wir geben das Bild dem Eingang und am Ausgang erhalten wir seine gedehnte und / oder gedrehte (möglicherweise sogar gespiegelte!) Version. Sehr bald werde ich ein Bild mit verschiedenen Beispielen für eine solche Interpretation von Matrizen geben.

Und kann die Matrix $$$A$ Stellen Sie sich eine Funktion vor, die einen zweidimensionalen Vektor in einen Skalar umwandelt:

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R, \ quad f (x) = x ^ \ top A x = \ sum \ limits_i \ sum \ limits_ja_ {ij} x_i x_j$$

Beachten Sie, dass die Potenzierung bei Vektoren nicht sehr definiert ist, sodass ich nicht schreiben kann $$$x ^ 2$ , wie er bei gewöhnlichen Zahlen schrieb. Ich kann es nur all jenen empfehlen, die es nicht gewohnt sind, Matrixmultiplikationen einfach zu jonglieren, die Matrixmultiplikationsregel noch einmal in Erinnerung zu rufen und den Ausdruck zu überprüfen $$$x ^ \ top A x$ generell erlaubt und gibt wirklich einen skalar am ausgang. Dazu können Sie beispielsweise explizit eckige Klammern setzen $$$x ^ \ top A x = (x ^ \ top A) x$ . Ich erinnere Sie daran, dass wir haben $$$x$ Ist ein Vektor der Dimension 2 (gespeichert in einer Matrix der Dimension 2x1), schreiben wir explizit alle Dimensionen:

$$

$$\ underbrace {\ underbrace {\ left (\ underbrace {x ^ \ top} _ {1 \ times 2} \ times \ underbrace {A} _ {2 \ times 2} \ right)} _ {1 \ times 2} \ times \ underbrace {x} _ {2 \ times 1}} _ {1 \ times 1}$$

Wir kehren in die warme und flauschige Welt der Programmierer zurück und können dieselbe quadratische Funktion wie folgt schreiben:

 float f(vector<float> x) { return x[0]*a11*x[0] + x[0]*a12*x[1] + x[1]*a21*x[0] + x[1]*a22*x[1]; } 

Was ist eine positive Zahl?

Jetzt werde ich eine sehr dumme Frage stellen: Was ist eine positive Zahl? Wir haben ein großartiges Werkzeug, das Prädikat genannt wird $$$>$ . Aber nehmen Sie sich Zeit, um diese Nummer zu beantworten $$$a$ positiv wenn und nur wenn $$$a> 0$ Das wäre zu einfach. Definieren wir Positivität wie folgt:

Definition 1

Nummer $$$a$ positiv wenn und nur wenn für alle ungleich null echt $$$x \ in \ mathbb R, \ x \ neq 0$ Die Bedingung ist erfüllt $$$ax ^ 2> 0$ .

Es sieht ziemlich knifflig aus, gilt aber perfekt für Matrizen:

Definition 2

Quadratische Matrix $$$A$ heißt positiv definit wenn, für jeden ungleich Null $$$x$ Die Bedingung ist erfüllt $$$x ^ \ top A x> 0$ Das heißt, die entsprechende quadratische Form ist mit Ausnahme des Ursprungs überall streng positiv.

Warum brauche ich Positivität? Wie ich am Anfang des Artikels erwähnt habe, besteht mein Hauptwerkzeug darin, nach den Minimums der quadratischen Funktionen zu suchen. Aber um zumindest zu suchen, wäre es nicht schlecht, wenn es existiert! Zum Beispiel eine Funktion $$$f (x) = - x ^ 2$ das Minimum existiert offensichtlich nicht, da die Zahl -1 nicht positiv ist, und $$$f (x)$ nimmt mit dem Wachstum endlos ab $$$x$ : Zweige einer Parabel $$$f (x)$ schau runter. Positive bestimmte Matrizen sind insofern gut, als die entsprechenden quadratischen Formen ein Paraboloid mit einem (eindeutigen) Minimum bilden. Die folgende Abbildung zeigt sieben verschiedene Beispiele für Matrizen. $$$2 \ mal 2$ , sowohl positiv bestimmt als auch symmetrisch, und nicht so. Obere Reihe: Interpretation von Matrizen als Funktionen $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2$ . Mittlere Reihe: Interpretation von Matrizen als Funktionen $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R$ .



Daher werde ich mit positiven bestimmten Matrizen arbeiten, die eine Verallgemeinerung von positiven Zahlen sind. Außerdem sind speziell in meinem Fall die Matrizen auch symmetrisch! Es ist merkwürdig, dass Menschen, die von positiver Gewissheit sprechen, häufig auch Symmetrie meinen, was indirekt durch die folgende (für das Verständnis des nachfolgenden Textes optionale) Beobachtung erklärt werden kann.

Lyrischer Exkurs zur Symmetrie von Matrizen quadratischer Formen

Schauen wir uns die quadratische Form an $$$x ^ \ top M x$ für eine beliebige Matrix $$$M$ ; dann zu $$$M$ Addiere und subtrahiere sofort die Hälfte der transponierten Version:

$$

$$M = \ underbrace {\ frac {1} {2} (M + M ^ \ top)} _ {: = M_s} + \ underbrace {\ frac {1} {2} (MM ^ \ top)} _ { : = M_a} = M_s + M_a$$

Matrix $$$M_s$ symmetrisch: $$$M_s ^ \ top = M_s$ ; Matrix $$$M_a$ antisymmetrisch: $$$M_a ^ \ top = -M_a$ . Eine bemerkenswerte Tatsache ist, dass für jede antisymmetrische Matrix die entsprechende quadratische Form identisch Null ist. Dies ergibt sich aus folgender Beobachtung:

$$

$$q = x ^ \ top M_a x = (x ^ \ top M_a ^ \ top x) ^ \ top = - (x ^ \ top M_a x) ^ \ top = -q$$

Das heißt, die quadratische Form $$$x ^ \ top M_a x$ gleichzeitig gleich $$$q$ und $$$-q$ , was nur möglich ist wenn $$$q \ äquiv 0$ . Daraus folgt für eine beliebige Matrix $$$M$ entsprechende quadratische Form $$$x ^ \ top M x$ kann durch eine symmetrische Matrix ausgedrückt werden $$$M_s$ :

$$

$$x ^ \ top M x = x ^ \ top (M_s + M_a) x = x ^ \ top M_s x + x ^ \ top M_a x = x ^ \ top M_s x.$$

Wir suchen ein Minimum einer quadratischen Funktion

Kehren wir kurz zur eindimensionalen Welt zurück. Ich möchte ein Minimum an Funktion finden $$$f (x) = ax ^ 2 - 2bx$ . Nummer $$$a$ positiv, daher gibt es ein Minimum; um es zu finden, setzen wir die entsprechende Ableitung auf Null: $$$\ frac {d} {dx} f (x) = 0$ . Unterscheiden Sie die eindimensionale quadratische Funktion der Arbeit ist nicht: $$$\ frac {d} {dx} f (x) = 2ax - 2b = 0$ ; Also läuft unser Problem darauf hinaus, die Gleichung zu lösen $$$ax-b = 0$ , wo wir durch schreckliche Anstrengungen eine Lösung finden $$$x ^ * = b / a$ . Die folgende Abbildung zeigt die Äquivalenz zweier Probleme: Lösung $$$x ^ *$ Gleichungen $$$ax-b = 0$ fällt mit der Lösung der Gleichung zusammen $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ .



Ich tendiere dazu, dass unser globales Ziel darin besteht, quadratische Funktionen zu minimieren, aber wir sprechen über kleinste Quadrate. Gleichzeitig können wir aber auch lineare Gleichungen (und lineare Gleichungssysteme) lösen. Und es ist sehr cool, dass eines dem anderen entspricht!

Wir müssen nur noch sicherstellen, dass diese Äquivalenz in der eindimensionalen Welt auch für den Fall gilt $$$n$ Variablen. Um dies zu verifizieren, beweisen wir zunächst drei Theoreme.

Drei Theoreme oder unterschiedliche Matrixausdrücke

Der erste Satz besagt, dass Matrizen $$$1 \ mal 1$ Invarianten in Bezug auf die Umsetzung:

Satz 1

$$$x \ in \ mathbb R \ Rightarrow x ^ \ top = x$

Der Beweis ist so kompliziert, dass ich ihn der Kürze halber weglassen muss, aber versuche, ihn selbst zu finden.

Der zweite Satz erlaubt es uns, lineare Funktionen zu differenzieren. Im Fall einer reellen Funktion einer Variablen wissen wir das $$$\ frac {d} {dx} (bx) = b$ aber was passiert bei einer realen funktion $$$n$ Variablen?

Satz 2

$$$\ nabla b ^ \ top x = \ nabla x ^ \ top b = b$

Das ist keine Überraschung, nur eine Matrixaufnahme desselben Schulergebnisses. Der Beweis ist sehr einfach, schreiben Sie einfach die Definition des Gradienten:

$$

$$\ nabla (b ^ \ top x) = \ begin {bmatrix} \ frac {\ partial (b ^ \ top x)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partial (b ^ \ top x)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} \ frac {\ partial (b_1 x_1 + \ dots + b_n x_n)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partiell (b_1 x_1 + \ dots + b_n x_n)} {\ partiell x_n} \ end {bmatrix} = \ begin {bmatrix} b_1 \\ \ vdots \\ b_n \ end {bmatrix} = b$$

Anwendung des ersten Satzes $$$b ^ \ top x = x ^ \ top b$ vervollständigen wir den Beweis.

Nun gehen wir zu quadratischen Formen über. Wir wissen das im Fall einer reellen Funktion einer Variablen $$$\ frac {d} {dx} (ax ^ 2) = 2ax$ , und was passiert bei einer quadratischen Form?

Satz 3

$$$\ nabla (x ^ \ top A x) = (A + A ^ \ top) x$

Übrigens, wenn die Matrix $$$A$ symmetrisch, dann sagt der Satz das $$$\ nabla (x ^ \ top A x) = 2Ax$ .

Dieser Beweis ist auch einfach, schreiben Sie einfach die quadratische Form als doppelte Summe:

$$

$$x ^ \ top A x = \ sum \ limits_i \ sum \ limits_j a_ {ij} x_i x_j$$

Und dann wollen wir sehen, was die partielle Ableitung dieser Doppelsumme in Bezug auf die Variable ist $$$x_i$ :
\ begin {align *}
\ frac {\ partial (x ^ \ top A x)} {\ partial x_i}
& = \ frac {\ partial} {\ partial x_i} \ left (\ sum \ limits_ {k_1} \ sum \ limits_ {k_2} a_ {k_1 k_2} x_ {k_1} x_ {k_2} \ right) = \\
& = \ frac {\ partial} {\ partial x_i} \ left (
\ underbrace {\ sum \ limits_ {k_1 \ neq i} \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_1} x_ {k_2}} _ {k_1 \ neq i, k_2 \ neq i} + \ Unterschreitung {\ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_i x_ {k_2}} _ {k_1 = i, k_2 \ neq i} +
\ underbrace {\ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} x_i} _ {k_1 \ neq i, k_2 = i} +
\ underbrace {a_ {ii} x_i ^ 2} _ {k_1 = i, k_2 = i} \ right) = \\
& = \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} + 2 a_ {ii} x_i = \\
& = \ sum \ limits_ {k_2} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1} a_ {k_1 i} x_ {k_1} = \\
& = \ sum \ limits_ {j} (a_ {ij} + a_ {ji}) x_j \\
\ end {align *}
Ich habe die doppelte Summe in vier Fälle aufgeteilt, die durch geschweifte Klammern hervorgehoben werden. Jeder dieser vier Fälle unterscheidet trivial. Es bleibt die letzte Aktion zu tun, sammeln Sie die partiellen Ableitungen im Gradientenvektor:

$$

$$\ nabla (x ^ \ top A x) = \ begin {bmatrix} \ frac {\ partial (x ^ \ top Axe)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partial (x ^ \ nach oben A x)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} \ sum \ limits_ {j} (a_ {1j} + a_ {j1}) x_j \\ \ vdots \\ \ sum \ limits_ {j} (a_ {nj} + a_ {jn}) x_j \ end {bmatrix} = (A + A ^ \ top) x$$

Das Minimum der quadratischen Funktion und die Lösung des linearen Systems

Vergessen wir nicht die Fahrtrichtung. Wir haben das mit einer positiven Zahl gesehen $$$a$ Lösen Sie bei reellen Funktionen einer Variablen die Gleichung $$$ax = b$ oder die quadratische Funktion minimieren $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ Sind ein und dasselbe.

Wir wollen den entsprechenden Zusammenhang für eine symmetrische positive definite Matrix zeigen $$$A$ .
Wir wollen also das Minimum der quadratischen Funktion finden

$$

$$\ mathrm {argmin} _ {x \ in \ mathbb R ^ n} (x ^ \ top A x - 2b ^ \ top x).$$

Genau wie in der Schule setzen wir die Ableitung auf Null:

$$

$$\ nabla (x ^ \ top A x - 2b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}.$$

Der Hamilton-Operator ist linear, daher können wir unsere Gleichung in der folgenden Form umschreiben:

$$

$$\ nabla (x ^ \ top A x) - 2 \ nabla (b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Nun wenden wir den zweiten und dritten Differenzierungssatz an:

$$

$$(A + A ^ \ top) x - 2b = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Erinnern Sie sich daran $$$A$ Wenn wir die Gleichung symmetrisch teilen, erhalten wir das System der benötigten linearen Gleichungen:

$$

$$Ax = b$$

Hurra, wenn wir von einer Variablen zu vielen wechseln, haben wir überhaupt nichts verloren und können quadratische Funktionen effektiv minimieren!

Wir gehen zu den kleinsten Quadraten

Schließlich können wir zum Hauptinhalt dieser Vorlesung übergehen. Stellen Sie sich vor, wir haben zwei Punkte in einer Ebene $$$(x_1, y_1)$ und $$$(x_2, y_2)$ , und wir wollen die Gleichung einer Linie finden, die durch diese beiden Punkte verläuft. Die Gleichung der Linie kann geschrieben werden als $$$y = \ alpha x + \ beta$ unsere Aufgabe ist es, die Koeffizienten zu finden $$$\ alpha$ und $$$\ beta$ . Diese Übung ist für die siebte bis achte Klasse der Schule. Wir schreiben das Gleichungssystem auf:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ end {split} \ right.$$

Wir haben zwei Gleichungen mit zwei Unbekannten ( $$$\ alpha$ und $$$\ beta$ ), der Rest ist bekannt.

Im Allgemeinen gibt es eine Lösung, die eindeutig ist. Der Einfachheit halber schreiben wir dasselbe System in Matrixform:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \ end {bmatrix}} _ {: = A} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \ end {bmatrix}} _ {: = b}$$

Wir erhalten eine Typgleichung $$$Ax = b$ das ist trivial gelöst $$$x ^ * = A ^ {- 1} b$ .

Stellen Sie sich nun vor, wir haben drei Punkte, durch die wir eine gerade Linie zeichnen müssen:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ alpha x_3 + \ beta & = y_3 \\ \ end {split} \ right .$$

In Matrixform ist dieses System wie folgt geschrieben:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix}} _ {: = A \, (3 \ times 2)} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x \, (2 \ times 1)} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}} _ { : = b \, (3 \ times 1)}$$

Jetzt haben wir eine Matrix $$$A$ rechteckig, und es gibt es einfach nicht umgekehrt! Dies ist völlig normal, da wir nur zwei Variablen und drei Gleichungen haben, und im allgemeinen Fall hat dieses System keine Lösung. Dies ist eine völlig normale Situation in der realen Welt, in der die Punkte Daten von verrauschten Messungen sind und wir die Parameter finden müssen $$$\ alpha$ und $$$\ beta$ das beste ungefähre Messdaten. Dieses Beispiel haben wir bereits in der ersten Vorlesung bei der Kalibrierung von Steelyard berücksichtigt. Aber dann war unsere Lösung rein algebraisch und sehr umständlich. Versuchen wir es auf eine intuitivere Weise.

Unser System kann wie folgt geschrieben werden:

$$

$$\ alpha \ underbrace {\ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix}} _ {: = \ vec {i}} + \ beta \ underbrace {\ begin {bmatrix} 1 \\ 1 \ \ 1 \ end {bmatrix}} _ {: = \ vec {j}} = \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}$$

Oder, kurz gesagt,

$$

$$\ alpha \ vec {i} + \ beta \ vec {j} = \ vec {b}.$$

Vektoren $$$\ vec i$ , $$$\ vec j$ und $$$\ vec b$ bekannt, müssen Skalare finden $$$\ alpha$ und $$$\ beta$ .
Offensichtlich lineare Kombination $$$\ alpha \ vec {i} + \ beta \ vec {j}$ erzeugt ein Flugzeug und wenn der Vektor $$$\ vec b$ Liegt nicht in dieser Ebene, dann gibt es keine genaue Lösung; Wir suchen jedoch eine ungefähre Lösung.

Definieren wir den Entscheidungsfehler als $$$\ vec {e} (\ alpha, \ beta): = \ alpha \ vec {i} + \ beta \ vec {j} - \ vec b$ . Unser Ziel ist es, solche Parameterwerte zu finden $$$\ alpha$ und $$$\ beta$ das minimiert die Länge des Vektors $$$\ vec {e} (\ alpha, \ beta)$ . Mit anderen Worten, das Problem wird geschrieben als $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ .
Hier ist eine Illustration:.



Vektoren gegeben haben $$$\ vec i$ , $$$\ vec j$ und $$$\ vec b$ versuchen wir die Länge des Fehlervektors zu minimieren $$$\ vec e$ . Offensichtlich wird seine Länge minimiert, wenn es senkrecht zu der Ebene ist, die über die Vektoren gespannt ist $$$\ vec i$ und $$$\ vec j$ .

Aber warte, wo sind die kleinsten Quadrate? Jetzt werden sie sein. Wurzelextraktionsfunktion $$$\ sqrt {\ cdot}$ eintönig daher $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ = $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ !

Es ist ziemlich offensichtlich, dass die Länge des Fehlervektors minimiert wird, wenn er senkrecht zu der über die Vektoren gestreckten Ebene ist $$$\ vec i$ und $$$\ vec j$ , was durch Gleichsetzen der entsprechenden Skalarprodukte mit Null geschrieben werden kann:

$$

$$\ left \ {\ begin {split} \ vec {i} ^ \ top \ vec {e} (\ alpha, \ beta) & = 0 \\ \ vec {j} ^ \ top \ vec {e} (\ alpha, \ beta) & = 0 \ end {split} \ right.$$

In Matrixform kann dasselbe System geschrieben werden wie

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ alpha \ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix} + \ beta \ begin {bmatrix} 1 \\ 1 \\ 1 \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix }$$

oder sonst

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix} \ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix }$$

Aber wir werden hier nicht aufhören, da der Rekord weiter reduziert werden kann:

$$

$$A ^ \ top (Axe - b) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix}$$

Und die jüngste Transformation:

$$

$$A ^ \ top Ax = A ^ \ top b.$$

Berechnen wir die Abmessungen. Matrix $$$A$ hat Größe $$$3 \ mal 2$ deshalb $$$A ^ \ top A$ hat Größe $$$2 \ mal 2$ . Matrix $$$b$ hat Größe $$$3 \ mal 1$ aber Vektor $$$A ^ \ top b$ hat Größe $$$2 \ mal 1$ . Das ist im Allgemeinen die Matrix $$$A ^ \ top A$ umkehrbar! Außerdem, $$$A ^ \ top A$ Es hat ein paar schöne Eigenschaften.

Satz 4

$$$A ^ \ top A$ symmetrisch.

Das ist gar nicht so schwer zu zeigen:

$$

$$(A ^ \ top A) ^ \ top = A ^ \ top (A ^ \ top) ^ \ top = A ^ \ top A.$$

Satz 5

$$$A ^ \ top A$ positiv semi-definit: $$$\ forall x \ in \ mathbb R ^ n \ quad x ^ \ top A ^ \ top A x \ geq 0.$

Dies folgt aus der Tatsache, dass $$$x ^ \ top A ^ \ top A x = (A x) ^ \ top A x> 0$ .

Außerdem, $$$A ^ \ top A$ positiv definitiv wenn $$$A$ hat linear unabhängige Spalten (Rang $$$A$ gleich der Anzahl der Variablen im System).

Insgesamt haben wir für ein System mit zwei Unbekannten die Minimierung einer quadratischen Funktion bewiesen $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ äquivalent zur Lösung eines linearen Gleichungssystems $$$A ^ \ top A x = A ^ \ top b$ . All diese Überlegungen gelten natürlich auch für eine beliebige andere Anzahl von Variablen, aber lassen Sie uns mit einer einfachen algebraischen Berechnung alles noch einmal kompakt zusammenschreiben. Wir beginnen mit dem Problem der kleinsten Quadrate, kommen zur Minimierung der quadratischen Funktion der vertrauten Form und schließen daraus, dass dies der Lösung eines linearen Gleichungssystems gleichkommt. Also, lass uns gehen:

$$

$$\ begin {split} \ mathrm {argmin} \ | Axe - b \ | ^ 2 & = \ mathrm {argmin} (Axe-b) ^ \ top (Axe-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top - b ^ \ oben) (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ oben A ^ \ oben A x - b ^ \ oben Ax - x ^ \ oben A ^ \ oben b + \ unterbord {b ^ \ top b} _ {\ rm const}) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - 2b ^ \ top Axe) = \\ & = \ mathrm {argmin} ( x ^ \ top \ underbrace {(A ^ \ top A)} _ {: = A '} x - 2 \ underbrace {(A ^ \ top b)} _ {: = b'} \ phantom {} ^ \ top x) \ end {split}$$

Also das Problem der kleinsten Quadrate $$$\ mathrm {argmin} \ | Axe - b \ | ^ 2$ entspricht der Minimierung einer quadratischen Funktion $$$\ mathrm {argmin} (x ^ \ top A 'x - 2b' ^ \ top x)$ mit (im allgemeinen Fall) einer symmetrischen positiven definitiven Matrix $$$A '$ Dies ist wiederum gleichbedeutend mit der Lösung eines linearen Gleichungssystems $$$A'x = b '$ . Uff. Die Theorie ist vorbei.

Lass uns weiter üben

Beispiel Eins, eindimensional

Erinnern wir uns an ein Beispiel aus einem früheren Artikel :

 # initialize the data array x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. # smooth the array values other than at indices 0,18,31 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1] + x[i+1])/2. 

Wir haben ein reguläres x-Array mit 32 Elementen, das wie folgt initialisiert wird:



Und dann führen wir das folgende Verfahren tausendmal durch: Für jede Zelle x [i] schreiben wir den Durchschnittswert benachbarter Zellen hinein: x [i] = (x [i-1] + x [i + 1]) / 2. Die einzige Ausnahme: Wir werden die Elemente des Arrays nicht mit den Nummern 0, 18 und 31 umschreiben. So sieht die Entwicklung des Arrays in den ersten 150 Iterationen aus:



Wie wir in einem früheren Artikel festgestellt haben, löst unser vierzeiliger Python-Code-Megacode das folgende lineare Gleichungssystem nach der Gauß-Seidel-Methode:



Sie fanden es heraus, aber woher kam dieses System? Welche Art von Magie? Lassen Sie uns kurz abschweifen und versuchen, ein etwas anderes System zu lösen. Ich habe noch 32 Variablen, aber jetzt möchte ich, dass sie alle gleich sind. Das ist nicht schwer aufzuschreiben, es reicht aus, ein Gleichungssystem aufzuschreiben, das besagt, dass alle benachbarten Elemente paarweise gleich sind:



Der obige Python-Code berührt im Prinzip nicht die Werte von drei Variablen: x0, x18, x31, also lassen Sie uns sie auf die rechte Seite des Gleichungssystems übertragen, d. H. Aus der Menge der Unbekannten ausschließen:



Ich lege den Anfangswert x0 = 1 fest, die erste Gleichung lautet x1 = x0 = 1, die zweite Gleichung lautet x2 = x1 = x0 = 1 und so weiter, bis wir zu Gleichung 1 = x0 = x17 = x18 = 2 kommen Oh Aber dieses System hat keine Lösung: ((

Und egal, wir sind Programmierer! Rufen wir die kleinsten Quadrate an, um Hilfe zu erhalten! Unser unlösbares System kann in Matrixform geschrieben werden $$$Ax = b$ ; Um unser System ungefähr zu lösen, reicht es aus, das System zu lösen $$$A^\top Ax=A^\top b$ .Und dann stellt sich heraus, dass dies genau das Eins-in-Eins-Gleichungssystem aus dem vorherigen Artikel ist!

Intuitiv kann man sich den Prozess der Erstellung einer Systemmatrix wie folgt vorstellen: Wir verbinden die Werte mit Federn, die wir erreichen wollen. In unserem Fall wollen wir zum Beispiel$$$x_i$ war gleich $$$x_{i+1}$ Also fügen wir die Gleichung hinzu $$$x_i - x_{i+1}=0$Zwischen diesen Werten hängt eine Feder, die sie zusammenzieht. Da die Werte von x0, x18 und x31 fest vorgegeben sind, bleibt nichts anderes übrig, als die Federn gleichmäßig zu dehnen, was (in diesem Fall) eine stückweise lineare Lösung ergibt.

Schreiben wir ein Programm, das dieses Gleichungssystem löst. Im letzten Artikel haben wir gesehen, dass die Gauß-Seidel-Methode sehr einfach zu programmieren ist, aber eine sehr langsame Konvergenz aufweist. Daher ist es besser, echte Löser von linearen Gleichungssystemen zu verwenden. Im einfachsten Fall sieht der Code für unser eindimensionales Beispiel so aus:

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # eliminate the constrained variables from the matrix A = A[:,[*range(1,18)] + [*range(19,31)]] b = np.matrix(np.zeros((n-1, 1))) b[0,0] = 1. b[17,0] = -2. b[18,0] = 2. b[n-2,0] = -1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] # re-introduce the constrained variables x.insert(0, 1.) x.insert(18, 2.) x.append(1.) 

Dieser Code erzeugt eine Liste x von 32 Elementen, in denen die Lösung gespeichert ist. Wir bauen eine Matrix$$$A$ Gebäude Vektor $$$b$ Wir erhalten einen Vektor mit einer Lösung $$$x = (A^\top A)^{-1}A^\top b$und dann fügen wir unsere festen Werte x0 = 1, x18 = 2 und x31 = 1 in diesen Vektor ein.

Dieser Code erledigt die notwendige Arbeit, aber es ist ziemlich unangenehm, die Werte fester Variablen auf die rechte Seite zu übertragen. Ist es möglich zu betrügen? Sie können! Schauen wir uns den folgenden Code an:

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1+3, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # enforce the constraints through the quadratic penalty A[n-1+0, 0] = 100. A[n-1+1,18] = 100. A[n-1+2,31] = 100. b = np.matrix(np.zeros((n-1+3, 1))) b[n-1+0,0] = 100.*1. b[n-1+1,0] = 100.*2. b[n-1+2,0] = 100.*1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] 

Aus Sicht eines Programmierers ist es viel schöner, der Vektor x wird sofort in der erforderlichen Dimension erhalten, und die Matrizen A und b werden viel einfacher ausgefüllt. Aber was ist der Trick? Schreiben wir das Gleichungssystem, das wir lösen:



Schauen Sie sich die letzten drei Gleichungen genau an:
100 x0 = 100 * 1
100 x18 = 100 * 2
100 x31 = 100 * 1

Könnte es einfacher sein, sie wie folgt zu schreiben?
x0 = 1
x18 = 2
x31 = 1

Nein, nicht einfacher. Wie ich bereits sagte, hängt jede Gleichung Federn, in diesem Fall die Feder zwischen x0 und Wert 1, die Feder zwischen x18 und Wert 2, und schließlich wird auch die Variable x31 zur Einheit hingezogen.

Aber der Koeffizient von 100 ist aus einem Grund da. Wir erinnern uns, dass dieses System einfach nicht gelöst werden kann, wir lösen es im Sinne der kleinsten Quadrate und minimieren die entsprechende quadratische Funktion. Multipliziert man die Koeffizienten der letzten drei Gleichungen mit jeweils 100, führt man eine Strafe ein, wenn man von den gewünschten Werten x0, x18 und x32 abweicht, die zehntausendmal (100 ^ 2) größer ist als die Strafe, wenn man von der Gleichheit abweicht$$$x_i = x_{i+1}$ .Grob gesagt sind die Federn der letzten drei Gleichungen zehntausendmal härter als bei allen anderen. Diese quadratische Strafmethode ist ein sehr praktisches Werkzeug für die Einführung von Beschränkungen, sie ist viel einfacher (wenn auch nicht ohne Nachteile) als das Reduzieren eines Satzes von Variablen.

Beispiel zwei, dreidimensional

Gehen wir zu etwas Interessanterem über, als die Elemente eines eindimensionalen Arrays zu glätten! Zunächst werden wir genau das Gleiche tun, jedoch mit interessanteren Daten und echten Tools. Ich möchte eine dreidimensionale Oberfläche nehmen, ihren Rand fixieren und den Rest der Oberfläche so gut wie möglich glätten:



Der Code ist hier verfügbar , aber nur für den Fall, dass ich eine vollständige Auflistung der Hauptdatei geben werde:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

Ich habe den einfachsten Parser für Wavefront-OBJ-Dateien geschrieben, sodass das Modell in einer Zeile geladen wird. Als Löser werde ich OpenNL verwenden, es ist ein sehr leistungsfähiger Löser für Probleme mit kleinsten Quadraten mit spärlichen Matrizen. Bitte beachten Sie, dass die Abmessungen der Matrizen gigantisch sein können: Wenn wir beispielsweise ein Schwarzweißbild mit einer Größe von 1000 x 1000 Pixel erhalten möchten, dann die Matrix$$$A^\top A$Wir werden eine Million pro Million haben! In der Praxis ist jedoch die überwiegende Mehrheit der Elemente dieser Matrix häufig Null, sodass alles nicht so beängstigend ist, Sie aber dennoch spezielle Löser verwenden müssen.

Schauen wir uns also den Code an. Zu Beginn kündige ich dem Löser an, was ich tun möchte:

  nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); 

Ich möchte eine Matrix haben $$$A^\top A$Größe (Anzahl der Eckpunkte) x (Anzahl der Eckpunkte). Achtung, wir geben dem Solver eine Matrix$$$A$ und $$$A^\top A$er wird es selbst bauen, was sehr praktisch ist! Achten Sie auch darauf, dass ich nicht ein Gleichungssystem löse, sondern drei in Reihe für x, y und z (ich habe gelogen, dass das Problem dreidimensional ist, es ist immer noch eindimensional!)

Und dann erkläre ich Zeile für Zeile unserer Matrix. Zunächst fixiere ich die Eckpunkte, die sich am Rand der Oberfläche befinden:

  for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } 

Sie können sehen, dass ich eine quadratische Strafe von 100 ^ 2 verwende, um die Kantenscheitelpunkte zu fixieren.

Nun, dann hänge ich für jedes Paar benachbarter Eckpunkte eine Feder der Steifheit 1 dazwischen:

  for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } 

Wir führen den Code aus und sehen, wie das Gesicht auf einem gebogenen Draht in die Oberfläche des Seifenfilms geglättet wird. Wir haben gerade das Dirichlet-Problem gelöst, indem wir eine Oberfläche mit minimaler Fläche erhalten haben.

Wir verbessern die Eigenschaften

Lassen Sie uns unser Gesicht in eine groteske Maske verwandeln:



Im vorherigen Artikel habe ich bereits gezeigt, wie dies am Knie gemacht wird.

  for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } 

Den vollständigen Code finden Sie hier . Wie arbeitet er? Wie im vorherigen Beispiel beginne ich mit dem Fixieren der Kantenscheitelpunkte. Dann sage ich für jede Kante (leise, mit einem Koeffizienten von 0,2), dass es schön wäre, wenn sie genau die gleiche Form hätte wie auf der ursprünglichen Oberfläche:

  for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } 

Wenn Sie nichts anderes tun und das Problem so lösen, wie es ist, sollten wir am Ausgang genau das ermitteln, was am Ausgang ausgegeben wurde: Die Ausgabegrenze entspricht der Eingabegrenze, und die Unterschiede am Ausgang entsprechen den Unterschieden am Eingang.

Aber wir werden dort nicht aufhören!

  for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } 

Ich füge unserem System weitere Gleichungen hinzu. Für jeden Eckpunkt zähle ich die Krümmung der ihn umgebenden Fläche in der Eingabefläche und multipliziere sie mit zweieinhalb, dh die Ausgabefläche sollte überall eine große Krümmung haben.

Dann rufen wir unseren Löser und erhalten eine gute Karikatur.

Letztes Beispiel für heute

Bis zu diesem Moment haben wir kein einziges neues Beispiel gesehen, alles wurde bereits im vorherigen Artikel gezeigt. Versuchen wir, etwas zu tun, das weniger trivial ist als die einfachste Glättung, die leicht ohne Verwendung von Lösungsmitteln erzielt werden kann. Der Code ist hier verfügbar , aber ich gebe Ihnen eine Auflistung:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" const Vec3f axes[] = {Vec3f(1,0,0), Vec3f(-1,0,0), Vec3f(0,1,0), Vec3f(0,-1,0), Vec3f(0,0,1), Vec3f(0,0,-1)}; int snap(Vec3f n) { // returns the coordinate axis closest to the given normal double nmin = -2.0; int imin = -1; for (int i=0; i<6; i++) { double t = n*axes[i]; if (t>nmin) { nmin = t; imin = i; } } return imin; } int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); std::vector<int> nearest_axis(m.nfaces()); for (int i=0; i<m.nfaces(); i++) { Vec3f v[3]; for (int j=0; j<3; j++) v[j] = m.point(m.vert(i, j)); Vec3f n = cross(v[1]-v[0], v[2]-v[0]).normalize(); nearest_axis[i] = snap(n); } for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); int axis = nearest_axis[i/3]/2; if (d!=axis) continue; nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

Wir arbeiten immer noch auf der gleichen Oberfläche wie zuvor. Wir nennen die Funktion snap () für jedes Dreieck. Diese Funktion gibt an, welche Achse des Koordinatensystems der Normalen dieses Dreiecks am nächsten liegt. Das heißt, wir möchten wissen, dass dieses Dreieck eher vertikal oder horizontal ist. Nun, dann wollen wir die Geometrie unserer Oberfläche ändern, damit das, was der Horizontalen nahe kommt, noch näher kommt! Der linke Teil dieses Bildes zeigt das Ergebnis der Funktion snap ():



Also haben wir unsere Oberfläche in drei Farben gemalt, die den drei Achsen des Koordinatensystems entsprechen. Nun, dann fügen wir für jede Kante unseres Systems die folgenden Gleichungen hinzu:

  nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); 

Das heißt, wir weisen jede Kante der Ausgangsfläche an, der entsprechenden Kante der Eingangsfläche, der Federsteifigkeit 1, zu ähneln. Wenn wir beispielsweise die Abmessung x zulassen und die Kante vertikal sein soll, sagen wir einfach, dass ein Scheitelpunkt mit der Federsteifigkeit dem anderen Scheitelpunkt gleich ist 2:

  nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); 

Nun, hier ist das Ergebnis unseres Programms: Eine



völlig vernünftige Frage: Idole von der Osterinsel, das ist natürlich cool, aber was hat Geologie damit zu tun? Gibt es Beispiele für echte Probleme?

Ja natürlich.Nehmen wir einen Abschnitt der Erdkruste:



Für Geologen sind Schichten verschiedener Gesteine ​​sehr wichtig, deren Grenzen (Horizonte) grün und die geologischen Verwerfungen rot dargestellt sind. Wir haben am Eingang ein Gitter aus Dreiecken (Tetraedern in 3D) der Region, die uns interessiert, aber Quads (Hexaeder in 3D) werden benötigt, um bestimmte Prozesse zu modellieren. Wir deformieren unser Modell so, dass die Fehler vertikal und die Horizonte (überraschend) horizontal werden:



Dann nehmen wir einfach ein regelmäßiges Quadratgitter, schneiden unsere Domäne in einheitliche Quadrate und wenden die inverse Transformation auf sie an, um das erforderliche Quadraster zu erhalten.

Fazit

Least-Square-Methoden sind ein leistungsfähiges Datenverarbeitungswerkzeug und werden in Excel-Spalten viel häufiger verwendet als Statistiken. Diese Möglichkeiten eröffnen sich uns aufgrund der Tatsache, dass die Minimierung einer quadratischen Funktion und die Lösung eines linearen Gleichungssystems ein und dasselbe sind, und wir (die Menschheit) haben gelernt, lineare Gleichungen sehr, sehr gut zu lösen, selbst wenn sie völlig unmenschliche Größen mit Milliarden von Variablen haben.

Es kann jedoch vorkommen, dass wir nicht genügend lineare Modelle haben. Und hier können beispielsweise neuronale Netze Abhilfe schaffen. Im nächsten Artikel werde ich versuchen zu zeigen, dass OLS mit Ablehnung von Emissionen einer der Formulierungen neuronaler Netze entspricht. Bleiben Sie auf dem Laufenden!