Verständliches RayTracing in 256 Zeilen C ++
Dies ist ein weiteres Kapitel aus meinem kurzen Kurs über Computergrafik . Dieses Mal sprechen wir über das Raytracing. Wie üblich versuche ich, Bibliotheken von Drittanbietern zu meiden, da ich glaube, dass die Schüler so überprüfen können, was unter der Haube vor sich geht. Überprüfen Sie auch das tinykaboom-Projekt .
Es gibt viele Raytracing-Artikel im Internet. Das Problem ist jedoch, dass fast alle von ihnen fertige Software zeigen, die sehr schwer zu verstehen sein kann. Nehmen Sie zum Beispiel die berühmte Business-Card-Ray-Tracer- Herausforderung. Es produziert sehr beeindruckende Programme, aber es ist sehr schwer zu verstehen, wie das funktioniert. Anstatt zu zeigen, dass ich Rendern kann, möchte ich Ihnen ausführlich erklären, wie Sie es selbst tun können.
Hinweis: Es macht keinen Sinn, nur meinen Code anzusehen oder diesen Artikel mit einer Tasse Tee in der Hand zu lesen. Dieser Artikel wurde entwickelt, damit Sie die Tastatur einnehmen und Ihre eigene Rendering-Engine implementieren können. Es wird sicherlich besser sein als meins. Zumindest die Programmiersprache ändern!
Das heutige Ziel ist es also zu lernen, wie man solche Bilder rendert:

Schritt 1: Schreiben Sie ein Image auf die Festplatte
Ich möchte mich nicht mit Fenstermanagern, Maus- / Tastaturverarbeitung und dergleichen beschäftigen. Das Ergebnis unseres Programms ist ein einfaches Bild, das auf der Festplatte gespeichert wird. Das erste, was wir tun müssen, ist, das Bild auf der Festplatte zu speichern. Hier finden Sie den Code, mit dem wir dies tun können. Lassen Sie mich die Hauptdatei auflisten:
#include <limits> #include <cmath> #include <iostream> #include <fstream> #include <vector> #include "geometry.h" void render() { const int width = 1024; const int height = 768; std::vector<Vec3f> framebuffer(width*height); for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } } std::ofstream ofs; // save the framebuffer to file ofs.open("./out.ppm"); ofs << "P6\n" << width << " " << height << "\n255\n"; for (size_t i = 0; i < height*width; ++i) { for (size_t j = 0; j<3; j++) { ofs << (char)(255 * std::max(0.f, std::min(1.f, framebuffer[i][j]))); } } ofs.close(); } int main() { render(); return 0; }
Nur render () wird in der Hauptfunktion aufgerufen und sonst nichts. Was steckt in der render () Funktion? Zunächst definiere ich den Framebuffer als eindimensionales Array von Vec3f-Werten. Dies sind einfache dreidimensionale Vektoren, die uns (r, g, b) Werte für jedes Pixel geben. Die Vektorklasse lebt in der Datei geometry.h, ich werde sie hier nicht beschreiben: Es ist wirklich eine triviale Manipulation von zwei- und dreidimensionalen Vektoren (Addition, Subtraktion, Zuordnung, Multiplikation mit einem Skalar, Skalarprodukt).
Ich speichere das Bild im ppm-Format . Dies ist der einfachste Weg, um Bilder zu speichern, aber nicht immer der bequemste, um sie weiter anzuzeigen. Wenn Sie in anderen Formaten speichern möchten, empfehlen wir Ihnen, eine Bibliothek eines Drittanbieters wie stb zu verknüpfen . Dies ist eine großartige Bibliothek: Sie müssen nur eine Header-Datei stb_image_write.h in das Projekt aufnehmen und können Bilder in den gängigsten Formaten speichern.
Warnung: Mein Code ist voller Fehler. Ich behebe sie im Upstream, ältere Commits sind jedoch betroffen. Überprüfen Sie dieses Problem .
Das Ziel dieses Schritts ist es also sicherzustellen, dass wir a) ein Bild im Speicher erstellen + verschiedene Farben zuweisen und b) das Ergebnis auf der Festplatte speichern können. Dann können Sie es in einer Software eines Drittanbieters anzeigen. Hier ist das Ergebnis:

Schritt 2, der entscheidende: Raytracing
Dies ist der wichtigste und schwierigste Schritt der gesamten Kette. Ich möchte eine Kugel in meinem Code definieren und zeichnen, ohne von Materialien oder Beleuchtung besessen zu sein. So sollte unser Ergebnis aussehen:

Der Einfachheit halber habe ich ein Commit pro Schritt in meinem Repository. Mit Github ist es sehr einfach, die vorgenommenen Änderungen anzuzeigen. Hier zum Beispiel , was sich durch das zweite Commit geändert hat.
Was brauchen wir, um die Kugel im Speicher des Computers darzustellen? Vier Zahlen reichen aus: Ein dreidimensionaler Vektor für den Mittelpunkt der Kugel und ein Skalar, der den Radius beschreibt:
struct Sphere { Vec3f center; float radius; Sphere(const Vec3f &c, const float &r) : center(c), radius(r) {} bool ray_intersect(const Vec3f &orig, const Vec3f &dir, float &t0) const { Vec3f L = center - orig; float tca = L*dir; float d2 = L*L - tca*tca; if (d2 > radius*radius) return false; float thc = sqrtf(radius*radius - d2); t0 = tca - thc; float t1 = tca + thc; if (t0 < 0) t0 = t1; if (t0 < 0) return false; return true; } };
Das einzige, was in diesem Code nicht trivial ist, ist eine Funktion, mit der Sie überprüfen können, ob ein gegebener Strahl (der von orig in Richtung dir stammt) unsere Kugel schneidet. Eine detaillierte Beschreibung des Algorithmus für die Strahl-Kugel-Schnittmenge finden Sie hier . Ich empfehle Ihnen dringend, dies zu tun und meinen Code zu überprüfen.
Wie funktioniert das Raytracing? Das ist ziemlich einfach. Im ersten Schritt haben wir das Bild mit einem Farbverlauf gefüllt:
for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } }
Jetzt formen wir für jedes Pixel einen Strahl, der vom Ursprung kommt und durch unser Pixel geht, und prüfen dann, ob dieser Strahl die Kugel schneidet:

Wenn es keinen Schnittpunkt mit einer Kugel gibt, zeichnen wir das Pixel mit color1, ansonsten mit color2:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { float sphere_dist = std::numeric_limits<float>::max(); if (!sphere.ray_intersect(orig, dir, sphere_dist)) { return Vec3f(0.2, 0.7, 0.8);
An dieser Stelle empfehle ich Ihnen, einen Bleistift zu nehmen und alle Berechnungen (den Schnittpunkt der Strahlenkugeln und das Überstreichen des Bildes mit den Strahlen) auf Papier zu überprüfen. Nur für den Fall, unsere Kamera wird von den folgenden Dingen bestimmt:
- Bildbreite
- Bildhöhe
- Sichtfeldwinkel
- Kamerastandort, Vec3f (0.0.0)
- Blickrichtung entlang der z-Achse in Richtung minus unendlich
Lassen Sie mich veranschaulichen, wie wir die Anfangsrichtung des zu verfolgenden Strahls berechnen. In der Hauptschleife haben wir diese Formel:
float x = (2*(i + 0.5)/(float)width - 1)*tan(fov/2.)*width/(float)height; float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.);
Woher kommt es? Ziemlich einfach. Unsere Kamera befindet sich im Ursprung und zeigt in Richtung -z. Lassen Sie mich das Zeug veranschaulichen, dieses Bild zeigt die Kamera von oben, die y-Achse zeigt aus dem Bildschirm:
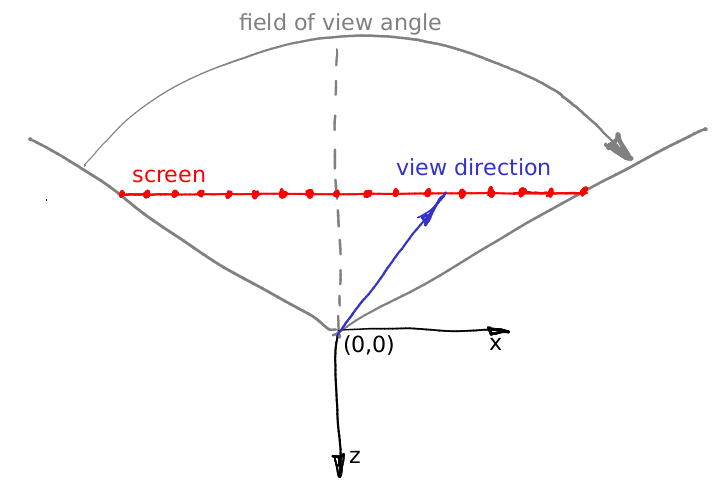
Wie gesagt, die Kamera befindet sich im Ursprung und die Szene wird auf die Leinwand projiziert, die in der Ebene z = -1 liegt. Das Sichtfeld gibt an, welcher Bereich des Raums auf dem Bildschirm sichtbar ist. In unserem Bild ist der Bildschirm 16 Pixel breit; Kannst du seine Länge in Weltkoordinaten berechnen? Es ist ganz einfach: Konzentrieren wir uns auf das Dreieck aus roter, grauer und grauer gestrichelter Linie. Es ist leicht zu erkennen, dass Bräune (Sichtfeld / 2) = (Bildschirmbreite) 0,5 / (Bildschirm-Kamera-Abstand). Wir platzieren den Bildschirm in einem Abstand von 1 zur Kamera, also (Bildschirmbreite) = 2 tan (Sichtfeld / 2).
Nehmen wir nun an, wir wollen einen Vektor durch die Mitte des 12. Pixels des Bildschirms werfen, dh wir wollen den blauen Vektor berechnen. Wie können wir das machen? Wie groß ist der Abstand vom linken Bildschirmrand bis zur Spitze des blauen Vektors? Erstens sind es 12 + 0,5 Pixel. Wir wissen, dass 16 Pixel des Bildschirms 2 tan (fov / 2) Welteinheiten entsprechen . Somit befindet sich die Spitze des Vektors bei (12 + 0,5) / 16 2 tan (fov / 2) Welteinheiten vom linken Rand oder im Abstand von (12 + 0,5) 2/16 * tan (fov / 2). - tan (fov / 2) vom Schnittpunkt zwischen dem Bildschirm und der -z-Achse. Wenn Sie das Bildschirmseitenverhältnis zu den Berechnungen hinzufügen, werden Sie genau die Formeln für die Strahlrichtung finden.
Schritt 3: Weitere Kugeln hinzufügen
Der schwierigste Teil ist vorbei, und jetzt ist unser Weg frei. Wenn wir wissen, wie man eine Kugel zeichnet, brauchen wir nicht lange, um ein paar mehr hinzuzufügen. Überprüfen Sie die Änderungen im Code, und dies ist das resultierende Bild:

Schritt 4: Beleuchtung
Das Bild ist in jeder Hinsicht perfekt, bis auf den Lichtmangel. Im Rest des Artikels werden wir über Beleuchtung sprechen. Fügen wir einige Punktlichtquellen hinzu:
struct Light { Light(const Vec3f &p, const float &i) : position(p), intensity(i) {} Vec3f position; float intensity; };
Die Berechnung der realen globalen Beleuchtung ist eine sehr, sehr schwierige Aufgabe. Daher werden wir wie alle anderen das Auge täuschen, indem wir völlig unkörperliche, aber visuell plausible Ergebnisse erzielen. Zunächst einmal: Warum ist es im Winter kalt und im Sommer heiß? Denn die Erwärmung der Erdoberfläche hängt vom Einfallswinkel der Sonnenstrahlen ab. Je höher die Sonne über dem Horizont steht, desto heller ist die Oberfläche. Umgekehrt ist es umso dunkler, je tiefer es sich über dem Horizont befindet. Und nachdem die Sonne über dem Horizont untergegangen ist, erreichen uns die Photonen überhaupt nicht mehr.
Zurück zu unseren Kugeln: Wir senden einen Strahl aus der Kamera aus (keine Beziehung zu Photonen!). Dabei bleibt er bei einer Kugel stehen. Woher kennen wir die Intensität der Schnittpunktbeleuchtung? Tatsächlich reicht es aus, den Winkel zwischen einem Normalenvektor an diesem Punkt und dem Vektor, der eine Lichtrichtung beschreibt, zu überprüfen. Je kleiner der Winkel, desto besser wird die Oberfläche beleuchtet. Man erinnere sich, dass das Skalarprodukt zwischen zwei Vektoren a und b gleich dem Produkt aus Vektornormen und dem Cosinus des Winkels zwischen den Vektoren ist: a * b = | a | | b | cos (alpha (a, b)). Wenn wir Vektoren mit Einheitslänge nehmen, gibt das Punktprodukt die Intensität der Oberflächenbeleuchtung an.
Daher geben wir in der cast_ray-Funktion anstelle einer konstanten Farbe die Farbe unter Berücksichtigung der Lichtquellen zurück:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { [...] float diffuse_light_intensity = 0; for (size_t i=0; i<lights.size(); i++) { Vec3f light_dir = (lights[i].position - point).normalize(); diffuse_light_intensity += lights[i].intensity * std::max(0.f, light_dir*N); } return material.diffuse_color * diffuse_light_intensity; }
Die Änderungen für den vorherigen Schritt sind hier verfügbar , und hier ist das Ergebnis:

Schritt 5: Spiegelbeleuchtung
Der Punktprodukt-Trick gibt eine gute Annäherung an die Ausleuchtung matter Oberflächen, in der Literatur heißt er diffuse Ausleuchtung. Was sollen wir tun, wenn wir glänzende Oberflächen zeichnen wollen? Ich möchte ein Bild wie dieses bekommen:

Prüfen Sie, wie wenig Änderungen notwendig waren. Kurz gesagt, je heller das Licht auf den glänzenden Oberflächen ist, desto geringer ist der Winkel zwischen der Blickrichtung und der Richtung des reflektierten Lichts.
Dieser Trick mit der Beleuchtung von matten und glänzenden Oberflächen ist als Phong-Reflexionsmodell bekannt . Das Wiki enthält eine ziemlich detaillierte Beschreibung dieses Beleuchtungsmodells. Es kann schön sein, es neben dem Quellcode zu lesen. Hier ist das Schlüsselbild zum Verständnis der Magie:

Schritt 6: Schatten
Warum haben wir das Licht, aber keine Schatten? Es ist nicht in Ordnung! Ich möchte dieses Bild:

Mit nur sechs Codezeilen können wir dies erreichen: Wenn wir jeden Punkt zeichnen, achten wir nur darauf, dass das Segment zwischen dem aktuellen Punkt und der Lichtquelle die Objekte unserer Szene nicht schneidet. Wenn es eine Kreuzung gibt, überspringen wir die aktuelle Lichtquelle. Es gibt nur eine kleine Subtilität: Ich störe den Punkt, indem ich ihn in die Richtung des Normalen bewege:
Vec3f shadow_orig = light_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
Warum ist das so? Es ist nur so, dass unser Punkt auf der Oberfläche des Objekts liegt und (mit Ausnahme der Frage der numerischen Fehler) jeder Strahl von diesem Punkt das Objekt selbst schneidet.
Schritt 7: Reflexionen
Es ist unglaublich, aber um Reflexionen zu unserem Render hinzuzufügen, müssen wir nur drei Codezeilen hinzufügen:
Vec3f reflect_dir = reflect(dir, N).normalize(); Vec3f reflect_orig = reflect_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
Überzeugen Sie sich selbst: Beim Durchschneiden der Kugel berechnen wir einfach den reflektierten Strahl (mit Hilfe derselben Funktion, die wir für Glanzlichter verwendet haben!) Und rufen die cast_ray-Funktion rekursiv in Richtung des reflektierten Strahls auf. Stelle sicher, dass du mit der Rekursionstiefe spielst, ich setze sie auf 4, versuche verschiedene Werte, die von 0 ausgehen. Was ändert sich im Bild? Hier ist mein Ergebnis mit Reflexionen und einer Rekursionstiefe von 4:

Schritt 8: Refraktionen
Wenn wir wissen, wie man reflektiert, sind Refraktionen einfach . Wir müssen eine Funktion zur Berechnung des gebrochenen Strahls (unter Verwendung des Snellschen Gesetzes ) und drei weitere Codezeilen in unserer rekursiven Funktion cast_ray hinzufügen. Hier ist das Ergebnis, wo die nächste Kugel "aus Glas" ist, sie reflektiert und bricht das Licht gleichzeitig:

Steo 9: Jenseits der Sphären
Bis zu diesem Moment haben wir nur Kugeln gerendert, weil es eines der einfachsten nichttrivialen mathematischen Objekte ist. Fügen wir ein Flugzeug hinzu. Das Schachbrett ist eine klassische Wahl. Für diesen Zweck ist es völlig ausreichend, ein Dutzend Zeilen hinzuzufügen.
Und hier ist das Ergebnis:

Wie versprochen enthält der Code 256 Codezeilen. Überzeugen Sie sich selbst !
Schritt 10: Hausaufgabe
Wir haben einen langen Weg zurückgelegt: Wir haben gelernt, wie man einer Szene Objekte hinzufügt, wie man eine ziemlich komplizierte Beleuchtung berechnet. Lassen Sie mich zwei Aufgaben als Hausaufgabe hinterlassen. Absolut alle Vorarbeiten wurden bereits in der Filiale Hausaufgabe erledigt. Für jede Zuweisung sind zehn Codezeilen erforderlich.
Aufgabe 1: Umgebungskarte
Im Moment, wenn der Strahl kein Objekt schneidet, setzen wir das Pixel einfach auf die konstante Hintergrundfarbe. Und warum ist es eigentlich konstant? Nehmen wir ein kugelförmiges Foto (Datei envmap.jpg ) und verwenden es als Hintergrund! Um das Leben einfacher zu machen, habe ich unser Projekt mit der stb-Bibliothek verknüpft, um die Arbeit mit dem jpg-Format zu vereinfachen. Es sollte uns ein solches Bild geben:

Aufgabe 2: Quacksalber!
Wir können sowohl Kugeln als auch Ebenen rendern (siehe Schachbrett). Zeichnen wir also Dreiecksnetze! Ich habe einen Code geschrieben, mit dem Sie eine OBJ-Datei lesen können, und ich habe ihm eine Funktion zum Schneiden von Strahlendreiecken hinzugefügt. Jetzt sollte es ganz einfach sein, die Ente zu unserer Szene hinzuzufügen:

Fazit
Mein Hauptziel ist es, Projekte zu zeigen, die interessant (und einfach!) Zu programmieren sind. Ich bin überzeugt, dass man viele Nebenprojekte machen muss, um ein guter Programmierer zu werden. Ich weiß nichts über Sie, aber ich persönlich bin nicht angetan von Buchhaltungssoftware und dem Minensuchspiel, auch wenn die Komplexität des Codes durchaus vergleichbar ist.
Ein paar Stunden und zweihundertfünfzig Zeilen Code geben uns einen Raytracer. Fünfhundert Zeilen des Software-Rasters können in wenigen Tagen erstellt werden. Grafik ist wirklich cool, um die Programmierung zu lernen!