
Im Oktober fand die zweite Programmiermeisterschaft statt. Wir haben 12.500 Bewerbungen erhalten, mehr als 6.000 Menschen haben sich bei Wettbewerben versucht. Diesmal konnten die Teilnehmer einen der folgenden Tracks auswählen: Backend, Frontend, Mobile Development und Machine Learning. In jeder Strecke war es erforderlich, die Qualifikationsphase und das Finale zu bestehen.
Aus Tradition veröffentlichen wir eine Analyse der Tracks auf Habré. Beginnen wir mit den Aufgaben der Qualifizierungsphase des maschinellen Lernens. Das Team bereitete fünf solcher Aufgaben vor, von denen es zwei Optionen für drei Aufgaben gab: In der ersten Version gab es Aufgaben A1, B1 und C, in der zweiten - A2, B2 und C. Die Optionen wurden zufällig unter den Teilnehmern verteilt. Der Autor von Aufgabe C ist unser Entwickler Pavel Parkhomenko, die restlichen Aufgaben hat sein Kollege Nikita Senderovich übernommen.
Für die erste einfache algorithmische Aufgabe (A1 / A2) konnten die Teilnehmer 50 Punkte erhalten, indem sie die Antwort korrekt aufzählten. Für die zweite Aufgabe (B1 / B2) gaben wir 10 bis 100 Punkte - je nach Wirksamkeit der Lösung. Um 100 Punkte zu erzielen, musste die dynamische Programmiermethode implementiert werden. Die dritte Aufgabe bestand in der Erstellung eines Klickmodells auf der Grundlage der bereitgestellten Trainingsdaten. Es erforderte die Anwendung von Methoden zum Arbeiten mit kategorialen Attributen und die Verwendung eines nichtlinearen Lernmodells (z. B. Gradientenerhöhung). Für die Aufgabe konnten - abhängig vom Wert der Verlustfunktion auf dem Prüfling - bis zu 150 Punkte erreicht werden.
A1. Stellen Sie die Länge des Karussells wieder her
Zustand
Das Empfehlungssystem sollte die Interessen der Menschen effektiv bestimmen. Zusätzlich zu den Methoden des maschinellen Lernens werden für diese Aufgabe spezielle Schnittstellenlösungen verwendet, die den Benutzer explizit fragen, was ihn interessiert. Eine solche Lösung ist das Karussell.
Ein Karussell ist ein horizontales Kartenband, in dem jeweils eine bestimmte Quelle oder ein bestimmtes Thema abonniert werden kann. Dieselbe Karte befindet sich mehrmals im Karussell. Das Karussell kann von links nach rechts gescrollt werden, während der Benutzer nach der letzten Karte wieder die erste sieht. Für den Benutzer ist der Übergang von der letzten zur ersten Karte unsichtbar, aus seiner Sicht ist das Band endlos.
Irgendwann bemerkte ein neugieriger Benutzer, dass das Band tatsächlich geloopt war, und beschloss, die wahre Länge des Karussells herauszufinden. Zu diesem Zweck begann er, durch das Band zu scrollen und der Einfachheit halber nacheinander die Besprechungskarten zu schreiben, wobei jede Karte mit einem lateinischen Kleinbuchstaben gekennzeichnet wurde. Also schrieb Wassili die ersten n Karten auf ein Stück Papier. Es ist garantiert, dass er alle Karussellkarten mindestens einmal angeschaut hat. Dann ging Vasily ins Bett, und am Morgen stellte er fest, dass jemand ein Glas Wasser auf seine Notizen geschüttet hatte und nun einige Buchstaben nicht mehr erkannt werden konnten.
Helfen Sie Vasily nach den verbleibenden Informationen dabei, die kleinstmögliche Anzahl von Karten im Karussell zu ermitteln.
E / A-Formate und BeispieleEingabeformat
Die erste Zeile enthält eine einzelne Ganzzahl n (1 ≤ n ≤ 1000) - die Anzahl der von Vasily geschriebenen Zeichen.
Die zweite Zeile enthält die von Vasily geschriebene Sequenz. Es besteht aus n Zeichen - lateinische Kleinbuchstaben und das # -Zeichen, was bedeutet, dass der Buchstabe an dieser Position nicht erkannt werden kann.
Ausgabeformat
Drucken Sie eine einzelne positive Ganzzahl - die kleinstmögliche Anzahl von Karten im Karussell.
Beispiel 1
Beispiel 2
Beispiel 3
Beispiel 4
Hinweise
Im ersten Beispiel wurden alle Buchstaben erkannt, das minimale Karussell konnte aus 3 Karten bestehen - abc.
Im zweiten Beispiel wurden alle Buchstaben erkannt, das Mindestkarussell könnte aus 3 Karten bestehen - abb. Bitte beachten Sie, dass die zweite und dritte Karte in diesem Karussell identisch sind.
Im dritten Beispiel wird die kleinstmögliche Karusselllänge erhalten, wenn angenommen wird, dass sich das Symbol a an der dritten Position befand. Dann ist die Anfangszeile abeba, das minimale Karussell besteht aus 2 Karten - ab.
Im vierten Beispiel könnte die Quellzeichenfolge alles sein, zum Beispiel ffffff. Dann könnte das Karussell aus einer Karte bestehen - f.
Bewertungssystem
Erst wenn Sie alle Tests für die Aufgabe bestanden haben, erhalten Sie
50 Punkte .
Im Testsystem sind die Tests 1–4 Beispiele für die Bedingung.
Lösung
Es reichte aus, die mögliche Länge des Karussells von 1 bis n zu sortieren und für jede feste Länge zu prüfen, ob dies möglich ist. Es ist klar, dass die Antwort immer existiert, da der Wert von n garantiert eine mögliche Antwort ist. Für eine feste Karusselllänge p genügt es zu überprüfen, dass in der übertragenen Leitung für alle i von 0 bis (p - 1) an allen Positionen i, i + p, i + 2p usw. die gleichen Zeichen oder # gefunden werden. Wenn es zumindest für einige i 2 verschiedene Zeichen aus dem Bereich von a bis z gibt, kann das Karussell nicht die Länge p haben. Da Sie im schlimmsten Fall für jedes p alle Zeichen des Strings einmal durchlaufen müssen, ist die Komplexität dieses Algorithmus O (n
2 ).
def check_character(char, curchar): return curchar is None or char == "#" or curchar == char def need_to_assign_curchar(char, curchar): return curchar is None and char != "#" n = int(input()) s = input().strip() for p in range(1, n + 1): is_ok = True for i in range(0, p): curchar = None for j in range(i, n, p): if not check_character(s[j], curchar): is_ok = False break if need_to_assign_curchar(s[j], curchar): curchar = s[j] if not is_ok: break if is_ok: print(p) break
A2. Stellen Sie die Länge des Karussells wieder her
Zustand
Das Empfehlungssystem sollte die Interessen der Menschen effektiv bestimmen. Zusätzlich zu den Methoden des maschinellen Lernens werden für diese Aufgabe spezielle Schnittstellenlösungen verwendet, die den Benutzer explizit fragen, was ihn interessiert. Eine solche Lösung ist das Karussell.
Ein Karussell ist ein horizontales Kartenband, in dem jeweils eine bestimmte Quelle oder ein bestimmtes Thema abonniert werden kann. Dieselbe Karte befindet sich mehrmals im Karussell. Das Karussell kann von links nach rechts gescrollt werden, während der Benutzer nach der letzten Karte wieder die erste sieht. Für den Benutzer ist der Übergang von der letzten zur ersten Karte unsichtbar, aus seiner Sicht ist das Band endlos.
Irgendwann bemerkte ein neugieriger Benutzer, dass das Band tatsächlich geloopt war, und beschloss, die wahre Länge des Karussells herauszufinden. Zu diesem Zweck begann er, durch das Band zu scrollen und der Einfachheit halber nacheinander die Besprechungskarten zu schreiben, wobei jede Karte mit einem lateinischen Kleinbuchstaben gekennzeichnet wurde. Also schrieb Vasily die ersten n Karten aus. Es ist garantiert, dass er alle Karussellkarten mindestens einmal angeschaut hat. Da Wassili durch den Inhalt der Karten abgelenkt war, konnte er beim Schreiben fälschlicherweise einen Buchstaben durch einen anderen ersetzen, aber es ist bekannt, dass er insgesamt nicht mehr als k Fehler machte.
Die Aufnahmen von Vasily sind Ihnen in die Hände gefallen, Sie kennen auch den Wert von k. Bestimmen Sie, wie wenige Karten in seinem Karussell sein können.
E / A-Formate und BeispieleEingabeformat
Die erste Zeile enthält zwei Ganzzahlen: n (1 ≤ n ≤ 500) - die Anzahl der von Basil geschriebenen Zeichen und k (0 ≤ k ≤ n) - die maximale Anzahl der Fehler, die Vasily gemacht hat.
Die zweite Zeile enthält n Kleinbuchstaben des lateinischen Alphabets - die von Vasily geschriebene Sequenz.
Ausgabeformat
Drucken Sie eine einzelne positive Ganzzahl - die kleinstmögliche Anzahl von Karten im Karussell.
Beispiel 1
Beispiel 2
Beispiel 3
Beispiel 4
Hinweise
Im ersten Beispiel ist k = 0, und wir wissen mit Sicherheit, dass Vasily sich nicht getäuscht hat. Das minimale Karussell könnte aus 3 Karten bestehen - abc.
Im zweiten Beispiel wird die kleinstmögliche Karusselllänge erhalten, wenn wir annehmen, dass Vasily fälschlicherweise den dritten Buchstaben a durch c ersetzt hat. Dann ist die reale Linie abeba, das minimale Karussell besteht aus 2 Karten - ab.
Im dritten Beispiel ist bekannt, dass Vasily einen Fehler machen könnte. Die Größe des Karussells ist jedoch minimal, vorausgesetzt, er hat keine Fehler gemacht. Das minimale Karussell besteht aus 3 Karten - abb. Bitte beachten Sie, dass die zweite und dritte Karte in diesem Karussell identisch sind.
Im vierten Beispiel können wir sagen, dass Vasily sich bei der Eingabe aller Buchstaben getäuscht hat, und die ursprüngliche Zeile könnte tatsächlich eine beliebige sein, zum Beispiel ffffff. Dann könnte das Karussell aus einer Karte bestehen - f.
Bewertungssystem
Erst wenn Sie alle Tests für die Aufgabe bestanden haben, erhalten Sie
50 Punkte .
Im Testsystem sind die Tests 1–4 Beispiele für die Bedingung.
Lösung
Es reichte aus, die mögliche Länge des Karussells von 1 bis n zu sortieren und für jede feste Länge zu prüfen, ob dies möglich ist. Es ist klar, dass die Antwort immer existiert, da der Wert von n garantiert eine mögliche Antwort ist, unabhängig vom Wert von k. Für eine feste Karusselllänge p genügt es, unabhängig für alle i von 0 bis (p - 1) zu berechnen, wie viele Fehler mindestens an den Positionen i, i + p, i + 2p usw. gemacht wurden. Diese Anzahl von Fehlern ist minimal, wenn sie als wahr angenommen werden Das Symbol ist dasjenige, das an diesen Stellen am häufigsten vorkommt. Dann ist die Anzahl der Fehler gleich der Anzahl der Stellen, auf denen ein anderer Buchstabe steht. Wenn für einige p die Gesamtzahl der Fehler k nicht überschreitet, ist der Wert p eine mögliche Antwort. Da Sie für jedes p alle Zeichen des Strings einmal durchgehen müssen, ist die Komplexität dieses Algorithmus O (n
2 ).
n, k = map(int, input().split()) s = input().strip() for p in range(1, n + 1): mistakes = 0 for i in range(0, p): counts = [0] * 26 for j in range(i, n, p): counts[ord(s[j]) - ord("a")] += 1 mistakes += sum(counts) - max(counts) if mistakes <= k: print(p) break
B1. Optimales Empfehlungsband
Zustand
Die Bildung des nächsten Teils der persönlichen Abgabe von Empfehlungen für den Benutzer ist keine leichte Aufgabe. Berücksichtigen Sie n Veröffentlichungen, die auf der Grundlage der Auswahl der Kandidaten aus einer Empfehlungsbasis ausgewählt wurden. Publikationsnummer i ist gekennzeichnet durch eine Relevanzbewertung s
i und eine Menge von k binären Attributen a
i1 , a
i2 , ..., a
ik . Jedes dieser Attribute entspricht einer Eigenschaft der Publikation, z. B. ob der Benutzer die Quelle dieser Publikation abonniert hat, ob die Publikation in den letzten 24 Stunden erstellt wurde usw. Die Publikation kann mehrere dieser Eigenschaften gleichzeitig aufweisen. In diesem Fall nehmen die entsprechenden Attribute den Wert an 1, oder es kann keine von ihnen haben - und dann sind alle seine Attribute 0.
Damit der Feed des Benutzers vielfältig ist, müssen unter m Kandidaten n Veröffentlichungen ausgewählt werden, sodass unter ihnen mindestens A
1 Veröffentlichungen mit der ersten Eigenschaft, mindestens A
2 Veröffentlichungen mit der zweiten Eigenschaft, ..., A
k Veröffentlichungen mit der Eigenschaft von Nummer k. Ermitteln Sie den maximal möglichen Gesamtrelevanzwert für m Veröffentlichungen, die diese Anforderung erfüllen, oder stellen Sie fest, dass eine solche Reihe von Veröffentlichungen nicht vorhanden ist.
E / A-Formate und BeispieleEingabeformat
Die erste Zeile enthält drei ganze Zahlen - n, m, k (1 ≤ n ≤ 50, 1 ≤ m ≤ min (n, 9), 1 ≤ k ≤ 5).
Die nächsten n Zeilen zeigen die Merkmale von Veröffentlichungen. Die i-te Veröffentlichung erhält eine ganze Zahl s
i (1 ≤ s
i ≤ 10
9 ) - eine Bewertung der Relevanz dieser Veröffentlichung, und dann ist ein Leerzeichen von k Zeichen, von denen jedes 0 oder 1 ist, der Wert jedes der Attribute dieser Veröffentlichung.
Die letzte Zeile enthält k durch Leerzeichen getrennte Ganzzahlen - die Werte A
1 , ..., A
k (0 ≤ A
i ≤ m), die die Anforderungen für die endgültige Menge von m Veröffentlichungen definieren.
Ausgabeformat
Wenn es keinen Satz von m Veröffentlichungen gibt, die die Einschränkungen erfüllen, drucken Sie die Nummer 0. Anderenfalls drucken Sie eine einzelne positive Ganzzahl - die maximal mögliche Gesamtrelevanzbewertung.
Beispiel 1
Beispiel 2
Hinweise
Im ersten Beispiel sollten aus vier Veröffentlichungen mit zwei Eigenschaften zwei ausgewählt werden, sodass es mindestens eine Veröffentlichung mit der ersten Eigenschaft und eine mit der zweiten Eigenschaft gibt. Die größte Relevanz kann erhalten werden, wenn wir die zweite und dritte Veröffentlichung verwenden, obwohl jede Option mit einer vierten Veröffentlichung auch für Einschränkungen geeignet ist.
Im zweiten Beispiel ist es nicht möglich, zwei Veröffentlichungen auszuwählen, sodass beide die zweite Eigenschaft haben, da nur die erste Veröffentlichung über sie verfügt.
Bewertungssystem
Tests für diese Aufgabe bestehen aus fünf Gruppen. Punkte für jede Gruppe werden nur vergeben, wenn alle Tests der Gruppe und alle Tests der
vorherigen Gruppen bestanden wurden. Das Bestehen von Tests anhand der Bedingungen ist erforderlich, um Punkte für Gruppen zu erhalten, die mit der zweiten beginnen. Insgesamt können Sie für die Aufgabe
100 Punkte erhalten .
Im Testsystem sind die Tests 1-2 Beispiele für die Bedingung.
1.
(10 Punkte) Tests 3–10: k = 1, m ≤ 3, s
i ≤ 1000, es sind keine Tests für die Bedingung erforderlich
2.
(20 Punkte) Tests 11–20: k ≤ 2, m ≤ 3
3.
(20 Punkte) Tests 21–29: k ≤ 2
4.
(20 Punkte) Tests 30–37: k ≤ 3
5.
(30 Punkte) Tests 38–47: keine zusätzlichen Einschränkungen
Lösung
Es gibt n Publikationen, jede hat Geschwindigkeit und k Boolesche Flags, es ist notwendig, m Karten so auszuwählen, dass die Summe der Relevanzen maximal ist und k Anforderungen der Form „unter den ausgewählten m Publikationen muss ≥ A
i Karten mit dem i-ten Flag haben“ erfüllt sind, oder dies zu bestimmen Eine solche Reihe von Veröffentlichungen gibt es nicht.
Die Entscheidung liegt bei 10 Punkten : Wenn es genau ein Flag gibt, ist es ausreichend, A
1 -Publikationen mit diesem Flag zu nehmen, die am relevantesten sind (wenn es weniger solche Karten als A
1 gibt , dann existiert der gewünschte Satz nicht), und der Rest (m - A
1 ) wird von den übrigen aufgenommen Karten mit der besten Relevanz.
Die Lösung lautet 30 Punkte : Wenn m 3 nicht überschreitet, können Sie die Antwort durch erschöpfende Suche nach allen möglichen O (n
3 ) -Dreifachen von Karten finden. Wählen Sie die beste Option in Bezug auf die Gesamtrelevanz, die die Einschränkungen erfüllt.
Die Entscheidung liegt bei 70 Punkten (50 Punkte sind gleich, nur einfacher umzusetzen): Wenn es nicht mehr als 3 Flags gibt, können Sie alle Veröffentlichungen in 8 disjunkte Gruppen einteilen, je nachdem, wie viele Flags sie haben: 000, 001, 010, 011, 100, 101, 110, 111. Veröffentlichungen in jeder Gruppe sollten in absteigender Reihenfolge nach Relevanz sortiert werden. Dann können wir für O (m
4 ) herausfinden, wie viele der besten Veröffentlichungen wir aus den Gruppen 111, 011, 110 und 101 nehmen. Von jeder nehmen wir von 0 bis m Veröffentlichungen, insgesamt nicht mehr als m. Danach wird klar, wie viele Publikationen aus den Gruppen 100, 010 und 001 gesammelt werden müssen, um die Anforderungen zu erfüllen. Es bleibt zu m mit den verbleibenden Karten mit der besten Relevanz zu bekommen.
Komplettlösung : Betrachten Sie die dynamische Programmierfunktion dp [i] [a] ... [z]. Dies ist die maximale Gesamtrelevanzbewertung, die mit genau i Publikationen erhalten werden kann, so dass genau eine Publikation mit Flag A, ..., z Publikationen mit Flag Z vorliegt. Dann wird zunächst dp [0] [0] ... [0] = 0 und für alle anderen Parametersätze setzen wir den Wert gleich -1, um diesen Wert in Zukunft zu maximieren. Als nächstes werden wir nacheinander in das Spiel einsteigen und mit jeder Karte die Werte dieser Funktion verbessern: für jeden Dynamikzustand (i, a, b, ..., z) unter Verwendung der j-ten Veröffentlichung mit Flags (a
j , b)
j , ..., z
j ) können wir versuchen, in den Zustand überzugehen (i + 1, a + a
j , b + b
j , ..., z + z
j ) und prüfen, ob sich das Ergebnis in diesem Zustand verbessert. Wichtig: Während des Übergangs sind wir nicht an Zuständen interessiert, in denen i ≥ m ist, daher betragen die Gesamtzustände dieser Dynamik nicht mehr als m
k + 1 , und das resultierende asymptotische Verhalten ist O (nm
k + 1 ). Wenn die Dynamikzustände berechnet werden, ist die Antwort ein Zustand, der die Bedingungen erfüllt und die höchste Gesamtrelevanzbewertung ergibt.
Unter dem Gesichtspunkt der Implementierung ist es nützlich, den Status der dynamischen Programmierung und die Flags jeder Veröffentlichung in gepackter Form in einer ganzen Zahl zu speichern, um die Arbeit des Programms zu beschleunigen (siehe Code), und nicht in einer Liste oder einem Tupel. Diese Lösung benötigt weniger Speicher und ermöglicht es Ihnen, den Status der Dynamik effektiv zu aktualisieren.
Vollständiger Lösungscode:
def pack_state(num_items, counts): result = 0 for count in counts: result = (result << 8) + count return (result << 8) + num_items def get_num_items(state): return state & 255 def get_flags_counts(state, num_flags): flags_counts = [0] * num_flags state >>= 8 for i in range(num_flags): flags_counts[num_flags - i - 1] = state & 255 state >>= 8 return flags_counts n, m, k = map(int, input().split()) scores, attributes = [], [] for i in range(n): score, flags = input().split() scores.append(int(score)) attributes.append(list(map(int, flags))) limits = list(map(int, input().split())) dp = {0 : 0} for i in range(n): score = scores[i] state_delta = pack_state(1, attributes[i]) dp_temp = {} for state, value in dp.items(): if get_num_items(state) >= m: continue new_state = state + state_delta if value + score > dp.get(new_state, -1): dp_temp[new_state] = value + score dp.update(dp_temp) best_score = 0 for state, value in dp.items(): if get_num_items(state) != m: continue flags_counts = get_flags_counts(state, k) satisfied_bounds = True for i in range(k): if flags_counts[i] < limits[i]: satisfied_bounds = False break if not satisfied_bounds: continue if value > best_score: best_score = value print(best_score)
B2. Funktionsapproximation
Zustand
Zur Beurteilung der Relevanz von Dokumenten werden verschiedene Methoden des maschinellen Lernens eingesetzt - beispielsweise Entscheidungsbäume. Der k-fache Entscheidungsbaum hat in jedem Knoten eine Entscheidungsregel, die Objekte gemäß den Werten einiger Attribute in k Klassen unterteilt. In der Praxis werden üblicherweise binäre Entscheidungsbäume verwendet. Stellen Sie sich eine vereinfachte Version des Optimierungsproblems vor, die in jedem Knoten des k-ary-Entscheidungsbaums gelöst werden muss.
An den Punkten i = 1, 2, ..., n sei eine diskrete Funktion f definiert. Es ist notwendig, eine stückweise konstante Funktion g zu finden, die aus nicht mehr als k Konstanzabschnitten besteht, so dass der Wert SSE = ist
(g (i) - f (i))
2 ist minimal.
E / A-Formate und BeispieleEingabeformat
Die erste Zeile enthält zwei ganze Zahlen n und k (1 ≤ n ≤ 300, 1 ≤ k ≤ min (n, 10)).
Die zweite Zeile enthält n ganze Zahlen f (1), f (2), ..., f (n) - die Werte der Näherungsfunktion an den Punkten 1, 2, ..., n (–10
6 ≤ f (i) ≤ 10
6 ).
Ausgabeformat
Geben Sie eine einzelne Zahl aus - der minimal mögliche Wert von SSE. Die Antwort gilt als richtig, wenn der absolute oder relative Fehler 10
–6 nicht überschreitet.
Beispiel 1
Beispiel 2
Beispiel 3
Hinweise
Im ersten Beispiel ist die optimale Funktion g die Konstante g (i) = 2.
SSE = (2 - 1)
2 + (2 - 2)
2 + (2 - 3)
2 = 2.
Im zweiten Beispiel gibt es 2 Optionen. Entweder ist g (1) = 1 und g (2) = g (3) = 2,5 oder g (1) = g (2) = 1,5 und
g (3) = 3. In jedem Fall ist SSE = 0,5.
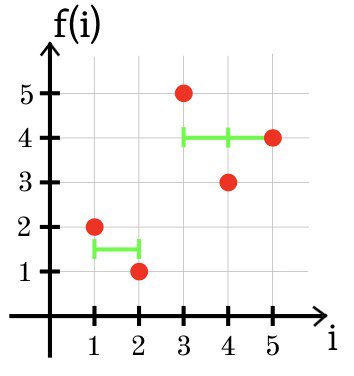
Im dritten Beispiel ist die optimale Approximation der Funktion f unter Verwendung von zwei Konstanzabschnitten unten gezeigt: g (1) = g (2) = 1,5 und g (3) = g (4) = g (5) = 4.
SSE = (1,5 + 2)
2 + (1,5 - 1)
2 + (4 - 5)
2 + (4 - 3)
2 + (4 - 4)
2 = 2,5.
Bewertungssystem
Tests für diese Aufgabe bestehen aus fünf Gruppen. Punkte für jede Gruppe werden nur vergeben, wenn alle Tests der Gruppe und alle Tests der
vorherigen Gruppen bestanden wurden. Das Bestehen von Tests anhand der Bedingungen ist erforderlich, um Punkte für Gruppen zu erhalten, die mit der zweiten beginnen. Insgesamt können Sie für die Aufgabe
100 Punkte erhalten .
Im Testsystem sind die Tests 1-3 Beispiele für die Bedingung.
1.
(10 Punkte) Tests 4–22: k = 1, es sind keine Tests für die Bedingung erforderlich
2.
(20 Punkte) Tests 23–28: k ≤ 2
3.
(20 Punkte) Tests 29–34: k ≤ 3
4.
(20 Punkte) Tests 35–40: k ≤ 4
5.
(30 Punkte) Tests 41–46: keine zusätzlichen Einschränkungen
Lösung
Wie Sie wissen, ist die Konstante, die den SSE-Wert für eine Menge von Werten f
1 , f
2 , ..., f
n minimiert, der Durchschnitt der hier aufgeführten Werte. Da es außerdem leicht ist, durch einfache Berechnungen zu verifizieren, ist der Wert SSE =
.
Die Entscheidung ist 10 Punkte : Wir betrachten einfach den Durchschnitt aller Werte der Funktion und SSE als O (n).
Die Entscheidung liegt bei 30 Punkten : Wir sortieren den letzten Punkt in Bezug auf den ersten Teil der Konstanz der beiden, für eine feste Partition berechnen wir den SSE und wählen den optimalen aus. Darüber hinaus ist es wichtig, nicht zu vergessen, das Gehäuse zu zerlegen, wenn es nur einen Konstanzbereich gibt. Schwierigkeit - O (n
2 ).
Die Entscheidung liegt bei 50 Punkten : Wir sortieren die Grenzen der Aufteilung in Konstanzabschnitte für O (n
2 ), für eine feste Aufteilung in 3 Segmente berechnen wir den SSE und wählen den optimalen aus. Schwierigkeit - O (n
3 ).
Die Entscheidung liegt bei 70 Punkten : Wir berechnen die Summe und die Summe der Quadrate der Werte von f
i für die Präfixe. Dadurch werden schnell der Durchschnitt und der SSE für jedes Segment berechnet. Wir sortieren die Grenzen der Partition in 4 Abschnitte der Konstanz für O (n
3 ), wobei wir die SSE anhand der vorberechneten Werte der Präfixe für O (1) berechnen. Schwierigkeit - O (n
3 ).
Komplettlösung : Betrachten Sie die dynamische Programmierfunktion dp [s] [i]. Dies ist der kleinste SSE-Wert, wenn wir die ersten i-Werte mit s-Segmenten approximieren. Dann
dp [0] [0] = 0, und für alle anderen Parametersätze setzen wir den Wert auf unendlich, um diesen Wert weiter zu minimieren. Wir werden das Problem lösen und den Wert von s schrittweise erhöhen. Wie berechnet man dp [s] [i], wenn die Dynamikwerte für alle kleineren s bereits berechnet wurden? Es ist ausreichend, für t die Anzahl der ersten Punkte zu bestimmen, die von den vorherigen (s - 1) Segmenten abgedeckt werden, und alle Werte von t zu sortieren und die verbleibenden (i - t) Punkte unter Verwendung des verbleibenden Segments zu approximieren. Es ist notwendig, den besten Wert t für die endgültige SSE bei i Punkten zu wählen. Wenn wir die Summen und Quadratsummen der Werte von fi auf den Präfixen berechnen, wird diese Approximation in O (1) durchgeführt, und der Wert dp [s] [i] kann in O (n) berechnet werden. Die endgültige Antwort lautet dp [k] [n]. Die Gesamtkomplexität des Algorithmus ist O (kn
2 ).
Vollständiger Lösungscode:
n, k = map(int, input().split()) f = list(map(float, input().split())) prefix_sum = [0.0] * (n + 1) prefix_sum_sqr = [0.0] * (n + 1) for i in range(1, n + 1): prefix_sum[i] = prefix_sum[i - 1] + f[i - 1] prefix_sum_sqr[i] = prefix_sum_sqr[i - 1] + f[i - 1] ** 2 def get_best_sse(l, r): num = r - l + 1 s_sqr = (prefix_sum[r] - prefix_sum[l - 1]) ** 2 ss = prefix_sum_sqr[r] - prefix_sum_sqr[l - 1] return ss - s_sqr / num dp_curr = [1e100] * (n + 1) dp_prev = [1e100] * (n + 1) dp_prev[0] = 0.0 for num_segments in range(1, k + 1): dp_curr[num_segments] = 0.0 for num_covered in range(num_segments + 1, n + 1): dp_curr[num_covered] = 1e100 for num_covered_previously in range(num_segments - 1, num_covered): dp_curr[num_covered] = min(dp_curr[num_covered], dp_prev[num_covered_previously] + get_best_sse(num_covered_previously + 1, num_covered)) dp_curr, dp_prev = dp_prev, dp_curr print(dp_prev[n])
C. Vorhersage von Nutzerklicks
Zustand
Eines der wichtigsten Signale für ein Empfehlungssystem ist das Benutzerverhalten. , .
..
2 : (train.csv) (test.csv). , . :
— sample_id — id ,
— item — id ,
— publisher — id ,
— user — id ,
topic_i, weight_i — id i- ( 0 100) (i = 0, 1, 2, 3, 4),
— target — (1 — , 0 — ). .
.
, item, publisher, user, topic .
csv-, : sample_id target, sample_id — id , target — . test.csv. sample_id ( , test.csv). target 0 1.
logloss.
150 . logloss :
logloss . 2 , logloss 4 .
/train.csv:
test.csv:
:
Hinweise
:
yadi.sk/d/pVna8ejcnQZK_A . , .
logloss :
EPS = 1e-4
def logloss(y_true, y_pred):
if abs (y_pred - 1) < EPS:
y_pred = 1 - EPS
if abs (y_pred) < EPS:
y_pred = EPS
return -y_true ∗ log(y_pred) - (1 - y_true) ∗ log(1 - y_pred)logloss logloss .
logloss :
def score(logloss):
if logloss > 0.5:
return 0.0
return min(150, (200 ∗ (0.5 - logloss)) ∗∗ 2) Lösung
, . . , (, , , ) , — , - , .
, 100 ( 150).
— CatBoost . CatBoost ( ), . , . , -:
( ), , , , - ( ).
. , - , : FM (Factorization Machines) FFM (Field-aware Factorization Machines).
,
ML- .