Faltungsschicht: schnelle Faltung nach der Methode von Shmuel Vinograd

Einleitung

Dieser Artikel ist eine Fortsetzung einer Reihe von Artikeln, in denen die zugrunde liegenden Algorithmen beschrieben werden.
Synet ist ein Framework zum Starten vorab trainierter neuronaler Netzwerke auf der CPU.

In einem früheren Artikel habe ich Methoden beschrieben, die auf Matrixmultiplikation basieren. Diese Methoden können mit minimalem Aufwand in vielen Fällen mehr als 80% des theoretischen Maximums erreichen. Wo können wir es wohl noch verbessern? Es stellt sich heraus, dass Sie können! Es gibt mathematische Methoden, mit denen die Anzahl der für die Faltung erforderlichen Operationen verringert werden kann. In diesem Artikel werden wir uns mit einer dieser Methoden vertraut machen, dem Faltungsalgorithmus nach der Vinograd-Methode.


Shmuel Winograd 1936.01.04 - 2019.03.25 - ein herausragender israelischer und amerikanischer Informatiker, der Algorithmen für schnelle Matrixmultiplikation, Faltung und Fourier-Transformation entwickelt hat.

Ein bisschen Mathe

Obwohl beim maschinellen Lernen am häufigsten Faltungen mit quadratischem Kern verwendet werden, wird zur Vereinfachung der Darstellung zunächst der eindimensionale Fall betrachtet. Angenommen, wir haben ein eindimensionales Eingabebild der Größe $$$1 \ times4$:

$$

$$d = \ begin {bmatrix} d_0 & d_1 & d_2 & d_3 \ end {bmatrix} ^ T,$$

und Filtergröße $$$1 \ times3$:

$$

$$g = \ begin {bmatrix} g_0 & g_1 & g_2 \ end {bmatrix} ^ T,$$

dann wird das Ergebnis der Faltung sein:

$$

$$F (2,3) = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix}.$$

Diese Ausdrücke werden bequem in Matrixform umgeschrieben:

$$

$$F (2,3) = \ begin {bmatrix} d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \ end {bmatrix} \ begin {bmatrix} g_0 \\ g_1 \\ g_2 \ end {bmatrix} = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix} = \ begin {bmatrix} m_1 + m_2 + m_3 \\ m_2 - m_3 - m_4 \ end {bmatrix}, (1)$$

wo die Notation verwendet wird:

$$

$$m_1 = (d_0-d_2) g_0, \\ m_2 = (d_1 + d_2) \ frac {g_0 + g_1 + g_2} {2}, \\ m_3 = (d_2-d_1) \ frac {g_0-g_1 + g_2} {2}, \\ m_4 = (d_1-d_3) g_2.$$

Auf den ersten Blick erscheint die letzte Ersetzung etwas sinnlos - es gibt deutlich mehr Operationen. Aber die Ausdrücke $$$\ frac {g_0 + g_1 + g_2} {2}$und $$$\ frac {g_0-g_1 + g_2} {2}$müssen nur einmal berechnet werden. Vor diesem Hintergrund müssen nur 4 Multiplikationsoperationen ausgeführt werden, während sie in der ursprünglichen Formel 6 ausgeführt werden müssen.
Wir schreiben Ausdruck (1) um:

$$

$$F (2,3) = A ^ T [(G g) \ odot (B ^ T d)], (2)$$

wo $$$\ odot$bezeichnet elementweise Multiplikation, und die folgende Notation wird auch verwendet:

$$

$$B ^ T = \ begin {bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1 \ end { bmatrix}, (3) \\ G = \ begin {bmatrix} 1 & 0 & 0 \\ \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {2} \\ \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {2} \\ 0 & 0 & 1 \ end {bmatrix}, (4) \\ A ^ T = \ begin {bmatrix} 1 & 1 & 1 & 0 \\ 0 & 1 & -1 & -1 \ end {bmatrix}. (5)$$

Der Ausdruck (2) kann auf den zweidimensionalen Fall verallgemeinert werden:

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A. (6)$$

Die erforderliche Anzahl von Multiplikationsoperationen für $$$F (2 \ times2,3 \ times3)$schrumpfen von $$$2 \ times2 \ times3 \ times3 = 36$vorher $$$4 \ times4 = 16$. So erhalten wir den Rechengewinn in $$$\ frac {36} {16} = $ 2,2$mal. Wenn Sie sich vorstellen, berechnen wir die Faltung für jeden Punkt im Bild, anstatt sie separat zu berechnen, sofort für einen Größenblock $$$2 \ times2$:

Auf jeden Fall zur Faltung mit dem Fenster $$$r \ times s$und Blockgröße $$$m \ times n$Die Anzahl der erforderlichen Multiplikationen beträgt

$$

$$count = (m + r - 1) \ times (n + s - 1), (7)$$

und der Gewinn wird durch die Formel beschrieben:

$$

$$k = \ frac {m \ mal n \ mal r \ mal s} {(m + r - 1) \ mal (n + s - 1)}. (8)$$

Im Limit für ausreichend groß $$$m$und $$$n$Für jede Faltung ist nur eine Multiplikation mit einem Punkt ausreichend! Leider führt eine Zunahme der Blockgröße zu einer schnellen Zunahme des Eingabe-Overheads $$$B ^ T d B$und wochenende $$$A ^ T [...] A$Bilder, also in der Praxis in der Regel keine Blockgröße größer als $$$4 \ times4$.

Implementierungsbeispiel

Für die praktische Implementierung des Vinograd-Algorithmus möchte ich den einfachsten Fall betrachten - die Faltung mit dem Kernel $$$3 \ times3$für den Block $$$2 \ times2$. Zur weiteren Vereinfachung der Darstellung wird außerdem davon ausgegangen, dass das Eingabebild nicht aufgefüllt wird und die Größe der Eingabe- und Ausgabebilder ein Vielfaches von 2 beträgt.

Die auf Matrixmultiplikation basierende Faltungsimplementierung sieht folgendermaßen aus:

float relu(float value) { return value > 0 ? return value : 0; } void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; for (int sc = 0; sc < srcC; ++sc) for (int ky = 0; ky < kernelY; ++ky) for (int kx = 0; kx < kernelX; ++kx) for (int dy = 0; dy < dstH; ++dy) for (int dx = 0; dx < dstW; ++dx) *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx]; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int M = dstC; int N = dstH * dstW; int K = srcC * kernelY * kernelX; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf); gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Wer genau wissen will, was hier vor sich geht, sollte sich meinem vorherigen Artikel zuwenden. Die aktuelle Implementierung ergibt sich aus der vorherigen, wenn wir sagen:

 strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0. 

Modifizierter Faltungsalgorithmus

Ich gebe hier noch einmal die Formel (6):

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A.$$

Wenn Sie von der Ausgabebildgröße wechseln $$$2 \ times2$zu einem Bild von beliebiger Größe, dann müssen wir es in Blöcke von Größe aufteilen $$$2 \ times2$. Für jeden solchen Block wird ein Eingabebild erzeugt $$$(2 + 3 - 1) \ times (2 + 3 - 1) = $ 1$Werte, die in 16 enthalten sind, konvertiert $$$B ^ T d B$Eingabebilder in halber Größe verkleinert. Dann wird jede dieser 16 Matrizen mit der entsprechenden Matrix der transformierten Gewichte multipliziert $$$G g G ^ T$. 16 resultierende Matrizen werden in das Ausgabebild konvertiert $$$A ^ T \ bigg [... \ bigg] A$. Darunter ist im Diagramm dieser Vorgang eingezeichnet:



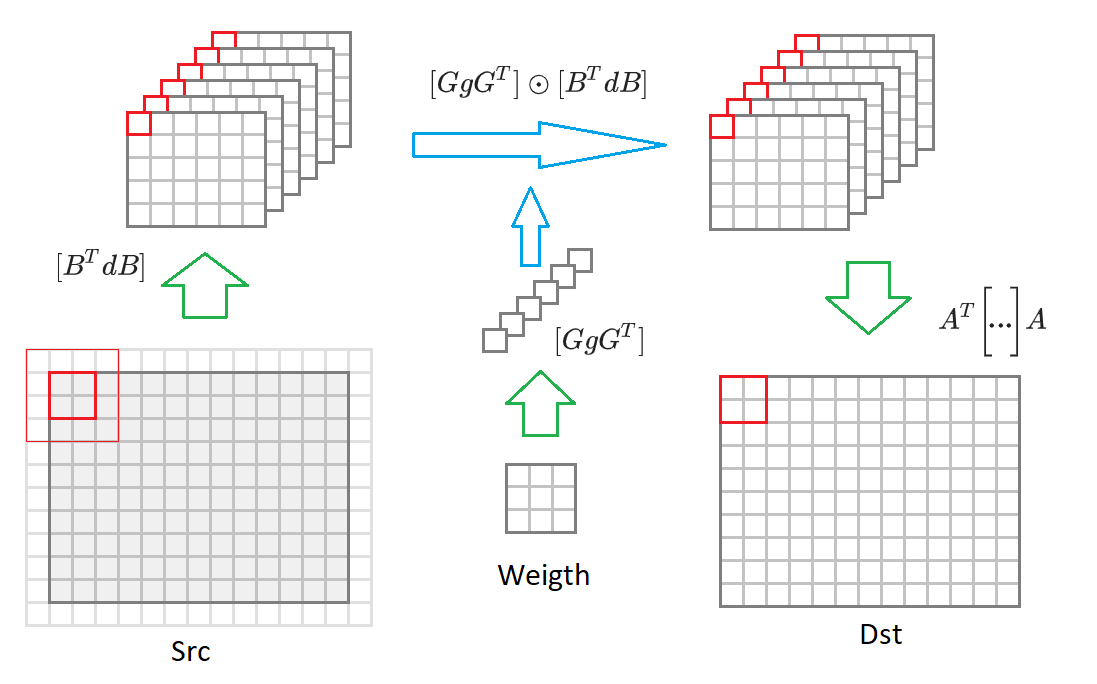
In Anbetracht dieser Kommentare hat der Faltungsalgorithmus die Form:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { const int block = 2, kernel = 3; int count = (block + kernel - 1)*(block + kernel - 1); // 16 int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int tileH = dstH / block; int tileW = dstW / block; int sizeW = srcC * dstC; int sizeS = srcC * tileH * tileW; int sizeD = dstC * tileH * tileW; int M = dstC; int N = tileH * tileW; int K = srcC; float * bufW = buf; float * bufS = bufW + sizeW*count; float * bufD = bufS + sizeS*count; set_filter(weight, sizeW, bufW); for (int b = 0; b < batch; ++b) { set_input(src, srcC, srcH, srcW, bufS, sizeS); for (int i = 0; i < count; ++i) gemm_nn(M, N, K, 1, bufW + i * sizeW, K, bufS + i * sizeS, N, 0, bufD + i * sizeD, N)); set_output(bufD, sizeD, dst, dstC, dstH, dstW); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Die Anzahl der Operationen, die erforderlich sind, ohne Transformationen des Eingabe- und Ausgabebilds zu berücksichtigen: ~ srcC * dstC * dstH * dstW * count . Als nächstes beschreiben wir die Algorithmen zum Konvertieren von Gewichten, Eingabe- und Ausgabebildern.

Konvertieren Sie Faltungsskalen

Wie aus Ausdruck (6) ersichtlich ist, sollte die folgende Transformation an Faltungsgewichten durchgeführt werden: $$$G g G ^ T$Wo ist die Matrix? $$$G$definiert in Ausdruck (4). Der Code für diese Konvertierung sieht folgendermaßen aus:

 void set_filter(const float * src, int size, float * dst) { for (int i = 0; i < size; i += 1, src += 9, dst += 1) { dst[0 * size] = src[0]; dst[1 * size] = (src[0] + src[2] + src[1])/2; dst[2 * size] = (src[0] + src[2] - src[1])/2; dst[3 * size] = src[2]; dst[4 * size] = (src[0] + src[6] + src[3])/2; dst[5 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4; dst[6 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4; dst[7 * size] = (src[2] + src[8] + src[5])/2; dst[8 * size] = (src[0] + src[6] - src[3])/2; dst[9 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4; dst[10 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4; dst[11 * size] = (src[2] + src[8] - src[5])/2; dst[12 * size] = src[6]; dst[13 * size] = (src[6] + src[8] + src[7])/2; dst[14 * size] = (src[6] + src[8] - src[7])/2; dst[15 * size] = src[8]; } } 

Glücklicherweise muss diese Konvertierung nur einmal durchgeführt werden. Daher wirkt es sich nicht auf die endgültige Leistung aus.

Eingabebildkonvertierung

Wie aus Ausdruck (6) ersichtlich, sollte die folgende Transformation für das Eingabebild durchgeführt werden: $$$B ^ T d B$Wo ist die Matrix? $$$B ^ T$definiert in Ausdruck (3). Der Code für diese Konvertierung sieht folgendermaßen aus:

 void set_input(const float * src, int srcC, int srcH, int srcW, float * dst, int size) { int dstH = srcH - 2; int dstW = srcW - 2; for (int c = 0; c < srcC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[16]; for (int r = 0; r < 4; ++r) for (int c = c; c < 4; ++c) tmp[r * 4 + c] = src[(row + r) * srcW + col + c]; dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]); dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]); dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]); dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]); dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]); dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]); dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]); dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]); dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]); dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]); dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]); dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]); dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]); dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]); dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]); dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]); dst++; } } src += srcW * srcH; } } 

Die Anzahl der für diese Konvertierung erforderlichen Operationen beträgt: ~ srcH * srcW * srcC * count .

Ausgabebildkonvertierung

Wie aus Ausdruck (6) ersichtlich, sollte die folgende Transformation für das Ausgabebild durchgeführt werden: $$$A ^ T [...] A$Wo ist die Matrix? $$$B ^ T$definiert in Ausdruck (5). Der Code für diese Konvertierung sieht folgendermaßen aus:

 void set_output(const float * src, int size, float * dst, int dstC, int dstH, int dstW) { for (int c = 0; c < dstC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[8]; tmp[0] = src[0 * size] + src[1 * size] + src[2 * size]; tmp[1] = src[1 * size] - src[2 * size] - src[3 * size]; tmp[2] = src[4 * size] + src[5 * size] + src[6 * size]; tmp[3] = src[5 * size] - src[6 * size] - src[7 * size]; tmp[4] = src[8 * size] + src[9 * size] + src[10 * size]; tmp[5] = src[9 * size] - src[10 * size] - src[11 * size]; tmp[6] = src[12 * size] + src[13 * size] + src[14 * size]; tmp[7] = src[13 * size] - src[14 * size] - src[15 * size]; dst[col + 0] = tmp[0] + tmp[2] + tmp[4]; dst[col + 1] = tmp[1] + tmp[3] + tmp[5]; dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6]; dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7]; src++; } dst += 2*dstW; } } } 

Die Anzahl der für diese Konvertierung erforderlichen Operationen beträgt: ~ dstH * dstW * dstC * count .

Merkmale der praktischen Umsetzung

Im obigen Beispiel haben wir den Vinohrad-Algorithmus für einen Größenblock beschrieben $$$2 \ times2$. In der Praxis wird am häufigsten eine fortgeschrittenere Version des Algorithmus verwendet: $$$F (4 \ times4,3 \ times3)$. In diesem Fall ist die Blockgröße $$$4 \ times4$und die Anzahl der transformierten Matrizen beträgt 36. Der Rechengewinn gemäß Formel (8) wird 4 erreichen. Das allgemeine Schema des Algorithmus ist das gleiche, nur die Matrix der Transformationsalgorithmen unterscheidet sich.

Auf Github gibt es ein kleines Projekt , mit dem Sie diese Matrizen mit Koeffizienten für eine beliebige Faltungskern- und Blockgröße berechnen können.

Wir haben eine Variante des Vinograd-Algorithmus für das NCHW - Bildformat vorgestellt , aber der Algorithmus kann für das NHWC- Format auf ähnliche Weise implementiert werden (ich habe im vorherigen Artikel ausführlicher über diese Bildformate gesprochen.

Trotz zusätzlicher Transformationen liegt die Hauptrechenlast im Vinograd-Algorithmus (mit seiner kompetenten Anwendung natürlich) immer noch in der Matrixmultiplikation. Glücklicherweise handelt es sich hierbei um eine Standardoperation, die in vielen Bibliotheken effektiv implementiert ist.

Transformationsfunktionen, die für verschiedene Plattformen für den Vinohrad-Algorithmus optimiert wurden, finden Sie hier .

Vor- und Nachteile des Traubenalgorithmus

Erstens natürlich die Profis:

• Der Algorithmus ermöglicht es, die Berechnung der Faltung mehrmals (meistens 2-3 Mal) zu beschleunigen. Somit ist es möglich, die Faltung schneller als die "theoretische" Grenze zu berechnen.
• Der Algorithmus stützt sich in seiner Implementierung auf den Standardmatrix-Multiplikationsalgorithmus.
• Es kann für verschiedene Eingabebildformate implementiert werden: NCHW , NHWC .
• Die Puffergröße zum Speichern von Zwischenwerten ist kleiner als die für den Matrixmultiplikationsalgorithmus erforderliche.

Na und wo ohne Minuspunkte:

• Der Algorithmus erfordert eine separate Implementierung der Konvertierungsfunktionen für jede Faltungskerngröße sowie für jede Blockgröße. Vielleicht ist dies einer der Hauptgründe dafür, dass es fast überall nur zur Faltung mit dem Kernel implementiert wird. $$$3 \ times3$.
• Mit zunehmender Blockgröße nimmt die Komplexität der Implementierung von Konvertierungsfunktionen rapide zu. Daher gibt es praktisch keine Implementierungen mit einer Blockgröße größer als $$$4 \ times4$.
• Der Algorithmus legt den Faltungsparametern strideY = strideY = dilationY = dilationX = group = 1 strenge Beschränkungen auf. Obwohl es theoretisch möglich ist, den Algorithmus zu implementieren, wenn diese Einschränkungen verletzt werden, ist er in der Praxis aufgrund der geringen Effizienz nur geringfügig anwendbar.
• Die Effizienz des Algorithmus nimmt ab, wenn die Anzahl der Eingabe- oder Ausgabekanäle im Bild gering ist (dies ist auf die Kosten für die Konvertierung der Eingabe- und Ausgabebilder zurückzuführen).
• Die Effizienz des Algorithmus nimmt für kleine Größen von Eingabebildern ab (die resultierenden Matrizen aus dem Eingabebild sind zu klein und der Standardmatrix-Multiplikationsalgorithmus wird für sie unwirksam).

Schlussfolgerungen

Die auf dem Vinograd-Algorithmus basierende Faltungsberechnungsmethode kann die Recheneffizienz im Vergleich zu der auf der einfachen Matrixmultiplikation basierenden Methode erheblich steigern. Leider ist es nicht universell und ziemlich schwer zu implementieren. Für eine Reihe von Sonderfällen gibt es schnellere Ansätze, deren Beschreibung ich auf die nächsten Artikel dieser Reihe verschieben möchte. Warten auf Feedback und Kommentare von Lesern. Ich hoffe du warst interessiert!

PS Dieser und andere Ansätze werden von mir im Convolution Framework als Teil der Simd- Bibliothek implementiert .
Dieses Framework basiert auf Synet , einem Framework zum Ausführen vorab trainierter neuronaler Netzwerke auf der CPU.