Gepostet von rakf
Im Rahmen des Summer of Hack 2019 bei Digital Security habe ich mich mit einem Stromangriff befasst und mit ChipWhisperer gearbeitet.
Was ist das?
Die Energieanalyse ist eine Art Angriff über Kanäle von Drittanbietern. Das heißt, Angriffe, die Informationen verwenden, die als Ergebnis der physischen Implementierung des Systems angezeigt werden.
Welche Informationen können für einen Angreifer nützlich sein:
- kryptografische Konvertierungszeit;
- Stromverbrauch;
- elektromagnetische Felder;
- Lärm etc.
Ein Energieangriff gilt als der universellste.
Warum funktioniert es?
Mikroprozessoren, Mikrocontroller, RAM und viele andere Logikschaltungen basieren auf CMOS-Technologie. Der Stromverbrauch von CMOS-Schaltungen besteht aus zwei Komponenten: statisch und dynamisch. Der statische Stromverbrauch ist sehr gering, was einer der Gründe für die Monopolisierung der Technologie ist. Die dynamische Leistung beruht auf dem Schalten von Transistoren und hängt von den verarbeiteten Daten und den durchgeführten Operationen ab. Da die statische Komponente hauptsächlich konstant ist, ist die Änderung der Gesamtleistung ausschließlich auf die dynamische Leistung zurückzuführen, und daher kann der Gesamtenergieverbrauch für die Analyse verwendet werden.
Toolkit
ChipWhisperer , ich habe die 2-teilige Version benutzt:

ChipWhisperer ist ein Open-Source-Toolkit zur Untersuchung der Sicherheit eingebetteter Geräte. Es ermöglicht Energieanalysen und fehlerbasierte Angriffe.
Die Gebühr beträgt 250 USD. Entwickler positionieren es als revolutionäre Lösung, da solche Komplexe nach Ansicht der Entwickler 30.000 US-Dollar kosten. Das Gerät besteht aus 2 Karten: Ziel- und Erfassungskarte.
Es gibt andere Versionen mit ihren Vorteilen (aber auch mit hohen Kosten). Sie können auch verschiedene Zielkarten, Erweiterungskarten und Sonden für eine vollständige Analyse Ihrer Geräte separat erwerben und ChipWhisperer nur zum Entfernen verwenden.
ChipWhisperer hat ein exzellentes Wiki , kleine Entwicklungslabors und ab der 5. Version sogar eine gute API- Dokumentation . Tracks werden mit ihrer Software vom angeschlossenen Gerät entfernt und als NumPy-Array aufgezeichnet.
Zuerst müssen Sie die Firmware für das Zielgerät schreiben. Im Rahmen des Labors werden die Chiffren AES, DES, TEA berücksichtigt. Für sie gibt es bereits fertige Firmware und Einstellungen zum Entfernen von Spuren (Anzahl der zu entnehmenden Proben, Offset, ADC-Frequenz usw.). Für unabhängige Forschungseinstellungen müssen experimentell ausgewählt werden.
Wie oben erwähnt, können Sie einen Fehler auf der Zielplatine auslösen: eine Fehlfunktion des Taktsignals verursachen, Anweisungen überspringen und geheime Informationen extrahieren.
In großen Komplexen wird ein Oszilloskop verwendet, um Spuren zu verfolgen.
Analyse
Es gibt verschiedene grundlegende Analysemethoden:
- einfache Leistungsanalyse (SPA);
- Differential Power Analysis (DPA);
- Leistungskorrelationsanalyse (CPA).
Eine einfache Leistungsanalyse umfasst eine visuelle Analyse des Leistungsgraphen. Zum Beispiel kann ein Passwort zeichenweise abgerufen werden, indem das Leistungsprofil bei Eingabe des richtigen Zeichens beobachtet und mit dem falschen verglichen wird.
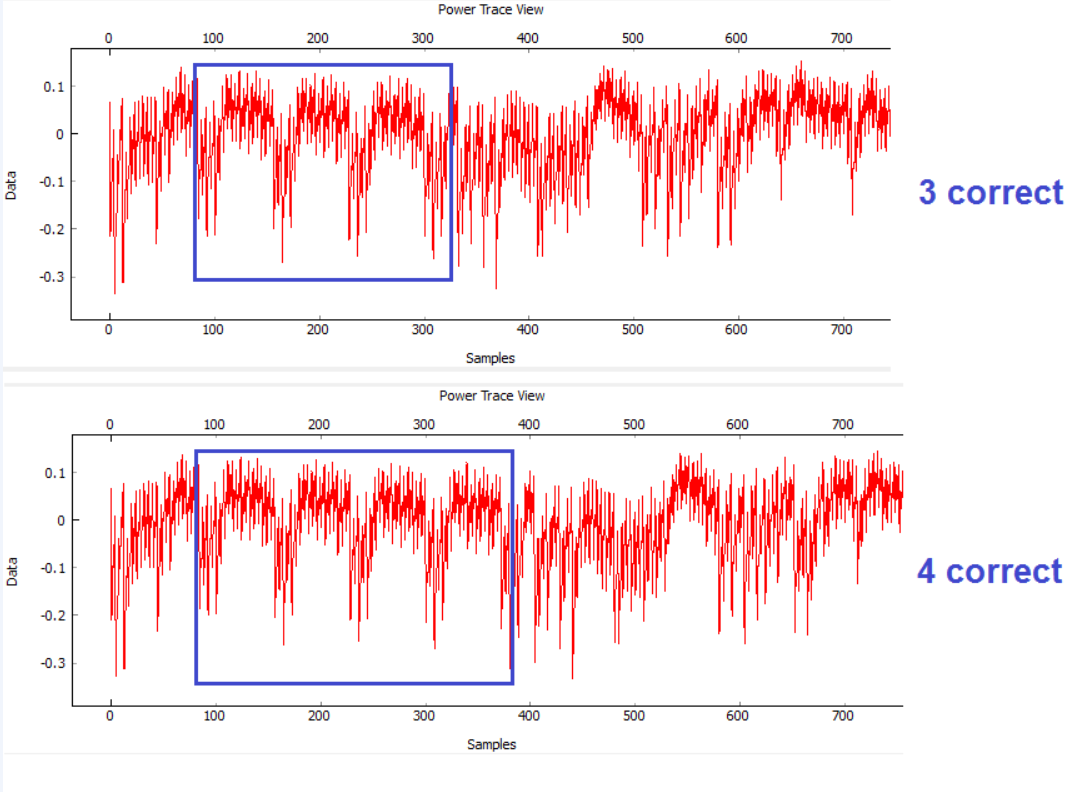
Oder Sie können die Verschlüsselungsrunden auf den Spuren sehen. Es sind nicht genügend Daten vorhanden, um einen Schlüssel zu erhalten, es kann jedoch davon ausgegangen werden, welcher Algorithmus ausgeführt wird. Die Abbildung zeigt deutlich 10 Runden AES.
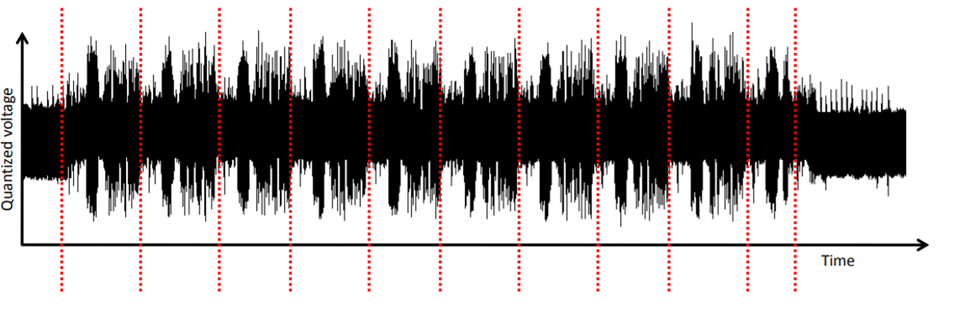
Die Differentialanalyse (DPA) ist viel effizienter als die einfache Analyse: Die DPA basiert auf statistischen Analysemethoden, um Unterschiede in den Leistungskurven zu erkennen. Ein sehr effektives Werkzeug zum „Öffnen“ des Schlüssels erfordert jedoch eine große Anzahl von Routen. Ich habe diese Methode nicht für die Analyse verwendet, aber am Ende werde ich einige Links zu Quellen angeben, in denen es gut beschrieben ist.
Grundlage der Korrelationsanalyse ist ein statistisches Gerät zur Ermittlung des geheimen Verschlüsselungsschlüssels. Manchmal wird es in einem separaten Typ isoliert, manchmal als DPA bezeichnet. Diese Methode erfordert weniger Spuren als DPA, ich habe sie für die Leistungsanalyse verwendet. Ich erzähle Ihnen mehr darüber.
Die Hauptaufgabe besteht darin, ein genaues Modell des Energieverbrauchs des untersuchten Geräts zu erstellen. Wenn ein genaues Modell erstellt wird, besteht eine merkliche Korrelation zwischen dem vorhergesagten und dem tatsächlichen Wert.
Eines der Power-Modelle, die verwendet werden können, ist das Hamming-Gewichtsmodell. Das Hamming-Gewicht ist die Anzahl der Nicht-Null-Werte in binärer Darstellung. Bei diesem Modell wird davon ausgegangen, dass die Anzahl der im Register gesetzten Bits mit der vom Gerät verbrauchten Energie korreliert. Hammings Gewicht selbst wird im Folgenden als herkömmliche Energieeinheit verwendet. Das Hamming-Distanzmodell wird ebenfalls verwendet - die Anzahl der verschiedenen Bits in 2 Werten.
Um das Hamming-Gewichtsmodell und den tatsächlichen Stromverbrauch zu vergleichen, wird ein linearer Pearson-Koeffizient verwendet. Es zeigt die lineare Abhängigkeit einer Größe von einer anderen. Bei einem korrekt konstruierten Modell beträgt dieser Koeffizient 1.
Der generalisierte CPA-Algorithmus besteht aus den folgenden Hauptschritten:
- Entfernen Sie den Stromverbrauch beim Konvertieren von Nachrichten auf einem unbekannten Schlüssel.
- Wir erstellen ein Modell des Energieverbrauchs des Chips, wenn für alle möglichen Varianten des Schlüssel-Unterblocks die gleichen Nachrichten konvertiert werden (256 Optionen für jedes Byte).
- Wir finden den linearen Korrelationskoeffizienten für den simulierten Stromverbrauch und real. Im Falle eines wahren Schlüssels wird der Koeffizient zu 1 tendieren;
- Der Algorithmus wird für die verbleibenden Schlüsselunterblöcke wiederholt.
Infolgedessen wird der Schlüssel in kleinen Teilen sequenziell wiederhergestellt. Wenn wir jeweils ein Byte des Schlüssels angreifen, verwenden wir 2 bis 8 Versuche für jeden Schlüssel. Wenn Sie beispielsweise AES - 128 auswählen, beträgt die Gesamtzahl der Versuche für 16 Byte des Schlüssels 2 12 , was viel besser ist, als 2 128 zu treffen.
Magma-Verschlüsselungsanalyse
Magma ist ein Code, der in GOST R 34.12.2015 definiert ist, tatsächlich derselbe GOST 28147-89, nur im Profil. Der verschlüsselte Block durchläuft 32 Runden, in denen einige Transformationen stattfinden. Der Schlüssel besteht aus 256 Bits, jeder Rundungsschlüssel ist Teil des Originals.
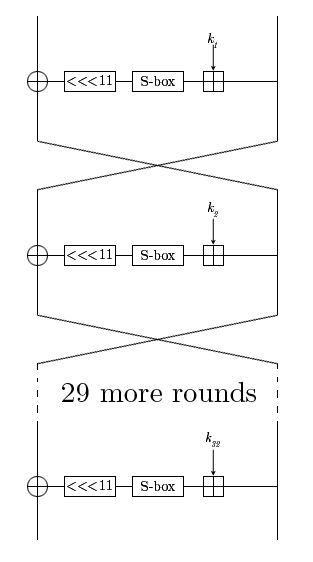
Wir werden die mit der CPA-Methode erhaltenen Daten analysieren.
Zunächst müssen Sie einen Zwischenwert für den Algorithmus auswählen, der von den bekannten Daten und einem kleinen Teil des Schlüssels abhängt und durch einfache Transformationen berechnet werden kann. Normalerweise ist dieser Wert die S-Box-Ausgabe (Magma hat jetzt 1 Substitutionstabelle, daher ist es einfacher, solche Angriffe auszuführen) der ersten (offene Texte sind bekannt) oder der letzten Runde (Geheimtexte sind bekannt).
Ich habe einen Schlüssel mit bekannten offenen Texten recherchiert, daher wird diese Option weiter geprüft. Im Gegensatz zu DES, AES erfolgt beim Magma-Algorithmus das Hinzufügen eines 32-Bit-Blocks mit einem runden Schlüssel modulo 2 32 , daher ist es besser, die Analyse an den letzten Ausgängen der S-Box zu starten, da das Hinzufügen der höchsten Werte die jüngeren nicht beeinflusst. Wir betrachten die Ausgabe jeder S-Box: zuerst 8, dann 8, 7 und so weiter bis zum ersten. Die Spurentfernung wurde auf einem 8-Bit-Mikrocontroller durchgeführt, und wir können davon ausgehen, dass dies mit zwei S-Boxen funktioniert hat. Daher werde ich sofort um 1 Byte angreifen.
Berechnung des Energiemodells für das letzte Schlüsselbyte:
for kguess in range(0, 256):
Wobei die Leak-Funktion einfach die S-Box-Ausgabe des letzten Bytes zurückgibt.
Wir berechnen den linearen Pearson-Koeffizienten für die simulierten und reellen Werte nach der Formel:
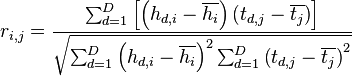
cpaoutput = [0]*256 maxcpa = [0]*256
Bei der Auswahl eines echten Unterschlüssels weist der Korrelationskoeffizient einen signifikanten Anstieg auf:
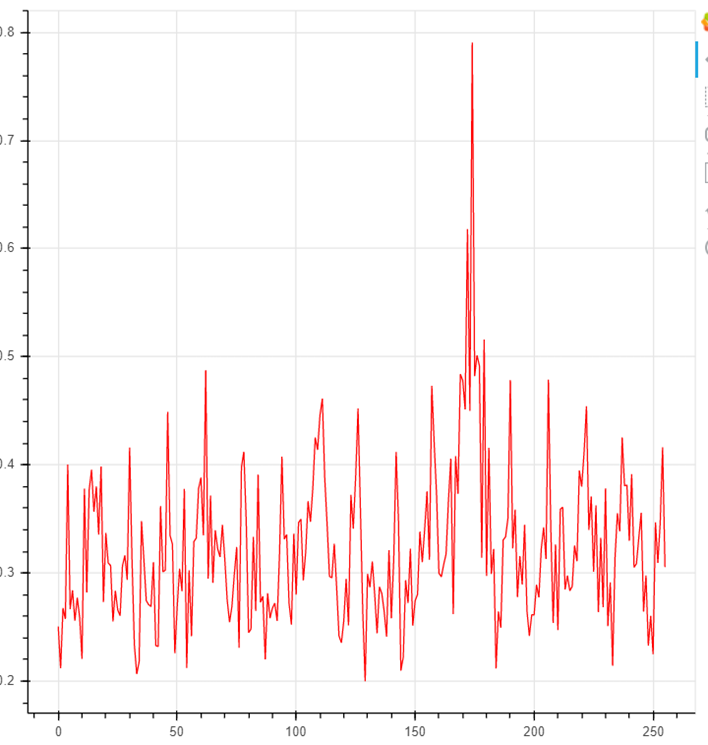
Somit wird jedes Byte des runden Schlüssels analysiert.
for bnum in range(0, 4): cpaoutput = [0]*256 maxcpa = [0]*256 for kguess in range(0, 256): best_round_key = kguess << (bnum * 8) | best_round ...
Mit dem ersten Rundenschlüssel können wir die 2 und die nachfolgenden Rundenschlüssel auf die gleiche Weise berechnen. Ein voller Magma-Schlüssel kann durch Herausnehmen von 8 runden Schlüsseln erhalten werden.
Bei der Lösung dieses Problems treten verschiedene Nuancen auf. Im Gegensatz zu AES, DES, Grasshopper-Chiffren erfolgt die Hinzufügung eines Klartext-Rundschlüssels modulo 2 32 . Das Hinzufügen von Low-Bits wirkt sich im Gegensatz zu XORa auf das High aus. Bei der Berechnung jedes nachfolgenden Unterschlüssels müssen Sie die Ergebnisse der Vergangenheit berücksichtigen. Ähnliches gilt für runde Schlüssel. Die Daten sind sehr sensibel. Wenn einer der Werte falsch berechnet wird, ist die weitere Berechnung des gesamten Schlüssels falsch.
Es ist auch zu bedenken, dass es heutzutage ziemlich schwierig ist, einen Chip mit einer Vier-Bit-Architektur zu finden: Die meisten Chips haben Acht-Bit-Architektur. Natürlich gibt es spezielle kryptografische Chips, die für einen bestimmten Sicherheitskonvertierungsalgorithmus (oder mehrere Algorithmen) entwickelt wurden und die effizienteste Architektur aufweisen.
Um die DES-Verschlüsselung auszuführen, kann ein solcher Kryptoprozessor für Magma eine Sechs-Bit-Architektur aufweisen - eine Vier-Bit-Architektur, mit der jede S-Box separat verarbeitet werden kann. Mein Zielgerät ist ein 8-Bit-Gerät, und im Fall von "Magma" wird die Konvertierung mit acht Bits in einem Ansatz durchgeführt, d. H. Der Austausch erfolgt an der 2 S-Box, der Stromverbrauch wird an der 2 S-Box berücksichtigt. Wenn eine der S-Boxen (Senior oder Junior) mit dem wahren Schlüssel übereinstimmt und die andere nicht übereinstimmt, können hohe Korrelationsbursts auftreten.
Aus all diesen Gründen haben wir am Ausgang das folgende Skript zur Analyse der Energieverbrauchspfade für die Magma-Chiffre:
Python-Skript import numpy as np path = r'C:\Users\user\chipwhisperer\projects\gost_10000_2_data\traces\2019.08.11-19.53.25_' traces = np.load(path + 'traces.npy') text = np.load(path + 'textin.npy') keys = np.load(path + 'keylist.npy') HW = [bin(n).count("1") for n in range(0,256)] SBOXES = {"Gost28147_tc26_ParamZ": ( (12, 4, 6, 2, 10, 5, 11, 9, 14, 8, 13, 7, 0, 3, 15, 1), (6, 8, 2, 3, 9, 10, 5, 12, 1, 14, 4, 7, 11, 13, 0, 15), (11, 3, 5, 8, 2, 15, 10, 13, 14, 1, 7, 4, 12, 9, 6, 0), (12, 8, 2, 1, 13, 4, 15, 6, 7, 0, 10, 5, 3, 14, 9, 11), (7, 15, 5, 10, 8, 1, 6, 13, 0, 9, 3, 14, 11, 4, 2, 12), (5, 13, 15, 6, 9, 2, 12, 10, 11, 7, 8, 1, 4, 3, 14, 0), (8, 14, 2, 5, 6, 9, 1, 12, 15, 4, 11, 0, 13, 10, 3, 7), (1, 7, 14, 13, 0, 5, 8, 3, 4, 15, 10, 6, 9, 12, 11, 2), )} def _K(s, _in): """ S-box substitution :param s: S-box :param _in: 32-bit word :returns: substituted 32-bit word """ return ( (s[0][(_in >> 0) & 0x0F] << 0) + (s[1][(_in >> 4) & 0x0F] << 4) + (s[2][(_in >> 8) & 0x0F] << 8) + (s[3][(_in >> 12) & 0x0F] << 12) + (s[4][(_in >> 16) & 0x0F] << 16) + (s[5][(_in >> 20) & 0x0F] << 20) + (s[6][(_in >> 24) & 0x0F] << 24) + (s[7][(_in >> 28) & 0x0F] << 28) ) def block2ns(data): """ Convert block to N1 and N2 integers """ data = bytearray(data) return ( data[7] | data[6] << 8 | data[5] << 16 | data[4] << 24, data[3] | data[2] << 8 | data[1] << 16 | data[0] << 24, ) def addmod(x, y, mod=2 ** 32): """ Modulo adding of two integers """ r = x + int(y) return r if r < mod else r - mod def _shift11(x): """ 11-bit cyclic shift """ return ((x << 11) & (2 ** 32 - 1)) | ((x >> (32 - 11)) & (2 ** 32 - 1)) def round(sbox, key, data, byte): s = SBOXES[sbox] _in = addmod(data, key) sbox_leak = _K(s, _in); return (sbox_leak >> (8 * byte)) & 0xFF def Feistel(sbox, key, data, nround): s = SBOXES[sbox] w = bytearray(key) x = [ w[3 + i * 4] | w[2 + i * 4] << 8 | w[1 + i * 4] << 16 | w[0 + i * 4] << 24 for i in range(8) ] n1, n2 = block2ns(data) for i in range(nround): n1, n2 = _shift11(_K(s, addmod(n1, x[i]))) ^ n2, n1 return n1 numtraces = len(traces) numpoint = np.shape(traces)[1] bestguess = [0]*32 round_data = [0] * numtraces for i in range(numtraces): round_data[i] = [0] * 8 for rnum in range(0, 8): best_round = 0 for tnum_r in range(numtraces): round_data[tnum_r][rnum] = Feistel("Gost28147_tc26_ParamZ", bestguess, text[tnum_r], rnum) for bnum in range(0, 4): cpaoutput = [0]*256 maxcpa = [0]*256 for kguess in range(0, 256):
GitHub Results Repository
Schlussfolgerungen
Im Rahmen der Studie habe ich mit ChipWhisperer gearbeitet. Trotz der Tatsache, dass ich nicht alle Tools ausprobiert habe (z. B. Glitching), finde ich ChipWhisperer auf jeden Fall nützlich, insbesondere, wenn Sie keine teure Spezialhardware kaufen möchten.
Die Analyse unserer Chiffre für den Stromverbrauch ist widerstandsfähiger gegen diesen Angriff als die oben beschriebenen Chiffren, aber mit genügend Daten kann der Schlüssel problemlos abgerufen werden.
Interessante Materialien: