Primzahlen - wie groß ist unsere Ohnmacht?

Stellen Sie sich vor, Sie sind von einer unendlich hohen Mauer umgeben, aber über das, was sich hinter der Mauer befindet, ist absolut nichts bekannt. Stellen Sie sich nun vor, dass die Personifikation dieser Mauer die folgende Gleichung ist:



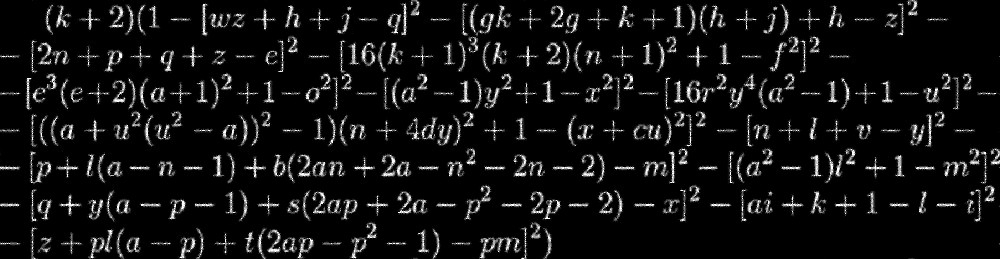
Diese Metapher wird leichter zu verstehen sein, wenn wir eine Analogie mit einem Schwarzen Loch ziehen: Wir wissen nicht, was sich unter seinem Ereignishorizont befindet, und um herauszufinden, müssen wir einen Weg finden, dorthin zu gelangen. Ähnliches gibt es in der Welt der Mathematik. Diese Gleichung ist eine echte "Formel" einer Primzahl, aber um sie zu verwenden, müssen wir herausfinden, wie wir nach geeigneten {a, b, c, d, e, f, g, i, j, k, l, m, n, o, p, q, w, v, x, y, z} .

Das Schwarze Loch und diese Gleichung sind die Endzustände von etwas Realem und Abstraktem. Und wenn es genug Vermutungen und Ideen über die erste gibt, dann ist über die zweite praktisch nichts bekannt. Aber was ist, wenn es wirklich ein "mathematisches" Schwarzes Loch ist? Sind Sie nicht neugierig, was passieren kann, wenn wir unter den Horizont fallen?

Woraus besteht die Mauer?

Zahlen - sie sind nicht in der realen Welt. Es gibt sieben Würfel, sieben Atome, sieben Todsünden, aber die sieben selbst existieren nicht - es ist eine Abstraktion. Ja, wir könnten sagen, dass Zahlen nur eine Menge abstrakter Objekte sind, dies ist jedoch eine ganze Welt. Eine Welt, in der es wie in der realen Welt Gesetze gibt. Der bloße Gedanke daran scheint sehr seltsam. Die Existenz eines solchen Zweigs der Mathematik als Zahlentheorie legt jedoch nahe, dass diese „Kuriosität“ für uns sehr wichtig ist.

Das Aufregendste ist, dass es unter diesen imaginären Objekten spezielle gibt - Primzahlen. Sie sind wie deterministisches Chaos - vorhersehbar und unvorhersehbar zugleich, je nach Umfang ihrer Überlegungen. Wenn wir uns zum Beispiel neben ihnen befinden, können wir feststellen, dass ihre Anzahl vor einer beliebigen Zahl n Folgendes nicht überschreitet:



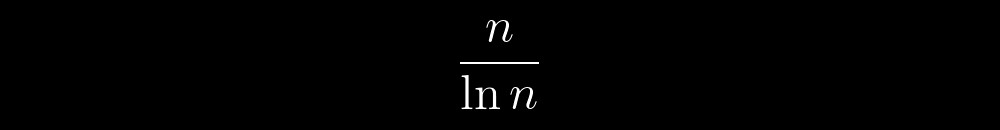
Wenn wir den Maßstab ändern, bemerken wir eine Menge Hinweise auf eine Art von internen Regeln für ihr Verhalten. Allmählich werden diese Hinweise zu viele. Immer häufiger die Fragen "Woher kommen sie?", "Was ist, wenn es einen bestimmten Algorithmus zum Erhalten von Primzahlen gibt?", "Was, wenn jede Primzahl mit demselben Algorithmus erhalten werden kann?"

Wie die Mauer aussah

Wenn eine bestimmte Folge von Zahlen als Ergebnis der Operation eines bestimmten Algorithmus erhalten wird, wird die Menge von Zahlen dieser Folge als aufzählbar betrachtet, obwohl sie unendlich groß sein kann. Aufzählungssätze haben eine bemerkenswerte Eigenschaft - Diophantine. Dies bedeutet, dass jede solche Menge durch eine diophantinische Gleichung dargestellt werden kann - ein Polynom mit ganzzahligen positiven Koeffizienten und Potenzen.

Die folgende Aussage mag völlig unplausibel erscheinen, aber basierend auf dieser Definition können wir argumentieren, dass alle Sicherheitsschlüssel und Werte von Hash-Funktionen (auch Bitcoins) durch diophantische Gleichungen ausgedrückt werden können. d.h. Gleichungen, die in ganzen Zahlen gelöst werden. Und ja, theoretisch kann jemand irgendwelche Geheimnisse lernen, unendlich reich und mächtig sein. Aber um eine solche Person zu werden, müssen diese Gleichungen zuerst abgeleitet und dann gelöst werden.

Der Computer kann die Aufgabe bewältigen, die Menge durch die diophantinische Gleichung teilweise oder vollständig darzustellen. Aber hier tritt ein anderes Problem auf - die diophantinischen Gleichungen werden nicht in einer allgemeinen Form gelöst, d.h. Es gibt keinen einzigen Algorithmus, um sie zu lösen. Dies scheint kein großes Problem zu sein, da wir wissen, dass einige Gleichungen in separate Formen unterteilt sind, für deren Lösung bereits wirksame Methoden gefunden wurden.

Aber trotz der Anwesenheit dieser Methoden treten unvermeidlich Rechenschwierigkeiten auf, die entweder mit der Genauigkeit der Berechnungen oder mit der Geschwindigkeit der Iterationen verbunden sind.

Wie kam es, dass Primzahlen aufzählbar waren? Der eigentliche Prozess der Erstellung von Gleichungen, die aufzählbare Mengen darstellen, beruht auf den Grundlagen der Mathematik - Arithmetik und Logik. Und wenn wir über genügend Wissen über die Eigenschaften von Objekten einer bestimmten Menge verfügen, können wir basierend auf diesem Wissen Annahmen über den Algorithmus treffen, mit dem sie erhalten werden können. Und wie sich herausstellte, wurde das Wissen über die Eigenschaften von Primzahlen für diesen Zweck ausreichend akkumuliert. Die Gleichung wurde erhalten, und jetzt werden alle Fragen, die sich auf Primzahlen beziehen, auf sie allein reduziert.

Aber wir können es nicht lösen.

Wandstärke und Festigkeit

Tatsächlich sind wir herausgefordert. Und wir wissen im Voraus über die unvermeidliche Niederlage. Vielleicht wäre ein Rückzug die klügste Entscheidung. Aber brauchen wir diese Niederlagen nicht, um uns selbst zu übertreffen? Lassen Sie uns versuchen, es nur ein bisschen zu lösen.

Schauen Sie sich die Gleichung noch einmal an:



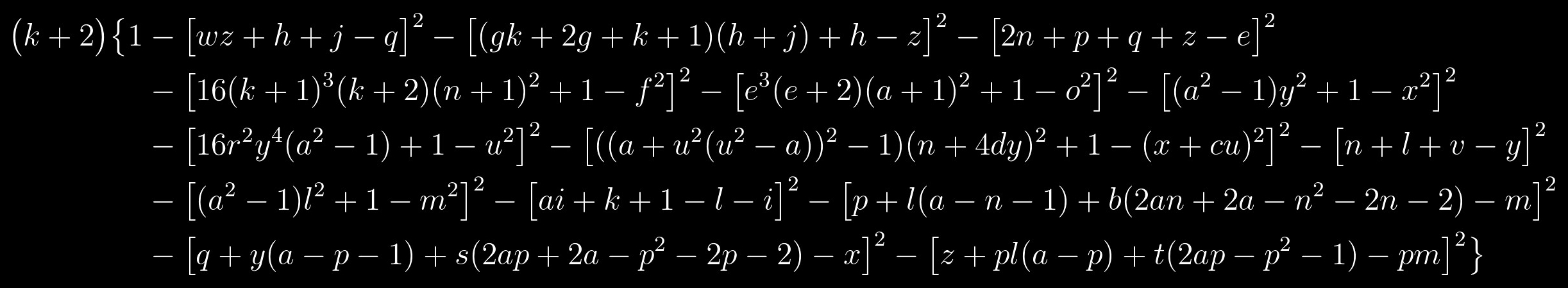
Dies ist ein Polynom, dessen Menge positiver Werte mit der Menge der Primzahlen übereinstimmt. Es besteht aus zwei Faktoren: Der linke Faktor ist nur dann eine Primzahl, wenn der rechte Faktor in geschweiften Klammern gleich eins ist, und dies ist wiederum nur möglich, wenn jeder Term im gegebenen Faktor in eckigen Klammern gleich null ist . Es stellt sich heraus, dass sich die Frage nach der Lösung dieser Gleichung auf die Lösung eines Systems der folgenden Gleichungen reduziert:



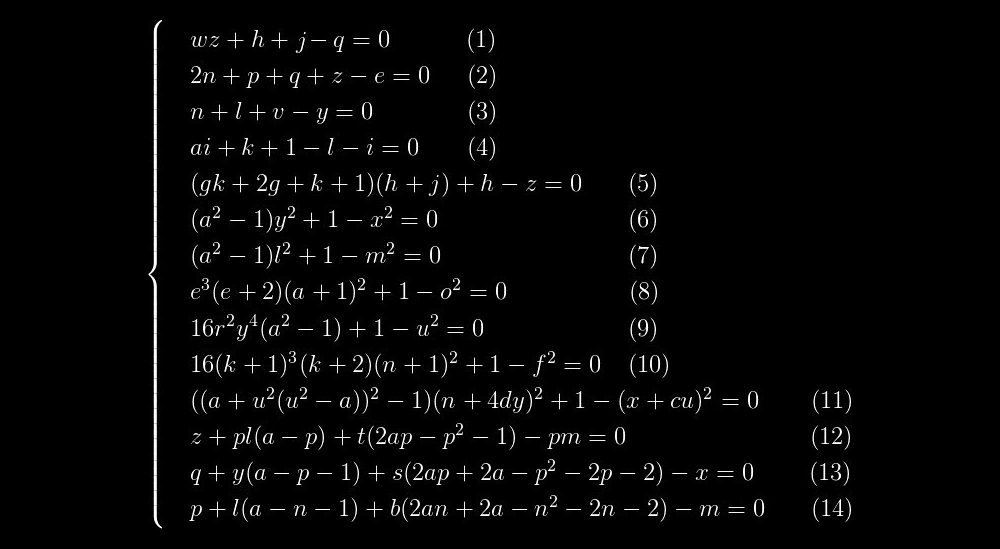
Wenn wir dieses Gleichungssystem lösen und 2 zum gefundenen Wert von k addieren, erhalten wir eine Primzahl. Aber wir können den anderen Weg gehen. Nehmen Sie eine Primzahl, subtrahieren Sie 2 davon, um den Wert von k zu erhalten , setzen Sie diesen Wert in das System ein und versuchen Sie, die Werte der verbleibenden Variablen relativ dazu zu finden. Auf diese Weise werden wir versuchen, mindestens eine Lösung für dieses Polynom zu finden.

Alle Variablen unterliegen zwei strengen Einschränkungen: Sie müssen ganzzahlig sein und dürfen nicht negativ sein. Wenn wir k = 0 nehmen , ist die erste Primzahl, die wir bekommen können, 2. Dies wird unser Ausgangspunkt sein. Nachdem dieser Wert in das Gleichungssystem eingesetzt wurde, hat er die folgende Form:



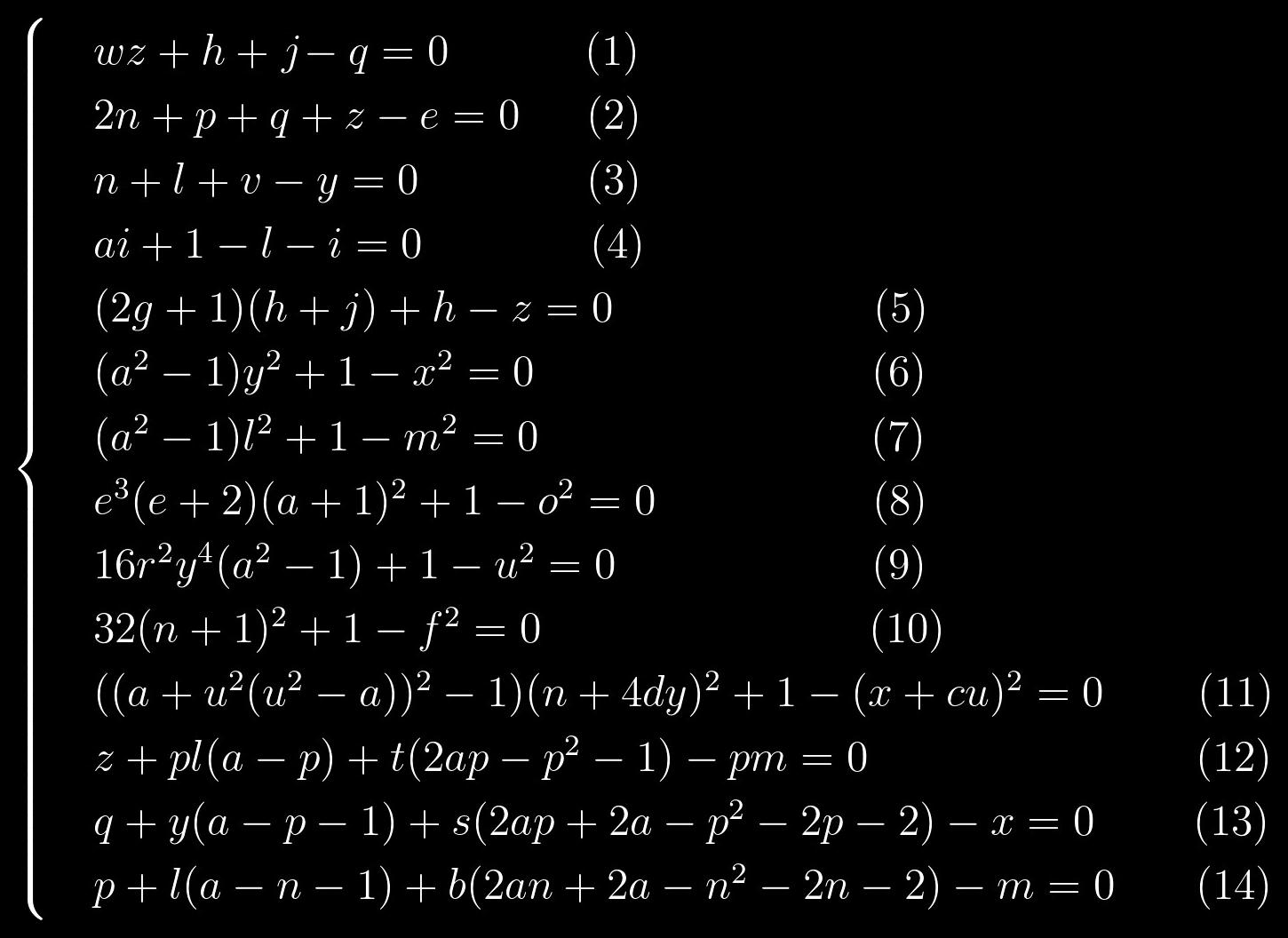
Die Gleichungen (1) - (5) sind lineare Gleichungen, d.h. Die Grade aller Variablen sind 1. Die Gleichungen (6) - (11) haben eine sehr ähnliche Struktur. Und schließlich stechen die Gleichungen (12) - (14) auch in einer separaten Gruppe heraus, und die Gleichungen (13) und (14) ähneln einander wie zwei Wassertropfen.

Wir können Variablen loswerden oder den Grad senken, aber das haben wir schon vorher gemacht. Eine Verringerung der Anzahl von Variablen führt zu einer starken Zunahme der Grade anderer Variablen, und eine Verringerung der Grade von Variablen ist nur durch eine Zunahme ihrer Anzahl möglich. Versuchen wir also, dieses System in dieser Form zu lösen.

Die Gleichungen (6) - (11) sind Modifikationen der Pell-Gleichung:



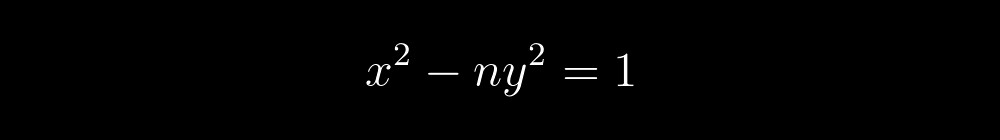
In der Tat, wenn Sie sie so umschreiben:



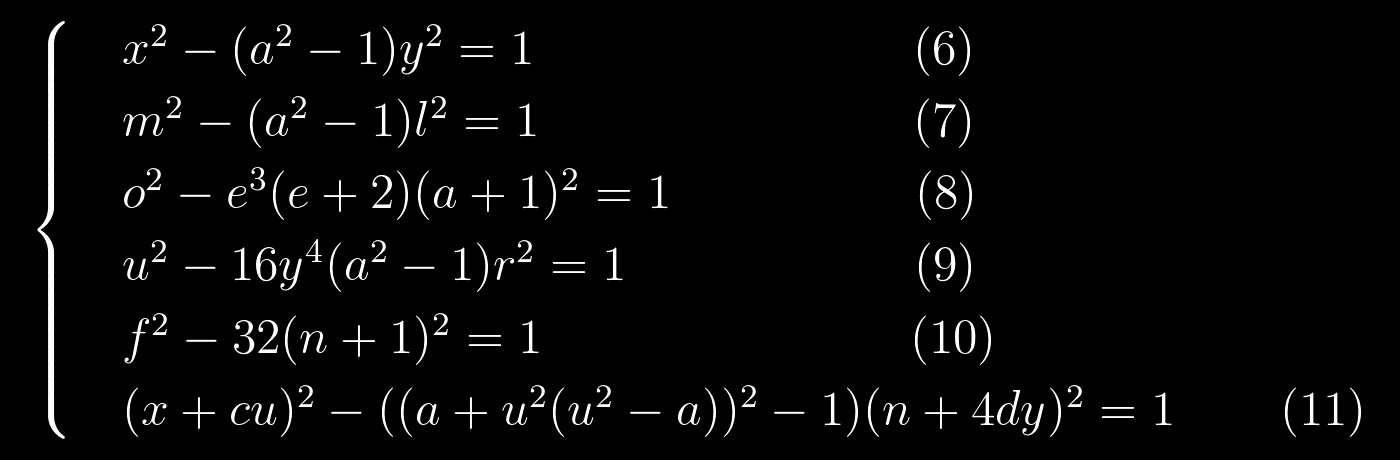
dann wird die Ähnlichkeit offensichtlich. Dies ist sehr ermutigend, da wir die Pell-Gleichungen recht gut lösen können. Wir können versuchen, dieses System so zu lösen: Zuerst lösen wir eine Gleichung, ersetzen ihre Lösungen durch eine andere, die wir auch lösen, und so weiter bis zum Ende. Es hört sich ziemlich einfach an, aber es würde nicht schaden, so etwas wie einen Permutationsgraphen zu zeichnen, um zumindest ungefähr zu wissen, in welcher Reihenfolge die Gleichungen zu lösen sind:


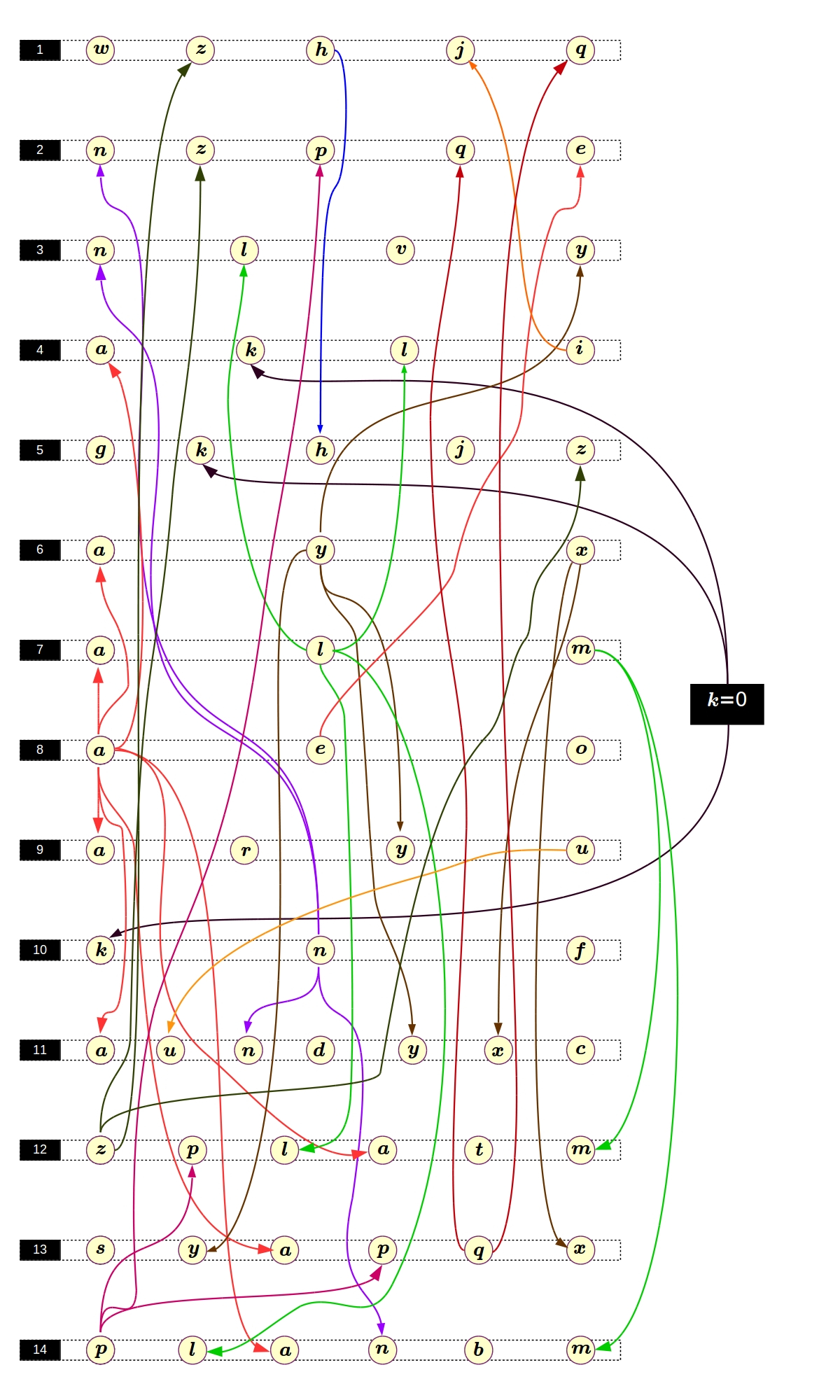
Es scheint, dass alles einfach ist.

Tritt gegen die Wand

Wir beginnen mit den Pell-Gleichungen. Um sie zu lösen, werden wir ein kleines Skript schreiben:

from decimal import * getcontext().prec = 50 def peq_dec(N): n = Decimal(N).sqrt() a = int(n) x = n - a p0, q0 = 1, 0 p1, q1 = int(a), 1 while True: a = int(1/x) x = 1/x - a p_i = a*p1 + p0 q_i = a*q1 + q0 if p_i**2 - N*q_i**2 == 1: return p_i, q_i break p0, q0 = p1, q1 p1, q1 = p_i, q_i 

Dank ihm finden wir sofort eine Lösung zu Gleichung (10) n = 2 , f = 17 . Bevor wir jedoch fortfahren, müssen wir etwas über die Pell-Gleichung wissen.



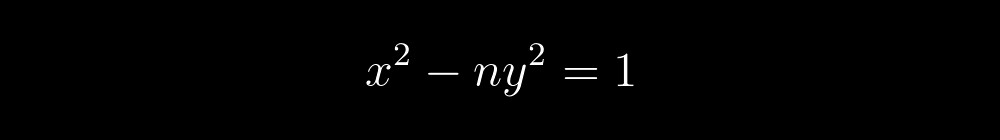
Zunächst kann n kein ganzes Quadrat sein. Darüber hinaus hat jede Pell-Gleichung eine unendliche Anzahl von Lösungen, von denen es immer eine triviale gibt: x = 1 und y = 0 . Jede nachfolgende Entscheidung kann auf der Grundlage der vorhergehenden Entscheidungen gemäß der folgenden Wiederholungsformel getroffen werden:



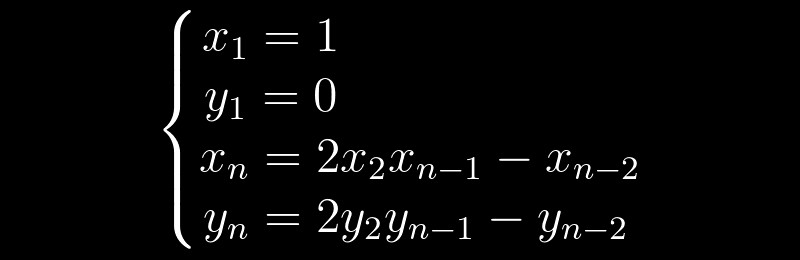
Es stellt sich heraus, dass es für uns ausreicht, die minimale, nicht triviale Lösung zu finden, und wir können den Rest mit einem einfachen Algorithmus erledigen. Zum Beispiel können wir für n = 2 leicht eine solche Lösung finden, es ist x = 3 und y = 2 , dann sehen nachfolgende Lösungen so aus:

 17, 12 99, 70 577, 408 3363, 2378 19601, 13860 114243, 80782 665857, 470832 3880899, 2744210 22619537, 15994428 131836323, 93222358 768398401, 543339720 4478554083, 3166815962 26102926097, 18457556052 152139002499, 107578520350 886731088897, 627013566048 

Lohnt es sich, die weitere Entscheidung fortzusetzen? Natürlich lohnt es sich, aber ... wir können versuchen, vorherzusagen, was vor uns liegt.

Stellen wir uns vorerst vor, wir lösen ein Gleichungssystem aus drei Pell-Gleichungen der folgenden Form:



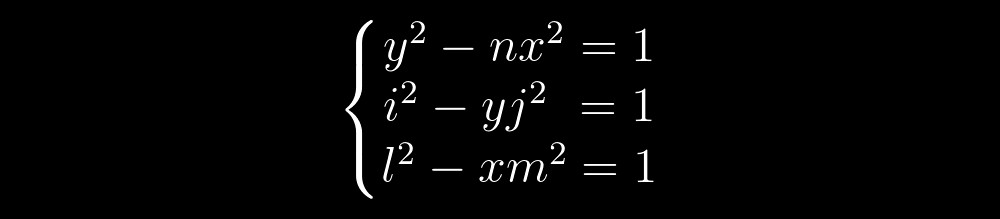
Die Lösung für jede Pell-Gleichung sind die Hyperbelpunkte mit ganzzahligen Koordinaten. Dann können wir uns eine Lösung für die ersten beiden Gleichungen vorstellen:



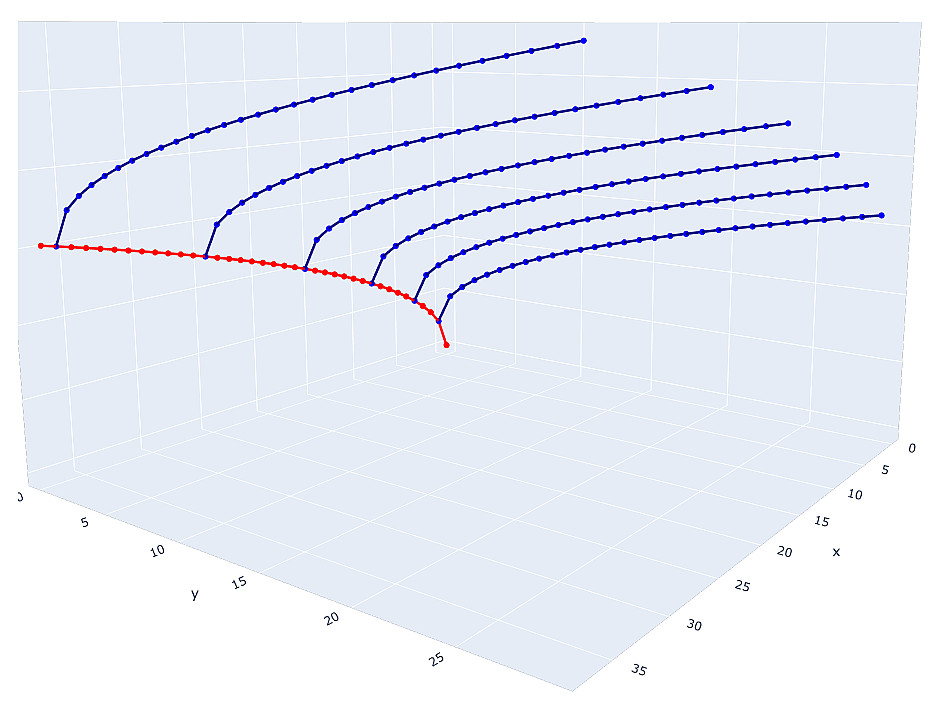
Die Lösung der ersten Gleichung sind die ganzzahligen Punkte der roten Hyperbel, aber die y- Koordinate jedes dieser Punkte ist in der zweiten Gleichung vorhanden und kann jede blaue Hyperbel erzeugen, deren ganzzahlige Punkte die Lösung der zweiten Gleichung sind.

Selbst diese schematische Darstellung reicht aus, um zu verstehen, dass es sich um eine sehr große Anzahl potenzieller Kandidaten für die Lösung des Systems handelt. Warum Kandidaten? Weil einige ganzzahlige Punkte der Hyperbel notwendigerweise volle Quadrate sein werden, d.h. unangemessene Lösungen. Und wenn Sie sich vorstellen, dass jeder Variablen im System zusätzliche Bedingungen auferlegt werden, wird es äußerst schwierig, Kandidaten für eine Lösung zu finden. Und wir sprechen bisher nur über ein System von drei Gleichungen.

Aber kehren wir zu unserer "Formel" der Primzahlen zurück. Was kann vor uns liegen?

Früher oder später werden wir feststellen, dass der Parameter n in der Pell-Gleichung katastrophal groß wird. Die Methode der fortgesetzten Brüche wird einfach unbrauchbar. Wir werden auf jeden Fall etwas anderes ausprobieren, zum Beispiel Werte mit Sieben aufzählen, den gesamten Prozess irgendwie verallgemeinern und zu Algorithmen wie einem quadratischen Sieb oder einem Sieb eines Zahlenfeldes kommen. Am Ende werden wir uns auf die "Chakraval" -Methode konzentrieren, obwohl sie auch einige Schwierigkeiten haben wird.

Zu einem bestimmten Zeitpunkt werden wir ein gewisses Vertrauen in die Lösung jeder einzelnen Gleichung des Systems haben. Aber nicht das ganze System. Wir werden versuchen, einige heuristische Optimierungsmethoden anzuwenden, beispielsweise einen Annealing-Algorithmus oder einen Ant-Algorithmus. Aber hier werden wir scheitern. Um die Gründe für diese Fehler zumindest irgendwie zu verstehen, müssen wir uns ein wenig mit algebraischer Geometrie und Topologie befassen. Allmählich werden wir eine Vorstellung von der „kristallisierbaren Substanz“ bekommen. Wir können uns die Struktur der Hyperfläche, auf der wir Ameisen freisetzen, aus der Ferne vorstellen.

Basierend auf diesen Ideen werden wir versuchen, unsere Algorithmen zu verbessern. Dazu werden wir die besten Leistungen aus vielen Bereichen der Mathematik ziehen. Allmählich haben die Algorithmen weniger Chancen, aber Sie können sie immer noch nicht entfernen. Was wird als nächstes passieren? Plötzlich stellen wir fest, dass viele geeignete Kandidaten für eine echte Entscheidung an einigen Orten paradoxerweise dicht sind. Jede solche Dichte gibt Hoffnung, dass irgendwo in ihrer Mitte die verborgene Antwort verborgen ist. Solche Dichten werden Ameisen wie ein umgekehrter Hypertunnel „vorkommen“. Wir werden versuchen, ihre Zentren und Höhen zu „treffen“. Aber was wird dann passieren?

Was ist hinter der Mauer?

Ich weiß wahrscheinlich nicht wie, aber wir werden diese Gleichung lösen. Vielleicht helfen uns Quanten- oder (!) Quark-Computer. Dies wird jedoch kein Loch in der Wand. Wahrscheinlich warten Gaußsche Primzahlen und eine noch kompliziertere Gleichung, die viele von ihnen darstellen wird, weiter auf uns. Dann werden wir vielleicht unter anderen hyperkomplexen Zahlen wieder auf eine Art "einfaches" Verhalten stoßen. Vielleicht ist dies am Ende die Grenze, eine Art Ereignishorizont für ein mathematisches Schwarzes Loch.

Was könnte sich unter diesem Horizont befinden? Wahrscheinlich eine Art mathematische Singularität. Wahrscheinlich werden wir absolut alles über alle Mengen wissen, wir werden in der Lage sein, alle Gleichungen und Probleme zu lösen. Oder gibt es vielleicht gar keine neuen Fragen und Aufgaben mehr?

Genau solche Gedanken entstehen. Stellen Sie tatsächlich eine Frage zu Primzahlen, und dank dieser Gleichung können Sie eine Antwort darauf erhalten. Ist die Anzahl der Doppelprimzahlen unendlich? Lösen Sie diese Gleichung, führen Sie einige algebraische Berechnungen durch und erhalten Sie die Antwort. Was sind die Primzahlen, die auf 1, 3, 7 oder 9 enden? Der gleiche Algorithmus: einige Berechnungen und Ersetzung der Gleichung. Möchten Sie Zahlen schnell in Primfaktoren zerlegen? ..

Abschließend

Ich habe diese Gleichung zum ersten Mal im Jahr 2008 kennengelernt und war schon verrückt nach Kryptographie und Zahlentheorie, insbesondere nach dem RSA-Schema und dem Faktorisierungsproblem. Natürlich erschien mir das Polynom, das Primzahlen erzeugt, als ein sehr interessantes Thema, aber zu kompliziert. Alle Probleme, die gelöst werden konnten oder nicht, waren jedoch irgendwie mit den diophantinischen Gleichungen verbunden. Deshalb habe ich mich bereits 2014 wieder diesem Polynom zugewandt und mich dazu entschlossen, einfach alle Abschnitte der Mathematik hintereinander zu untersuchen und nach etwas zu suchen, das zur Lösung hilfreich sein könnte. Natürlich kann von keiner akademischen Kultur all meiner Werke die Rede sein - ich habe nie systematische Aufzeichnungen geführt, nie den generierten Code aggregiert. Das ist nur mein Hobby.

Der Gedanke, diesen Artikel zu schreiben, kam auf, nachdem ich den Film Interstellar gesehen hatte. Ich konnte nicht glauben, dass Schwarze Löcher und Schwerkraft so verdammt aufregend dargestellt werden konnten. Aber wie sich herausstellte, versorgte mich die "nicht existierende" Welt der Mathematik die ganze Zeit mit den gleichen Eindrücken. Diese Welt hat auch ihren eigenen unzugänglichen "Deep Space" und ihre eigenen "Elementarteilchen".

Mit diesem Artikel wollte ich zeigen, dass es möglich ist, sich zumindest ein wenig jeder, schwierigsten, sogar unmöglichsten Aufgabe zu nähern. Es gibt viele solcher Aufgaben, und Sie können eine auswählen, die Ihren Wünschen entspricht und dem gewünschten Bereich am nächsten kommt. Natürlich wird übermäßige Komplexität und garantierte Niederlage den geringsten Wunsch in diesem Unternehmen berauben. Das ganze Paradox ist jedoch, dass die interessantesten Reisen und Abenteuer, selbst in der "nicht existierenden" Welt der Mathematik, meistens auf diese Weise beginnen.