Eine kürzlich durchgeführte Studie mit dem Titel
„Verwenden und Zuweisen von Stack-Overflow-Code-Snippets in GitHub-Projekten“ stellte plötzlich fest, dass meine
Antwort in Open Source-Projekten die meiste Zeit vor fast zehn Jahren verfasst wurde. Ironischerweise gibt es einen Fehler.
Es war einmal ...
2010 saß ich in meinem Büro und machte Unsinn: Ich hatte Spaß mit
Codegolf und gab Stack Overflow
eine Bewertung.
Die folgende Frage erregte meine Aufmerksamkeit: Wie kann ich die Anzahl der Bytes in einem lesbaren Format anzeigen? Das heißt, wie man so etwas wie 123456789 Bytes in "123,5 MB" konvertiert.
 Gute alte 2010-Schnittstelle, danke The Wayback Machine
Gute alte 2010-Schnittstelle, danke The Wayback MachineImplizit wäre das Ergebnis eine Zahl zwischen 1 und 999,9 mit der entsprechenden Einheit.
Es gab bereits eine Antwort mit einer Schleife. Die Idee ist einfach: Überprüfen Sie alle Grade von der größten Einheit (EB = 10
18 Bytes) bis zur kleinsten (B = 1 Byte) und wenden Sie die erste an, die kleiner als die Anzahl der Bytes ist. Im Pseudocode sieht es ungefähr so aus:
suffixes = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ] magnitudes = [ 10^18, 10^15, 10^12, 10^9, 10^6, 10^3, 10^0 ] i = 0 while (i < magnitudes.length && magnitudes[i] > byteCount) i++ printf("%.1f %s", byteCount / magnitudes[i], suffixes[i])
Normalerweise ist es schwierig, mit der richtigen Antwort mit einer positiven Bewertung mitzuhalten. In der Fachsprache Stack Overflow wird dies als das
Problem des schnellsten Schützen im Westen bezeichnet . Aber hier hatte die Antwort einige Fehler, also hoffte ich immer noch, sie zu übertreffen. Zumindest Code mit einer Schleife kann stark reduziert werden.
Nun, das ist Algebra, alles ist einfach!
Dann dämmerte es mir. Die Präfixe sind Kilo-, Mega-, Giga-, ... - nicht mehr als Grad 1000 (oder 1024 in der IEC-Norm), sodass das richtige Präfix anhand des Logarithmus und nicht anhand des Zyklus bestimmt werden kann.
Ausgehend von dieser Idee habe ich Folgendes veröffentlicht:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
Natürlich ist dies nicht sehr gut lesbar und log / pow ist in der Effizienz anderen Optionen unterlegen. Aber es gibt keine Schleife und fast keine Verzweigung, daher ist das Ergebnis meiner Meinung nach ziemlich schön.
Mathematik ist einfach . Die Anzahl der Bytes wird ausgedrückt als byteCount = 1000 s , wobei s den Grad darstellt (in binärer Notation beträgt die Basis 1024). Die Lösung s ergibt s = log 1000 (byteCount).
Es gibt keinen einfachen Ausdruck log 1000 in der API, aber wir können ihn in Form des natürlichen Logarithmus wie folgt ausdrücken: s = log (byteCount) / log (1000). Dann konvertieren wir s in int. Wenn wir zum Beispiel mehr als ein Megabyte (aber kein volles Gigabyte) haben, wird MB als Maßeinheit verwendet.
Es stellt sich heraus, dass wenn s = 1, dann ist die Dimension Kilobyte, wenn s = 2 - Megabyte und so weiter. Teilen Sie byteCount durch 1000 s und setzen Sie den entsprechenden Buchstaben in das Präfix.
Es blieb nur abzuwarten, wie die Community die Antwort wahrnahm. Ich konnte mir nicht vorstellen, dass dieser Code der am weitesten verbreitete in der Geschichte von Stack Overflow wird.
Attribution Study
Schneller Vorlauf bis 2018. Der Doktorand Sebastian Baltes veröffentlicht einen Artikel in der Fachzeitschrift
Empirical Software Engineering mit dem Titel
„Verwenden und Zuweisen von Code-Snippets für den Stapelüberlauf in GitHub-Projekten“ . Das Thema seiner Forschung ist, wie sehr die Stack Overflow CC BY-SA 3.0-Lizenz respektiert wird, das heißt, verweisen Autoren auf Stack Overflow als Quellcode?
Zur Analyse wurden Codeausschnitte aus dem
Stack Overflow-Dump extrahiert und dem Code in den öffentlichen GitHub-Repositorys zugeordnet. Zitat aus dem Abstract:
Wir präsentieren die Ergebnisse einer groß angelegten empirischen Studie, die die Verwendung und Zuordnung von nicht-trivialen Fragmenten von Java-Code aus SO-Antworten in öffentlichen GitHub (GH) -Projekten analysiert.
(Spoiler: Nein, die meisten Programmierer erfüllen die Lizenzanforderungen nicht.)
Der Artikel hat eine solche Tabelle:
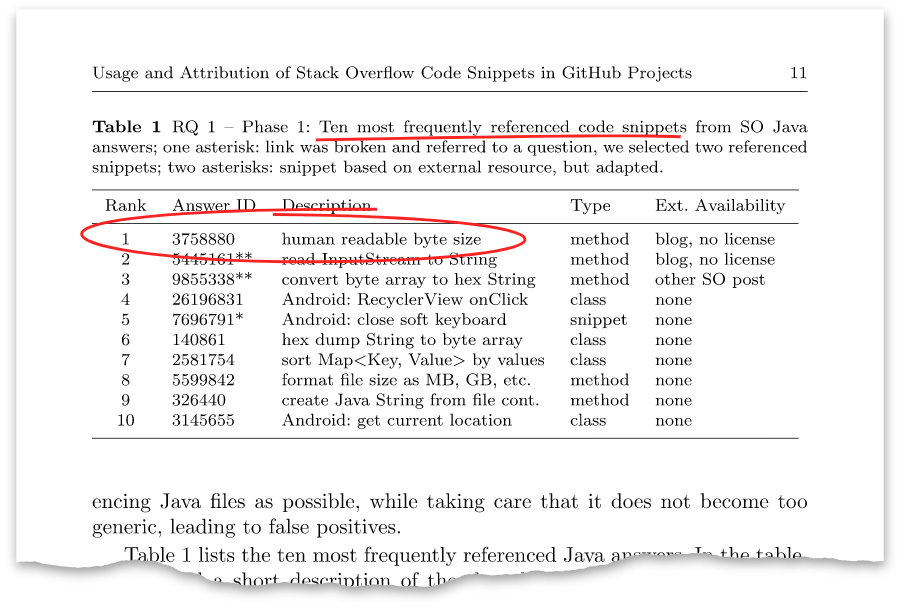
Diese Antwort oben mit der Kennung
3758880 hat sich als die Antwort herausgestellt, die ich vor acht Jahren gepostet habe. Im Moment hat er mehr als hunderttausend Aufrufe und mehr als tausend Pluspunkte.
Eine schnelle Suche in GitHub erzeugt wirklich Tausende von Repositories mit dem Code
humanReadableByteCount .
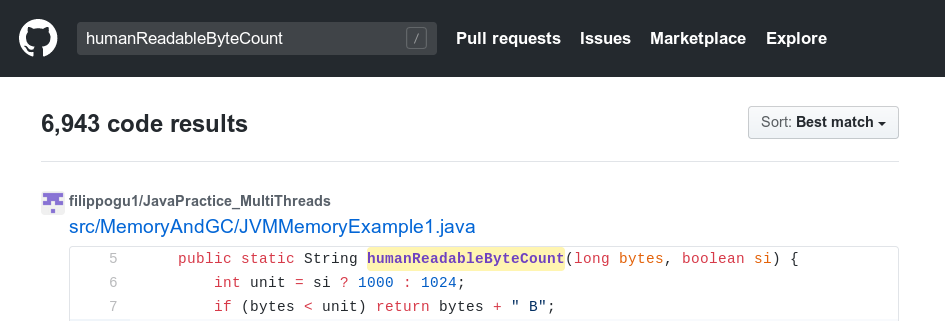
Suchen Sie nach diesem Fragment in Ihrem Repository:
$ git grep humanReadableByteCount
Eine lustige Geschichte , wie ich über diese Studie erfahren habe.
Sebastian hat im OpenJDK-Repository eine Übereinstimmung ohne Zuordnung gefunden, und die OpenJDK-Lizenz ist nicht mit CC BY-SA 3.0 kompatibel. Auf der Mailingliste von jdk9-dev fragte er: Wird der Stack Overflow-Code von OpenJDK kopiert oder umgekehrt?
Das Lustige ist, dass ich gerade in Oracle im OpenJDK-Projekt gearbeitet habe, also hat mein ehemaliger Kollege und Freund Folgendes geschrieben:
Hallo,
Warum fragst du den Autor dieses Beitrags nicht direkt bei SO (aioobe)? Er ist Mitglied von OpenJDK und arbeitete bei Oracle, als dieser Code in den OpenJDK-Quellrepositorys erschien.
Oracle nimmt diese Probleme sehr ernst. Ich weiß, dass einige Manager erleichtert waren, als sie diese Antwort lasen und den „Schuldigen“ fanden.
Dann schrieb Sebastian mir, um die Situation zu klären, die ich tat: Dieser Code wurde hinzugefügt, bevor ich zu Oracle kam, und ich habe nichts mit dem Festschreiben zu tun. Es ist besser, nicht mit Oracle zu scherzen. Einige Tage nach dem Öffnen des Tickets wurde dieser Code gelöscht .
Bug
Ich wette, du hast schon darüber nachgedacht. Welche Art von Fehler im Code?
Noch einmal:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
Welche Möglichkeiten gibt es?
Nach Exabytes (10
18 ) folgen Zettabytes (10
21 ). Vielleicht geht eine wirklich große Anzahl über kMGTPE hinaus? Nein. Der Maximalwert ist 2
63 -1 ≈ 9,2 × 10
18 , sodass kein Wert über Exabyte hinausgeht.
Vielleicht die Verwechslung zwischen SI-Einheiten und dem Binärsystem? Nein. Es gab Verwirrung in der ersten Version der Antwort, aber es wurde ziemlich schnell behoben.
Vielleicht endet exp mit dem Nullabgleich, wodurch charAt (exp-1) abstürzt? Auch nicht. Die erste if-Anweisung behandelt diesen Fall. Der Exp-Wert wird immer mindestens 1 sein.
Vielleicht ein seltsamer Rundungsfehler in der Auslieferung? Na endlich ...
Viele Neuner
Die Lösung funktioniert, bis sie sich 1 MB nähert. Wenn
"1000,0 kB" Bytes als Eingabe angegeben werden, ist das Ergebnis (im SI-Modus)
"1000,0 kB" . Obwohl 999.999 näher an 1000 × 1000
1 liegt als an 999,9 × 1000
1 , ist der Signifikator 1000 durch die Spezifikation verboten. Das korrekte Ergebnis ist
"1.0 MB" .
Zu meiner Verteidigung kann ich sagen, dass zum Zeitpunkt des Schreibens ein solcher Fehler in allen 22 veröffentlichten Antworten vorlag, einschließlich Apache Commons und Android-Bibliotheken.
Wie kann ich das beheben? Zunächst ist zu beachten, dass sich der Exponent (exp) von 'k' nach 'M' ändern muss, sobald die Anzahl der Bytes näher an 1 × 1.000
2 (1 MB) liegt als an 999,9 × 1000
1 (999,9 k) ) Dies geschieht bei 999.950. Ebenso sollten wir von 'M' zu 'G' wechseln, wenn wir 999.950.000 und so weiter durchlaufen.
Wir berechnen diesen Schwellenwert und erhöhen
exp wenn
bytes größer sind:
if (bytes >= Math.pow(unit, exp) * (unit - 0.05)) exp++;
Mit dieser Änderung funktioniert der Code gut, bis sich die Anzahl der Bytes 1 EB nähert.
Mehr Neunen
Bei der Berechnung von 999 949 999 999 999 999 999 ergibt der Code
1000.0 PB , und das korrekte Ergebnis ist
999.9 PB . Mathematisch gesehen ist der Code korrekt. Was passiert also hier?
Jetzt stehen wir vor
double Einschränkungen.
Einführung in die Gleitkomma-Arithmetik
Gemäß der IEEE 754-Spezifikation haben Gleitkommawerte nahe Null eine sehr dichte Darstellung, während große Werte eine sehr spärliche Darstellung haben. Tatsächlich liegt die Hälfte aller Werte zwischen -1 und 1, und bei großen Zahlen bedeutet ein Wert der Größe Long.MAX_VALUE nichts. Im wahrsten Sinne des Wortes.
double l1 = Double.MAX_VALUE; double l2 = l1 - Long.MAX_VALUE; System.err.println(l1 == l2); // prints true
Siehe "Gleitkomma-Bits" für Details.
Das Problem wird durch zwei Berechnungen dargestellt:
String.format in String.format und
- Expansionsschwelle
exp
Wir können auf
BigDecimal , aber es ist langweilig. Darüber hinaus treten auch hier Probleme auf, da die Standard-API keinen Logarithmus für
BigDecimal .
Zwischenwerte reduzieren
Um das erste Problem zu lösen, können wir den Wert von
bytes auf den gewünschten Bereich reduzieren, in dem die Genauigkeit besser ist, und
exp entsprechend anpassen. In jedem Fall ist das Endergebnis gerundet, so dass es keine Rolle spielt, dass wir die am wenigsten signifikanten Ziffern wegwerfen.
if (exp > 4) { bytes /= unit; exp--; }
Einstellung der niedrigstwertigen Bits
Um das zweite Problem zu lösen
, sind uns
die niedrigstwertigen Bits
wichtig (99994999 ... 9 und 99995000 ... 0 müssen unterschiedliche Grade haben), daher müssen wir eine andere Lösung finden.
Beachten Sie zunächst, dass es 12 verschiedene Schwellenwerte gibt (6 für jeden Modus), von denen nur einer zu einem Fehler führt. Ein falsches Ergebnis kann eindeutig identifiziert werden, da es mit D00
16 endet. So können Sie es direkt beheben.
long th = (long) (Math.pow(unit, exp) * (unit - 0.05)); if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 52 : 0)) exp++;
Da wir bei Fließkommaergebnissen auf bestimmte Bitmuster angewiesen sind, verwenden wir den Modifikator strictfp, um sicherzustellen, dass der Code unabhängig von der Hardware funktioniert.
Negative Eingabewerte
Es ist nicht klar, unter welchen Umständen eine negative Anzahl von Bytes sinnvoll sein kann, aber da Java keine vorzeichenlose
long , ist es am besten, mit dieser Option umzugehen. Im
-10000 B ergibt
-10000 B Eingabe von
-10000 BSchreiben
absBytes :
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
Der Ausdruck ist so ausführlich, weil
-Long.MIN_VALUE == Long.MIN_VALUE . Jetzt führen wir alle
exp Berechnungen mit
absBytes anstelle von
bytes .
Endgültige Fassung
Hier ist die endgültige Version des Codes, gekürzt und verkürzt im Geiste der Originalversion:
Beachten Sie, dass dies als Versuch begann, Schleifen und übermäßige Verzweigungen zu vermeiden. Nachdem alle Randbedingungen geglättet wurden, war der Code noch schlechter lesbar als die Originalversion. Persönlich würde ich dieses Fragment nicht in der Produktion kopieren.
Eine aktualisierte Version der Produktionsqualität finden Sie in einem separaten Artikel:
„Formatieren der Bytegröße in einem lesbaren Format“.Schlüsselergebnisse
- Die Antworten auf Stack Overflow enthalten möglicherweise Fehler, auch wenn sie Tausende von Pluspunkten aufweisen.
- Überprüfen Sie alle Grenzfälle, insbesondere im Code mit Stapelüberlauf.
- Fließkomma-Arithmetik ist kompliziert.
- Stellen Sie sicher, dass Sie beim Kopieren des Codes die richtige Zuordnung angeben. Jemand kann Sie zu sauberem Wasser bringen.