Einleitung
Der Artikel beschreibt die "Y-Methode" zum Zusammensetzen des Zauberwürfels - sie ist leicht zu verstehen und zu merken. Es basiert auf nur einer Sequenz, die als "Y-Bewegung" bezeichnet wird. Wenn Sie diesen Algorithmus verstanden haben, werden Sie wahrscheinlich nicht vergessen, wie Sie den Würfel selbst zusammenbauen.
Wenn Sie versuchen, die Montageanleitungen für den Rubik's Cube zu googeln, gibt es viele Optionen mit einer Beschreibung der "einfachen Montage", einschließlich auf
Wikipedia . Die im Allgemeinen recht einfach zu verstehen sind, aber einen erheblichen Nachteil haben. Um einen Würfel zusammenzusetzen, müssen Sie über fünf oder mehr nicht-triviale Sequenzen (Algorithmen) verfügen, um einzelne Würfel neu anzuordnen und einen Zauberwürfel in Ebenen zusammenzusetzen. In diesem Zusammenhang ist es schwierig, sich diese Anweisungen unabhängig voneinander zu merken und wiederzugeben. Kürzlich bin ich versehentlich auf die Erwähnung des Algorithmus „
Die ultimative Lösung für Rubiks Würfel “ gestoßen, der einfach zu merken und zu verstehen ist und nur zwei Sequenzen verwendet. Und als ich anfing, es genauer herauszufinden, fand ich auch einen anderen Algorithmus - die „
Y-Methode “, die ebenfalls einfach ist und nur eine Sequenz verwendet.
Leider habe ich keine Beschreibung dieses Algorithmus auf Russisch gefunden, also habe ich beschlossen, diese Lücke zu füllen. Mir scheint auch, dass die Hauptsache bei dieser Methode darin besteht, zu verstehen, wie sie funktioniert. Deshalb biete ich hier keine vorgefertigten Bewegungssätze für bestimmte Situationen an, sondern habe versucht, genauer zu beschreiben, was passiert.
Die Bilder in diesem Artikel wurden mit dem Tool auf
ruwix.com erstellt . Links zu Bildern öffnen dieses Tool mit Parametern, die dem Bild entsprechen. Dies ist entweder der beschriebene Zustand des Würfels und Sie können ihn mit der Maus drehen, oder in einigen Fällen werden dort die beschriebenen Bewegungen angegeben, die "verloren" gehen können.
Y Bewegung
Die Basis dieses Algorithmus ist die Y-Bewegung. Und eine ziemlich wichtige Komponente des Algorithmus ist es, die Mechanik dieser Bewegung zu verstehen.
Diese Abfolge von Drehungen wird so genannt, weil die Würfel, die sie berühren, wie der Buchstabe „Y“ aussehen, der aus drei Kanten besteht, die aus einer Ecke des Würfels herausragen.

Die Y-Bewegung ist recht einfach und besteht aus vier Windungen zweier benachbarter Flächen, beispielsweise der rechten und der vorderen. In einer üblichen Rotationsnotation für einen Rubik's Cube sieht es so aus: R 'FR F'. Was kann wie folgt beschrieben werden:
- rechte Seite eine Vierteldrehung gegen den Uhrzeigersinn
- Vorderseite im Uhrzeigersinn eine viertel Umdrehung
- rechte Seite viertel im Uhrzeigersinn drehen
- Vorderseite eine Vierteldrehung gegen den Uhrzeigersinn
Das heißt, die Gesichter werden zuerst "zu sich selbst" und dann in umgekehrter Reihenfolge "von sich selbst" gedreht.
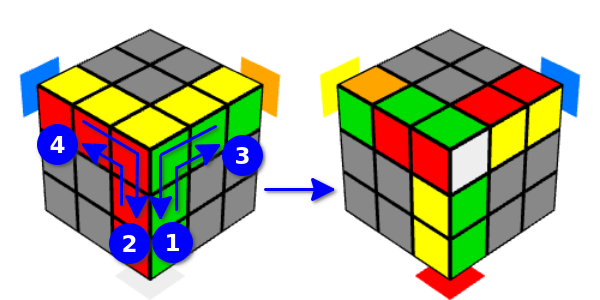
Wir werden diese Option die "rechte Y-Bewegung" nennen (da das Gesicht zuerst nach rechts gedreht wird). In diesem Fall ändert sich die Position der Würfel am Rand, was für diese Flächen und an den oberen Rändern üblich ist. Wenn Sie mit dem Abbiegen von der Vorderseite aus beginnen, sind die gleichen Würfel betroffen. Diese Option wird als „Y-Bewegung nach links“ bezeichnet (da das Gesicht zuerst von links gedreht wird).
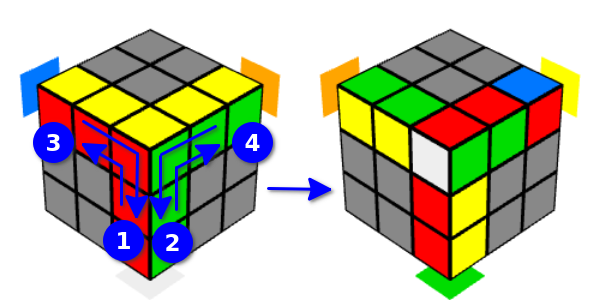
Sie können auch mit „eigenen“ Runden beginnen - es wäre dasselbe, wenn wir den Würfel umdrehen und mit „uns selbst“ Runden beginnen würden. Daher werden wir solche Optionen als „rechts und links umgekehrte Y-Bewegung“ bezeichnen. Bei umgekehrten Y-Bewegungen ist auch die angrenzende Kante betroffen, nicht die obere, sondern die angrenzende untere Kante.
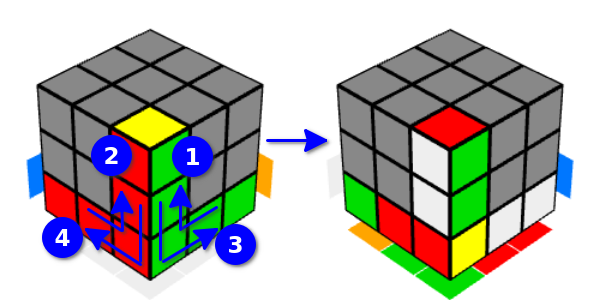
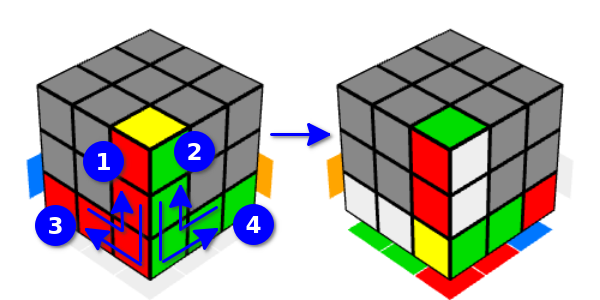
Natürlich gibt es bei all diesen Bewegungen keinen grundsätzlichen Unterschied. Eine solche Vielfalt dient nur der Bequemlichkeit.
Wir listen einige Eigenschaften von Y-Bewegungen auf:
- Die rechte und linke Y-Bewegung sind zueinander invers, d.h. Die Abfolge von rechts und links oder links und rechts ändert den Zustand des Würfels nicht.
- Eine Y-Bewegung bewirkt, dass zwei Eckwürfel auf einer benachbarten Fläche und zwei andere Eckwürfel die Plätze in einem Paar wechseln. Und drei Würfel, die sich in der Mitte der Kanten befinden, bewegen sich in einem Kreis.
- Wie Sie sich vorstellen können, kehren die Eckwürfel nach zwei Bewegungen an ihren Platz zurück. Aber gleichzeitig werden sie gedreht.
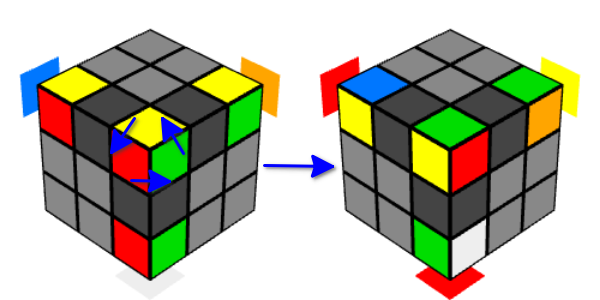
- Und wenn Sie dreimal in zwei Bewegungen ausführen, drehen sich die Würfel dreimal und kehren infolgedessen in ihren ursprünglichen Zustand zurück.
- Die Randwürfel kehren nach einem Zyklus von drei Bewegungen in ihren ursprünglichen Zustand zurück.
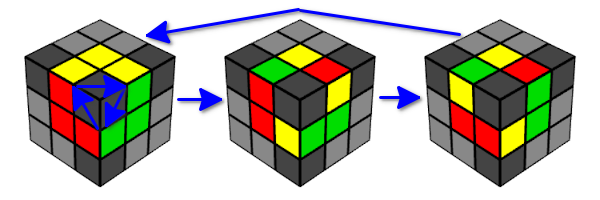
- Wenn Sie also die Y-Bewegung sechsmal hintereinander ausführen, kehrt der Zustand des Würfels zu seinem ursprünglichen Zustand zurück.
- Nach einer Y-Bewegung bewegen sich die Kantenwürfel in die Richtung der ersten Drehung, während sich zwei Würfel anscheinend entlang der entsprechenden Flächen (um ihre Achse) zu drehen scheinen, und der dritte dreht sich ebenfalls, dreht sich jedoch um. Der Würfel, der sich bei der üblichen (nicht invertierten) Y-Bewegung zwischen den oberen Rändern bewegt, kippt um. Wenn Sie mit Kantenwürfeln arbeiten, können Sie die Y-Bewegung entlang derselben Kanten ausführen, indem Sie den Würfel in verschiedene Richtungen drehen, um die gewünschte Würfelumdrehung zu erzielen.
Montagereihenfolge der Würfel
Zunächst werden die beiden unteren Schichten des Würfels zusammengefügt, mit Ausnahme einer vertikalen Kante, die durch diese Schichten verläuft. Wir behalten uns diesen Platz als Handlungsspielraum vor. Der untere Kreuz- und der untere Eckwürfel werden ganz einfach zusammengebaut, aber wenn es Schwierigkeiten gibt, ist es nicht so schwierig, die Y-Bewegung dafür anzupassen oder eine der Anweisungen für eine einfache geschichtete Montage des Würfels zu lesen.

Als nächstes müssen Sie die mittleren Würfel an den vertikalen Kanten (Kanten) sammeln. Drehen Sie dazu die Oberseite mit dem gewünschten Würfel so, dass sie sich auf einer der Seiten neben der Zielkante befindet. Und auch vorübergehend (vergessen Sie dann nicht, zum Platz zurückzukehren), um die Unterseite zu drehen, so dass sich anstelle der Zielkante ein Würfel befindet, den wir speziell nicht zusammengebaut haben. Jetzt können Sie den Würfel mit der Y-Bewegung von der Oberseite an die gewünschte Stelle bewegen. Die Y-Bewegung muss so ausgeführt werden, dass sich dieser Kantenwürfel in die richtige Richtung zur Rippe dreht und sich bei Bedarf umdreht.

Befindet sich der gewünschte Würfel nicht auf der Oberseite, so muss er zuvor auch durch Y-Bewegung von dort „befreit“ werden, ohne erneut zu vergessen, die nicht zusammengebaute Ecke auf der Unterseite zu ersetzen.

Bisher haben wir die beiden unteren Schichten ohne eine Kante gesammelt. Als nächstes müssen wir zwei Kantenwürfel an den oberen Kanten sammeln, die nicht an das grenzen, was wir nicht speziell sammeln. Danach verbleiben von den Kantenwürfeln nur drei nicht zusammengebaute an den Kanten, die den Buchstaben „Y“ bilden: die vertikale, die wir nicht gesammelt haben, und die beiden oberen Kanten, die daneben liegen.

Und natürlich sammeln wir sie mit einer oder mehreren Y-Bewegungen, drehen sie um und platzieren sie an den richtigen Stellen. Hier müssen Sie nur einen Moment bei der Anzahl der Permutationen berücksichtigen, die weiter unten beschrieben wird.
Wenn wir die letzten fünf Kantenwürfel zusammensetzen, müssen wir diesen Buchstaben „Y“ möglicherweise abrollen, um die Y-Bewegung in die andere Richtung auszuführen (andere Flächen entlang dieser Kanten drehen), um die Bewegung der Würfel an andere Stellen mit oder ohne Umdrehung zu erreichen.

An dieser Stelle haben wir einen fast zusammengebauten Würfel, in dem nur die Eckwürfel auf der Oberseite und an der vertikalen Kante, die wir nicht gesammelt haben, nicht gesammelt werden. Mit den nachfolgend beschriebenen Methoden ordnen wir zunächst die Winkel so an, dass sie an ihren Stellen liegen und möglicherweise falsch ausgerichtet sind. Und dann setzen wir sie ein.
Hurra, unser Würfel ist zusammengebaut!
Wir betrachten die Permutationen
Was Sie beachten müssen, wenn wir die letzten fünf Kantenwürfel sammeln. Wenn nur noch drei von ihnen übrig sind, ist es erforderlich, dass sie sich entweder alle an ihrem Platz befinden (möglicherweise auf dem Kopf stehend) oder alle fehl am Platz sind, damit alles mit ihrer Umlagerung innerhalb des Buchstabens „Y“ klappt. Dies liegt daran, dass die Y-Bewegung drei Kantenwürfel gleichzeitig neu anordnet. Wenn wir dies unter dem Gesichtspunkt des paarweisen Austauschs von Würfeln an Orten an benachbarten Kanten betrachten, dann gibt es zwei Austausche (Permutationen). Jetzt sollte klar sein, warum wir in dem Fall, in dem genau zwei Würfel nicht am richtigen Ort sind, diese nicht einsammeln können. Weil wir müssen eine Permutation machen und mit Hilfe von Y-Bewegungen können wir nur eine gerade Anzahl von Permutationen machen.
Was ist in diesem Fall zu tun? Beachten Sie, dass wir, wenn Sie die Fläche des Würfels drehen, vier Kantenwürfel gleichzeitig austauschen, was drei Permutationen entspricht, d. H. eine ungerade Zahl, die wir brauchen. Daraus folgt, dass die Oberseite richtig ausgerichtet sein muss, damit wir die letzten drei Kantenwürfel sammeln können. Wenn die letzten drei Kantenwürfel eine Permutation erfordern, müssen Sie die beiden Kantenwürfel, die bereits auf der Oberseite zusammengesetzt sind, an benachbarten Stellen neu anordnen.
Darüber hinaus können wir vor dem Zusammensetzen der ersten beiden Würfel dieser fünf die Anzahl der Permutationen berechnen, die erforderlich sind, um alle fünf Kantenwürfel in Position zu bringen. Wenn diese Zahl gerade ist, ist die obere Grenze korrekt ausgerichtet. Und wenn es merkwürdig ist, müssen Sie es einmal in eine beliebige Richtung drehen. So können wir diese beiden Würfel sofort an die richtigen Stellen legen.
Mit Eckwürfeln arbeiten
In der letzten Phase der Montage müssen die Eckwürfel an bestimmten Stellen neu angeordnet und gedreht werden. Dazu verwenden wir die zuvor erwähnten Eigenschaften der Y-Bewegung in Bezug auf Eckwürfel. Weil Es ist praktischer, mit Eckwürfeln zu arbeiten, die sich auf der Oberseite befinden. Dazu verwenden wir die umgekehrte Y-Bewegung (sie beginnt mit einer Drehung „von Ihnen weg“). In diesem Abschnitt werden diese Optionen ohne weitere Erläuterung verwendet. Lassen Sie uns sofort bemerken, dass diese Bewegung den Zustand nur eines Würfels auf der Oberseite ändert - dies ist ein eckiger Würfel auf der "benachbarten Kante".
Um die Eckwürfel neu anzuordnen, müssen wir beachten, dass eine einzelne Y-Bewegung (sowohl links als auch rechts) ein Paar Eckwürfel an der "benachbarten Kante" vertauscht und dass die sequentielle Verwendung der linken und rechten Y-Bewegung (oder rechts und links) den gesamten Würfel zurückgibt im Ausgangszustand. Überlegen wir, was passiert, wenn wir die Oberseite zwischen diesen Bewegungen drehen. Wie wir bereits bemerkt haben, ändert sich auf der Oberseite nur ein Eckwürfel, der mit einem Paarwürfel am Rand neu angeordnet wird. In diesem Fall haben wir zwei Eckwürfelwechsel am Rand, aber jedes Mal wird ein anderer Winkel oben eingesetzt, und alle anderen Würfel bleiben unverändert (natürlich müssen Sie immer noch daran denken, die Oberseite in ihren ursprünglichen Zustand zu drehen). So tauschten wir die Plätze von drei Eckwürfeln aus - einen von unten und zwei von oben.
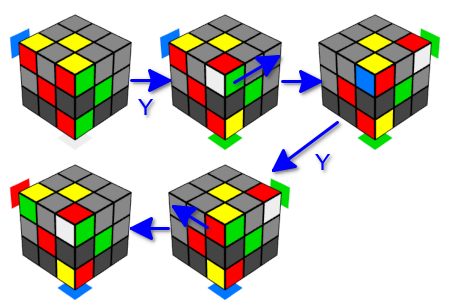
Jetzt beschäftigen wir uns mit der Rotation der Würfel. Verwenden Sie dazu einen ähnlichen Trick. Wir werden zwei aufeinanderfolgende Y-Bewegungen in eine Richtung ausführen. Infolgedessen bleiben die Eckwürfel an Ort und Stelle, ändern jedoch ihre Ausrichtung. Hier interessieren uns zwei Möglichkeiten für eine Bewegungskombination: drei Doppelbewegungen in eine Richtung (links oder rechts) oder eine Doppelbewegung in eine Richtung und eine Doppelbewegung in die entgegengesetzte Richtung. In jeder dieser Optionen kehrt der gesamte Cube in seinen ursprünglichen Zustand zurück. Und wieder werden wir zwischen den Doppelbewegungen den nächsten Winkel einsetzen, den wir anstelle der oberen Ecke der „angrenzenden Rippe“ brauchen. Somit können wir entweder drei Eckwürfel auf einer Fläche in eine Richtung oder zwei Eckwürfel auf einer Fläche in verschiedene Richtungen drehen, ohne den Zustand der verbleibenden Würfel zu ändern. Beachten Sie, dass sich nach einer Doppelbewegung der obere Würfel einer benachbarten Rippe in dieselbe Richtung dreht, in der die erste Y-Bewegung ausgeführt wird.
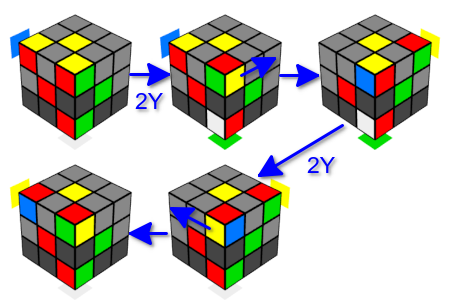
Fazit
Ich weiß nicht, wie es in Ihrem Fall sein wird, aber für mich besteht der Vorteil dieses Algorithmus nicht nur darin, dass er leicht zu merken ist und Sie keine Montageanleitungen stopfen müssen. Aber auch in der Tatsache, dass ich den Würfel jetzt beim Sammeln selbst zusammenbaue und verstehe, was passiert, anstatt den Anweisungen fast mechanisch zu folgen, und das ist viel angenehmer. Was ich dir auch wünsche!