In fast jedem Kartenspiel nach dem Spiel müssen Sie die Karten mischen. Während ich die Karten mische, stellt sich mir immer die Frage: "Schon genug?" Dies ist eine ernste Frage - ich möchte nicht zu viel Zeit damit verbringen, und das Spielen auf einem aufgeladenen Deck macht auch keinen Spaß.

Der Artikel befasst sich mit der Situation.

Shuffle Way

Es gibt coole Möglichkeiten, Karten zu mischen, zum Beispiel Riffle Shuffle.

Ich weiß nicht wie und Pappkarten können nicht so gemischt werden, also mische ich auf einfache Weise, es sieht ungefähr so ​​aus:

Zuerst trenne ich den Teil vom Deck, dann wirf ich den Anteil dieses Teils auf die andere Seite und melde dann den verbleibenden Anteil. Nach meinen Beobachtungen werden Karten genau so oder in der Nähe gemischt. Im Allgemeinen kann es in eine größere Anzahl von Teilen unterteilt werden, aber dies sind bereits Details. Im Artikel werden wir diese Mischmethode analysieren.

Was ist ein zufälliges Kartenlayout?

Das erste, was mir einfiel, war, dass es sich um ein gutes Layout handelt. Es ist wahrscheinlich, dass sich jede Karte an der i-ten Stelle befindet.

Das reicht aber nicht. Wenn Sie zum Beispiel das Deck zerschneiden, es zufällig in zwei Teile teilen und vertauschen, kann die erste Karte eine beliebige Chance sein. Aber gleichzeitig ist dies offensichtlich ein schlechtes Layout: Nach jeder Karte, mit Ausnahme einiger weniger, wird dieselbe Karte ausgegeben, die vor dem "Schneiden" dahinter liegt. Das heißt, die Spieler erhalten "korrelierte" Karten. Im Falle eines Narren wird einer geschlagen, und der andere wird geschlagen, und dies ist kein Zufall.

Ein weiterer Ansatz zur Bestimmung eines guten Layouts besteht darin, dass sich an i + 1 eine Karte befindet, die von der Karte an i-1 unabhängig ist. Sie können es sich so vorstellen: Wenn Sie sich die oberste Karte des Decks ansehen, können Sie nicht erraten, welche Karte als nächstes kommt.

Dieser Ansatz kann auch Probleme haben, die durch die Berücksichtigung großer gemeinsamer Verteilungen gelöst werden, aber für die aktuelle Analyse ist er für uns vollkommen geeignet.

Wie man die "Güte" des Layouts misst

Wir haben das vom vorherigen Spiel übrig gebliebene Deck genommen. Wir nummerieren alle Karten der Reihe nach. Die schlechte Situation ist, wenn es nach dem Mischen an einer Stelle nach der Karte mit der Nummer i eine Karte mit der Nummer i + 1 gibt. Daher werden wir den Anteil der Karten messen, die nach dem Mischen in Ordnung sind.

def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total 

Es ist klar, dass selbst in einem gut gemischten Deck einige Karten in zufälliger Reihenfolge abfallen. Ihr Anteil beträgt im Durchschnitt 1 / (n-1), wobei n die Anzahl der Karten im Stapel ist.

Ergebnisse

Wir berechnen die Wahrscheinlichkeit aufeinanderfolgender Karten für ein Kartenspiel mit 52 Karten in Abhängigkeit von der Anzahl der Mischungsiterationen.

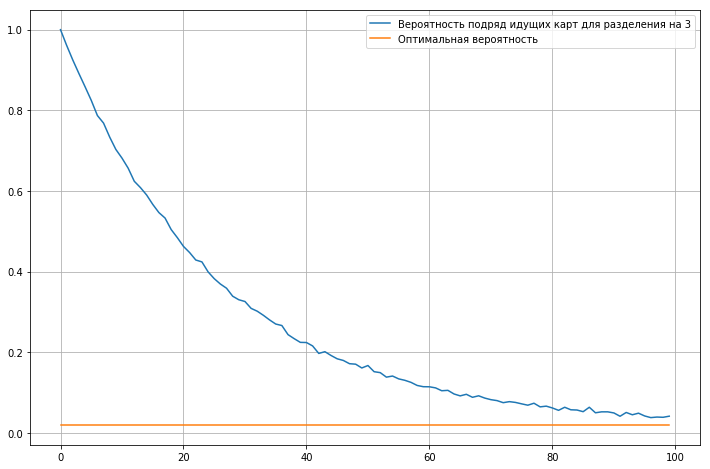
Die Grafik zeigt, dass die Wahrscheinlichkeit aufeinanderfolgender Karten selbst nach Hunderten von Iterationen etwa doppelt so hoch ist wie die ideale Wahrscheinlichkeit.

 import random def two_split_shuffle(a): s1 = random.randint(1,len(a)-1) s2 = random.randint(1,len(a)-1) s_min = min(s1, s2) s_max = max(s1, s2) p1 = a[:s_min] p2 = a[s_min:s_max] p3 = a[s_max:] return p3 + p2 + p1 def shuffle_n(a, f, n): for _ in range(n): a = f(a) return a def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total def expected(f, n = 100): s = 0 for _ in range(n): s += f() return s / n def get_expected_next_stat(shuf, n, cards): return expected(lambda: next_stat(shuffle_n(range(cards), shuf, n))) cards = 52 x = range(100) y = map(lambda i: get_expected_next_stat(two_split_shuffle, i, cards), x) import matplotlib.pyplot as plt %matplotlib inline plt.figure(figsize=(12,8)) plt.plot(x, y, label = u'       3') plt.plot(x, [1./(cards-1)] * len(x), label = u' ') plt.grid() plt.legend() 

Im Allgemeinen können wir davon ausgehen, dass 60 Iterationen die optimale Menge sind, weniger ist definitiv schlecht. Ich mache ungefähr 16-17 Iterationen in 30 Sekunden. Dies bedeutet, dass ein normaler Shuffle fast zwei Minuten dauert .

Meine Freunde und ich mischen nie so viel Karten. Und das bedeutet, dass unser Spiel sehr stark von der Balance des letzten Spiels beeinflusst wird.

Sei vorsichtig :)