Hallo allerseits, mein Name ist Alexander und ich bin Datenwissenschaftler bei Clain. Wir analysieren Blockchain-Transaktionen auf ihre Zugehörigkeit zu kriminellen Handlungen wie Auszahlungen, Diebstahl, Terrorismusfinanzierung und dergleichen.
Die Vorschriften für Kryptowährungen werden jedes Jahr verschärft, und jetzt müssen Unternehmen die AML \ KYC-Richtlinien einhalten. Etwa das Gleiche hat die Firma Elliptic, die Anfang August 2019 einen etikettierten Datensatz mit 200.000 Bitcoin-Transaktionen veröffentlichte.
Der Hauptzweck ihrer Veröffentlichung ist es, der Crypto-Community echte Daten zu liefern, um neue Ansätze zur Erkennung zweifelhafter Transaktionen zu testen, indem sowohl eine Reihe von Standardattributen (Anzahl der Ein- und Ausgaben, Übertragungen, Übertragungen an Miner usw.) als auch die Topologie des auf diesen Transaktionen basierenden Diagramms verwendet werden . Der Datensatz ist anonymisiert und weist 167 Attribute auf. Alle von ihnen haben einen Mittelwert von Null und eine Einheitsvarianz mit Ausnahme des ersten, der die Kennung ist, und des zweiten, der die Zeit von 1 bis 49 kennzeichnet, die den Komponenten des Transaktionsgraphen entspricht.
Mit der Datei elliptic_txs_edgelist.csv können Sie ein gerichtetes Diagramm erstellen und den eingehenden und ausgehenden Grad jeder txId-Transaktion berechnen. Auf diese Weise können Sie ungefähr (da das Diagramm aus der gesamten Blockchain entfernt wird und ein Teil der Verbindungen verloren geht) die Anzahl der Absender- und Empfängeradressen für jede Transaktion schätzen. Benennen Sie in der Platte elliptic_txs_features.csv die Spalten in V1 - V167 um und ersetzen Sie V1 sofort durch txId, V2 durch elliptic_time. Einige Attribute korrelieren besser als andere mit dem Wert des eingehenden und ausgehenden Grades des Graphen: cor (out-degree, V16) = 0,689, cor (out-degree, V7) = 0,680, cor (in-degree, V6) = 0,589, cor (in-degree, V6) = 0,589. Grad, V8) = 0,582. Schauen wir uns diese Variablen an.
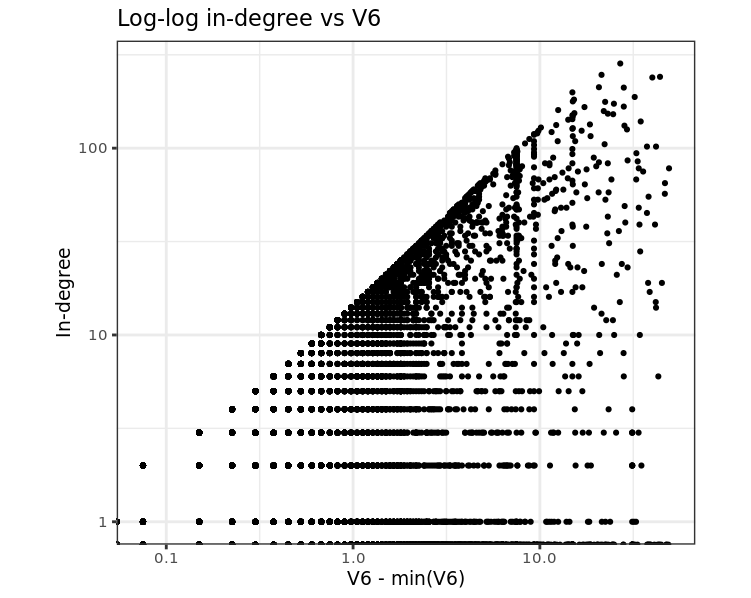
Scatterplot-Offset V6-Variable und eingehender Graphengrad von elliptic_txs_edgelist
Laut Diagramm gibt es für jeden In-Grad-Wert eine Obergrenze für V6-Werte. Wenn Sie V6 sortieren und die Differenz zwischen ähnlichen Werten ermitteln, ändert sich dies als Ganzzahl multipliziert mit einer Konstante:

Eindeutige Werte der Änderung von sortiertem V6 (diff_V6), der angetroffenen Frequenz (Freq) von diff_V6-Werten und des Verhältnisses von diff_V6 zu dem Minimalwert von diff_V6.
In der V6-Änderungstabelle können Sie sehen, dass 0.075038 viel häufiger auftritt als die übrigen Werte und wahrscheinlich mit einer Änderung des Grades um 1 verbunden ist. Da die Mindestanzahl der Einträge in einer Transaktion 1 beträgt (wenn es sich nicht um eine Coinbase-Transaktion handelt), schreiben wir:
input_count_V6 = (V6 - min (V6)) / min (diff_V6) + 1.
Nach einer ähnlichen Analyse für V7, V8, V16:
- input_count_V6 = 13.3266685112665 * V6 + 2.62544842444139,
- input_unique_count_V8 = 11.9243179897452 * V8 + 2.34747189219164,
- output_count_V7 = 50.3777694891647 * V7 + 4.21030186142152,
- output_unique_count_V16 = 49.3957564403755 * V16 + 4.121809499973.
Hier ist input_count_V6 die Gesamtzahl der Einträge in der Transaktion, input_unique_count_V8 die Anzahl der eindeutigen Einträge in der Transaktion, output_count_V7 die Anzahl der Exits aus der Transaktion und output_unique_count_V16 die Anzahl der eindeutigen Exits.
Es kann sich die Frage stellen, warum V6 und nicht V8 input_count zugeordnet sind. Die Antwort ist einfach: Immer input_count> = input_unique_count. Durch Ersetzen der Werte von V6 und V8 durch elliptic_txs_features.csv in den angegebenen Formeln können wir sicherstellen, dass die Ungleichung (13.3266685112665 V6 + 2.62544842444139)> = (11.92431879897 Korrelation zwischen V6, V8, input_count und input_unique_count. Gleiches gilt für output_count und output_unique_count.
Sobald Sie die Anzahl der Ein- und Ausgänge sowie die Anzahl der eindeutigen Ein- und Ausgänge gefunden haben, können Sie Transaktionen finden, bei denen Kombinationen dieser Zahlen im gesamten Verlauf von Bitcoin nur einmal vorkommen (bis zur Veröffentlichung des elliptischen Datensatzes). Auf diese Weise können Sie für jeden elliptic_time-Wert eindeutige Transaktionen und ungefähre Zeiten ermitteln:
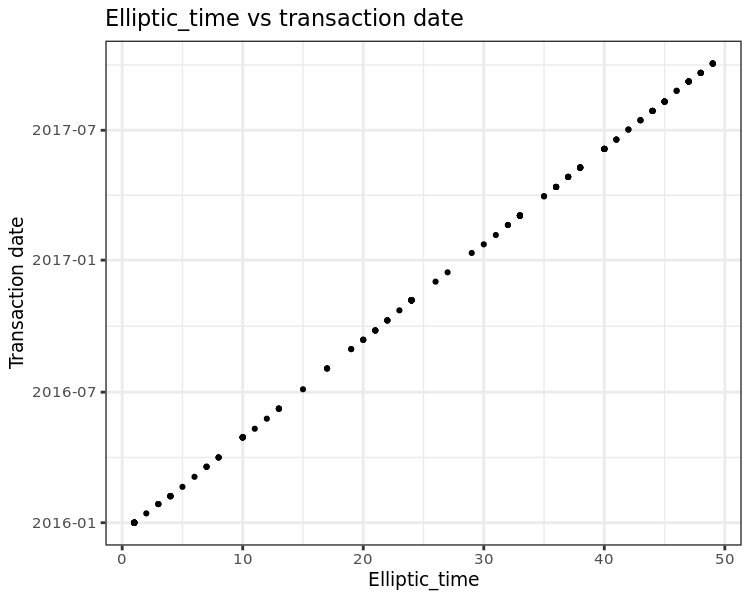
Datum der eindeutigen Transaktionen, die für jede elliptische_Zeit gefunden wurden.
Die obige Grafik zeigt, dass das Datum linear von elliptic_time abhängt:
approx_time = 1450468509.80488 + 1155672.19512195 * elliptic_time.
Hier ist approx_time eine ungefähre Unixzeit für jede elliptische Zeit. Und da elliptic_time von 1 bis 49 variiert, ändert sich das ungefähre Datum vom 01.01.2016 bis zum 04.10.2017 in Schritten von 1155672.19512195 / 3600/24 = 13.37584 Tagen.
Angesichts der zeitlichen Beschränkungen möglicher Transaktionen und Kombinationen einer eindeutigen Anzahl von Ein- und Ausgängen finden Sie 189 Transaktionen, die für diese Bedingungen geeignet sind und in der gesamten Bitcoin-Blockchain nur einmal vorkommen. Beispielsweise gibt es nur eine Transaktion mit 1 Eingang und 13107 Ausgängen - dd9f6bbf80ab36b722ca95d93268667a3ea6938288e0d4cf0e7d2e28a7a91ab3.
Jetzt finden Sie in Satoshi weitere Merkmale von Transaktionen, z. B. Gebühr, sowie das gesamte Input- (total_in_value) und Output-Volumen (total_out_value). Die Korrelationssuche und die lineare Regression helfen dabei, dies schnell zu erreichen. Ich werde nur die endgültigen Formeln angeben:
- fee_V4 = 81341.4537626213 + 386323.710952989 * V4,
- total_out_value_V3 = 2742460603.92287 + 15853961614.9796 * V3.
Wir finden den benötigten Wert total_in_value aus der Gleichheit:
total_in_value = total_out_value + fee.
Mit den insgesamt gefundenen Informationen können wir 92,9% aller Elliptic-Dataset-Transaktionen identifizieren. Der andere Teil kann aufgedeckt werden, wenn Sie das Transaktionsdiagramm aus elliptic_txs_edgelist.csv verwenden und es mit einem Diagramm vergleichen, das auf vielen geeigneten Transaktionen mit ihren in der Blockchain aufgezeichneten Verbindungen basiert. Dies fügt weitere 6,6% hinzu.
So lassen sich 99,5% aller anonymen Transaktionen leicht offenlegen, die verbleibenden 0,5% können ebenfalls identifiziert werden, aber die Zeit, die für ihre Deanonymisierung aufgewendet wird, ist wahrscheinlich mit der Zeit vergleichbar, die für den bereits offengelegten Teil der Transaktionen aufgewendet wird. Sie können den deanonymisierten Datensatz hier sehen . Und hier sind die ursprünglichen elliptischen Daten.