Newton-Cotes-Methoden sind eine Kombination von ungefähren Integrationstechniken basierend auf:
- Aufteilen des Integrationsintervalls in gleiche Intervalle;
- Annäherungen des Integranden an ausgewählte Intervalle durch Polynome;
- Finden der Gesamtfläche des erhaltenen gekrümmten Trapezes.
Dieser Artikel behandelt verschiedene Newton-Cotes-Methoden:
- Trapez-Methode;
- Simpsons Methode;
- Romberg-Methode.
Trapez-Methode
Die Trapezmethode ist die einfachste der in Betracht gezogenen. Nehmen Sie als Beispiel das folgende Integral:
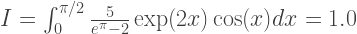
Die Genauigkeit der Approximation hängt von der Anzahl N der Segmente ab, in die das Integrationsintervall unterteilt ist. Somit ist die Spaltlänge:
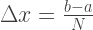
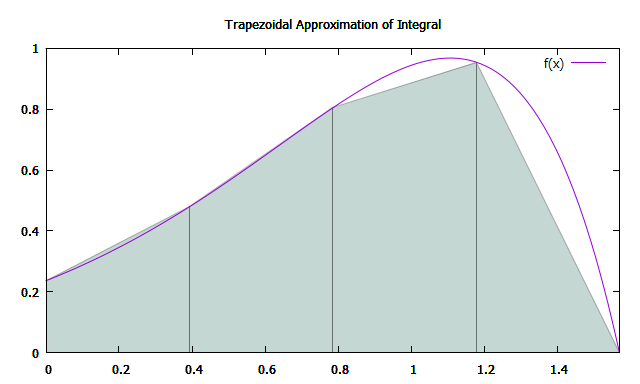
Die Fläche des Trapezes kann nach folgender Formel berechnet werden:
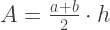
Zusammenfassend wird der ungefähre Wert des Integrals durch die Formel berechnet:
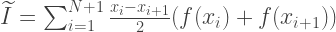
Die Funktion, die das Integral nach der Trapezmethode berechnet, sollte 4 Parameter annehmen:
- Grenzen des Integrationssegments;
- Integrandenfunktion;
- die Anzahl N der Intervalle der Partition.
double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double trapezoidal_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2)); } return trapezoidal_integral; }
Simpson-Methode
Die Simpson-Methode besteht darin, das Interpolationspolynom zweiten Grades der Funktion f (x) mit den Interpolationsknoten a, b und m = (a + b) / 2 - Parabeln p (x) zu integrieren. analog zur Trapezmethode), auf die jeweils die Simpson-Methode angewendet wird.
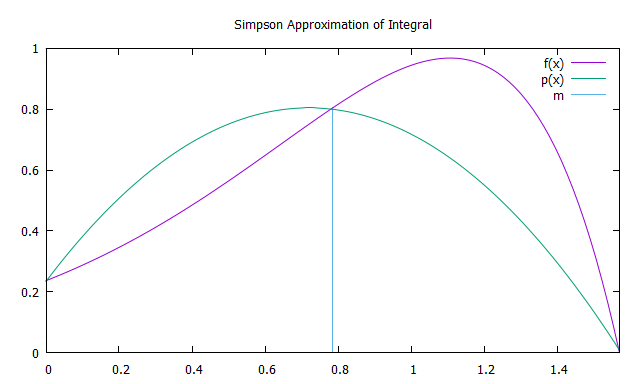
Die Fläche der Parabel ergibt sich aus der Summe der Flächen von 6 gleich breiten Rechtecken. Die Höhe des ersten von ihnen sollte gleich f (a) sein, vom dritten bis zum fünften - f (m), dem sechsten - f (m). Die Näherung nach der Simpson-Methode ergibt sich also aus der Formel:
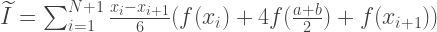
double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double simpson_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2)); } return simpson_integral; }
Romberg-Methode
Sei T (x) die durch die Trapezmethode mit Schritt x erhaltene Integralapproximation. Wir erhalten 3 solcher Näherungen, die die Schrittgröße bei jeder Berechnung um das 2-fache reduzieren.

Wir konstruieren nun eine zur y-Achse symmetrische Parabel, die durch die Punkte T (1) und T (1/2) verläuft, um die erhaltenen Werte für x zu extrapolieren, die gegen 0 tendieren.
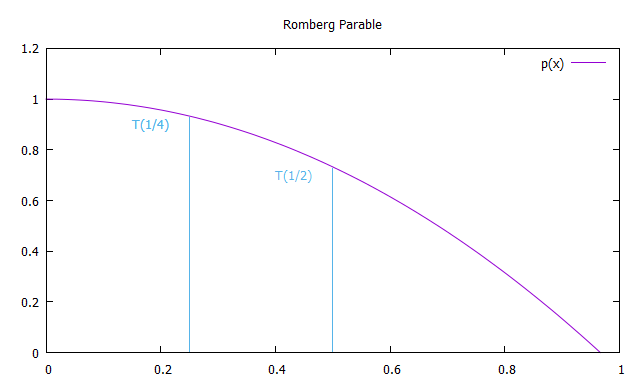
Daher entspricht jedes Mitglied der ersten Spalte R (n, 0) der Romberg-Näherungen den nach der Trapezmethode erhaltenen Lösungen, und jede Lösung der zweiten Spalte von R (n, 1) entspricht der Simpson-Methode. So lauten die Formeln für die ungefähre Integration nach der Romberg-Methode:
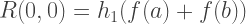
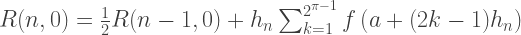
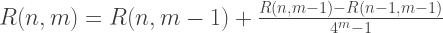
C ++ Implementierung:
std::vector<std::vector<double>> rombergIntegral(double a, double b, size_t n, const std::function<double (double)> &f) { std::vector<std::vector<double>> romberg_integral(n, std::vector<double>(n)); romberg_integral.front().front() = trapezoidalIntegral(a, b, 1, f); double h = ba; for(size_t step = 1; step < n; step++) { h *= 0.5; double trapezoidal_integration = 0; size_t stepEnd = pow(2, step - 1); for(size_t tzStep = 1; tzStep <= stepEnd; tzStep++) { const double deltaX = (2*tzStep - 1)*h; trapezoidal_integration += f(a + deltaX); } romberg_integral[step].front() = 0.5*romberg_integral[step - 1].front() + trapezoidal_integration*h; for(size_t rbStep = 1; rbStep <= step; rbStep++) { const double k = pow(4, rbStep); romberg_integral[step][rbStep] = (k*romberg_integral[step][rbStep-1] - romberg_integral[step-1][rbStep-1])/(k-1); } } return romberg_integral; }