Die Farbe des Mondes und der Sonne aus dem All in Bezug auf RGB und Farbtemperatur

Es scheint, dass die Frage nach der Farbe von Mond und Sonne aus dem Weltraum für die moderne Wissenschaft so einfach ist, dass es in unserem Jahrhundert überhaupt kein Problem mit der Antwort geben sollte. Bei der Beobachtung aus dem Weltraum geht es um Farben, da die Atmosphäre durch Rayleigh-Lichtstreuung eine Farbveränderung hervorruft. "Sicherlich irgendwo in der Enzyklopädie darüber im Detail, in Zahlen ist es schon lange geschrieben worden", werden Sie sagen. Versuchen Sie nun, im Internet nach Informationen zu suchen. Ist passiert? Höchstwahrscheinlich nein. Das Maximum, das Sie finden werden, sind ein paar Worte über die Tatsache, dass der Mond einen bräunlichen Farbton hat und die Sonne rötlich ist. Sie werden jedoch keine Informationen darüber finden, ob diese Farbtöne für das menschliche Auge sichtbar sind oder nicht, insbesondere die Bedeutung der Farben in RGB oder zumindest die Farbtemperaturen. Aber Sie werden eine Reihe von Fotos und Videos finden, auf denen der Mond aus dem Weltraum absolut grau ist, hauptsächlich auf Fotos des amerikanischen Apollo-Programms, und auf denen die Sonne aus dem Weltraum weiß und sogar blau dargestellt ist.

Besonders meine persönliche Meinung ist nichts anderes als eine Konsequenz des Eingreifens der Politik in die Wissenschaft. Schließlich stehen die Farben des Mondes und der Sonne aus dem All in direktem Zusammenhang mit den Flügen der Amerikaner zum Mond.

Ich suchte in vielen wissenschaftlichen Artikeln und Büchern nach Informationen über die Farbe des Mondes und der Sonne aus dem All. Glücklicherweise stellte sich heraus, dass sie zwar keine direkte Antwort auf RGB haben, jedoch vollständige Informationen über die spektrale Dichte der Sonnenstrahlung und das Reflexionsvermögen des Mondes im gesamten Spektrum vorliegen. Dies ist völlig ausreichend, um genaue Farben in RGB-Werten zu erhalten. Sie müssen nur sorgfältig kalkulieren, was ich tatsächlich getan habe. In diesem Artikel teile ich Ihnen die Ergebnisse der Berechnungen mit und erzähle Ihnen natürlich ausführlich über die Berechnungen selbst. Und Sie werden den Mond und die Sonne aus dem All in echten Farben sehen!

Ich habe die Berechnungen im Mathcad-Programm durchgeführt und dementsprechend werden die Codefragmente in der eingebauten Programmiersprache vorliegen, die für alle Pseudo-Codes durchaus als verständlich geeignet ist.

Gleichzeitig werde ich Ihnen im Detail sagen, was das RGB-Farbmodell ist, mit dem Sie, wie ich finde, alle vertraut sind. Diese Frage ist auch nicht ganz einfach. Versuchen Sie beispielsweise, die folgenden zwei Fragen zu beantworten. Lassen Sie die Farbe auf rgb (120, 80, 100) eingestellt sein .
1) Welche RGB-Werte haben eine Farbe, die zweimal dunkler als die angegebene ist?
2) Was sind die RGB-Werte in Grau bei gleicher Helligkeit wie angegeben?
Es scheint, dass es Denken gibt, das im ersten Fall durch 2 geteilt wird, dh rgb (60,40,50) und im zweiten Fall gemittelt wird, dh rgb (100,100,100) . Leider sind die richtigen Antworten: 1) rgb (86.56.71) ; 2) rgb (92,92,92) . Sie werden herausfinden, warum die Antworten einfach so sind.

Sprechen Sie auch über die Farbtemperatur und wie man sie berechnet.

XYZ-Farbraum

XYZ ist ein Master-Farbmodell, das 1931 von der Internationalen Beleuchtungsorganisation CIE (International Commission on Illumination) im engeren mathematischen Sinne definiert wurde. Modell CIE XYZ ist ein Master-Modell fast aller anderen Farbmodelle, die in technischen Bereichen verwendet werden. Die XYZ-Farbe wird wie folgt eingestellt:

$$

$$X = \ int _ {390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {x}} (\ lambda) \, d \ lambda \\ Y = \ int _ { 390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda \\ Z = \ int _ {390 \, nm} ^ { 830 \, nm} I (\ lambda) \, {\ overline {z}} (\ lambda) \, d \ lambda$$

wo $$$I (\ lambda)$ - die spektrale Dichte eines beliebigen energiephotometrischen Wertes (z. B. Strahlungsfluss, Energiehelligkeit usw. in absoluten oder relativen Zahlen) über den Wellenlängenbereich von 390 bis 830 nm (dies entspricht 2006, 1931 war der Bereich von 380 bis 780 nm ); $$${\ overline {x}} (\ lambda)$ , $$${\ overline {y}} (\ lambda)$ , $$${\ overline {z}} (\ lambda)$ - Farbanpassungsfunktionen. Darüber hinaus entspricht die Y-Koordinate, was für uns wichtig ist, der visuellen Helligkeit des Signals.

Ich habe diese Farbanpassungsfunktionen hier heruntergeladen: [ 1 ]. Dort werden die Farbanpassungsfunktionen für ein 2-Grad- und ein 10-Grad- Sichtfeld definiert. Ich habe beschlossen, für beide Fälle Berechnungen durchzuführen, die Ergebnisse zu vergleichen und sicherzustellen, dass die Farbkoordinaten erwartungsgemäß geringfügig voneinander abweichen. Natürlich habe ich die Daten der Funktionen mit der maximalen Auflösung der bereitgestellten verwendet, dh mit einem Schritt von 0,1 nm . Die Diagramme der Farbanpassungsfunktionen lauten wie folgt:



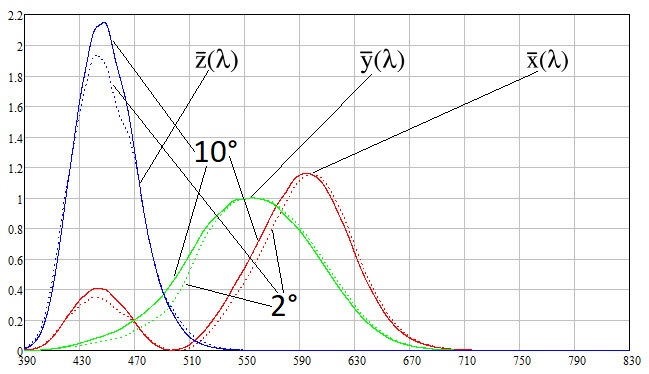
Aus den Diagrammen ist ersichtlich, dass oberhalb von 710 nm die Funktionen in dem Sinne vernachlässigbar werden, dass bei der Beobachtung von Farben in der Nähe von Weiß die Spektraldichte im Bereich oberhalb von 710 nm fast keinen Beitrag leistet. Wir wissen zwar, dass sichtbares Licht im Bereich bis zu 780 nm liegt , aber wir müssen verstehen, dass es sich um monochromatische Strahlung handelt. Ich habe das alles mit der Tatsache zu tun, dass ich bei Berechnungen in einigen Fällen die fehlenden Daten zum Reflexionsvermögen des Mondes nur für den Bereich extrapolieren musste, in dem die Funktionen der Farbanpassung im Wesentlichen klein sind. Ein möglicher Extrapolationsfehler führt daher nicht zu einem merklichen Fehler in den berechneten Farben.

Ich berechne die obigen Integrale nach der Trapezregel :


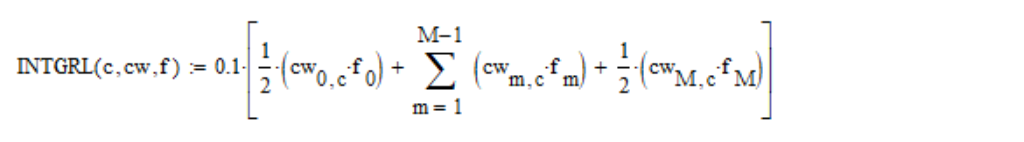
wobei c - die Koordinatennummer des Farbraums ist (1, 2, 3 für X, Y, Z); cw - ist eine Tabelle mit Farbanpassungsfunktionen; f - ist die spektrale Dichte; M = (830-390) /0.1=4400 - die Anzahl der Rasterschritte.

Die korrekten Farbanpassungsfunktionen haben die Eigenschaft, dass die Fläche unter allen drei Kurven gleich ist:

$$

$$\ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {x}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {y}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {z}} (\ lambda) \, d \ lambda$$

Dies erfolgt so, dass das einheitliche Spektrum die gleichen XYZ-Koordinatenwerte aufweist. Überprüfen Sie, ob diese Eigenschaft enthält:


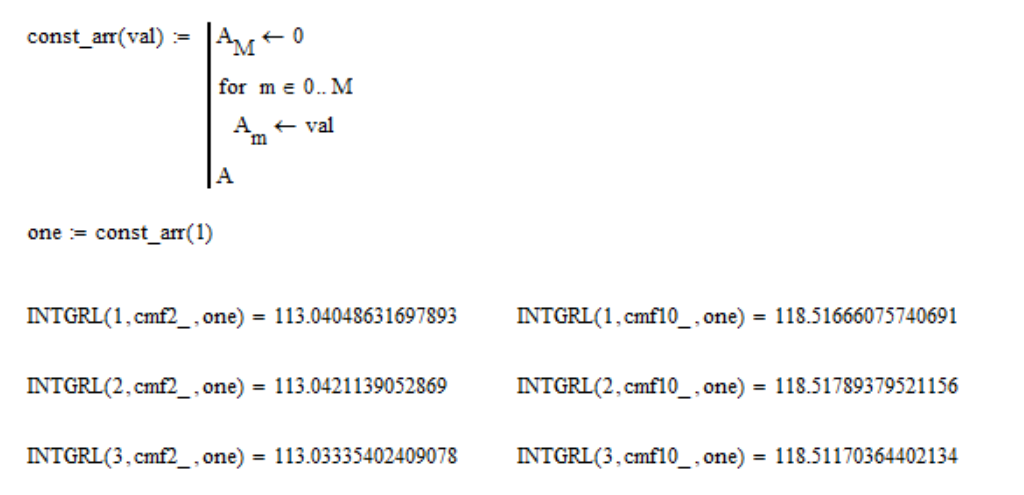
wobei "eins" - ein Array von 1 ist; cmf2_ und cmf10_ - sind Farbanpassungsfunktionstabellen für ein Sichtfeld von 2 Grad bzw. 10 Grad . Wie Sie sehen können, wird die Eigenschaft mit einer Genauigkeit von ungefähr 0,01% ausgeführt , was ziemlich gut ist. Renormieren Sie dennoch die Funktionen für die Wiedergabetreue:

Helligkeitsnormalisierung

Betrachten Sie die Arbeit einer Digitalkamera. Das Hauptelement einer Digitalkamera ist eine Matrix, die aus Photosensoren besteht. Wenn ein Bild auf eine Matrix projiziert wird, sammelt sich in jedem seiner Fotosensoren eine elektrische Ladung an, die proportional zur Strahlungsenergie des Fotosensors ist. Photosensoren erfassen die Helligkeit des Bildelements, ohne Informationen über seine Farbe zu enthalten. Zur Farbinformation wird die Matrix der Photosensoren von Miniaturfiltern überdeckt. Diese Filter übernehmen die Funktion der Farbanpassung. Jedes Pixel besteht aus mehreren Fotosensoren, die in der Menge verschiedener Lichtfilter zusammengefasst sind.

Also als Funktion $$$I (\ lambda)$ wir sollten die spektrale Dichte der Strahlungsenergie eines Pixels nehmen. Eine solche spektrale Dichte kann dargestellt werden als

$$

$$I (\ lambda) = coef \ cdot Illumination (\ lambda) \ cdot Albedo (\ lambda)$$

wobei die Beleuchtung - die spektrale Dichte der Lichtquelle ist; Albedo - das Reflexionsvermögen der Oberfläche des fotografierten Objekts; Koeffizient - ist ein bestimmter konstanter Koeffizient, der durch die Belichtungszeit, die Blende, den Abstand von der Lichtquelle zum zu fotografierenden Objekt und andere Faktoren bestimmt wird. Das Reflexionsvermögen bezieht sich auf die sichtbare Albedo , die als das Verhältnis der Helligkeit eines durch einen parallelen Strahl beleuchteten Flächenelements zur Helligkeit der senkrecht zu den Strahlen liegenden, absolut weißen Fläche definiert ist.

Stellen Sie sich nun vor, wir erledigen die Arbeit des Belichtungsmessers, mit dem der Fotograf die Verschlusszeit und die Blende an der Kamera einstellt. Mit anderen Worten, wir müssen einen Coef- Wert wählen, damit das Bild eine normale Helligkeit aufweist, nicht zu dunkel und nicht zu hell. Stellen Sie sich vor, dass sich hinter dem zu fotografierenden Objekt der absolut weiße Bildschirm befindet. Die Reflektivitätsalbedo eines solchen Bildschirms ist definitionsgemäß bei allen Wellenlängen gleich 1. Stellen Sie den Wert von coef so ein, dass die visuelle Helligkeit Y dieses Bildschirms gleich 1 ist. Warum 1? Denn im RGB-Farbmodell ist der maximal mögliche Helligkeitswert 1, der mit rgb (255,255,255) , also mit Weiß, erreicht wird. Ich werde später darüber erzählen. Da normale Körper eine dunklere Farbe haben als der absolut weiße Bildschirm, ist die Helligkeit der Bilder normal. Aus diesen Überlegungen erhalten wir den folgenden Ausdruck für coef :

$$

$$coef = \ frac {1} {\ int _ {390 \, nm} ^ {830 \, nm} Beleuchtung (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda}$$

Es ist zu beachten, dass eine solche Normalisierung nicht garantiert, dass der Wert jeder RGB-Koordinate kleiner oder gleich 255 ist. Wenn Sie beispielsweise den absolut weißen Bildschirm mit einer roten Lichtquelle fotografieren, wird die RGB-Farbe ausgeblendet die Waage.

So berechne ich die Koordinatenwerte des XYZ-Farbraums wie folgt:


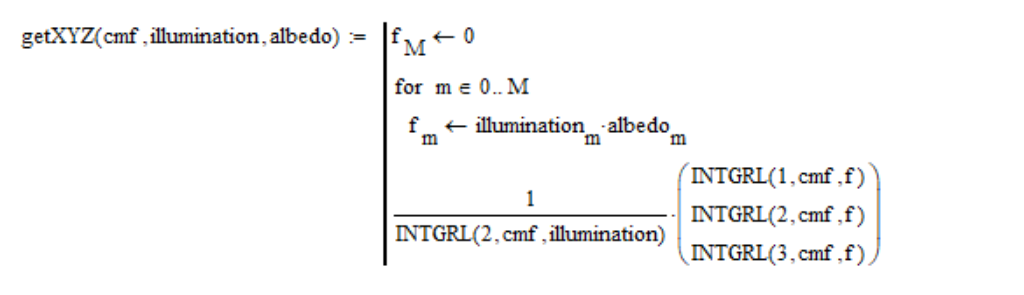
Wir müssen irgendwie die Farbe der Sonne ausdrücken. Wir können es nicht direkt fotografieren, und in unserem mathematischen Modell haben wir einen solchen Extremfall nicht vorhergesehen. Natürlich müssen wir die absolut weiße Oberfläche fotografieren, die von der Sonne beleuchtet wird. Da die Sonne aus dem All einen rötlichen Farbton hat, verschwindet, wie gesagt, die Farbe des absolut weißen Bildschirms von der Skala. Deshalb müssen wir die Oberfläche dunkler nehmen. Ich habe empirisch festgestellt, dass wir Weißbuch mit einer Albedo von 0,91 nehmen müssen. Mehr Albedo kann nicht genommen werden, beginnt die Waage zu verlassen. Um die Farbe der Sonne zu erhalten, setze ich einfach den Albedo- Wert bei allen Wellenlängen in der obigen Formel auf 0,91:

sRGB-Farbraum

Der häufigste Farbraum beim RGB-Modell ist sRGB. Wenn von RGB ohne Klärung die Rede ist, ist daher der sRGB-Farbraum der Standard für die Darstellung des Farbspektrums mit dem RGB-Modell. Dieser Standard wurde 1996 vom International Color Consortium (ICC) erstellt, um die Verwendung des RGB-Modells in Monitoren, Druckern und Internetseiten zu vereinheitlichen. Analysieren wir diesen Standard, dessen Beschreibung unter [ 2 ] verfügbar ist.

Die Umwandlung von XYZ in sRGB erfolgt in drei Schritten. Zuerst werden XYZ-Koordinaten in lineare RGB-Koordinaten konvertiert, dann werden lineare Koordinaten in nichtlineare RGB-Koordinaten konvertiert und am Ende werden nichtlineare Koordinaten in 8-Bit-RGB-Koordinaten konvertiert, die tatsächlich die Koordinaten von sind sRGB-Farbraum.

Die Konvertierung von XYZ-Koordinaten in lineare RGB-Koordinaten sieht wie folgt aus:



und das Gegenteil ist:



Ich frage mich, woher diese seltsamen Zahlen in quadratischen Matrizen stammen. Und sie kamen aus der Empfehlung der ITU-R BT.709 [ 3 ]. Bezeichnen Sie die erste Quadratmatrix mit XYZ_to_RGB und die zweite mit RGB_to_XYZ . Offensichtlich sind sie gegenseitig umgekehrt. Empfehlung ITU-R BT.709 spezifiziert die Anforderungen an die zweite Matrix. Aus diesen Anforderungen können Sie die zweite Matrix eindeutig berechnen, und die erste ist gleich der inversen Matrix der zweiten.

Wir stellen folgende Funktionen vor:

$$

$$XYZ (R, G, B) = RGB \ _bis \ _XYZ \ cdot {\ begin {bmatrix} R \\ G \\ B \ end {bmatrix}} \\ W (R, G, B) = XYZ_1 (R , G, B) + XYZ_2 (R, G, B) + XYZ_3 (R, G, B) \\ xy (R, G, B) = \ frac {1} {W (R, G, B)} \ cdot {\ begin {bmatrix} XYZ_1 (R, G, B) \\ XYZ_2 (R, G, B) \ end {bmatrix}}$$

Dann haben die Anforderungen der Empfehlungen ITU-R BT.709 folgende Form:

$$

$$xy (1,0,0) = {\ begin {bmatrix} 0.64 \\ 0.33 \ end {bmatrix}}, \; xy (0,1,0) = {\ begin {bmatrix} 0.30 \\ 0.60 \ end {bmatrix}}, \; xy (0,0,1) = {\ begin {bmatrix} 0.15 \\ 0.06 \ end {bmatrix}} \\ xy (1,1,1) = {\ begin {bmatrix} 0.3127 \\ 0.3290 \ end {bmatrix }}$$

Wir haben 8 Gleichungen, wenn wir 9 unbekannte Elemente der RGB_to_XYZ- Matrix haben, d. H. Eine weitere Gleichung fehlt. Und fehlende Gleichung ist implizit gegeben, ich musste selbst davor raten. Die Essenz dieser Gleichung ist, dass für weiße Farbe die visuelle Helligkeit Y gleich 1 sein sollte:

$$

$$XYZ_2 (1,1,1) = 1$$

Ich habe die genaue Lösung dieser Gleichungen in rationalen Zahlen gefunden:


Wenn Sie die Zahlen in meinem Ergebnis auf vier Dezimalstellen nach dem Punkt runden, erhalten Sie diese seltsamen Zahlen im Standard des International Color Consortium. In meinen Berechnungen verwende ich keine gerundeten Matrizen, sondern die oben genannten exakten (soweit dies Gleitkommazahlen mit doppelter Genauigkeit zulassen).

Die linearen Koordinaten von RGB basierend auf der Tabelle der Farbanpassungsfunktionen (cmf), der spektralen Strahlungsdichte (Beleuchtung) und des Reflexionsvermögens (Albedo) berechne ich wie folgt:



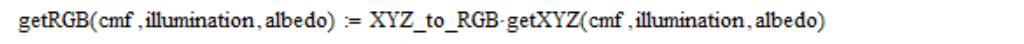
Ich verwende auch lineare Koordinaten RGB, gemittelt über das 2-Grad- und 10-Grad- Sichtfeld:



Aus den linearen Koordinaten von RGB wird die visuelle Helligkeit Y mit der folgenden Formel berechnet (standardmäßig werden Mathcad-Arrays beginnend mit dem Nullelement nummeriert):


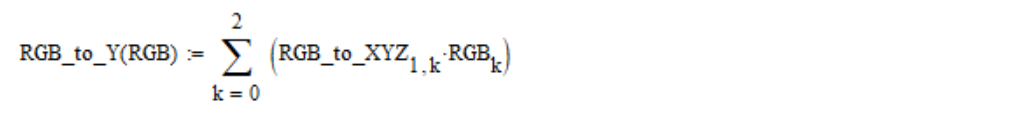
Wir bauen den Standard weiter auseinander. Jede lineare Koordinate des RGB wird mit der nichtlinearen Funktion lin2bit in eine nichtlineare Koordinate konvertiert, und zurück zu bit2lin. Diese werden wie folgt definiert:


Die Grafiken dieser Funktionen sehen folgendermaßen aus:



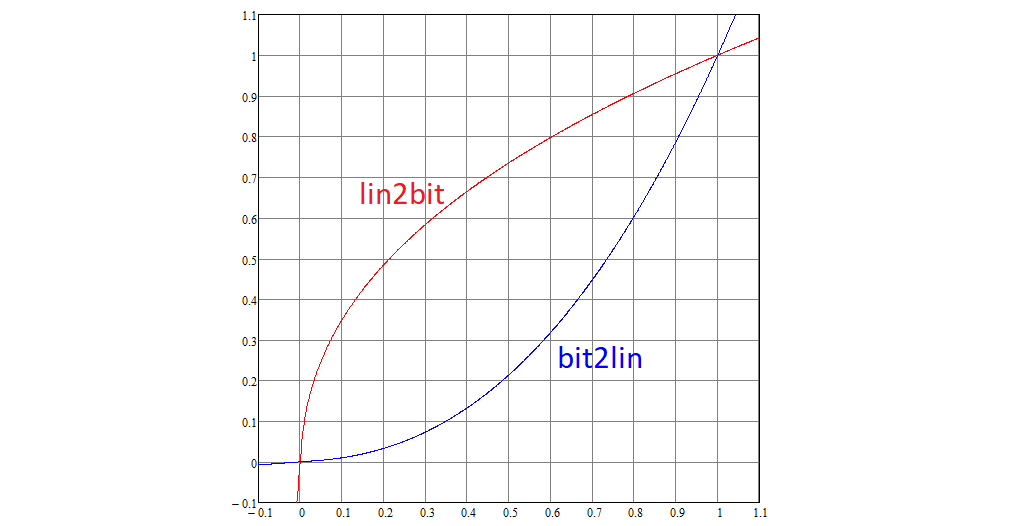
Beachten Sie, dass 0 zu 0, 1 zu 1 konvertiert wird.

Am Ende werden die nichtlinearen Koordinaten von RGB durch Multiplikation mit 255 in 8-Bit konvertiert, gefolgt von einer Rundung auf ganzzahlige Zahlen.

Daher habe ich die folgenden Funktionen zum Konvertieren von linearen RGB-Koordinaten in 8-Bit und zurück definiert:

Jetzt sind wir bereit, das Problem aus der Einführung zu lösen. Ich erinnere an den Zustand.

Lassen Sie die Farbe auf rgb (120, 80, 100) eingestellt sein .
1) Was sind die Werte von RGB hat eine Farbe, die 2-mal dunkler als die angegebene ist?
2) Was sind die RGB-Werte für Grau bei gleicher Helligkeit?

Lösung:

Antworten: 1) rgb (86,56,71) ; 2) rgb (92,92,92) .

Farbtemperatur

Die in Kelvin gemessene Farbtemperatur der Lichtquelle wird durch die Temperatur des schwarzen Körpers bestimmt, der sich auf der Farbkarte an derselben Stelle befindet wie die betreffende Strahlungsquelle. Fällt die Lichtquelle nicht auf die Planck-Kurve (eine Kurve, die durch die Menge der Farbpunkte eines Schwarzkörpers bei unterschiedlichen Temperaturen bestimmt wird), wird eine korrelierte Farbtemperatur verwendet, um sie zu charakterisieren. Dieser Wert wird auch in Kelvin gemessen, bestimmt durch die Temperatur eines Schwarzkörpers, dessen Farbe der Farbe der Lichtquelle möglichst nahe kommt. Um die korrelierte Farbtemperatur der Strahlungsquelle auf der in (u, v) -Koordinaten konstruierten Farbkarte zu finden, wird der Punkt bestimmt, der der Quelle auf der Planck-Kurve am nächsten liegt (dh der kürzeste geometrische Abstand). Die Temperatur eines an dieser Stelle befindlichen Schwarzkörpers entspricht der korrelierten Farbtemperatur der betrachteten Quelle [ 4 ].

Für einen schwarzen Körper der Temperatur T wird die Strahlungsleistung pro Flächeneinheit der strahlenden Oberfläche in einem Wellenlängeneinheitsintervall durch das Plancksche Gesetz ausgedrückt:

$$

$$R (\ lambda, T) = \ frac {2 \ pi h c ^ 2} {\ lambda ^ 5} \ frac {1} {e ^ {h c / \ lambda k T} -1}$$

Dementsprechend berechne ich die spektrale Dichte der Schwarzkörperstrahlung wie folgt (in der Nullspalte der cmf2-Farbanpassungsfunktionstabelle sind die Wellenlängenwerte in Nanometern angegeben):



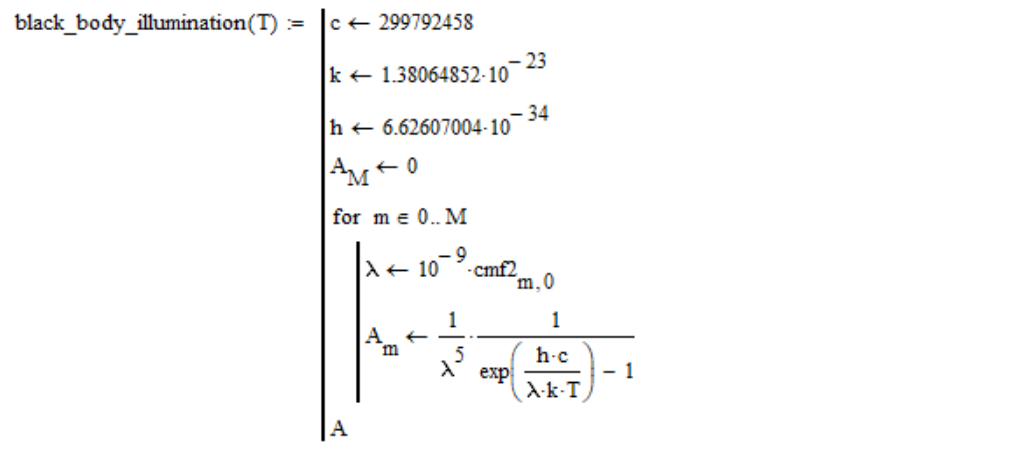
Bitte beachten Sie, dass ich den konstanten Faktor übersprungen habe, da er bei weiterer Normalisierung der Helligkeit immer noch verringert wird (die Helligkeit der Lichtquelle hat keinen Einfluss auf die Farbtemperatur).

Dann berechne ich die linearen Koordinaten von RGB:



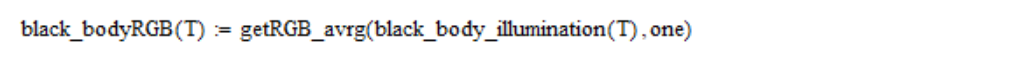
RGB-Linearkoordinaten werden wie folgt in (u, v) -Koordinaten konvertiert:



Auf der Ebene (u, v) wird der geometrische Abstand zwischen den Punkten der betrachteten Farbe und der Farbe eines schwarzen Körpers einer gegebenen Temperatur T berechnet:



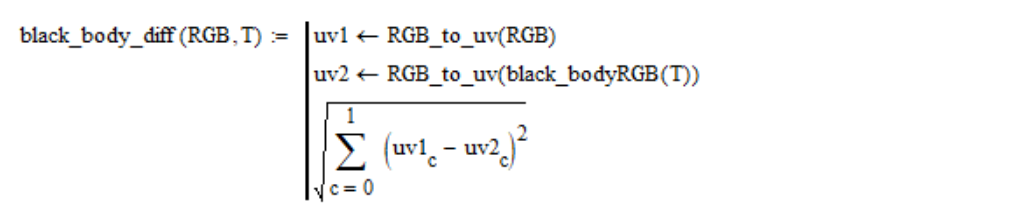
Für die Standard-Weißlichtquelle sieht die Abhängigkeit dieses Abstands von der Temperatur beispielsweise folgendermaßen aus:



Der Wert von T, bei dem diese Abhängigkeit ein Minimum aufweist, ist die Farbtemperatur der betrachteten Lichtquelle.

Die spektrale Strahlungsdichte der Sonne

Die Daten zur spektralen Dichte der Sonnenstrahlung in Abwesenheit der Atmosphäre habe ich hier heruntergeladen: [ 5 ]. Die Lichtquelle, die der Sonne aus dem All entspricht, werde ich in Zukunft als E490 bezeichnen. Auch für den Vergleich in den Berechnungen berücksichtige ich das Standardleuchtmittel D65 . Diese Quelle repräsentiert weißes Licht. Ich schaue es mir an, um zu zeigen, wie der Mond aussehen würde, wenn die Sonne weiß wäre. Die Daten der spektralen Strahlungsdichte des Standardleuchtmittels D65 habe ich hier heruntergeladen: [ 6 ].

Wie nachstehend gezeigt wird, haben die Lichtquellen D65 und E490 Farbtemperaturen von 6467 K bzw. 5912 K. Die spektralen Strahlungsdichten der Lichtquellen D65, E490 und der absolut schwarzen Körper der entsprechenden Temperaturen sind wie folgt:



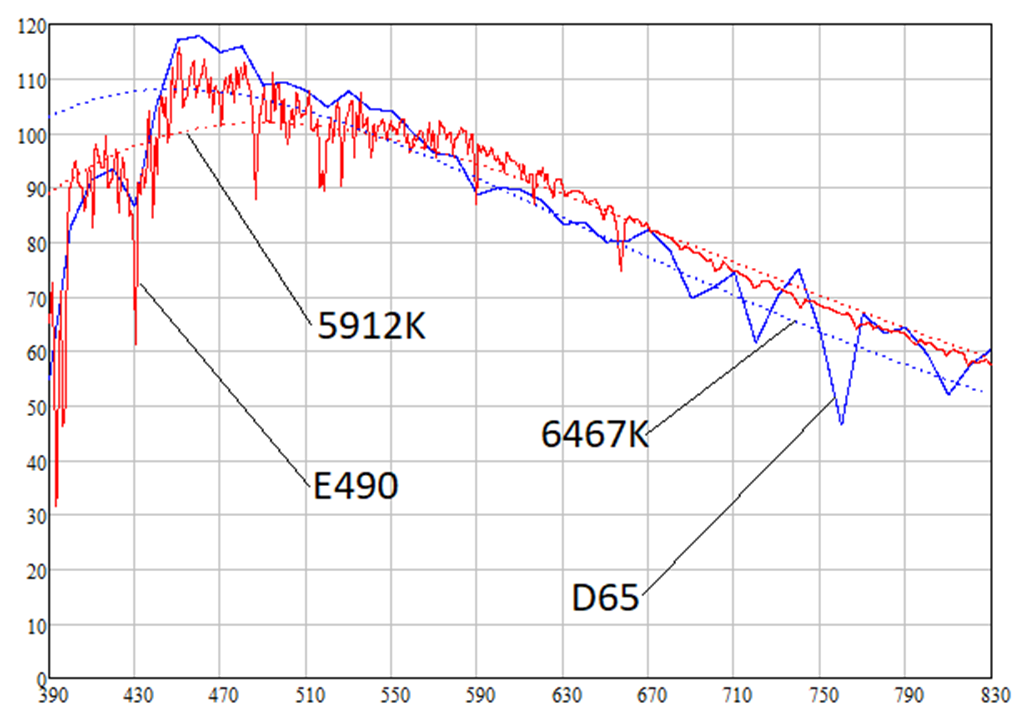
Sie sehen, dass die spektrale Dichte der Sonnenstrahlung bei längeren Wellenlängen, dh bei Wellenlängen des roten Lichts (620-770 nm), höher ist als die einer weißen Lichtquelle. Dies bedeutet, dass die Sonne einen rötlichen Farbton hat. In der Tat ergeben die Berechnungen die folgenden Farben der Lichtquellen D65, E490 und Schwarzkörper mit entsprechenden Temperaturen (wie gesagt, Weißbuch mit einer Albedo von 0,91 wird berücksichtigt):



Beachten Sie, dass die Koordinaten des sRGB der Sonne und eine Schwarzkörpertemperatur von 5912K genau übereinstimmen. Dies wird durch nichts erklärt, es passiert einfach.

Die Farbe der Kreise im letzten Bild ist die wahre Farbe der Sonne aus dem All. Das menschliche Auge sieht deutlich den rötlichen Farbton der Sonne. Die Tatsache, dass die Sonne aus dem All weiß ist, ist ein großer Mythos! Es sollte beachtet werden, dass aus irgendeinem Grund dieser Farbton auf den Apollo-Fotos und -Videos nicht beobachtet wird. In realen Fotografien würde der sichtbare rötliche Farbton der Sonne sicherlich auf den weißen Oberflächen der amerikanischen Flagge und der Raumanzüge erscheinen. Und wie weiter unten gezeigt wird, trägt dieser Farbton der Sonne wesentlich zur "Rötung" des Mondes aus dem All bei.

Ist der Mond anders oder die gleiche Farbe?

Gegner der Theorie der Mondverschwörung machen deutlich, dass der Mond eine andere Farbe hat. Angeblich ist der Mond stellenweise grau, stellenweise braun, und der Apollos ist dort gelandet, wo der Mond grau ist. Diese Version steht jedoch in direktem Widerspruch zu wissenschaftlichen Daten. In dem Artikel [ 7 ] heißt es eindeutig:

Die Farbunterschiede auf dem Mond sind extrem gering.

Shevchenko schreibt auch in seinem Buch:

Der berühmte amerikanische Forscher T. McCord hat viele Jahre in diese Richtung gearbeitet. Er erhielt mehr als 200 Spektren für verschiedene Teile der Mondoberfläche von jeweils 10 bis 20 km. Alle erhaltenen Kurven sehen grundsätzlich ähnlich aus.

Also, nein, der Mond hat keine andere Farbe, sondern die gleiche.

Farbdaten nach Shevchenko

Shevchenko gibt in seinem Buch [ 8 ] die folgende Abhängigkeit des Reflexionsvermögens von der Wellenlänge an.



Bei meinen Berechnungen wende ich die stückweise lineare Interpolation dieser Daten an. Die fehlenden Daten zum Intervall von 820-830 nm erhielt ich durch direkte Fortsetzung des Segments im Intervall von 690-820 nm.

Farbdaten nach LRO

Die Abhängigkeit des Reflexionsvermögens der Mondoberfläche von den Beleuchtungs- und Beobachtungsbedingungen bei Wellenlängen von 321 nm bis 689 nm ist in [ 9 ] angegeben. Die Modellparameter wurden basierend auf der Analyse der vom Lunar Reconnaissance Orbiter (LRO) erhaltenen Daten berechnet. Die Beleuchtungs- und Beobachtungsbedingungen werden durch die drei Parameter i (Einfallswinkel), e (Reflexionswinkel) und g (Phasenwinkel) bestimmt. Diese Winkel sind in der folgenden Abbildung dargestellt:



Der Phasenwinkel kann als Azimutwinkel ausgedrückt werden $$$\ varPsi$ unter Verwendung des sphärischen Kosinussatzes wie folgt:

$$

$$g = \ arccos \ left (\ cos \ left (i \ right) \ cos \ left (e \ right) + \ sin \ left (i \ right) \ sin \ left (e \ right) \ cos \ left ( \ varPsi \ right) \ right)$$

In den Berechnungen nehme ich die traditionellen Werte der Winkel i = g = 30 °, e = 0 °. Für solche Winkel ergibt sich folgende Abhängigkeit des Reflexionsvermögens von der Wellenlänge (Grafik Iro30):


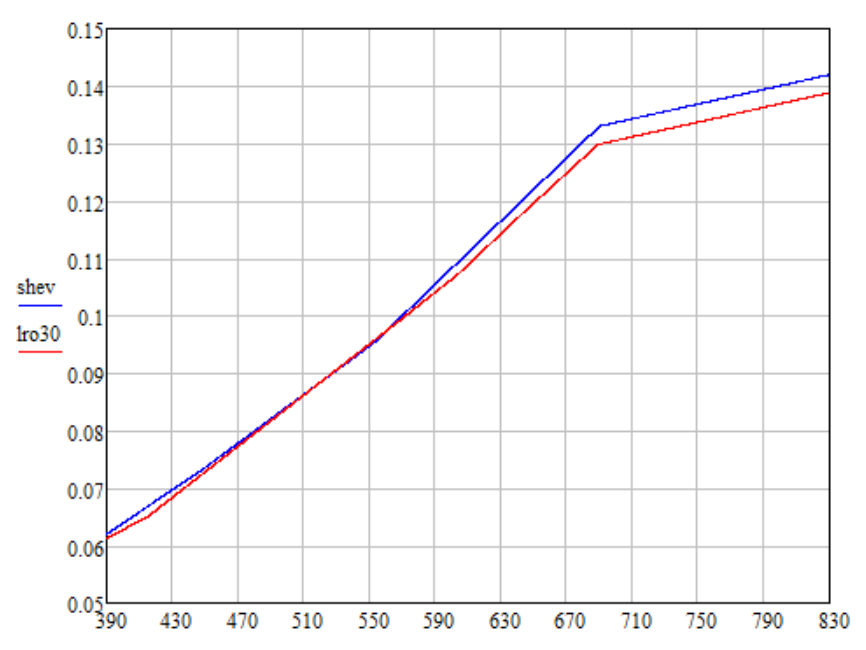
Ich habe eine lineare Extrapolation der LRO-Daten über das Intervall von 689-830 nm durchgeführt, so dass das Verhältnis der Werte an den Punkten von 830 nm und 689 nm dasselbe war wie das der Shevchenko-Daten (Shev-Plot). Ich habe auch Shevchenkos Daten durch Multiplikation mit 0,8315 renormiert, sodass die Helligkeit der resultierenden Farbe nach Shevchenko und LRO gleich war.

Farbdaten nach "Kaguya"

In [ 10 ] werden Daten des zweiten japanischen künstlichen Mond-Satelliten vorgestellt. Leider ist das Reflexionsvermögen im sichtbaren Wellenlängenbereich mit sehr geringer Auflösung angegeben, so dass ich es bei meinen Berechnungen nicht verwende.

Die Arbeit ist jedoch insofern interessant, als sie von den kolossalen Diskrepanzen zwischen den Daten von Kaguya und den Daten der Apollo 16-Mission spricht. Und dies ist einer der seltenen Fälle, in denen die wissenschaftliche Gemeinschaft offen von Inkonsistenzen spricht, die mit den Flügen der Amerikaner zum Mond verbunden sind.

Berechnungsergebnisse

Weiterhin werde ich folgende Notation verwenden:
D65 - Standard-Weißlichtquelle D65;
E490 - die Lichtquelle der Sonne in Abwesenheit der Atmosphäre;
W-0.91 - weißes Papier mit Albedo 0.91;
LRO (30 °) - LRO-Daten für herkömmliche Winkel i = g = 30 °, e = 0 °;
Shevch. - Daten von Shevchenko;
lin. (2 °) - lineare Koordinaten von RGB mit 2-Grad- Sichtfeld;
lin. (10 °) - lineare Koordinaten von RGB mit einem Sichtfeld von 10 Grad ;
lin. (Durchschnitt) - lineare Koordinaten RGB, gemittelt über das Sichtfeld von 2 Grad und 10 Grad ;
sRGB (100%) - Koordinaten von sRGB, ermittelt aus den linearen Koordinaten RGB, gemittelt über das Sichtfeld von 2 Grad und 10 Grad ;
sRGB (200%) - Koordinaten von sRGB, erhalten aus den doppelten linearen Koordinaten von RGB, gemittelt über das 2-Grad- und 10-Grad- Sichtfeld;
sRGB (300%) - Koordinaten von sRGB, erhalten aus den dreifachen linearen Koordinaten von RGB, gemittelt über das 2-Grad- und 10-Grad- Sichtfeld;
sRGB (400%) - Koordinaten von sRGB, erhalten aus den vierfachen linearen Koordinaten von RGB, gemittelt über das 2-Grad- und 10-Grad- Sichtfeld;
cl. temp. - Farbtemperatur aus den linearen Koordinaten von RGB, gemittelt über das Sichtfeld von 2 Grad und 10 Grad ;

D65

	W-0,91	LRO (30 °)	Shevch.
lin. (2 °)	0.9076,0.9120,0.8968	0,1177,0,0931,0,0688	0,1202,0,0931,0,0697
lin. (10 °)	0.9084,0.9122,0.8929	0.1165.0.0916.0.0687	0,1188,0,0917,0,0696
lin. (Durchschnitt)	0.9080,0.9121,0.8948	0,1171,0,0924,0,0688	0,1195,0,0924,0,0697
sRGB (100%)	RGB (244.245.243)	RGB (96,86,74)	RGB (97,86,75)
sRGB (200%)	-	rgb (133,119,104)	RGB (134.119.104)
sRGB (300%)	-	RGB (160, 144, 125)	RGB (161.144.126)
sRGB (400%)	-	RGB (182.164.143)	RGB (184.164.144)
cl. temp.	6467K	4928K	4891K

E490

	W-0,91	LRO (30 °)	Shevch.
lin. (2 °)	1.0005,0.8892,0.8490	0.1283.0.0909.0.0649	0,1310,0,0909,0,0657
lin. (10 °)	1.0021,0.8888,0.8483	0.1272.0.0895.0.0650	0.1297.0.0895.0.0659
lin. (Durchschnitt)	1.0013,0.8890,0.8486	0,1277,0,0902,0.0649	0,1303,0,0902,0,0658
sRGB (100%)	RGB (255.242.237)	RGB (100,85,72)	RGB (101,85,73)
sRGB (200%)	-	rgb (138,118,101)	RGB (140, 118, 102)
sRGB (300%)	-	RGB (166,142,122)	RGB (168.142.123)
sRGB (400%)	-	RGB (189.162.139)	RGB (191.162.140)
cl. temp.	5912K	4550K	4512K

Das folgende Bild zeigt die Oberflächenfarben des Mondes sRGB (100%) , sRGB (200%) (doppelte Helligkeit), sRGB (300%) (dreifache Helligkeit), sRGB (400%) (vierfache Helligkeit) mit E490- Lichtquelle (dh wenn vom Weltraum aus beobachtet) nach LRO und Shevchenko.



Wie Sie sehen können, hat der Mond aus dem Weltraum eine braune Farbe, sowohl nach LRO-Daten als auch nach Shevchenkos Daten. Shevchenko erweist sich als etwas (kaum merklich) rötlicher als LRO.

Farbe des Mondes auf den Fotos

In diesem Abschnitt werden wir die Färbung von Fotos tun. Geben Sie das Bild img und die Farbe in linearen Koordinaten RGB an. Jedes Pixel des Bildes wird durch ein Pixel einer bestimmten Farbe mit der gleichen Helligkeit wie die des Quellpixels ersetzt. Das Bild im Mathcad-Programm wird als einzelne sRGB-Koordinatenmatrix dargestellt, die durch Zusammenfügen von drei Matrizen „R“, „G“ und „B“ von links nach rechts erhalten wird. In diesem Sinne ist das Färbeverfahren wie folgt:

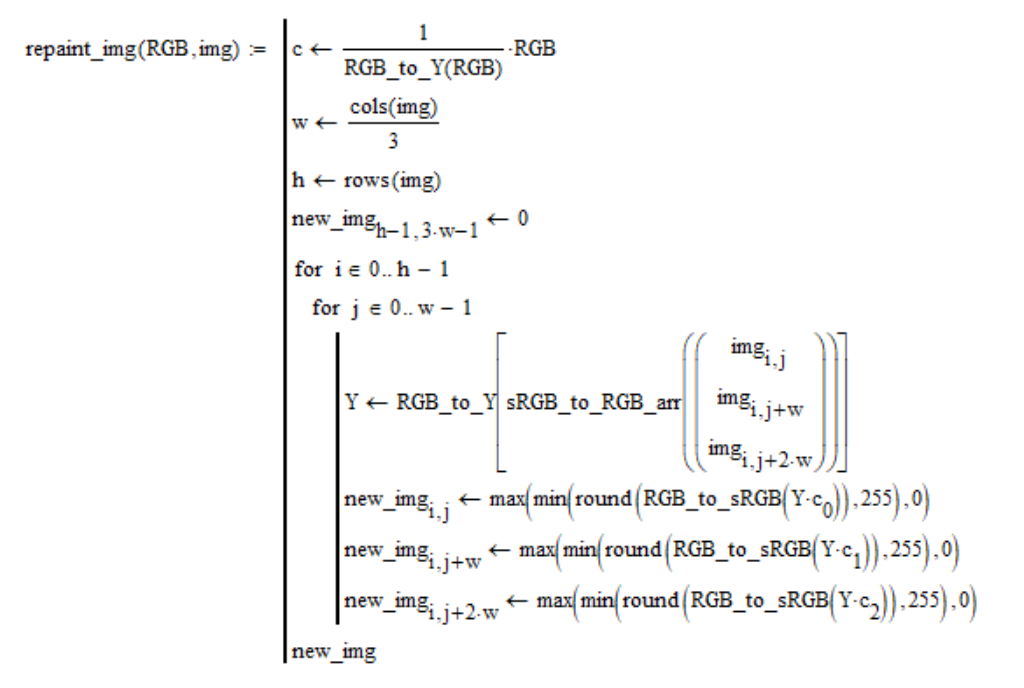
Aus Interesse habe ich das Apollo-Fotoalbum fotografiert, das die Mondoberfläche des amerikanischen Programms zeigt, und es in den Farben neu gestrichen, die ich aus meinen Berechnungen erhalten habe. Ich gebe nur die Ergebnisse und die Schlussfolgerung, dass diese authentischen Fotos oder Fälschungen selbst gemacht werden.

Das Ergebnis der Färbung des Bildes AS11-44-6552 :



In der Mitte befinden sich die Originalfotos. Links sind die Fotografien nach LRO-Angaben in traditionellen Winkeln i = g = 30 °, e = 0 ° und rechts nach Shevchenkos Angaben farbig bemalt. Die obere Reihe entspricht dem Standardleuchtmittel D65, d. H. Die obere Reihe zeigt die Farben der Mondoberfläche, die erhalten worden wären, wenn die Sonne weiß gewesen wäre. Die untere Reihe entspricht der Lichtquelle E490, d. H. Die untere Reihe zeigt die natürlichen Farben der Mondoberfläche vom Weltraum aus gesehen.

Wie Sie sehen, trägt der rötliche Farbton der Sonne wesentlich zur "Rötung" der Mondoberfläche bei, die letztendlich braun und überhaupt nicht grau aussieht.

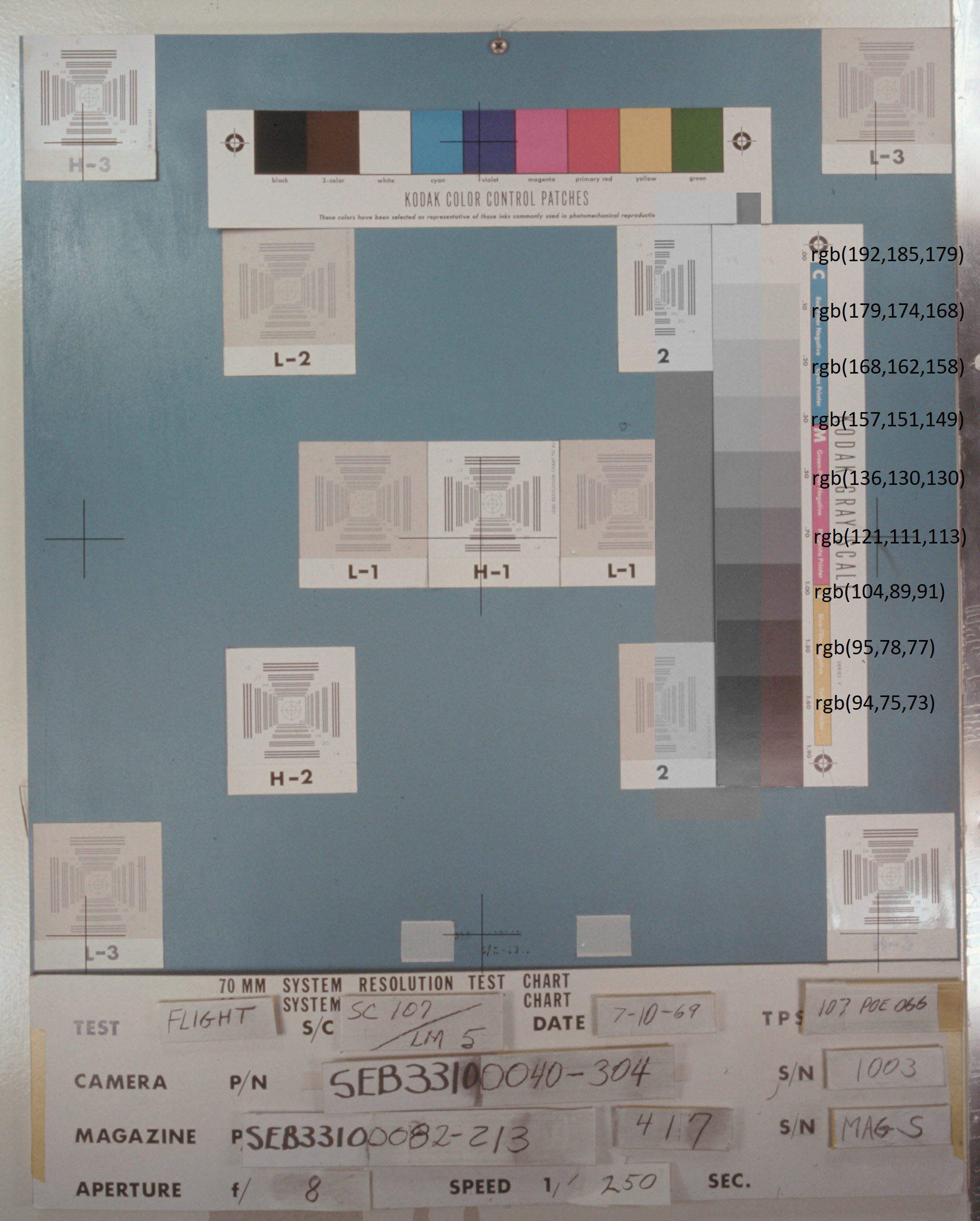
Die graue Farbe des Mondes auf den Fotos der NASA könnte durch die Tatsache erklärt werden, dass der Film aus irgendeinem Grund in Blau „verschwunden“ ist. Diese Version verschwindet jedoch sofort, wenn wir die Bilder von Graustufen am Ende der Alben analysieren. Das Foto als 11-44-Diagramm zeigt einen solchen Schnappschuss für das letzte Foto oben. Ich habe echte Grautöne mit der gleichen Helligkeit wie auf dem Foto links von den Graustufen platziert und auch die sRGB-Koordinatenwerte ausgeschrieben. Das Ergebnis war das folgende Bild:



Wie Sie sehen, ist der Film nicht nur in Blau "weggegangen", sondern sogar ein wenig in der entgegengesetzten Richtung von Blau "weggegangen". Eine solche Abweichung kann nicht braun bis grau werden.

Das Ergebnis des Ausmalbildes AS11-40-5903 :



Auf dem Originalfoto hat die Mondoberfläche stellenweise nicht nur eine graue Farbe, sondern sogar eine leichte bläuliche Tönung. Das Foto als 11-40-Diagramm zeigt das entsprechende Bild der Graustufen:



Der Film "ging weg" nicht in die "blaue" Farbe, sondern in die "rote". Und selbst danach ist die Mondoberfläche auf dem NASA-Foto aus irgendeinem Grund grau.

Das Ergebnis des Ausmalbildes AS11-37-5455 :



Dies ist eines der seltenen Fotos der Sendung "Apollo", bei der die Mondoberfläche eine, wenn auch nicht vollständige, Brauntönung aufweist. Gegner der Theorie der Mondverschwörung wollen es gerne zeigen, sagen sie, siehst braun aus. Aber der Trick hat sich hier eingeschlichen. Analysieren wir das Foto als 11-37-Diagramm , das das entsprechende Bild der Graustufen zeigt:



Der Film ist nur in braun "abgereist". Das ist der ganze Grund für die braune Färbung der Mondoberfläche in NASA-Fotografien.

Die Abhängigkeit der Farbe der Mondoberfläche von den Beleuchtungs- und Beobachtungsbedingungen

Anhand der in [ 9 ] angegebenen LRO-Daten untersuchen wir, wie sich die Farbe der Mondoberfläche von den Beleuchtungs- und Beobachtungsbedingungen unterscheidet. Betrachten Sie die Lichtquelle E490 (die Sonne aus dem Weltraum) und unterschiedliche Werte der Winkel i , e , $$$\ varPsi$ . Das folgende Bild zeigt das Ergebnis, wobei in der oberen Reihe Farben mit dreifacher Helligkeit und in der unteren Reihe Farben mit gleicher Helligkeit Y = 0,5 dargestellt sind .



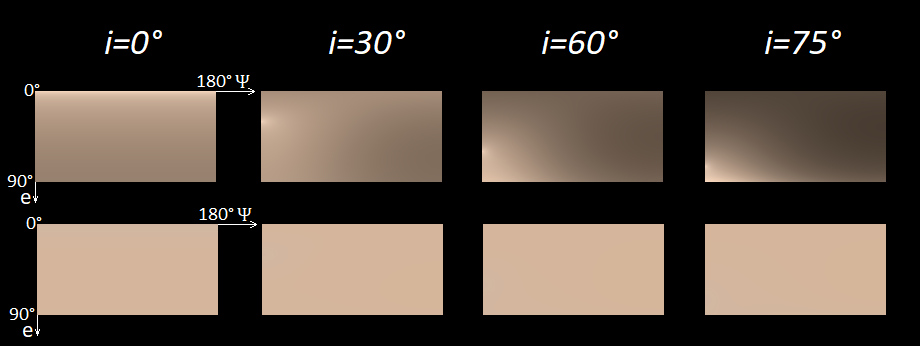
Wie aus dem Bild ersichtlich, ändert sich nur die Helligkeit. In der unteren Reihe sind die Farben für das menschliche Auge fast überall gleich. Wenn Sie genau hinschauen, können Sie im Fall von i = 0 ° eine sehr geringe Abweichung in der Graurichtung sehen, wenn sich e Null nähert.

Mondbodenfarbe

Die NASA-Website hat ein sehr seltsames Foto, nämlich dieses Foto der Mondbodenprobe Nr. 10005 .



Der Mondboden auf dem Foto sieht braun aus, sogar zu braun, da das Licht von einer weißen Lichtquelle erzeugt wurde. Die Richtigkeit des Weißabgleichs kann anhand der Farbe des im Rahmen enthaltenen Weißbuchs überprüft werden.

Vielleicht ist dies derselbe orangefarbene Grund, den die Apollo 17-Astronauten gefunden haben? Nicht! Aus dem Dokument [ 11 ] geht eindeutig hervor, dass die Probe von den Apollo 11-Astronauten entnommen wurde.

Und jetzt hören wir uns an, was Neil Armstrong (Apollo 11-Astronaut) in einem Interview mit Patrick Moore [ 12 ] aus dem Jahr 1970 sagt.

Wenn Sie das Material aus nächster Nähe betrachten, als ob Sie es in der Hand hätten, stellen Sie fest, dass es in der Tat anthrazitgrau ist, und wir konnten nie Dinge finden, die sich von dieser Farbe sehr unterschieden.

Es stellte sich heraus, dass Neil Armstrong, der keine Angst vor dem Wort hatte, gelogen hatte.

Literatur

1. Color & Vision Research Laboratory - Neue CIE XYZ-Funktionen, die aus den CIE (2006) LMS-Funktionen abgeleitet wurden
2. Internationales Farbkonsortium - Ein Standardfarbraum für das Internet: sRGB
3. Empfehlung ITU-RBT.709 - Parameterwerte für die HDTV-Standards für Produktion und internationalen Programmaustausch
4. Robertson R. “Berechnung der korrelierten Farbtemperatur und Verteilungstemperatur” /.Opt. Soc. Am. 58, 1528 (1968).
5. 2000 ASTM Standard Extraterrestrial Spectrum Reference E-490-00
6. CIE-Normlichtart D65
7. "Die ersten Ergebnisse der Bestimmung der physikomechanischen Eigenschaften der Böden des Mondes", M .: 1970. Gosstroy der UdSSR, hrsg. prof. Dr. Techn. Wissenschaften VG Bulycheva, p. 8. ("Die ersten Ergebnisse der Bestimmung der physikalisch-mechanischen Eigenschaften der Böden des Mondes", Moskau: 1970. Gosstroy, UdSSR, unter der Leitung von Prof. Dr. Sc. VG Bulychev, S. 8.)
8. Shevchenko VV, Der Mond und seine Beobachtung, 1983, pp. 91-92. (Shevchenko V.V., Moon und seine Beobachtung, 1983, S. 91-92.)
9. B. Hapke, B. Denevi, H. Sato, S. Braden und M. Robinson (2012), Die Wellenlängenabhängigkeit der Mondphasenkurve aus Sicht der Weitwinkelkamera Lunar Reconnaissance Orbiter, J. Geophys. Res., 117, E00H15
10. Ohtake, M. et al. (2010), Ableiten des absoluten Reflexionsvermögens der Mondoberfläche unter Verwendung von SELENE (Kaguya) Multiband Imager-Daten, Space Sci. Rev., 154, 57 & ndash; 77
11. THE APOLLO 11 DRIVE TUBES, Dissektion und Beschreibung von Judith H. Allton, NASA (1978)
12. BBC Neil Armstrong spricht mit Patrick Moore (1970)