Wie man ein neuronales Netzwerk lehrt, um die Spielphysik zu reproduzieren

In fast jedem modernen Computerspiel ist das Vorhandensein einer physischen Engine eine Grundvoraussetzung. Im Wind flatternde Fahnen und Hasen, die von Kugeln bombardiert werden - all dies erfordert eine ordnungsgemäße Ausführung. Und natürlich, auch wenn nicht alle Helden Regenmäntel tragen ... aber diejenigen, die das tragen, brauchen wirklich eine angemessene Simulation von flatterndem Stoff.



Eine vollständige physikalische Modellierung solcher Wechselwirkungen wird jedoch häufig unmöglich, da sie um Größenordnungen langsamer ist als für Echtzeitspiele erforderlich. Dieser Artikel bietet eine neue Modellierungsmethode, mit der physikalische Simulationen um das 300- bis 5000-fache beschleunigt werden können. Ziel ist es, ein neuronales Netzwerk zu unterrichten, um physikalische Kräfte zu simulieren.

Fortschritte bei der Entwicklung physikalischer Motoren werden sowohl von der wachsenden Rechenleistung technischer Geräte als auch von der Entwicklung schneller und stabiler Modellierungsmethoden bestimmt. Zu diesen Methoden gehört beispielsweise die Modellierung durch Aufteilung des Raums in Teilräume und datengesteuerte Ansätze - das heißt, basierend auf Daten. Erstere arbeiten nur in einem reduzierten oder komprimierten Unterraum, in dem nur wenige Verformungsformen berücksichtigt werden. Dies kann bei großen Projekten zu einem deutlichen Anstieg der technischen Anforderungen führen. Datengesteuerte Ansätze verwenden den Systemspeicher und die darin gespeicherten vorberechneten Daten, wodurch diese Anforderungen reduziert werden.

Hier betrachten wir einen Ansatz, der beide Methoden kombiniert: Auf diese Weise sollen die Stärken beider genutzt werden. Eine solche Methode kann auf zwei Arten interpretiert werden: entweder als Subraummodellierungsmethode, die von einem neuronalen Netzwerk parametrisiert wird, oder als DD-Methode, die auf Subraummodellierung basiert, um ein komprimiertes simuliertes Medium zu erstellen.

Das Wesentliche dabei ist: Zuerst sammeln wir mit Maya nCloth hochpräzise Simulationsdaten und berechnen dann den linearen Unterraum mit der Hauptkomponentenmethode (PCA) . Im nächsten Schritt verwenden wir maschinelles Lernen auf der Grundlage des klassischen neuronalen Netzwerkmodells und unserer neuen Methodik. Anschließend führen wir das trainierte Modell in einen interaktiven Algorithmus mit mehreren Optimierungen ein, z. B. einen effizienten Dekomprimierungsalgorithmus durch eine GPU und eine Methode zur Approximation von Vertexnormalen.


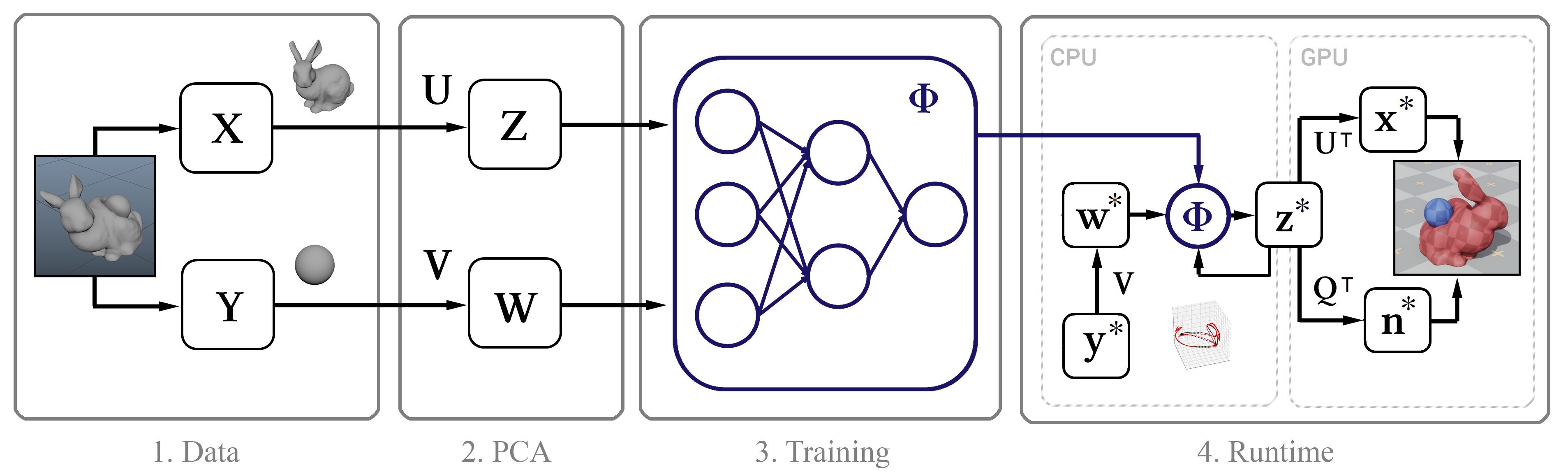Abbildung 1. Das Strukturdiagramm der Methode

Trainingsdaten

Im Allgemeinen ist die einzige Eingabe für diese Methode der rohe Zeitstempel der rahmenweisen Positionen der Scheitelpunkte des Objekts. Als nächstes beschreiben wir den Prozess der Erfassung solcher Daten.

Wir führen die Simulation in Maya nCloth durch und erfassen Daten mit einer Geschwindigkeit von 60 Bildern pro Sekunde. Je nach Stabilität der Simulation werden 5 oder 20 Unterschritte und 10 oder 25 begrenzende Iterationen ausgeführt. Nehmen Sie für Stoffe ein T-Shirt-Modell mit einer leichten Gewichtszunahme des Materials und seiner Beständigkeit gegen Dehnung und für verformbare Objekte Hartgummi mit verringerter Reibung. Wir führen externe Kollisionen durch, indem wir Dreiecke mit externer Geometrie kollidieren, Selbstkollisionen - Scheitelpunkte mit Scheitelpunkten für Stoff und Dreiecke mit Dreiecken für Gummi. In allen Fällen verwenden wir eine ziemlich große Dicke der Kollision - in der Größenordnung von 5 cm -, um die Stabilität des Modells zu gewährleisten und ein Einklemmen und Reißen des Gewebes zu verhindern.

Tabelle 1. Parameter der modellierten Objekte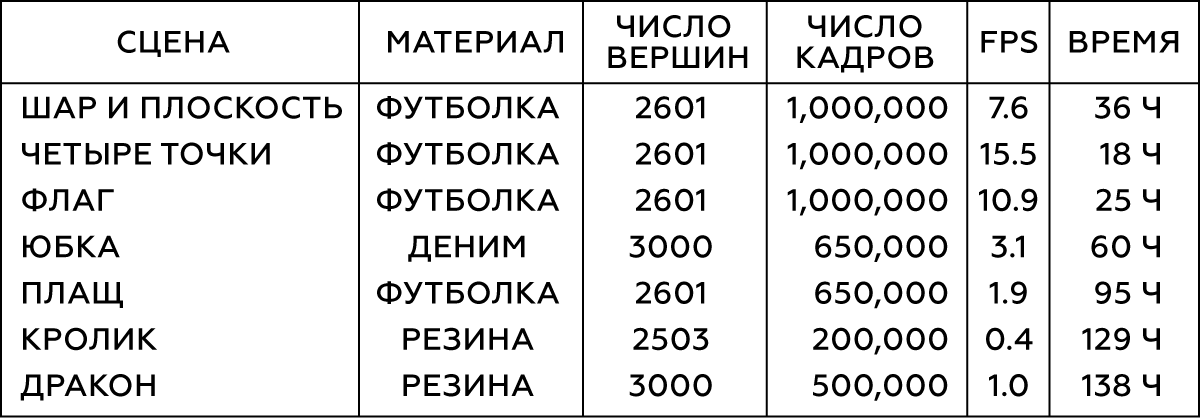


Für verschiedene Arten der Interaktion einfacher Objekte (z. B. Kugeln) erzeugen wir ihre Bewegung auf zufällige Weise, indem wir zufällige Koordinaten zu zufälligen Zeiten beschneiden. Um die Interaktion von Gewebe mit einem Charakter zu simulieren, verwenden wir eine Motion-Capture-Datenbank mit 6,5 × 10 ⁵ Bildern, die eine große Animation darstellen. Nach Abschluss der Simulation überprüfen wir das Ergebnis und schließen Frames mit instabilem oder schlechtem Verhalten aus. Für die Szene mit dem Rock entfernen wir die Hände des Charakters, da sie sich häufig mit der Geometrie des Beingeflechts schneiden und jetzt unbedeutend sind.


Abbildung 2. Die ersten beiden Szenen aus der Tabelle

Normalerweise benötigen wir 10 ⁵ -10 ⁶ Frames mit Trainingsdaten. Nach unserer Erfahrung reichen in den meisten Fällen 10 ⁵ Frames zum Testen aus, während die besten Ergebnisse mit 10 ⁶ Frames erzielt werden.

Schulung

Als nächstes werden wir über den Prozess des maschinellen Lernens sprechen: über die Parametrisierung in unserem neuronalen Netzwerk, über die Netzwerkarchitektur und direkt über die Technik selbst.

Parametrierung

Um einen Trainingsdatensatz zu erhalten, sammeln wir die Koordinaten der Eckpunkte in jedem Rahmen t zu einem Vektor x _t und kombinieren diese rahmenweisen Vektoren dann zu einer großen Matrix X. Diese Matrix beschreibt die Zustände des modellierten Objekts. Außerdem müssen wir eine Vorstellung vom Zustand der externen Objekte in jedem Frame haben. Für einfache Objekte (z. B. Bälle) können Sie ihre dreidimensionalen Koordinaten verwenden, während der Zustand komplexer Modelle (Zeichen) durch die Position jedes Gelenks relativ zum Referenzpunkt beschrieben wird: Bei einem Rock ist eine solche Stütze das Hüftgelenk, bei einem Mantel der Hals. Bei Objekten mit einem sich bewegenden Bezugssystem sollte die Position der Erde relativ dazu berücksichtigt werden: Dann kennt unser System die Richtung der Schwerkraft sowie deren lineare Geschwindigkeit, Beschleunigung, Rotationsgeschwindigkeit und Rotationsbeschleunigung. Bei der Flagge berücksichtigen wir die Geschwindigkeit und Richtung des Windes. Als Ergebnis erhalten wir für jedes Objekt einen großen Vektor, der den Zustand des externen Objekts beschreibt, und alle diese Vektoren werden auch in der Matrix Y kombiniert.

Nun wenden wir die PCA sowohl auf die Matrix X als auch auf die Matrix Y an und verwenden die resultierenden Transformationsmatrizen Z und W, um das Unterraumbild zu konstruieren. Wenn die PCA-Prozedur zu viel Speicher benötigt, probieren Sie zuerst unsere Daten aus.

Die PCA-Komprimierung führt unweigerlich zu Detailverlusten, insbesondere bei Objekten mit vielen potenziellen Bedingungen, wie z. B. dünnen Stofffalten. Wenn der Unterraum jedoch aus 256 Basisvektoren besteht, hilft dies normalerweise, die meisten Details zu erhalten. Im Folgenden finden Sie Animationen der Standardphysik des Mantels und der Modelle mit 256, 128 bzw. 64 Basisvektoren.


Abbildung 3. Vergleich des Kontrollmodells (Standard) mit den Modellen unserer Methode in Räumen mit unterschiedlichen Bemaßungsgrundlagen

Quelle und erweitertes Modell

Es war notwendig, ein Modell zu entwickeln, das den Zustand von Modellvektoren in zukünftigen Frames vorhersagen kann. Und da die modellierten Objekte normalerweise durch Trägheit mit einer Tendenz zu einem bestimmten mittleren Ruhezustand gekennzeichnet sind (nach dem PCA-Verfahren nimmt das Objekt einen solchen Zustand bei Nullwerten an), wäre ein gutes Anfangsmodell der Ausdruck, der durch die Linie 9 des Algorithmus in 4 dargestellt wird. Hier sind α und β die Modellparameter, ⊙ ist ein explodiertes Produkt. Die Werte dieser Parameter werden aus den Quellendaten erhalten, indem die lineare Gleichung der kleinsten Quadrate individuell für α und β gelöst wird:



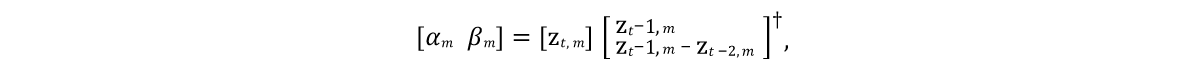
Hier ist † die pseudoinverse Transformation der Matrix .

Da eine solche Vorhersage nur eine sehr grobe Annäherung ist und den Einfluss externer Objekte w nicht berücksichtigt, ist sie offensichtlich nicht in der Lage, die Trainingsdaten genau zu modellieren. Daher trainieren wir das neuronale Netz Φ, um die Resteffekte des Modells gemäß der 11. Zeile des Algorithmus zu approximieren. Hier parametrisieren wir mit der Aktivierungsfunktion ReLU ein standardmäßiges direktverteilendes neuronales Netzwerk mit 10 Schichten für jede Schicht (mit Ausnahme der Ausgabe). Mit Ausnahme der Eingabe- und Ausgabeebene setzen wir die Anzahl der ausgeblendeten Einheiten auf jeder verbleibenden Ebene auf eineinhalb der Größe der PCA-Daten, was zu einem guten Kompromiss zwischen dem belegten Speicherplatz auf der Festplatte und der Leistung führte.


Abbildung 4. Lernalgorithmus für neuronale Netze

Neuronales Netz-Training

Eine Standardmethode zum Trainieren eines neuronalen Netzwerks besteht darin, den gesamten Datensatz zu durchlaufen und das Netzwerk zu trainieren, um Vorhersagen für jeden Frame zu treffen. Ein solcher Ansatz führt natürlich zu einem geringen Lernfehler, aber die Rückkopplung in einer solchen Vorhersage führt zu einem instabilen Verhalten des Ergebnisses. Um eine stabile Langzeitvorhersage zu gewährleisten, verwendet unser Algorithmus daher die Methode der Rückübertragung von Fehlern während des gesamten Integrationsvorgangs.

Im Allgemeinen funktioniert das so: Aus einem kleinen Fenster mit Trainingsdaten z und w nehmen wir die ersten beiden Frames z ₀ und z ₁ und fügen ihnen ein kleines Rauschen r ₀ , r _{1 hinzu} , um den Lernpfad geringfügig zu stören. Um die nächsten Frames vorherzusagen, führen wir den Algorithmus mehrmals aus und kehren bei jedem neuen Zeitschritt zu den vorherigen Ergebnissen der Vorhersagen zurück. Sobald wir eine Vorhersage der gesamten Flugbahn erhalten, berechnen wir den durchschnittlichen Koordinatenfehler und übergeben ihn dann an den AmsGrad-Optimierer unter Verwendung der mit TensorFlow berechneten automatischen Ableitungen.

Wir werden diesen Algorithmus an Mini-Samples von 16 Frames mit überlappenden Fenstern von 32 Frames für 100 Epochen oder bis zur Konvergenz des Trainings wiederholen. Wir verwenden die Lernrate von 0,0001, den Dämpfungskoeffizienten der Lernrate von 0,999 und die aus den ersten drei Komponenten des PCA-Raums berechnete Standardabweichung des Rauschens. Diese Schulung dauert je nach Komplexität der Installation und Größe der PCA-Daten 10 bis 48 Stunden.


Abbildung 5. Visueller Vergleich des Referenzrocks und desjenigen, den unser neuronales Netzwerk zu bauen gelernt hat

Systemimplementierung

Wir werden die Implementierung unserer Methode in einer interaktiven Umgebung detailliert beschreiben, einschließlich der Bewertung eines neuronalen Netzwerks, der Berechnung der Normalen zu den Oberflächen von Objekten zum Rendern und des Umgangs mit sichtbaren Schnittpunkten.

Rendering-App

Wir rendern die resultierenden Modelle in einer einfachen interaktiven 3D-Anwendung, die in C ++ und DirectX geschrieben wurde: Wir implementieren erneut die Vorprozesse und neuronalen Netzwerkoperationen in Single-Threaded-C ++ - Code und laden die binären Netzwerkgewichtungen, die während unseres Trainingsprozesses erhalten wurden. Dann wenden wir einige einfache Optimierungen für die Netzwerkschätzung an, insbesondere die Wiederverwendung von Speicherpuffern und spärlichen Vektor-Matrix-Daten, die aufgrund des Vorhandenseins von Null verborgenen Einheiten möglich werden, die dank der ReLU-Aktivierungsfunktion erhalten werden.

GPU-Dekomprimierung

Senden Sie komprimierte z-Statusdaten an die GPU und dekomprimieren Sie sie für das weitere Rendern. Zu diesem Zweck verwenden wir einen einfachen Berechnungsshader, der für jeden Scheitelpunkt des Objekts das Punktprodukt des Vektors z und der ersten drei Zeilen der Matrix U ^T berechnet, die den Koordinaten dieses Scheitelpunkts entsprechen, und anschließend den Durchschnittswert x _µ addiert. Dieser Ansatz hat zwei Vorteile gegenüber der naiven Dekomprimierungsmethode. Erstens beschleunigt die Parallelität der GPU die Berechnung des Modellzustandsvektors erheblich, was bis zu 1 ms dauern kann. Zweitens wird die Datenübertragungszeit zwischen der Zentrale und der GPU um eine Größenordnung verkürzt, was insbesondere für Plattformen wichtig ist, auf denen die Übertragung des gesamten Zustands des gesamten Objekts zu langsam ist.

Vertex-Normalvorhersage

Während des Renderns reicht es nicht aus, nur auf die Koordinaten der Scheitelpunkte zuzugreifen, sondern es werden auch Informationen über die Verformungen ihrer Normalen benötigt. In der Regel lassen Sie in einer physischen Engine diese Berechnung entweder weg oder führen eine naive Frame-für-Frame-Neuberechnung von Normalen mit anschließender Umverteilung auf benachbarte Scheitelpunkte durch. Dies kann sich als ineffizient herausstellen, da die grundlegende Implementierung des Zentralprozessors zusätzlich zu den Kosten für Dekomprimierung und Datenübertragung weitere 150 μs für ein solches Verfahren erfordert. Und obwohl diese Berechnung auf der GPU durchgeführt werden kann, gestaltet sich die Implementierung aufgrund der Notwendigkeit von Paralleloperationen schwieriger.

Stattdessen führen wir auf dem GPU-Shader eine lineare Regression des Zustands des Unterraums zu normalen Vollzustandsvektoren durch. Wenn wir die Werte der Normalen der Eckpunkte in jedem Frame kennen, berechnen wir die Matrix Q, die die Darstellung des Unterraums auf den Normalen der Eckpunkte am besten darstellt.

Da die Vorhersage von Normalen in unserer Methode noch nie zuvor vorgestellt wurde, gibt es keine Garantie dafür, dass dieser Ansatz korrekt ist, aber in der Praxis hat er sich als wirklich gut erwiesen, wie aus der folgenden Abbildung ersichtlich ist.


Abbildung 6. Vergleich der mit unserer Methode berechneten Modelle und der Referenz (Grundwahrheit) sowie der Differenz zwischen ihnen

Kreuzungskampf

Unser neuronales Netzwerk lernt, Kollisionen effizient auszuführen. Aufgrund von Ungenauigkeiten bei Vorhersagen und Fehlern, die durch die Komprimierung des Unterraums verursacht werden, können jedoch Schnittpunkte zwischen externen und simulierten Objekten auftreten. Da wir die Berechnung des vollständigen Zustands der Szene auf den Anfang des Renderns verschieben, gibt es darüber hinaus keine Möglichkeit, diese Probleme im Voraus effektiv zu lösen. Um eine hohe Leistung aufrechtzuerhalten, müssen diese Überschneidungen beim Rendern entfernt werden.

Wir haben dafür eine einfache und effektive Lösung gefunden, die darin besteht, dass sich überschneidende Scheitelpunkte auf die Oberfläche der Grundelemente projiziert werden, aus denen wir den Charakter bilden. Diese Projektion ist auf der GPU mit demselben Computer-Shader einfach durchzuführen, mit dem die Fabric dekomprimiert und die normale Schattierung berechnet wird.

Zunächst komponieren wir ein Zeichen aus Proxy-Objekten, die mit Scheitelpunkten mit unterschiedlichen Anfangs- und Endradien verbunden sind, und übertragen anschließend Informationen über die Koordinaten und Radien dieser Objekte an den Computing-Shader. Überprüfen Sie erneut die Koordinaten jedes Scheitelpunkts auf Schnittpunkte mit dem entsprechenden Proxy-Objekt und projizieren Sie diesen Scheitelpunkt, falls dies der Fall ist, auf die Oberfläche des Proxy-Objekts. Wir korrigieren also nur die Position des Scheitelpunkts, ohne die Normale selbst zu berühren, um die Schattierung nicht zu beschädigen.

Bei diesem Ansatz werden kleine sichtbare Überschneidungen von Objekten entfernt, vorausgesetzt, die Fehler der Scheitelpunktverschiebung sind nicht so groß, dass sich die Projektion auf der gegenüberliegenden Seite des entsprechenden Proxy-Objekts befindet.


Abbildung 7. Zeichenmodell bestehend aus Proxy-Objekten und den Ergebnissen der Beseitigung sichtbarer Überschneidungen mithilfe unserer Methode: Vorher und Nachher

Ergebnisermittlung

Unsere Testszenen umfassen also:

• , ;
• , , ;
• , ;
• , ;
• , ;
• , .

, .

- 16 , 120 240 .


8. 16 . Party time!

, , , , .

, PCA. , , , .


9. , , –

Ausführung

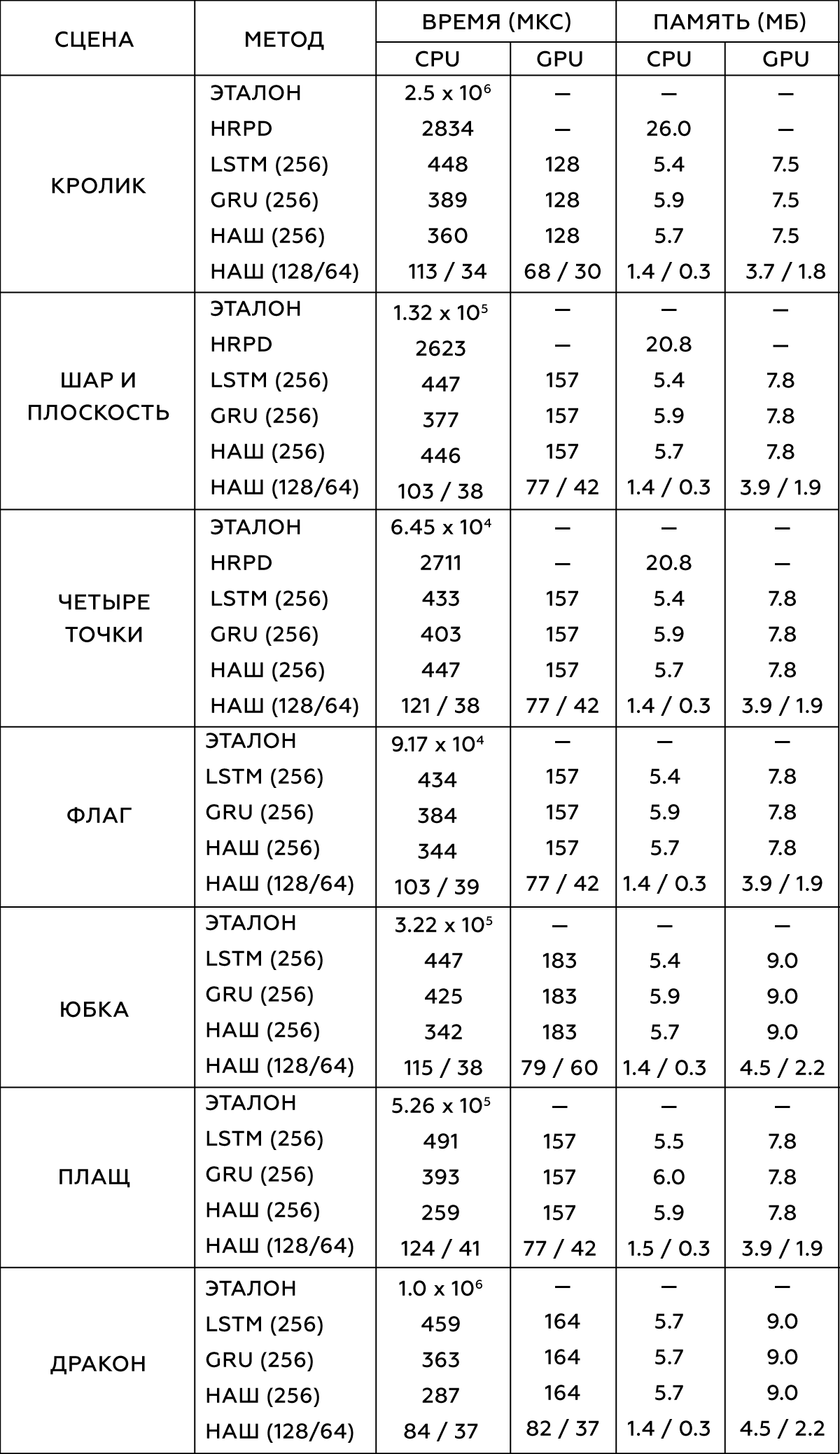
― , . , . 300-5000 , . , - (HRPD) , (LSTM) (GRU) .

, . Intel Xeon E5-1650 3.5 GHz GeForce GTX 1080 Titan.

2.

, , . , .

data-driven , . , , , , , . , , ― , .

, , , .

, . data-driven , ― , . , , , . , , , .

, . .

, , , . , , ― , . -, , , - . .

, , , , . , , , , ― , , . .

.


10. vs : choose your fighter