Wir bringen die lineare Regressionsgleichung in Matrixform

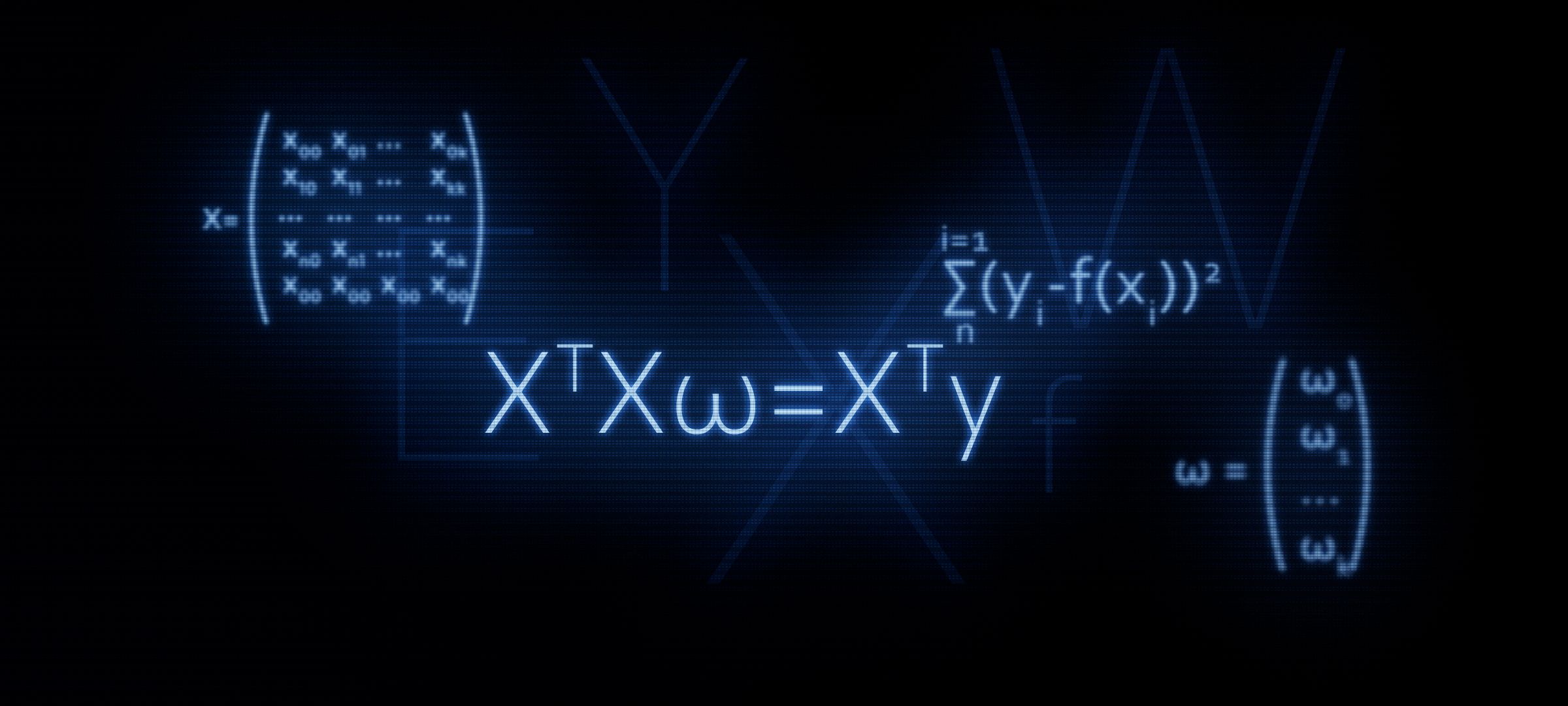
Der Zweck dieses Artikels ist es, unerfahrenen Datenschreibern Unterstützung zu bieten. Im vorherigen Artikel haben wir drei Methoden zur Lösung der linearen Regressionsgleichung an den Fingern untersucht: analytische Lösung, Gradientenabstieg, stochastischer Gradientenabstieg. Dann haben wir für die analytische Lösung die Formel angewendet $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ . In diesem Artikel werden wir, wie aus dem Titel hervorgeht, die Verwendung dieser Formel begründen, oder mit anderen Worten, wir werden sie unabhängig ableiten.

Warum es sinnvoll ist, der Formel mehr Aufmerksamkeit zu schenken $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ ?

Mit der Matrixgleichung beginnt in den meisten Fällen die Bekanntschaft mit der linearen Regression. Gleichzeitig sind detaillierte Berechnungen, wie die Formel abgeleitet wurde, selten.

In Yandex-Kursen für maschinelles Lernen empfehlen die Schüler beispielsweise, wenn sie in die Regularisierung eingeführt werden, die Funktionen aus der sklearn- Bibliothek zu verwenden, während kein Wort über die Matrixdarstellung des Algorithmus erwähnt wird. In diesem Moment möchten einige Hörer dieses Problem möglicherweise genauer verstehen - schreiben Sie Code, ohne fertige Funktionen zu verwenden. Dazu müssen wir zunächst die Gleichung mit dem Regularisierer in Matrixform darstellen. Dieser Artikel ermöglicht es denen, die solche Fähigkeiten beherrschen möchten. Fangen wir an.

Grundlinie

Ziele

Wir haben eine Reihe von Zielwerten. Das Ziel kann beispielsweise der Preis eines Vermögenswerts sein: Öl, Gold, Weizen, Dollar usw. Gleichzeitig meinen wir mit einer Anzahl von Werten des Zielindikators die Anzahl von Beobachtungen. Solche Beobachtungen können zum Beispiel die monatlichen Ölpreise für das Jahr sein, dh wir werden 12 Zielwerte haben. Wir beginnen die Notation einzuführen. Wir bezeichnen jeden Zielwert als $$$y_i$ . Insgesamt haben wir $$$n$ Beobachtungen, das heißt, wir können uns unsere Beobachtungen als vorstellen $$$y_1, y_2, y_3 ... y_n$ .

Regressoren

Wir gehen davon aus, dass es Faktoren gibt, die die Werte des Zielindikators zum Teil erklären. Zum Beispiel wird der Wechselkurs des Dollar / Rubel-Paares stark vom Ölpreis, dem Fed-Kurs usw. beeinflusst. Solche Faktoren werden als Regressoren bezeichnet. Gleichzeitig muss jeder Wert des Zielindikators dem Wert des Regressors entsprechen, dh wenn wir 2018 für jeden Monat 12 Ziele haben, müssen wir auch 12 Regressoren für denselben Zeitraum haben. Bezeichnen Sie die Werte jedes Regressors mit $$$x_i: x_1, x_2, x_3 ... x_n$ . Lassen Sie in unserem Fall gibt es $$$k$ Regressoren (d. h. $$$k$ Faktoren, die den Wert des Ziels beeinflussen). So können unsere Regressoren wie folgt dargestellt werden: für den 1. Regressor (zum Beispiel den Ölpreis): $$$x_ {11}, x_ {12}, x_ {13} ... x_ {1n}$ , für den 2. Regressor (zum Beispiel die Fed-Rate): $$$x_ {21}, x_ {22}, x_ {23} ... x_ {2n}$ für $$$k$ der "Regressor: $$$x_ {k1}, x_ {k2}, x_ {k3} ... x_ {kn}$

Abhängigkeit der Ziele von Regressoren

Zielabhängigkeit annehmen $$$y_i$ von Regressoren " $$$i$ -th "Beobachtung kann durch die lineare Regressionsgleichung der Form ausgedrückt werden:

$$

$$f (w, x_i) = w_0 + w_1 x_ {1i} + ... + w_k x_ {ki}$$

wo $$$x_i$ - " $$$i$ "Regressorwert von 1 bis $$$n$ ,

$$$k$ - die Anzahl der Regressoren von 1 bis $$$k$

$$$w$ - Winkelkoeffizienten, die den Betrag darstellen, um den sich der berechnete Zielindikator im Durchschnitt ändert, wenn sich der Regressor ändert.

Mit anderen Worten, wir sind für alle da (außer $$$w_0$ ) des Regressors bestimmen wir "unseren" Koeffizienten $$$w$ , dann multiplizieren Sie die Koeffizienten mit den Werten der Regressoren " $$$i$ -th "Beobachtung, als Ergebnis bekommen wir eine gewisse Annäherung" $$$i$ das "Ziel.

Daher müssen wir solche Koeffizienten auswählen $$$w$ für die die Werte unserer Näherungsfunktion $$$f (w, x_i)$ wird so nahe wie möglich an den Werten der Ziele liegen.

Abschätzung der Qualität der Approximationsfunktion

Wir werden die Qualitätsschätzung der Approximationsfunktion nach der Methode der kleinsten Quadrate bestimmen. Die Qualitätsbewertungsfunktion hat in diesem Fall die folgende Form:

$$

$$Err = \ sum \ limits_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ rightarrow min$$

Wir müssen solche Werte der Koeffizienten $ w $ wählen, für die der Wert gilt $$$Err$ wird der kleinste sein.

Wir übersetzen die Gleichung in Matrixform

Vektoransicht

Um Ihnen das Leben zu erleichtern, sollten Sie zunächst die lineare Regressionsgleichung und den ersten Koeffizienten beachten $$$w_0$ nicht mit einem Regressor multipliziert. Wenn wir die Daten in Matrixform übersetzen, wird der obige Umstand die Berechnungen außerdem ernsthaft erschweren. In diesem Zusammenhang wird vorgeschlagen, einen weiteren Regressor für den ersten Koeffizienten einzuführen $$$w_0$ und gleich eins. Oder vielmehr jeder " $$$i$ Der "Wert" dieses Regressors ist gleichbedeutend mit der Einheit - denn wenn er mit der Einheit multipliziert wird, ändert sich nichts im Hinblick auf das Ergebnis der Berechnungen und im Hinblick auf die Regeln für das Produkt der Matrizen, wird unsere Qual erheblich verringert.

Nehmen wir nun für eine Weile an, wir hätten nur eine, um das Material zu vereinfachen. " $$$i$ th "Beobachtung. Dann stellen Sie sich die Werte der Regressoren" $$$i$ Beobachtung als Vektor $$$\ vec {x_i}$ . Vektor $$$\ vec {x_i}$ hat Dimension $$$(k \ times 1)$ , also $$$k$ Zeilen und 1 Spalte:

$$

$$\ vec {x_i} = \ begin {pmatrix} x_ {0i} \\ x_ {1i} \\ ... \\ x_ {ki} \ end {pmatrix} \ qquad$$

Die gewünschten Koeffizienten können als Vektor dargestellt werden $$$\ vec {w}$ Dimension haben $$$(k \ times 1)$ :

$$

$$\ vec {w} = \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$$

Die lineare Regressionsgleichung für $$$i$ -th "Beobachtung wird die Form annehmen:

$$

$$f (w, x_i) = \ vec {x_i} ^ T \ vec {w}$$

Die Qualitätsbewertungsfunktion des linearen Modells hat folgende Form:

$$

$$Err = \ sum \ limits_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 \ rightarrow min$$

Beachten Sie, dass wir gemäß den Regeln der Matrixmultiplikation den Vektor transponieren mussten $$$\ vec {x_i}$ .

Matrixdarstellung

Als Ergebnis der Multiplikation von Vektoren erhalten wir die Zahl: $$$(1 \ times k) \ centerdot (k \ times 1) = 1 \ times 1$ wie erwartet. Diese Zahl ist die Annäherung " $$$i$ -th "Ziel. Aber wir müssen nicht einen Wert des Ziels approximieren, sondern alle. Dazu schreiben wir alles" $$$i$ Matrix-Regressoren $$$X$ . Die resultierende Matrix hat die Dimension $$$(n \ times k)$ :

$$$$ display $$ X = \ begin {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $$ display $$

Nun hat die lineare Regressionsgleichung die Form:

$$

$$f (w, X) = X \ vec {w}$$

Bezeichnen Sie die Werte der Zielindikatoren (alle $$$y_i$ ) pro Vektor $$$\ vec {y}$ Dimension $$$(n \ times 1)$ :

$$

$$\ vec {y} = \ begin {pmatrix} y_ {0} \\ y_ {1} \\ ... \\ y_ {n} \ end {pmatrix} \ qquad$$

Nun können wir im Matrixformat die Gleichung zur Beurteilung der Qualität eines linearen Modells schreiben:

$$

$$Err = (X \ vec {w} - \ vec {y}) ^ 2 \ rightarrow min$$

Tatsächlich erhalten wir aus dieser Formel weiterhin die uns bekannte Formel $$$X ^ T X w = X ^ T y$

Wie geht das? Die Klammern werden geöffnet, die Differenzierung wird durchgeführt, die resultierenden Ausdrücke werden transformiert usw. Und genau das werden wir jetzt tun.

Matrixtransformationen

Klappen Sie die Klammern auf

$$$(X \ vec {w} - \ vec {y}) ^ 2 = (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y})$

$$$= (X \ vec {w}) ^ TX \ vec {w} - \ vec {y} ^ TX \ vec {w} - (X \ vec {w}) ^ T \ vec {y} + \ vec { y} ^ T \ vec {y}$

Bereiten Sie eine Gleichung zur Differenzierung vor

Dazu führen wir einige Transformationen durch. In nachfolgenden Berechnungen wird es für uns praktischer sein, wenn der Vektor $$$\ vec {w} ^ T$ wird zu Beginn jeder Arbeit in der Gleichung vorgestellt.

Umwandlung 1

$$$\ vec {y} ^ TX \ vec {w} = (X \ vec {w}) ^ T \ vec {y} = \ vec {w} ^ TX ^ T \ vec {y}$

Wie ist es dazu gekommen? Um diese Frage zu beantworten, schauen Sie sich einfach die Größen der multiplizierten Matrizen an und sehen Sie, dass wir am Ausgang eine Zahl oder etwas anderes erhalten $$$const$ .

Wir schreiben die Dimensionen der Matrixausdrücke.

$$$\ vec {y} ^ TX \ vec {w}: (1 \ times n) \ centerdot (n \ times k) \ centerdot (k \ times 1) = (1 \ times 1) = const$

$$$(X \ vec {w}) ^ T \ vec {y}: ((n \ times k) \ centerdot (k \ times 1)) ^ T \ centerdot (n \ times 1) = (1 \ times n) \ centerdot (n \ times 1) = (1 \ times 1) = const$

$$$\ vec {w} ^ TX ^ T \ vec {y}: (1 \ mal k) \ centerdot (k \ mal n) \ centerdot (n \ mal 1) = (1 \ mal 1) = const$

Umwandlung 2

$$$(X \ vec {w}) ^ TX \ vec {w} = \ vec {w} ^ TX ^ TX \ vec {w}$

Wir schreiben ähnlich wie Transformation 1

$$$(X \ vec {w}) ^ TX \ vec {w}: ((n \ mal k) \ centerdot (k \ mal 1)) ^ T \ centerdot (n \ mal k) \ centerdot (k \ mal 1 ) = (1 \ mal 1) = const$

$$$\ vec {w} ^ TX ^ TX \ vec {w}: (1 \ mal k) \ centerdot (k \ mal n) \ centerdot (n \ mal k) \ centerdot (k \ mal 1) = (1 \ mal 1) = const$

Am Ausgang erhalten wir eine Gleichung, die wir unterscheiden müssen:
$$$Err = \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

Wir unterscheiden die Funktion der Bewertung der Qualität des Modells

Unterscheiden nach Vektor $$$\ vec {w}$ :

$$

$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}}$$

$$$(\ vec {w} ^ TX ^ TX \ vec {w}) '- (2 \ vec {w} ^ TX ^ T \ vec {y})' + (\ vec {y} ^ T \ vec {y }) '= 0$

$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} + 0 = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

Fragen warum $$$(\ vec {y} ^ T \ vec {y}) '= 0$ Sollte dies nicht der Fall sein, aber die Operationen zur Bestimmung der Ableitungen in den beiden anderen Ausdrücken werden wir genauer analysieren.

Differenzierung 1

Wir zeigen die Unterscheidung: $$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w})} {d \ vec {w}} = 2X ^ TX \ vec {w}$

Um die Ableitung einer Matrix oder eines Vektors zu bestimmen, müssen Sie sehen, was sie enthalten. Wir schauen:

$$$ inline $ \ vec {w} ^ T = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$\ vec {w} = \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$

$$$ inline $ X ^ T = \ begin {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} & x_ {11} & ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $$$ $ inline $ X = \ begin {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $

Bezeichnen Sie das Produkt von Matrizen $$$X ^ TX$ durch die Matrix $$$A$ . Matrix $$$A$ quadratisch und darüber hinaus ist es symmetrisch. Diese Eigenschaften werden uns weiterhin nützlich sein, merken Sie sich diese. Matrix $$$A$ hat Dimension $$$(k \ times k)$ :

$$$ inline $ A = \ begin {pmatrix} a_ {00} & a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad $ inline $

Jetzt ist es unsere Aufgabe, die Vektoren korrekt mit der Matrix zu multiplizieren und nicht "zweimal zwei fünf" zu erhalten, also werden wir uns konzentrieren und äußerst vorsichtig sein.

$$$ inline $ \ vec {w} ^ TA \ vec {w} = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad \ times \ begin {pmatrix} a_ {00} & a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \ \ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$ inline $ = \ begin {pmatrix} w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0} & ... & w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk} \ end {pmatrix} \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$= \ begin {pmatrix} (w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0}) w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu (w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk}) w_k \ end {pmatrix} =$

$$$= w_0 ^ 2a_ {00} + w_1a_ {10} w_0 + w_ka_ {k0} w_0 \ mkern 10 mu + \ mkern 10 mu ... \ mkern 10 mu + \ mkern 10 mu w_0a_ {0 k} w_k + w_1a_ {1 k} w_k + .. . + w_k ^ 2a_ {kk}$

Wir haben jedoch einen komplizierten Ausdruck! Tatsächlich haben wir eine Zahl - einen Skalar. Und jetzt gehen wir schon wirklich zur Differenzierung über. Es ist notwendig, die Ableitung des erhaltenen Ausdrucks für jeden Koeffizienten zu finden $$$w_0 w_1 ... w_k$ und den Dimensionsvektor am Ausgang erhalten $$$(k \ times 1)$ . Nur für den Fall werde ich die Vorgehensweisen für die Aktionen beschreiben:

1) differenzieren durch $$$w_o$ wir bekommen: $$$2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k}$

2) differenzieren durch $$$w_1$ wir bekommen: $$$w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ {k}$

3) differenzieren durch $$$w_k$ wir bekommen: $$$w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k-1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk}$

Am Ausgang der versprochene Größenvektor $$$(k \ times 1)$ :

$$

$$\ begin {pmatrix} 2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k} \\ w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ { k} \\ ... \\ ... \\ ... \\ w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k -1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk} \ end {pmatrix}$$

Wenn Sie sich den Vektor genauer ansehen, werden Sie feststellen, dass das linke und das entsprechende rechte Element des Vektors so gruppiert werden können, dass der Vektor vom dargestellten Vektor unterschieden werden kann $$$\ vec {w}$ die Größe $$$(k \ times 1)$ . Zum Beispiel $$$w_1a_ {10}$ (linkes Element der obersten Zeile des Vektors) $$$+ a_ {01} w_1$ (das rechte Element der obersten Zeile des Vektors) kann als dargestellt werden $$$w_1 (a_ {10} + a_ {01})$ und $$$w_2a_ {20} + a_ {02} w_2$ - wie $$$w_2 (a_ {20} + a_ {02})$ usw. in jeder Zeile. Gruppe:

$$

$$\ begin {pmatrix} 2w_0a_ {00} + w_1 (a_ {10} + a_ {01}) + w_2 (a_ {20} + a_ {02}) + ... + w_k (a_ {k0} + a_ { 0k}) \\ w_0 (a_ {01} + a_ {10}) + 2w_1a_ {11} + w_2 (a_ {21} + a_ {12}) + ... + w_k (a_ {k1} + a_ {1k }) \\ ... \\ ... \\ ... \\ w_0 (a_ {0k} + a_ {k0}) + w_1 (a_ {1k} + a_ {k1}) + w_2 (a_ {2k } + a_ {k2}) + ... + 2w_ka_ {kk} \ end {pmatrix}$$

Nehmen Sie den Vektor heraus $$$\ vec {w}$ und am Ausgang erhalten wir:

$$$$ display $$ \ begin {pmatrix} 2a_ {00} & a_ {10} + a_ {01} & a_ {20} + a_ {02} & ... & a_ {k0} + a_ {0k} \\ a_ {01} + a_ {10} & 2a_ {11} & a_ {21} + a_ {12} & ... & a_ {k1} + a_ {1k} \\ ... & ... & .. . & ... & ... \\ ... & ... & ... & ... & ... \\ ... & ... & ... & ... & .. . \\ a_ {0k} + a_ {k0} & a_ {1k} + a_ {k1} & a_ {2k} + a_ {k2} & ... & 2a_ {kk} \ end {pmatrix} \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ ... \\ ... \\ w_k \ end {pmatrix} \ qquad $$ display $$

Schauen wir uns nun die resultierende Matrix an. Eine Matrix ist die Summe zweier Matrizen $$$A + A ^ T$ :

$$$$ display $$ \ begin {pmatrix} a_ {00} & a_ {01} & a_ {02} & ... & a_ {0k} \\ a_ {10} & a_ {11} & a_ {12} & ... & a_ {1k} \\ ... & ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & a_ {k2} & ... & a_ {kk} \ end {pmatrix} + \ begin {pmatrix} a_ {00} & a_ {10} & a_ {20} & ... & a_ {k0} \\ a_ {01} & a_ {11} & a_ {21} & ... & a_ {k1} \\ ... & ... & ... & ... & ... \\ a_ {0k} & a_ {1k} & a_ {2k} & ... & a_ {kk} \ end {pmatrix} \ qquad $$ display $$

Denken Sie daran, dass wir vorhin eine wichtige Eigenschaft der Matrix festgestellt haben $$$A$ - Es ist symmetrisch. Anhand dieser Eigenschaft können wir sicher den Ausdruck angeben $$$A + A ^ T$ gleich $$$2A$ . Dies lässt sich leicht überprüfen, indem das Produkt Matrix für Element angezeigt wird $$$X ^ TX$ . Wir werden dies hier nicht tun, wer möchte, kann die Überprüfung selbst durchführen.

Kommen wir zu unserem Ausdruck zurück. Nach unseren Transformationen stellte sich heraus, wie wir es sehen wollten:

$$

$$(A + A ^ T) \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = 2A \ vec {w} = 2X ^ TX \ vec {w}$$

Also haben wir die erste Differenzierung gemeistert. Wir kommen zum zweiten Ausdruck.

Differenzierung 2

$$$\ frac {d (2 \ vec {w} ^ TX ^ T \ vec {y})} {d \ vec {w}} = 2X ^ T \ vec {y}$

Gehen wir den ausgetretenen Pfaden entlang. Es wird viel kürzer als das vorherige sein, gehen Sie also nicht weit vom Bildschirm weg.

Wir decken die elementweisen Vektoren und die Matrix auf:

$$$ inline $ \ vec {w} ^ T = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$ inline $ X ^ T = \ begin {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} & x_ {11} & ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $

$$$\ vec {y} = \ begin {pmatrix} y_0 \\ y_1 \\ ... \\ y_n \ end {pmatrix} \ qquad$

Für eine Weile entfernen wir die Zwei aus den Berechnungen - es spielt keine große Rolle, dann werden wir es an seinen Platz zurückbringen. Multiplizieren Sie die Vektoren mit der Matrix. Zunächst multiplizieren wir die Matrix $$$X ^ T$ auf vektor $$$\ vec {y}$ Hier haben wir keine Einschränkungen. Holen Sie sich den Größenvektor $$$(k \ times 1)$ :

$$

$$\ begin {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

Führen Sie die folgende Aktion aus - multiplizieren Sie den Vektor $$$\ vec {w}$ zu dem resultierenden Vektor. Am Ausgang wartet eine Nummer auf uns:

$$

$$\ begin {pmatrix} w_0 (x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n) + w_1 (x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1 } y_n) \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_k (x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n) \ end {pmatrix} \ qquad$$

Wir unterscheiden es dann. Am Ausgang erhalten wir einen Dimensionsvektor $$$(k \ times 1)$ :

$$

$$\ begin {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

Ähnelt es etwas? Alles ist richtig! Dies ist das Produkt der Matrix. $$$X ^ T$ auf vektor $$$\ vec {y}$ .

Damit wurde die zweite Unterscheidung erfolgreich abgeschlossen.

Anstelle einer Schlussfolgerung

Jetzt wissen wir, wie es zur Gleichstellung kam. $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ .

Schließlich beschreiben wir einen schnellen Weg, um die Hauptformeln zu transformieren.

Schätzen Sie die Qualität des Modells nach der Methode der kleinsten Quadrate:
$$$\ sum \ limits_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ mkern 20mu = \ mkern 20mu \ sum \ limits_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 =$

$$$= (X \ vec {w} - \ vec {y}) ^ 2 \ mkern 20 mu = \ mkern 20 mu (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y}) \ mkern 20mu = \ mkern 20mu \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

Wir differenzieren den resultierenden Ausdruck:
$$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}} =$$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

$$$\ leftarrow$ Frühere Arbeiten des Autors - „Wir lösen die Gleichung der einfachen linearen Regression“
$$$\ rightarrow$ Die nächste Arbeit des Autors - "Chewing Logistic Regression"

Literatur

Internetquellen:

1) habr.com/de/post/278513
2) habr.com/ru/company/ods/blog/322076
3) habr.com/de/post/307004
4) nabatchikov.com/blog/view/matrix_der

Lehrbücher, Aufgabensammlungen:

1) Vorlesungsskript über höhere Mathematik: volle Lehrveranstaltung / D.T. Geschrieben - 4. Aufl. - M .: Iris Press, 2006
2) Angewandte Regressionsanalyse / N. Draper, G. Smith - 2. Aufl. - M .: Finanzen und Statistik, 1986
3) Aufgaben zum Lösen von Matrixgleichungen:
function-x.ru/matrix_equations.html
mathprofi.ru/deistviya_s_matricami.html