Beim Extrahieren von Informationen stellt sich häufig die Aufgabe, solche Textfragmente zu finden. Im Rahmen einer Suche kann eine Abfrage vom Benutzer (z. B. dem Text, den der Benutzer in die Suchmaschine eingibt) oder vom System selbst generiert werden. Oft müssen wir eine eingehende Abfrage mit bereits indizierten Abfragen abgleichen. In diesem Artikel wird untersucht, wie Sie ein System erstellen können, das dieses Problem in Bezug auf Milliarden von Anforderungen löst, ohne ein Vermögen für die Serverinfrastruktur auszugeben.

Zunächst definieren wir das Problem formell:

Angesichts eines festen Satzes von Abfragen $$$Q$ eingehende Anfrage $$$q$ und eine ganze Zahl $$$k$ . Müssen eine solche Untermenge von Abfragen finden $$$R = \ left \ {q0, q1, ..., qk \ right \} \ subset Q$ zu jeder Anfrage $$$q_ {i} \ in R$ war eher wie $$$q$ als jede andere Anfrage in $$$Q ∖ R$ .

Zum Beispiel mit diesem Satz von Abfragen $$$Q$ :

{tesla cybertruck, beginner bicycle gear, eggplant dishes, tesla new car, how expensive is cybertruck, vegetarian food, shimano 105 vs ultegra, building a carbon bike, zucchini recipes} 

und $$$k = 3$ Sie können folgendes Ergebnis erwarten:


Bitte beachten Sie, dass wir noch kein Ähnlichkeitskriterium definiert haben. In diesem Zusammenhang kann dies fast alles bedeuten, aber es kommt normalerweise auf eine Art von Ähnlichkeit an, die auf Schlüsselwörtern oder Vektoren basiert. Mithilfe der keyword-basierten Ähnlichkeit können wir zwei ähnliche Abfragen finden, wenn sie genügend gemeinsame Wörter enthalten. Zum Beispiel sind die Abfragen „Ein Restaurant in München eröffnen“ und „Bestes Restaurant in München“ ähnlich, weil sie die Wörter „Restaurant“ und „München“ enthalten. Und die Fragen „bestes restaurant münchens“ und „wo man in münchen isst“ sind schon weniger ähnlich, weil sie nur ein gemeinsames wort haben. Wer in München ein Restaurant sucht, ist jedoch besser aufgehoben, wenn sich das zweite Anforderungspaar als ähnlich herausstellt. Und dabei helfen wir dem Vergleich anhand von Vektoren.

Vektordarstellung von Wörtern

Die Vektordarstellung von Wörtern ist eine maschinelle Lerntechnik, die bei der Verarbeitung natürlicher Sprachen verwendet wird, um Text oder Wörter in Vektoren umzuwandeln. Wenn wir die Aufgabe in den Vektorraum verschieben, können wir mathematische Operationen mit Vektoren verwenden - Summieren und Berechnen von Entfernungen. Um Verknüpfungen zwischen ähnlichen Wörtern herzustellen, können Sie herkömmliche Methoden der Vektorclusterung verwenden. Die Bedeutung dieser Operationen im ursprünglichen Wortraum mag nicht offensichtlich sein, aber der Vorteil ist, dass wir jetzt Zugriff auf eine breite Palette von mathematischen Werkzeugen haben. Wenn Sie an Details zu Wortvektoren und deren Anwendung interessiert sind, lesen Sie mehr über word2vec und GloVe .

Wir haben eine Möglichkeit, Vektoren aus Wörtern zu generieren. Jetzt sammeln wir sie in Textvektoren (Vektoren von Dokumenten oder Ausdrücken). Der einfachste Weg, dies zu tun, ist das Hinzufügen (oder Mitteln) der Vektoren aller Wörter im Text.


^{Abbildung 1: Abfragevektoren}

Jetzt können Sie die Ähnlichkeit zweier Textteile (oder Abfragen) ermitteln, indem Sie sie im Vektorraum darstellen und den Abstand zwischen den Vektoren berechnen. Typischerweise wird hierfür ein Winkelabstand verwendet.

Infolgedessen ermöglicht die Vektordarstellung von Wörtern einen Textabgleich eines anderen Typs, der den schlüsselwortbasierten Abgleich ergänzt. Sie können die semantische Ähnlichkeit von Anfragen (zum Beispiel "bestes Restaurant in München" und "wo man in München essen kann") untersuchen, wie wir es vorher nicht konnten.

Ungefähre Suche nach nächstem Nachbarn

Jetzt können wir unser ursprüngliches Abfragezuordnungsproblem verfeinern:

Gegeben eine feste Menge von Abfragevektoren $$$Q$ eingehender Vektor $$$q$ und eine ganze Zahl $$$k$ . Sie müssen eine solche Untergruppe von Vektoren finden $$$R = \ left \ {q0, q1, ..., qk \ right \} \ subset Q$ so dass der Winkelabstand von $$$q$ zu jedem Vektor $$$q_ {i} \ in R$ war kürzer als der Abstand zu einem anderen Vektor in $$$Q ∖ R$ .

Dies nennt man die Aufgabe, den nächsten Nachbarn zu finden. Es gibt eine Reihe von Algorithmen für die schnelle Lösung in niedrigdimensionalen Räumen. Wenn wir jedoch mit Vektordarstellungen von Wörtern arbeiten, arbeiten wir normalerweise mit hochdimensionalen Vektoren (100-1000 Dimensionen). Und hier funktionieren die genannten Methoden nicht mehr.

Es gibt keine geeignete Möglichkeit, die nächsten Nachbarn in hochdimensionalen Räumen schnell zu ermitteln. Daher vereinfachen wir das Problem, indem wir die Verwendung von Näherungsergebnissen zulassen: Anstatt immer die nächsten Vektoren zurückzugeben, begnügen wir uns nur mit einigen der nächsten oder zu einem gewissen Grad nahen Nachbarn. Dies wird als ungefähre Suche nach dem nächsten Nachbarn bezeichnet und ist ein Bereich aktiver Forschung.

Hierarchische kleine Welt

Der Hierarchical Navigable Small-World Graph ( HNSW ) ist einer der schnellsten Algorithmen für die ungefähre Suche nach nächsten Nachbarn. Der Suchindex in HNSW ist eine mehrstufige Struktur, bei der jede Stufe ein Proximity-Diagramm ist. Jeder Graphknoten entspricht einem der Abfragevektoren.


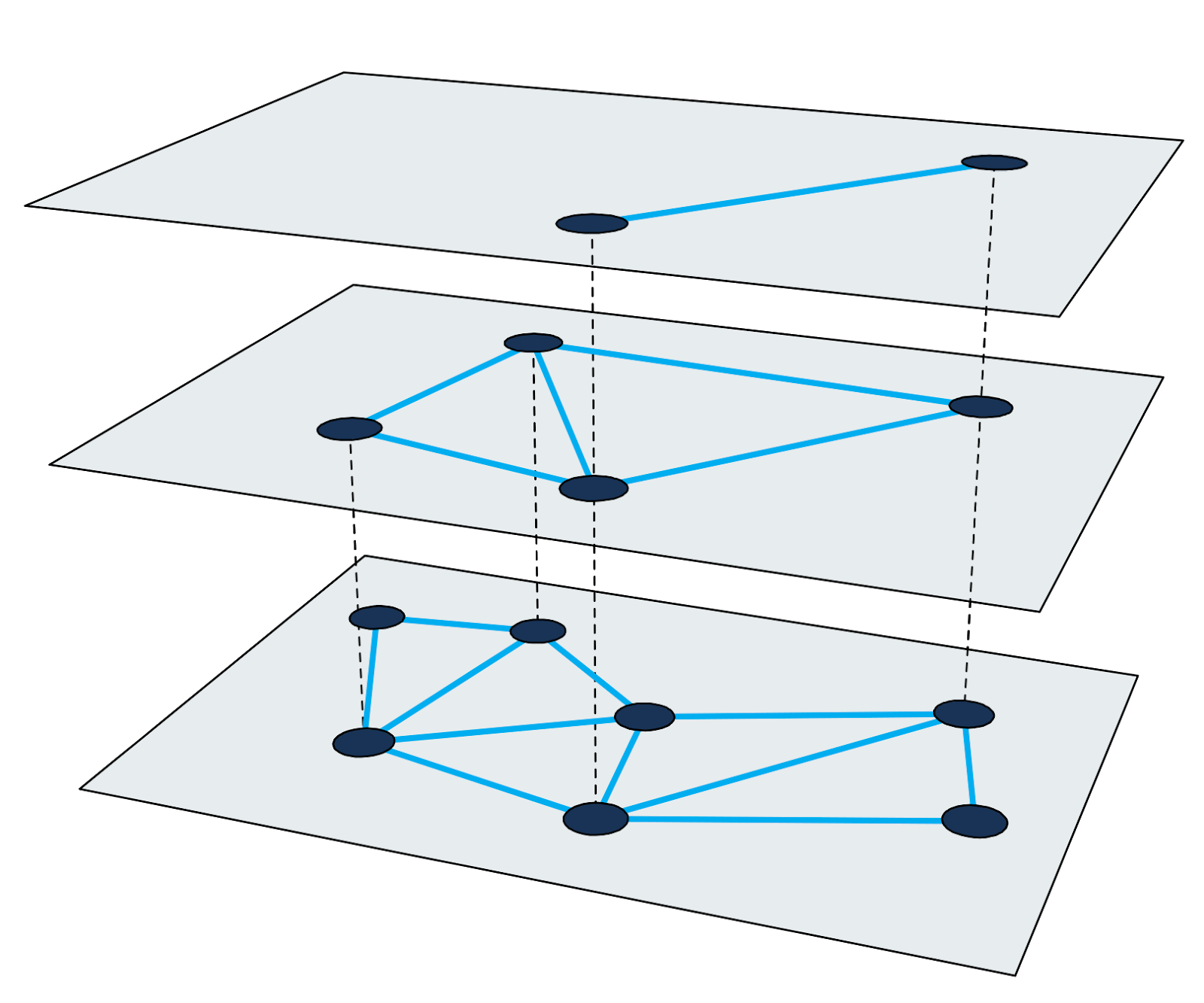^{Abbildung 2: Mehrstufiges Proximity-Diagramm.}
Die Suche nach nächstgelegenen Nachbarn in HNSW verwendet die Zoom-In-Methode. Es startet im Eingangsknoten der höchsten Ebene und führt auf jeder Ebene rekursiv eine gierige Grafikdurchquerung durch, bis es unten ein lokales Minimum erreicht.

Details zum Algorithmus und zur Suchtechnik sind in der wissenschaftlichen Arbeit gut beschrieben. Es ist wichtig, sich daran zu erinnern, dass jeder Suchzyklus nach den nächsten Nachbarn darin besteht, die Knoten der Graphen zu durchlaufen und die Abstände zwischen den Vektoren zu berechnen. In den folgenden Schritten wird anhand dieser Methode ein umfangreicher Index erstellt.

Die Schwierigkeit, Milliarden von Abfragen zu indizieren

Angenommen, wir müssen 4 Milliarden 200-dimensionale Abfragevektoren indizieren, wobei jede Dimension durch eine 4-Byte-Gleitkommazahl dargestellt wird (4 Milliarden reichen aus, um die Aufgabe interessant zu machen, aber Sie können die Knoten-IDs weiterhin in regulären 4-Byte-Zahlen speichern). . Eine grobe Berechnung sagt uns, dass die Größe der Vektoren alleine etwa 3 TB beträgt. Da die meisten vorhandenen Bibliotheken eine RAM-Kapazität für die ungefähre Suche nach den nächsten Nachbarn verwenden, benötigen wir einen sehr großen Server, um mindestens Vektoren in den RAM zu übertragen. Bitte beachten Sie, dass hierbei der zusätzliche Suchindex nicht berücksichtigt wird, der für die meisten Methoden erforderlich ist.

In der gesamten Entwicklungsgeschichte unserer Suchmaschine haben wir dieses Problem auf verschiedene Weise gelöst. Betrachten wir einige davon.

Teilmenge von Daten

Der erste und einfachste Ansatz, mit dem wir das Problem nicht vollständig lösen konnten, bestand darin, die Anzahl der Vektoren im Index zu begrenzen. Aus einem Zehntel der Daten haben wir einen Index erstellt, der - überraschend - 10% des Speichers benötigt. Die Qualität der Suche hat sich jedoch verschlechtert, da wir jetzt mit weniger Abfragen gearbeitet haben.

Quantisierung

Hier verwendeten wir alle Daten, reduzierten sie jedoch mithilfe der Quantisierung (wir verwendeten verschiedene Quantisierungstechniken, z. B. die Produktquantisierung, konnten jedoch mit dieser Datenmenge nicht die gewünschte Arbeitsqualität erzielen). Durch Abrunden einiger Fehler konnten wir alle Vier-Byte-Zahlen in den ursprünglichen Vektoren durch quantisierte Einzel-Byte-Versionen ersetzen. Die RAM-Größe für Vektoren verringerte sich um 75%. Wir benötigten jedoch immer noch 750 GB Arbeitsspeicher (ohne die Größe des Index selbst), und dies ist immer noch ein sehr großer Server.

Speicherprobleme mit Granne lösen

Die beschriebenen Ansätze hatten ihre Vorteile, erforderten jedoch viel Ressourcen und ergaben eine schlechte Suchqualität. Obwohl es Bibliotheken gibt , die in weniger als 1 ms antworten, können wir die Geschwindigkeit gegen geringere Hardwareanforderungen eintauschen.

Granne (graphenbasierte ungefähre nächste Nachbarn) ist eine HNSW-Bibliothek, die von Cliqz für die Suche nach solchen Abfragen entwickelt und verwendet wird. Es hat Open Source Code, aber die Bibliothek befindet sich noch in der aktiven Entwicklung. Eine verbesserte Version wird 2020 auf crates.io veröffentlicht. Es ist in Rust mit Python-Inserts geschrieben, die so konzipiert sind, dass Milliarden von Vektoren wettbewerbsfähig sind. Aus Sicht der Abfragevektoren ist es interessant, dass Granne über einen speziellen Modus verfügt, der im Vergleich zu anderen Bibliotheken viel weniger Speicher benötigt.

Kompakte Darstellung von Abfragevektoren

Das Reduzieren der Größe von Abfragevektoren bringt uns viele Vorteile. Lassen Sie uns dazu zurückgehen und überlegen, Vektoren zu erstellen. Da Abfragen aus Wörtern bestehen und Abfragevektoren Summen von Wortvektoren sind, können wir ausdrücklich ablehnen, Abfragevektoren zu speichern und sie nach Bedarf zu berechnen.

Sie können Abfragen in Form von Wortmengen speichern und anhand der Nachschlagetabelle die entsprechenden Vektoren finden. Wir vermeiden jedoch eine Umleitung, indem wir jede Abfrage als Liste von Ganzzahl-IDs speichern, die den Wortvektoren in der Abfrage entsprechen. Speichern Sie beispielsweise die Abfrage „bestes Restaurant Münchens“ als $$$[{i_ {best}}, {i_ {restaurant}}, {i_ {of}}, {i_ {munich}}]$ wo $$${i_ {best}}$ - Dies ist die Vektor-ID des Wortes "best" usw. Angenommen, wir haben weniger als 16 Millionen Wortvektoren (mehr als 1 Byte pro Wort), dann können Sie 3 Byte verwenden, um alle Wort-IDs darzustellen. Das heißt, anstatt 800 Bytes (oder 200 Bytes bei quantisierten Vektoren) zu speichern, werden für diese Anforderung nur 12 Bytes gespeichert (Dies ist nicht ganz richtig. Da die Anforderungen aus einer anderen Anzahl von Wörtern bestehen, müssen wir auch den Listenoffset im Wortindex speichern. Für Dies erfordert 5 Bytes pro Anforderung.

Die Wortvektoren brauchen wir alle. Die Anzahl der Wörter ist jedoch viel kleiner als die Anzahl der Abfragen, die durch Kombinieren dieser Wörter erstellt werden können. Und das bedeutet, dass die Größe der Wörter nicht so wichtig ist. Wenn Sie Wortvektoren als 4-Byte-Gleitkommaversionen in einem einfachen Array speichern $$$v$ Dann brauchen wir weniger als 1 GB für jede Million Wörter. Dieses Volume passt problemlos in den Arbeitsspeicher. Nun sieht der Abfragevektor so aus: $$${v _ {{i_ {best}}} + {v _ {{i_ {restaurant}} + {v _ {{i_ {of}} + {v _ {{i_ {münchen}}}$ .

Die endgültige Größe der Abfrageübermittlung hängt von der Gesamtzahl der Wörter in der Abfrage ab. Für 4 Milliarden Abfragen sind dies etwa 80 GB (einschließlich Wortvektoren). Mit anderen Worten, verglichen mit den ursprünglichen Wortvektoren verringerte sich die Größe um 97% und verglichen mit quantisierten Vektoren um 90%.

Und noch eine Sache. Für eine Suche müssen ungefähr 200-300 Knoten des Graphen besucht werden. Jeder Knoten hat 20-30 Nachbarn. Wir müssen also den Abstand vom Eingabeabfragevektor zu 4000-9000 Vektoren im Index berechnen. Außerdem müssen Vektoren generiert werden. Wie lange dauert es, um Abfragevektoren im laufenden Betrieb zu erstellen?

Es stellt sich heraus, dass dieses Problem mit einem relativ neuen Prozessor in wenigen Millisekunden gelöst werden kann. Eine Anforderung, die früher in 1 ms ausgeführt wurde, dauert jetzt ungefähr 5 ms. Dann haben wir den Speicher für Vektoren um 90% reduziert. Einen solchen Kompromiss haben wir gerne angenommen.

Anzeige im Speicher von Vektoren und Index

Oben haben wir das Problem der Reduzierung des Speichers für Vektoren gelöst. Nachdem wir dieses Problem gelöst hatten, wurde die Indexstruktur selbst zu einem einschränkenden Faktor. Jetzt müssen Sie die Größe reduzieren.

In Granne wird die Graphenstruktur kompakt in Form einer Adjazenzliste mit einer variablen Anzahl von Nachbarn für jeden Knoten gespeichert. Das heißt, Speicherplatz wird kaum für Metadaten verschwendet. Die Größe der Indexstruktur hängt stark von den Entwurfsparametern und den Diagrammeigenschaften ab. Um eine Vorstellung von der Größe des Index zu bekommen, reicht es jedoch zu sagen, dass wir einen Index für 4 Milliarden Vektoren mit einer Gesamtgröße von ca. 240 GB erstellen können. Dies ist möglicherweise für die Verwendung im Arbeitsspeicher auf einem großen Server akzeptabel, kann jedoch besser durchgeführt werden.


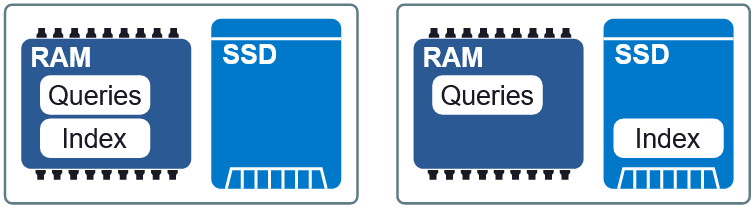^{Abbildung 3: Zwei verschiedene Layouts in RAM und SSD.}

Eine wichtige Eigenschaft von Granne ist die Fähigkeit, die Index- und Abfragevektoren im Speicher anzuzeigen . Dies ermöglicht es uns, den Index träge zu laden und den Speicher mit mehreren Prozessen gemeinsam zu nutzen. Die Index- und Abfragedateien sind in separate Anzeigedateien im Speicher unterteilt und können in verschiedenen Layouts im RAM und auf der SSD verwendet werden. Wenn die Anforderungen für die Verzögerung etwas geringer sind, stellen Sie den Index auf die SSD und fordern Sie RAM an. Wir behalten eine akzeptable Geschwindigkeit bei, ohne übermäßigen Speicherverbrauch. Am Ende des Artikels werden wir sehen, wie dieser Kompromiss aussieht.

Verbesserung der Datenlokalität

In unserer aktuellen Konfiguration erfordert jede Anforderung, wenn sich der Index auf einer SSD befindet, bis zu 200-300 Lesevorgänge von der Festplatte. Sie können versuchen, die Lokalität der Daten zu erhöhen, indem Sie die Elemente anordnen, deren Vektoren so nahe beieinander liegen, dass sich ihre HNSW-Knoten ebenfalls nicht weit voneinander entfernt im Index befinden. Die Datenlokalität verbessert die Leistung, da ein einzelner Lesevorgang (normalerweise aus 4 KB extrahiert) mit größerer Wahrscheinlichkeit andere Knoten enthält, die zum Durchlaufen des Diagramms erforderlich sind. Dies wiederum reduziert die Anzahl der Datenabrufe pro Suche.


^{Abbildung 4: Datenlokalität reduziert das Abrufen von Informationen.}

Es sollte beachtet werden, dass das Umordnen von Elementen keine Auswirkungen auf die Suchergebnisse hat. Dies ist eine Möglichkeit, die Suche zu beschleunigen. Das heißt, die Reihenfolge kann beliebig sein, aber nicht jede Option beschleunigt die Suche. Es ist sehr schwierig, die optimale Reihenfolge zu finden. Die Heuristik, die wir erfolgreich angewendet haben, besteht jedoch darin, die Abfragen nach dem wichtigsten Wort in jeder Abfrage zu sortieren.

Fazit

Wir verwenden Granne zum Erstellen und Verwalten von milliardenschweren Indizes mit Abfragevektoren, um nach ähnlichen Abfragen mit relativ geringem Speicherverbrauch zu suchen. Die folgende Tabelle zeigt die Anforderungen für verschiedene Methoden. Seien Sie skeptisch in Bezug auf die absoluten Werte von Verzögerungen während der Suche, da diese stark von der als akzeptabel geltenden Antwort abhängen. Diese Informationen beschreiben jedoch die relative Leistung der Methoden.


* Das Zuweisen eines Speicherindexes, der größer als die erforderliche Menge ist, führte zum Zwischenspeichern einiger (häufig besuchter) Knoten, wodurch die Verzögerung bei der Suche verringert wurde. Hierfür wurde kein interner Cache verwendet, sondern nur interne OS-Tools (Linux-Kernel).

Es ist zu beachten, dass einige der im Artikel erwähnten Optimierungen nicht zur Lösung des allgemeinen Problems der Suche nach nächsten Nachbarn mit nicht zusammensetzbaren Vektoren anwendbar sind. Sie sind jedoch in allen Situationen anwendbar, in denen Elemente aus weniger Teilen generiert werden können (wie dies bei Wörtern und Abfragen der Fall ist). Ansonsten können Sie Granne immer noch mit den Quellvektoren verwenden, es wird nur mehr Speicher benötigt, als bei anderen Bibliotheken.