Guten Tag!
In diesem Artikel werde ich versuchen, einen neuen Blick auf den Algorithmus zu werfen, um eine allgemeine Lösung für ein lineares Gleichungssystem zu finden.
Die Aufgabe, die wir erledigen werden, klingt wie folgt.
Finden Sie eine allgemeine Lösung für das folgende Gleichungssystem
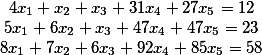
Dieses Problem wird gelöst, indem das Anfangssystem nach der Gauß-Methode in eine Dreiecksform gebracht wird. Wenn Sie dann freie Variablen auswählen, wird die allgemeine Lösung berechnet.
Ich möchte zeigen, wie man solche Systeme auf andere Weise lösen kann. Soweit es bekannt ist und woanders angewendet wird, konnte ich es nicht herausfinden. In allen öffentlichen / populären Materialien wird die Gauß-Methode verwendet.
Ich muss gleich sagen, dass die Lösung (in Bezug auf die Geschwindigkeit) sicherlich nicht optimal ist, da bei der Berechnung eines Vektorprodukts die Determinante der Matrix berechnet werden muss, und dies ist in gewisser Weise die Berechnung der Dreiecksmatrix.
Aber die Lösung ist schön und klar, außerdem ist das Kriterium, unter dem das System keine Lösungen hat, leicht zu erkennen.
Was ist das Wesen der Technik?
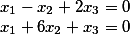
Wenn wir dieses System als Produkt zweier Vektoren lösen, erhalten wir
i%20+%20(%201%20)j%20+%20(%207%20)k)
Daher sind die Wurzeln des Systems gleich
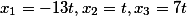
Für diejenigen, die nicht glauben, ist dies leicht durch Substitution zu überprüfen.
Wir wenden diese Technik an und überlegen, wie solche Systeme unter Verwendung von Vektorprodukten gelöst werden.
Wir haben also das Quellsystem
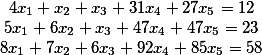
Verschieben Sie die freien Begriffe nach links
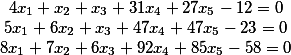
Wir haben 6 Spalten.
Zu diesem Zeitpunkt werden wir keine neuen Entitäten einführen und die Konzepte des Matrix-Rangs in unserer Arbeit nicht verwenden. (Bitte behandeln Sie mich herablassend)
Wir sehen nur, dass es 3 Gleichungen und 5 Variablen gibt. Daher werden in der allgemeinen Lösung 5-3 = 2 unabhängige Variablen verwendet.
Im selben Schritt können wir bestimmen, welche der Variablen frei sein wird. Wir nehmen zwei Variablen, die rechts von allen stehen, und setzen sie frei.
Hinweis: Bei anderen Gleichungen stellt sich nicht immer heraus, dass nur die letzten richtigen Koeffizienten verwendet werden müssen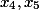
Und jetzt bestimmen wir in drei Schritten die grundlegende Lösung des ursprünglichen Systems
Schritt 1. Hier ist die letzte Spalte die freien Mitglieder des Systems.
i%20+%20(%20-162%20)j%20+%20(%20-486%20)k%20+%20(%20-81%20)l)
Schritt 2. Hier ist die letzte Spalte die Koeffizienten für die Variable
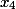
i%20+%20(%20162%20)j%20+%20(%20405%20)k%20+%20(%20-81%20)l)
Schritt 3. Hier ist die letzte Spalte die Koeffizienten für die Variable
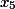
i%20+%20(%20243%20)j%20+%20(%20324%20)k%20+%20(%20-81%20)l)
Es ist nicht erforderlich, im Detail zu sagen, woher wir die Daten beziehen. Ich denke, das ist für die Leser offensichtlich. (Wer das Gleichungssystem mit der Cramer-Methode löst, findet Gemeinsamkeiten)
Interessanter ist, was wir mit diesen „Vektoren“ machen werden.
Teilen Sie sie durch -81
Wir erhalten die folgenden drei Vektoren
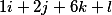
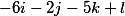
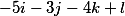
Ordnen Sie sie vertikal an, und die grundlegende Entscheidung nimmt die Form an
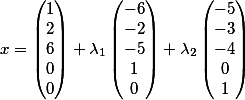
Großartig! Oder…
Für das Löslichkeitskriterium für ein gegebenes Gleichungssystem wird in den meisten Fällen die Kronecker-Copelli-Regel verwendet, hier wird einfach das Ergebnis des Vektorprodukts analysiert.
Wenn der resultierende Vektor die Form hat
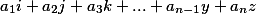
wo 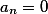 und unter allen verbleibenden gibt es mindestens eine Nicht-Null, dann hat ein solches System von Lösungen nichtWenn der resultierende Vektor alle Nullkoeffizienten aufweist, zeigt dies an, dass mindestens eine der Gleichungen eine lineare Darstellung der anderen ist und / oder eine der Variablen proportional zur anderen ist.
und unter allen verbleibenden gibt es mindestens eine Nicht-Null, dann hat ein solches System von Lösungen nichtWenn der resultierende Vektor alle Nullkoeffizienten aufweist, zeigt dies an, dass mindestens eine der Gleichungen eine lineare Darstellung der anderen ist und / oder eine der Variablen proportional zur anderen ist.Dieser Artikel ist der erste und ich würde gerne Kommentare, Kritik und Wünsche in meiner Ansprache hören.
Der Algorithmus und der Taschenrechner wurden
bereits im Januar 2019 erstellt , und erst heute habe ich beschlossen, Informationen über Habré zu veröffentlichen.
Wenn Sie in Ihrem Team / Ihrer Gesellschaft akzeptieren, wird das nächste Thema sein
- Wie finde ich eine allgemeine Lösung für das System der diophantinischen Gleichungen?