
Quantencomputer und Quantencomputer sind ein neues Schlagwort , das zusammen mit künstlicher Intelligenz , maschinellem Lernen und anderen High-Tech-Begriffen unserem Informationsraum hinzugefügt wurde. Gleichzeitig konnte ich im Internet kein Material finden, das mir ein Rätsel aufwirft, wie Quantencomputer funktionieren . Ja, es gibt viele ausgezeichnete Werke, darunter das Habré (siehe Ressourcenliste ), zu denen die Kommentare, wie es normalerweise der Fall ist, noch informativer und nützlicher sind, aber das Bild im Kopf stimmte nicht.
Kürzlich kamen Kollegen auf mich zu und fragten: „Verstehen Sie, wie ein Quantencomputer funktioniert? Kannst du es uns sagen? “Und dann wurde mir klar, dass das Problem mit dem Falten eines vollständigen Bildes in meinem Kopf nicht nur mein Problem ist.
Als Ergebnis wurde versucht, Informationen über Quantencomputer zu einem konsistenten logischen Schema zusammenzufassen, in dem auf einer grundlegenden Ebene ohne tiefes Eintauchen in die Mathematik und Struktur der Quantenwelt erklärt wurde, was ein Quantencomputer ist, auf welchen Prinzipien er arbeitet und mit welchen Problemen er konfrontiert ist Wissenschaftler bei seiner Schaffung und Betrieb.
Inhaltsverzeichnis
Haftungsausschluss
(zum Inhalt)
Der Autor ist kein Spezialist für Quantencomputer, und das Zielpublikum des Artikels sind dieselben IT-Experten, keine Quantenspezialisten , die auch ein Bild mit dem Titel „Wie Quantencomputer funktionieren“ in ihren Köpfen sammeln möchten. Aus diesem Grund werden viele Konzepte in dem Artikel bewusst vereinfacht, um ein besseres Verständnis der Quantentechnologien auf der "Basis" -Ebene zu erreichen, jedoch ohne große Vereinfachung mit dem Verlust von Informationsgehalt und Angemessenheit .
An einigen Stellen verwendet der Artikel Materialien aus anderen Quellen, deren Liste am Ende des Artikels angegeben ist . Wo immer möglich, werden direkte Links und Verweise auf den Originaltext, die Originaltabelle oder das Originalbild eingefügt. Wenn ich irgendwo etwas (oder jemanden) vergessen habe, schreibe - ich werde es korrigieren.
Einleitung
(zum Inhalt)
In diesem Kapitel werden wir kurz darauf eingehen, wie die Quantenära begann. Dies war die Motivation für die Idee eines Quantencomputers, der (welche Länder und Unternehmen) derzeit die führenden Akteure auf diesem Clearing sind, und wir werden kurz auf die Hauptrichtungen der Entwicklung des Quantencomputers eingehen.
Wie alles begann
(zum Inhalt)

Ausgangspunkt der Quantenära ist das Jahr 1900, als M. Planck erstmals die Hypothese aufstellte , dass Energie nicht kontinuierlich, sondern in getrennten Quanten (Portionen) emittiert und absorbiert wird. Die Idee wurde von vielen herausragenden Wissenschaftlern dieser Zeit aufgegriffen und weiterentwickelt - Bohr, Einstein, Heisenberg, Schrödinger, was letztendlich zur Schaffung und Entwicklung einer Wissenschaft wie der Quantenphysik führte . Es gibt viele gute Materialien zur Entwicklung der Quantenphysik als Wissenschaft im Internet, auf die wir in diesem Artikel nicht näher eingehen werden, aber es war notwendig, das Datum anzugeben, an dem wir in die neue Quantenära eingetreten sind.
Die Quantenphysik hat viele Erfindungen und Technologien in unser gewöhnliches Leben gebracht, ohne die es heute schwierig ist, sich die Welt um uns herum vorzustellen. Zum Beispiel ein Laser, der heute überall eingesetzt wird, von Haushaltsgeräten ( Laserpegel usw.) bis zu High-Tech-Systemen (Sehkorrekturlaser, Hallo Meklon ). Es wäre logisch anzunehmen, dass früher oder später jemand die Idee vorbringt, warum man Quantensysteme nicht für Berechnungen verwendet. Und so geschah es 1980.
Wikipedia weist darauf hin, dass der Wissenschaftler Yuri Manin 1980 als erster die Idee des Quantencomputers zum Ausdruck brachte. Aber erst 1981, als der bekannte R. Feynman in seinem Bericht auf der ersten Konferenz über Computerphysik am Massachusetts Institute of Technology feststellte, dass es unmöglich ist, die Entwicklung eines Quantensystems auf einem klassischen Computer auf effektive Weise zu modellieren. Er schlug ein Elementarmodell eines Quantencomputers vor , das eine solche Simulation durchführen könnte.
Es gibt eine solche Arbeit im Internet, in der die Chronologie der Entwicklung des Quantencomputers akademischer und detaillierter betrachtet wird, aber wir werden kurz darauf eingehen:
Meilensteine in der Geschichte der Quantencomputer:
Wie Sie sehen, sind 17 Jahre (von 1981 bis 1998) von der Idee bis zur ersten Implementierung in einem Computer mit 2 Qubits vergangen, und 21 Jahre (von 1998 bis 2019), bis die Anzahl der Qubits auf 53 angestiegen ist. Es dauerte 11 Jahre (von 2001 bis 2012), um das Ergebnis des Shore-Algorithmus von 15 auf 21 zu verbessern (wir werden weiter darauf eingehen). Auch kamen wir erst vor drei Jahren auf die Idee, worüber Feynman sprach, und lernen die einfachsten physikalischen Systeme zu simulieren.
Die Entwicklung des Quantencomputers ist langsam. Wissenschaftler und Ingenieure stehen vor sehr komplexen Aufgaben, Quantenzustände sind sehr kurzlebig und fragil, und um sie lange genug für Berechnungen zu halten, muss man Sarkophage für zig Millionen Dollar bauen, bei denen die Temperatur knapp über dem absoluten Nullpunkt gehalten wird und vor denen sie geschützt sind äußere Einflüsse. Weiter werden wir auf diese Aufgaben und Probleme näher eingehen.
Führende Spieler
(zum Inhalt)

Die Folien für diesen Abschnitt stammen aus dem Artikel Quantum Computer: A Big Boost Game. Vortrag in Yandex von einem Forscher am russischen Quantenzentrum Alexei Fedorov. Ich erlaube mir direkte Zitate:
Alle technologisch erfolgreichen Länder befassen sich derzeit aktiv mit der Entwicklung von Quantentechnologien. In diese Studien wird viel Geld investiert, spezielle Programme zur Unterstützung von Quantentechnologien entstehen.

Das Quantenrennen betrifft nicht nur Staaten, sondern auch Privatunternehmen. Insgesamt haben Google, IBM, Intel und Microsoft in den letzten Jahren rund 0,5 Milliarden US-Dollar in die Entwicklung von Quantencomputern investiert und große Labors und Forschungszentren geschaffen.
Es gibt viele Artikel über Habré und das Internet, zum Beispiel hier , hier und hier , in denen der aktuelle Stand der Entwicklung von Quantentechnologien in verschiedenen Ländern näher betrachtet wird. Für uns ist jetzt die Hauptsache, dass alle führenden technologisch entwickelten Länder und Akteure riesige Beträge in die Forschung in diese Richtung investieren, was Hoffnung auf einen Ausweg aus der gegenwärtigen technologischen Sackgasse gibt.
Entwicklungsrichtungen
(zum Inhalt)

Im Moment (ich kann mich irren, richtig) konzentrieren sich die Hauptanstrengungen (und die mehr oder weniger signifikanten Ergebnisse) für alle führenden Spieler auf zwei Richtungen:
- Spezialisierte Quantencomputer , die auf die Lösung eines bestimmten Problems abzielen, z. B. Optimierungsprobleme. Ein Beispiel für ein Produkt sind D-Wave-Quantencomputer.
- Universelle Quantencomputer - die beliebige Quantenalgorithmen (Shore, Grover usw.) implementieren können. Implementierungen von IBM, Google.
Andere Entwicklungsvektoren, die die Quantenphysik liefert, wie:
sicherlich auch in der Liste der Forschungsbereiche, aber es scheinen derzeit mehr oder weniger bedeutende Ergebnisse zu vorliegen.
Außerdem können Sie hier , hier und hier die Roadmap für die Entwicklung von Quantentechnologien lesen, also Google " Entwicklung von Quantentechnologien ".
Die Grundlagen. Quantenobjekt und Quantensysteme
(zum Inhalt)

Das Wichtigste, was Sie in diesem Abschnitt verstehen sollten, ist das Folgende
Ein Quantencomputer verwendet (im Gegensatz zu einem herkömmlichen) Quantenobjekte als Informationsträger, und Quantenobjekte müssen mit einem Quantensystem verbunden sein , um Berechnungen durchzuführen.
Was ist ein Quantenobjekt?
Ein Quantenobjekt ist ein Objekt der Mikrowelt (Quantenwelt), das Quanteneigenschaften aufweist:
- Hat einen bestimmten Zustand mit zwei Grenzniveaus
- Es befindet sich bis zum Zeitpunkt der Messung in einer Überlagerung seines Zustands
- Verwickelt mit anderen Objekten, um Quantensysteme zu erstellen
- Führt einen Satz zum Verbot des Klons durch (Sie können den Status eines Objekts nicht kopieren)
Lassen Sie uns jede Eigenschaft genauer analysieren:
Hat einen bestimmten Zustand mit zwei Grenzniveaus (Endzustand)
Ein klassisches Beispiel aus der realen Welt ist eine Münze. Sie hat einen Zustand von "Seite", der zwei Grenzstufen einnimmt - "Adler" und "Schwänze".
Es befindet sich bis zum Zeitpunkt der Messung in Überlagerung seines Zustands
Wirf eine Münze, sie fliegt und dreht sich. Während es sich dreht, ist es unmöglich zu sagen, in welcher der Randebenen sich sein "Seiten" -Zustand befindet. Aber wenn wir es zuschlagen und das Ergebnis betrachten, kollabiert die Überlagerung von Zuständen sofort in einen der beiden Grenzzustände - "Kopf" und "Zahl". In unserem Fall ist das Zuschlagen einer Münze eine Dimension.
Verwickelt mit anderen Objekten, um Quantensysteme zu erstellen
Mit einer Münze ist es schwierig, aber wir werden es versuchen. Stellen Sie sich vor, wir haben drei Münzen so geworfen, dass sie sich drehen und aneinander haften, so ein Jonglieren von Münzen. Zu jedem Zeitpunkt befindet sich nicht nur jeder von ihnen in einer Überlagerung von Zuständen, sondern diese Zustände beeinflussen sich gegenseitig (Münzen kollidieren).
Führt einen Satz zum Verbot des Klons durch (Sie können den Status eines Objekts nicht kopieren)
Während die Münzen fliegen und sich drehen, können wir in keiner Weise eine Kopie des Rotationszustands von Münzen erstellen, die vom System getrennt sind. Das System lebt in sich selbst und ist sehr eifersüchtig, Informationen weiterzugeben.
Ein paar Worte zum eigentlichen Konzept der „Überlagerung“ . In fast allen Artikeln wird die Überlagerung als „in allen Zuständen zur gleichen Zeit“ erklärt, was natürlich zutrifft, aber manchmal zu verwirrend ist. Eine Überlagerung von Zuständen kann auch als die Tatsache betrachtet werden, dass ein Quantenobjekt zu jedem Zeitpunkt bestimmte Wahrscheinlichkeiten hat, in jede seiner Grenzstufen zusammenzufallen, und insgesamt sind diese Wahrscheinlichkeiten natürlich gleich 1 . Wenn wir das Qubit betrachten, werden wir uns diesbezüglich ausführlicher befassen.
Für Münzen ist dies visuell vorstellbar - abhängig von der Anfangsgeschwindigkeit, dem Wurfwinkel, dem Zustand der Umgebung, in der die Münze fliegt, und zu jedem Zeitpunkt ist die Wahrscheinlichkeit, einen „Adler“ oder „Schwanz“ zu bekommen, unterschiedlich. Und wie bereits erwähnt, kann man sich den Zustand einer solchen fliegenden Münze so vorstellen, dass sie sich „in allen ihren Grenzzuständen gleichzeitig befindet, aber mit einer anderen Wahrscheinlichkeit ihrer Umsetzung“.
Jedes Objekt, für das die obigen Eigenschaften erfüllt sind und das wir erstellen und verwalten können, kann als Speichermedium in einem Quantencomputer verwendet werden.
Ein wenig weiter werden wir über den aktuellen Stand der physikalischen Implementierung von Qubits als Quantenobjekte sprechen und darüber, was Wissenschaftler in dieser Eigenschaft jetzt verwenden.
Die dritte Eigenschaft besagt also, dass Quantenobjekte verschränkt werden können, um Quantensysteme zu erzeugen. Was ist ein Quantensystem?
Ein Quantensystem ist ein System verschränkter Quantenobjekte mit folgenden Eigenschaften:
- Ein Quantensystem überlagert alle möglichen Zustände der Objekte, aus denen es besteht
- Es ist unmöglich, den Zustand des Systems bis zum Zeitpunkt der Messung zu kennen
- Zum Zeitpunkt der Messung implementiert das System eine der möglichen Varianten seiner Grenzzustände
(und ein wenig voraus rennen)
Folgerung für Quantenprogramme :
- Ein Quantenprogramm hat einen bestimmten Zustand des Systems am Eingang, eine Überlagerung im Inneren und eine Überlagerung am Ausgang
- Bei der Programmausgabe nach der Messung haben wir eine probabilistische Implementierung eines der möglichen Endzustände des Systems (plus mögliche Fehler)
- Jedes Quantenprogramm hat eine Kaminarchitektur (Eingabe -> Ausgabe. Es gibt keine Zyklen, Sie können den Zustand des Systems in der Mitte des Prozesses nicht sehen.)
Vergleich eines Quantencomputers mit einem konventionellen
(zum Inhalt)

Vergleichen wir nun einen herkömmlichen Computer mit einem Quantencomputer.
Logikebene

Auf einem normalen Computer ist dies ein bisschen. Ein bekanntes deterministisches Stück durch und durch. Es kann Werte von 0 oder 1 annehmen. Es kommt gut mit der Rolle einer logischen Einheit für einen normalen Computer zurecht, ist jedoch zur Beschreibung des Zustands eines Quantenobjekts , das, wie wir bereits gesagt haben, mit der Annahme seiner Grenzzustände in der Luft liegt, völlig ungeeignet.
Dafür wurde ein Qubit erfunden. In seinen Randzuständen realisiert es die Zustände | 0> und | 1> ähnlich 0 und 1 und stellt in Überlagerung eine Wahrscheinlichkeitsverteilung über seine Randzustände |0> und |1> :
a|0> + b|1>, , a^2+b^2=1
in diesem Fall repräsentieren a und b die Amplituden der Wahrscheinlichkeiten und die Quadrate ihrer Module - die Wahrscheinlichkeiten selbst -, um genau solche Werte der Grenzzustände |0> und |1>, wenn das Qubit gerade durch Messung kollabiert.
Physische Ebene
Auf dem gegenwärtigen technologischen Entwicklungsstand ist die physikalische Implementierung eines Bits für einen regulären Computer ein Halbleitertransistor für ein Quantenobjekt, wie wir bereits gesagt haben. Im nächsten Abschnitt werden wir darüber sprechen, was jetzt als physikalischer Träger von Qubits verwendet wird.
Speichermedium
Für einen normalen Computer ist dies ein elektrischer Strom - Spannungspegel, Vorhandensein oder Nichtvorhandensein von Strom usw., für einen Quanten - genau der Zustand eines Quantenobjekts (Polarisationsrichtung, Spin usw.), der sich in einem Überlagerungszustand befinden kann.
Operationen
Um Logikschaltungen auf einem normalen Computer zu implementieren, verwenden wir alle bekannte logische Operationen , für Operationen mit Qubits mussten wir ein völlig anderes Operationssystem entwickeln, das als Quantentore bezeichnet wird . Die Gatter sind Single-Qubit und Two-Qubit, abhängig davon, wie viele Qubits konvertiert werden.
Beispiele für Quantentore:
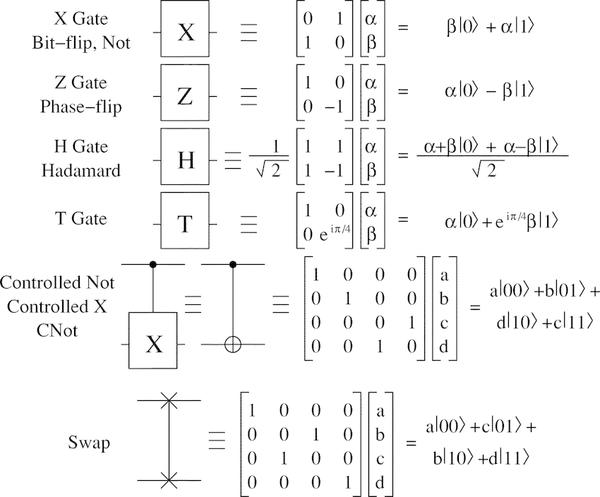
Es gibt das Konzept eines universellen Satzes von Gattern , die ausreichen, um eine Quantenberechnung durchzuführen. Ein universeller Satz umfasst beispielsweise ein Hadamard-Ventil, ein Phasenschieberventil, ein CNOT-Ventil und ein π⁄8-Ventil. Mit ihrer Hilfe können Sie eine beliebige Menge von Qubits einer Quantenberechnung unterziehen.
In diesem Artikel wird nicht näher auf das System der Quantentore eingegangen, sondern es werden zum Beispiel hier die logischen Operationen auf Qubits beschrieben. Die Hauptsache, an die Sie sich erinnern sollten:
- Operationen an Quantenobjekten erfordern die Erstellung neuer logischer Operatoren (Quantentore)
- Quantenventile sind Single-Qubit und Two-Qubit
- Es gibt universelle Sätze von Gattern, mit denen Sie eine beliebige Quantenberechnung durchführen können
Zusammenschaltung
Ein Transistor ist für uns völlig nutzlos, um Berechnungen anstellen zu können, müssen wir viele Transistoren miteinander verbinden, dh aus Millionen von Transistoren einen Halbleiterchip erstellen, auf dem wir bereits Logikschaltungen, ALUs und letztendlich einen modernen Prozessor in seiner klassischen Form erhalten.
Ein Qubit ist auch für uns völlig nutzlos (na ja, wenn auch nur in akademischer Hinsicht),
Für Berechnungen benötigen wir ein Qubitsystem (Quantenobjekte)
die, wie wir bereits gesagt haben, durch Verwickeln von Qubits untereinander entsteht, so dass Änderungen in ihren Zuständen gemeinsam auftreten.
Algorithmen
Die Standardalgorithmen, die die Menschheit bis zum heutigen Moment angesammelt hat, sind für die Implementierung auf einem Quantencomputer völlig ungeeignet. Ja, im Allgemeinen, und es besteht keine Notwendigkeit. Quantencomputer, die auf Gate-Logik über Qubits basieren, erfordern die Erstellung völlig anderer Algorithmen, Quantenalgorithmen. Von den bekanntesten Quantenalgorithmen können drei unterschieden werden:
Prinzip
Und der wichtigste Unterschied ist das Prinzip der Arbeit. Für einen Standardcomputer ist dies ein digitales, streng festgelegtes Prinzip , das auf der Tatsache basiert, dass, wenn wir einen Anfangszustand des Systems festlegen und einen bestimmten Algorithmus durchlaufen, das Ergebnis der Berechnungen das gleiche ist, unabhängig davon, wie oft wir diese Berechnung ausführen. Eigentlich ist dieses Verhalten genau das, was wir vom Computer erwarten.
Ein Quantencomputer arbeitet nach einem analogen, probabilistischen Prinzip . Das Ergebnis eines gegebenen Algorithmus in einem gegebenen Anfangszustand ist eine Stichprobe der Wahrscheinlichkeitsverteilung der endgültigen Implementierungen des Algorithmus plus möglicher Fehler.
Diese wahrscheinlichkeitstheoretische Natur des Quantencomputers beruht auf dem sehr wahrscheinlichkeitstheoretischen Wesen der Quantenwelt. "Gott würfelt nicht mit dem Universum ", sagte der alte Einstein, aber alle bisherigen Experimente und Beobachtungen (im aktuellen wissenschaftlichen Paradigma) bestätigen das Gegenteil.
Physikalische Implementierungen von Qubits
(zum Inhalt)

Wie wir bereits gesagt haben, kann ein Qubit durch ein Quantenobjekt dargestellt werden, dh ein solches physikalisches Objekt, das die oben beschriebenen Quanteneigenschaften implementiert. Das heißt, grob gesagt, jedes physikalische Objekt, in dem zwei Zustände vorliegen und diese beiden Zustände sich in einem Überlagerungszustand befinden, kann zum Aufbau eines Quantencomputers verwendet werden.
„Wenn wir ein Atom auf zwei verschiedenen Ebenen platzieren und kontrollieren können, dann ist hier ein Qubit für Sie. Wenn wir das mit einem Ion machen können, Qubit. Das Gleiche gilt für Strom. Wenn wir es gleichzeitig im und gegen den Uhrzeigersinn laufen lassen, ist hier ein Qubit. “ (C)
Es gibt einen wunderbaren Kommentar zu dem Artikel, in dem die aktuelle Vielfalt der physikalischen Realisierungen des Qubits genauer betrachtet wird, aber wir listen nur die bekanntesten und gebräuchlichsten auf:
Von all dieser Vielfalt ist das erste Verfahren zur Herstellung von Qubits auf der Basis von Supraleitern das am besten ausgearbeitete. Google , IBM , Intel und andere führende Player verwenden es, um ihre Systeme zu erstellen.
Lesen Sie auch die Übersicht über mögliche physikalische Realisierungen von Qubits aus Andrew Daley, 2014 .
Die Grundlagen. Das Funktionsprinzip eines Quantencomputers
(zum Inhalt)

Die Materialien für diesen Abschnitt (Aufgabe und Bilder) stammen aus dem Artikel „Just about the complex. Wie ein Quantencomputer funktioniert . “
Stellen wir uns also vor, wir haben folgende Aufgabe:
Es gibt eine Gruppe von drei Personen: (A) Ndrey, (B) Olodya und (C) Häresie . Es gibt zwei Taxis (0 und 1) .
Es ist auch bekannt, dass:
- (A) ndrey, (B) olodya - Freunde
- (A) ndrey, (C) Ketzerei - Feinde
- (B) Olodya und (C) Häresie - Feinde
Aufgabe: Leute mit dem Taxi so platzieren, dass Max (Freunde) und Min (Feinde)
Punktzahl: L = (Anzahl der Freunde) - (Anzahl der Feinde) für jede Unterkunftsoption
WICHTIG: Angenommen, es gibt keine Heuristik und keine optimale Lösung. In diesem Fall wird das Problem nur durch eine umfassende Suche nach Optionen gelöst.
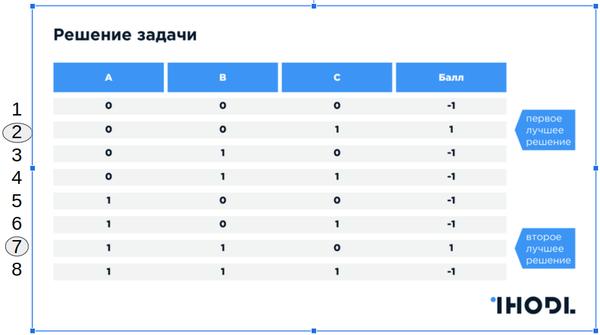
Lösung auf einem normalen Computer
Wie man dieses Problem auf einem normalen (Super-) Computer (oder Cluster) löst - es ist klar, dass wir alle möglichen Optionen in einer Schleife sortieren müssen . Wenn wir ein Multiprozessorsystem haben, können wir die Berechnung von Lösungen auf mehreren Prozessoren parallelisieren und die Ergebnisse dann sammeln.
Wir haben 2 mögliche Unterkunftsmöglichkeiten (Taxi 0 und Taxi 1) und 3 Personen. Der Lösungsraum ist 2 ^ 3 = 8 . Sie können sogar mit einem Taschenrechner 8 Optionen durchgehen, dies ist kein Problem. Und jetzt werden wir die Aufgabe komplizieren - wir haben 20 Leute und zwei Busse, der Lösungsraum ist 2 ^ 20 = 1.048.576 . Nichts zu kompliziert. Erhöhen wir die Anzahl der Personen um das 2,5-fache - nehmen wir 50 Personen und zwei Züge, der Entscheidungsraum ist jetzt 2 ^ 50 = 1,12 x 10 ^ 15 . Ein normaler (Super-) Computer hat bereits ernsthafte Probleme. Wir erhöhen die Anzahl der Personen um das 2-fache. 100 Personen geben uns 1,2 x 10 ^ 30 mögliche Optionen.
Alles, was in einer angemessenen Zeit, kann diese Aufgabe nicht gezählt werden.
Wir verbinden einen Supercomputer
Der derzeit leistungsstärkste Computer ist die Nummer 1 der Top500 , es handelt sich um Summit mit einer Kapazität von 122 Pflops . Nehmen wir an, dass für die Berechnung einer Option 100 Operationen ausreichen, um das Problem für 100 Personen zu lösen:
(1,2 × 10 30 100) / 122 × 10 15 / (60 60 24 365) = 3 × 10 37 Jahre.
Wie wir sehen, wächst der Lösungsraum mit zunehmender Dimension der Quellendaten gemäß einem Potenzgesetz . Im allgemeinen Fall für N Bits haben wir 2 ^ N mögliche Lösungen, die uns mit relativ kleinem N (100) einen unlesbaren (auf dem gegenwärtigen technologischen Niveau) Raum geben Entscheidungen.
Gibt es Alternativen? Wie Sie vielleicht erraten haben, gibt es das.
Bevor wir uns jedoch damit befassen, wie und warum Quantencomputer solche Probleme effektiv lösen können, wollen wir uns ein wenig daran erinnern, was eine Wahrscheinlichkeitsverteilung ist . Seien Sie nicht beunruhigt, der Übersichtsartikel, es wird hier keine harte Mathematik geben, wir werden mit einem klassischen Beispiel mit Tasche und Bällen auskommen.
Ein bisschen Kombinatorik, Wahrscheinlichkeitstheorie und ein seltsamer Experimentator
Nehmen Sie eine Tüte und legen Sie 1000 weiße und 1000 schwarze Kugeln hinein . Wir werden ein Experiment durchführen - nimm den Ball heraus, schreibe die Farbe auf, lege den Ball wieder in den Beutel und mische die Kugeln im Beutel.
Wir haben das Experiment 10 Mal durchgeführt und 10 schwarze Kugeln herausgezogen . Vielleicht? Ganz. Gibt uns dieses Beispiel ein vernünftiges Konzept für die tatsächliche Verteilung im Beutel? Offensichtlich nicht. Was Sie tun müssen, ist richtig, wiederholen Sie das Experiment eine Million Mal und berechnen Sie die Häufigkeit des Falls von schwarzen und weißen Kugeln. Wir erhalten zum Beispiel 49,95% Schwarz und 50,05% Weiß . In diesem Fall ist die Verteilungsstruktur, von der wir abtasten, bereits mehr oder weniger klar (wir nehmen eine Kugel).
Das Wichtigste, was Sie verstehen müssen, ist, dass das Experiment selbst probabilistischer Natur ist. Bei einer Probe (Kugel) erkennen wir die wahre Verteilungsstruktur nicht. Wir müssen das Experiment viele Male wiederholen und die Ergebnisse mitteln.
Füge 10 rote und 10 grüne Kugeln in unsere Tasche ein (Fehler). Wiederholen Sie den Versuch 10 Mal. In gezogen 5 rot und 5 grün . Vielleicht? Ja Wir können etwas über die wahre Verbreitung sagen - Nein. Was zu tun ist - verstehen Sie?
Um die Struktur der Wahrscheinlichkeitsverteilung zu verstehen, müssen einzelne Ergebnisse aus dieser Verteilung wiederholt abgetastet und die Ergebnisse gemittelt werden.
Wir verbinden Theorie mit Praxis
Anstelle von schwarzen und weißen Bällen nehmen wir jetzt die Billardkugeln und legen 1000 Bälle mit der Nummer 2, 1000 mit der Nummer 7 und 10 Bälle mit anderen Nummern in den Beutel. Stellen Sie sich einen Experimentator vor, der in einfachen Schritten geschult ist (Ball holen, Nummer notieren, Ball zurück in den Beutel legen, Bälle in den Beutel mischen) und das in 150 Mikrosekunden. Na ja, so ein Experimentator über Hilfsmittel (keine Drogenwerbung !!!). Dann wird er in 150 Sekunden in der Lage sein, unser Experiment 1 Million Mal durchzuführen und uns die Ergebnisse der Mittelwertbildung zu liefern.
Sie setzten den Experimentator ab, gaben den Beutel ab, wandten sich ab, warteten 150 Sekunden - erhielten:
Nummer 2 - 49,5%, Nummer 7 - 49,5%, die restlichen Zahlen in der Menge - 1%.
Ja, das stimmt, unsere Tasche ist ein Quantencomputer mit einem Algorithmus, der unser Problem löst , und Kugeln sind mögliche Lösungen. Da es zwei richtige Lösungen gibt, gibt uns ein Quantencomputer mit gleicher Wahrscheinlichkeit eine dieser möglichen Lösungen und 0,5% (10/2000) Fehler , über die wir später sprechen werden.
Um das Ergebnis eines Quantencomputers zu erhalten, müssen Sie den Quantenalgorithmus wiederholt mit demselben Eingabedatensatz ausführen und das Ergebnis mitteln.
Skalierbarkeit eines Quantencomputers
Stellen wir uns nun vor, dass es für ein Problem, an dem 100 Personen beteiligt sind (wir erinnern uns an diesen Entscheidungsraum 2 ^ 100 ), nur zwei richtige Lösungen gibt. Wenn wir dann 100 Qubits nehmen und einen Algorithmus schreiben, der unsere Zielfunktion (L, siehe oben) über diese Qubits berechnet, erhalten wir einen Beutel mit 1000 Bällen mit der Nummer der ersten richtigen Antwort, 1000 mit der Nummer der zweiten richtigen Antwort und 10 Bällen mit anderen Nummern. Und unser Experimentator wird uns in den gleichen 150 Sekunden eine Schätzung der Wahrscheinlichkeitsverteilung der richtigen Antworten geben .
Die Ausführungszeit des Quantenalgorithmus (mit einigen Annahmen) kann als konstant O (1) in Bezug auf die Dimension des Lösungsraums (2 ^ N) angesehen werden.
Und genau diese Eigenschaft eines Quantencomputers - die Konstanz der Ausführungszeit in Bezug auf die Komplexität des nach dem Potenzgesetz wachsenden Entscheidungsraums ist der Schlüssel.
Qubit und Parallelwelten
Wie kommt das zustande? Wie kann ein Quantencomputer so schnell rechnen? Es geht um die Quantennatur von Qubit.
Schauen Sie, wir sagten, dass ein Qubit als Quantenobjekt einen seiner zwei Zustände realisiert, wenn es beobachtet wird , aber in der „lebenden Natur“ befindet es sich in einer Überlagerung von Zuständen , dh es befindet sich gleichzeitig (mit einer gewissen Wahrscheinlichkeit) in beiden Grenzzuständen.
Nehmen Sie (A) Ndrey und stellen Sie sich seinen Zustand (in dem das Fahrzeug 0 oder 1 ist) als Qubit vor. Dann haben wir (in einem Quantenraum) zwei parallele Welten , in einer (A) sitzen in einem Taxi 0, in einer anderen Welt - in einem Taxi 1. Zur gleichen Zeit in zwei Taxis , aber mit einer gewissen Chance, es in jedem von ihnen zu finden, wenn wir beobachten.
Nehmen Sie (B) olod und stellen Sie sich auch seinen Zustand als Qubit vor. Es entstehen zwei weitere Parallelwelten. Aber während diese Weltenpaare (A) und (B) in keiner Weise interagieren. Was muss getan werden, um ein verbundenes System zu erstellen? Das ist richtig, Sie müssen diese Qubits verbinden (verwirren) . Wir nehmen und verwechseln (A) mit (B) - wir erhalten ein Quantensystem aus zwei Qubits (A, B), das in sich vier voneinander abhängige Parallelwelten implementiert. Addiere (C) erge und erhalte ein System von drei Qubits (ABC), das acht voneinander abhängige parallele Welten implementiert.
Die Essenz des Quantenrechnens (die Implementierung einer Kette von Quantentoren über ein System von gekoppelten Qubits) ist die Tatsache, dass die Berechnung in allen parallelen Welten gleichzeitig stattfindet.
Und egal wie viele von ihnen wir haben, 2 ^ 3 oder 2 ^ 100, der Quantenalgorithmus wird in einer endlichen Zeit über all diese parallelen Welten ausgeführt und gibt uns das Ergebnis, das eine Stichprobe aus der Wahrscheinlichkeitsverteilung der Antworten des Algorithmus ist.
Zum besseren Verständnis können wir uns vorstellen, dass ein Quantencomputer auf Quantenebene 2 ^ N parallele Entscheidungsprozesse startet , von denen jeder eine mögliche Option bearbeitet , dann die Arbeitsergebnisse sammelt - und uns die Antwort in Form einer Überlagerung der Lösung (Wahrscheinlichkeitsverteilung der Antworten) aus die wir jedes Mal (in jedem Experiment) einmal abtasten.
Denken Sie an die Zeit, die unser Experimentator benötigt (150 μs) , um das Experiment durchzuführen. Dies wird sich etwas weiter als nützlich erweisen, wenn wir über die Hauptprobleme von Quantencomputern und die Dekohärenzzeit sprechen.
Quantenalgorithmen
(zum Inhalt)
Wie bereits erwähnt, sind herkömmliche Algorithmen, die auf binärer Logik basieren, nicht auf einen Quantencomputer anwendbar, der Quantenlogik (Quantentore) verwendet. Für ihn musste er neue entwickeln, die das Potenzial der Quantennatur des Computing voll ausschöpfen.
Die bekanntesten Algorithmen sind heute:
Im Gegensatz zu klassischen sind Quantencomputer nicht universell.
Bisher wurden nur wenige Quantenalgorithmen gefunden. (C)
Dank Oxoron für den Link zum Quantum Algorithm Zoo , dem Ort, an dem sich nach Angaben des Autors ( Stephen Jordan ) die besten Vertreter der Welt der Quantenalgorithmen versammelt haben und weiterhin versammeln.
In diesem Artikel werden wir Quantenalgorithmen nicht im Detail analysieren, es gibt viele hervorragende Materialien im Web für jede Komplexitätsebene, aber Sie müssen noch kurz die drei bekanntesten behandeln.
Shore-Algorithmus.
(zum Inhalt)
Der bekannteste Quantenalgorithmus ist der Shor-Algorithmus (1994 vom englischen Mathematiker Peter Shor erfunden), mit dem das Problem der Zerlegung von Zahlen in Primfaktoren (Faktorisierungsproblem, diskreter Logarithmus) gelöst werden soll.
Dieser Algorithmus wird als Beispiel verwendet, wenn darauf hingewiesen wird, dass Ihre Banksysteme und Kennwörter bald gehackt werden. Wenn man bedenkt, dass die Länge der heute verwendeten Schlüssel nicht weniger als 2048 Bit beträgt, ist die Zeit für die Obergrenze noch nicht gekommen.
Bisher sind die Ergebnisse mehr als bescheiden. Die besten Faktorisierungsergebnisse unter Verwendung des Shore-Algorithmus sind die Nummern 15 und 21 , was viel weniger als 2048 Bit ist. Für die übrigen Ergebnisse aus der Tabelle wurde ein anderer Berechnungsalgorithmus verwendet, aber selbst das beste Ergebnis gemäß diesem Algorithmus (291311) ist weit von der tatsächlichen Anwendung entfernt.
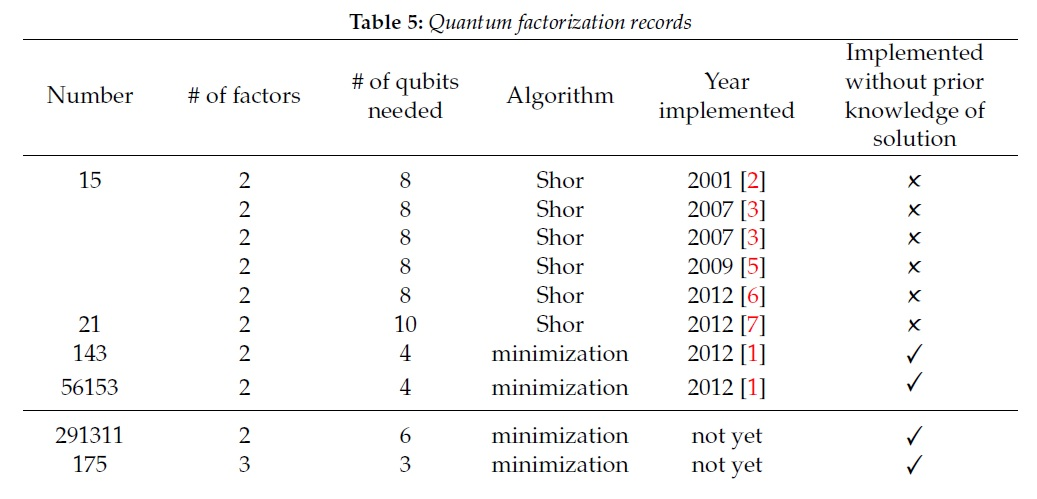
Hier können Sie beispielsweise mehr über den Shore-Algorithmus lesen. Über die praktische Umsetzung - hier .
Eine der aktuellen Schätzungen zur Komplexität und Leistung, die zur Faktorisierung einer 2048-Bit-Zahl erforderlich ist, ist ein Computer mit 20 Millionen Qubits . Wir schlafen friedlich.
Grover-Algorithmus
(zum Inhalt)
Der Algorithmus von Grover ist ein Quantenalgorithmus zur Lösung des Aufzählungsproblems, dh zur Lösung der Gleichung F(X) = 1 , wobei F eine Boolesche Funktion von n Variablen ist. Es wurde 1996 vom amerikanischen Mathematiker Lov Grover vorgeschlagen.
Der Algorithmus von Grover kann verwendet werden, um den Median und das arithmetische Mittel einer Zahlenreihe zu ermitteln. Darüber hinaus können damit NP-vollständige Probleme gelöst werden, indem unter den vielen möglichen Lösungen eine umfassende Suche durchgeführt wird. Dies kann zu einer signifikanten Geschwindigkeitssteigerung im Vergleich zu klassischen Algorithmen führen, ohne jedoch generell eine „ Polynomlösung “ bereitzustellen . (C)
Sie können hier oder hier mehr lesen. Es gibt auch eine gute Erklärung des Algorithmus am Beispiel der Kisten und des Balls, aber aus Gründen, die sich meiner Kontrolle entziehen, öffnet sich diese Seite für mich aus Russland nicht. Wenn Ihre Website auch blockiert ist, ist hier eine kurze Zusammenfassung:
Grovers Algorithmus. Stellen Sie sich vor, Sie haben N nummerierte geschlossene Kästchen. Sie sind alle leer, bis auf den, in dem sich der Ball befindet. Ihre Aufgabe: Herausfinden der Nummer des Kastens, in dem sich der Ball befindet (diese unbekannte Nummer wird häufig mit dem Buchstaben w bezeichnet).

Wie kann man dieses Problem lösen? Öffnen Sie abwechselnd die Kisten, und früher oder später werden Sie auf eine Kiste mit einer Kugel stoßen. , ? N/2. , 100 , 100 , , .
. , , (Oracle). — « 732», « 732 ». , , « , »
, , , : N SQRT(N) !
.
-
( )
— ( — ) — [ ]( https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%BE%D0%B2%D1%8B%D0%B9 %D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC), 1992 , , . _
— , F(x1, x2, … xn) ( 0, 1 ) ( 0, 1). , , . ()
. :
( — ) , . , . : «» «» – , «», «» — . , , – . ()
( )

, . ( ) :
“ ”, .
:
( )
N+1 .
, , ( ) . , , — .
, (-273.14 ) - , () .
, , .
.
, . — IBM IBM Q System One Google Sycamore . , (2) 200 .
Sycamore, — 1 200 , — 130 . 150 . ? .
?
, 150 N — .
:
150 . — .
...
Fehler
( )

, , 100% , - . , . :
, , , . , , . , , , .
— () , , , . — “ ?” — 5050, .
, ( ) - . . N 1 .
— . , 100 , 80 , 20.
— , . .
. , — IBM IBM Q System One Google Sycamore :
— . 1-Fidelity. , 2- .
2016 NQIT .
( )

, . () , , .
1- , , 12-, , , . , , , , .
, , , “ ” “” . .
:
, , . , , . - , .
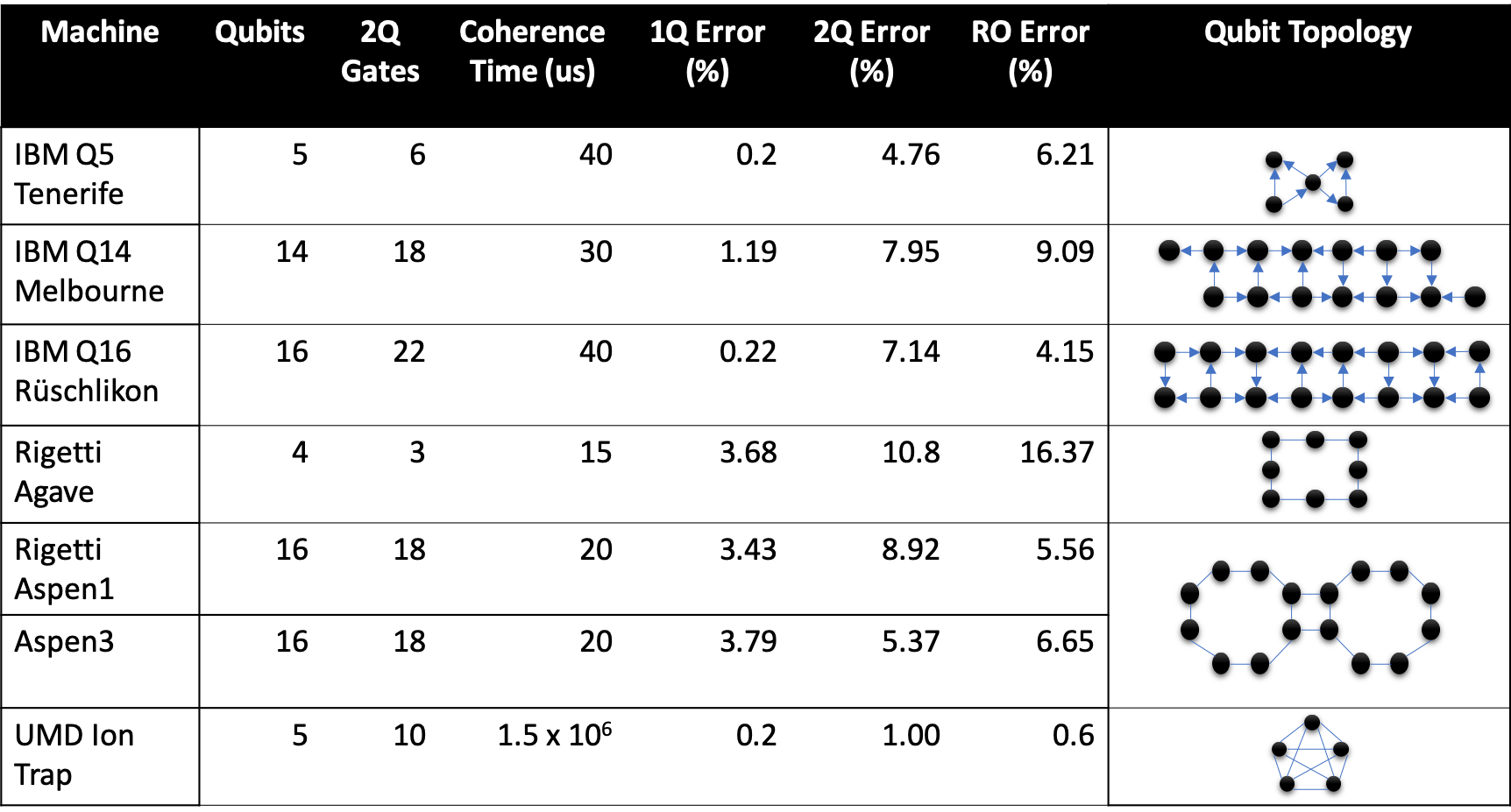
Also:
Zusammenfassung
( )
— . 150 :
, 0.5 , :
We measure a qubit coherence time in excess of 0.5 s, and with magnetic shielding we expect this to improve to be longer than 1000 s
, , .
, , , .
, , , 1 4 1 6.
( )
, :
, , ( ) , . ( ), , .
D-Wave
( )

2000- D-Wave 2000Q. : D-Wave Systems
Google 53- , D-Wave, , . , 53 , 2048 ? ...
( ):
D-Wave ( ), , .
, , , (, ), Scott Aaronson . , ,
D-Wave. , 2014 IBM , D-Wave . , 2015 Google NASA , , , . Google , , .
, D-Wave, . , . , — . , D-Wave ASIC .
( )
. , :
- , 232 264 (8-16 )
- N 2^N , .. 2^(3+N) 32- 2^(4+N) 64- .
- N 2^N x 2^N
:
()
, Summit ( Top-1 Top-500 ) 2.8 .
— 49 ( Sunway Taihu Light )
.
. :
— 49 - 39 "" ( ) 2^63 — 4 4
50+ . - Google 53- .
.
( )

:
́ ́ — , .
, , , , , . .
, “ ”. , 50+ , , , . .
, . , Google, Sycamore .
Google
( )

54- Sycamore
, 2019 Google Nature « ». 54- «Sycamore».
Sycamore 54- , 53-. , , 54- , . , 53- .
, .
IBM , Google . , 2,5 , , . .
, , Scott Aaronson . Scott's Supreme Quantum Supremacy FAQ! , . FAQ, , , .
Google? , :
, , , . : (.. 1- 2- — — , 20, 2D n=50-60 ). , 0, {0,1}, n- () . , , .
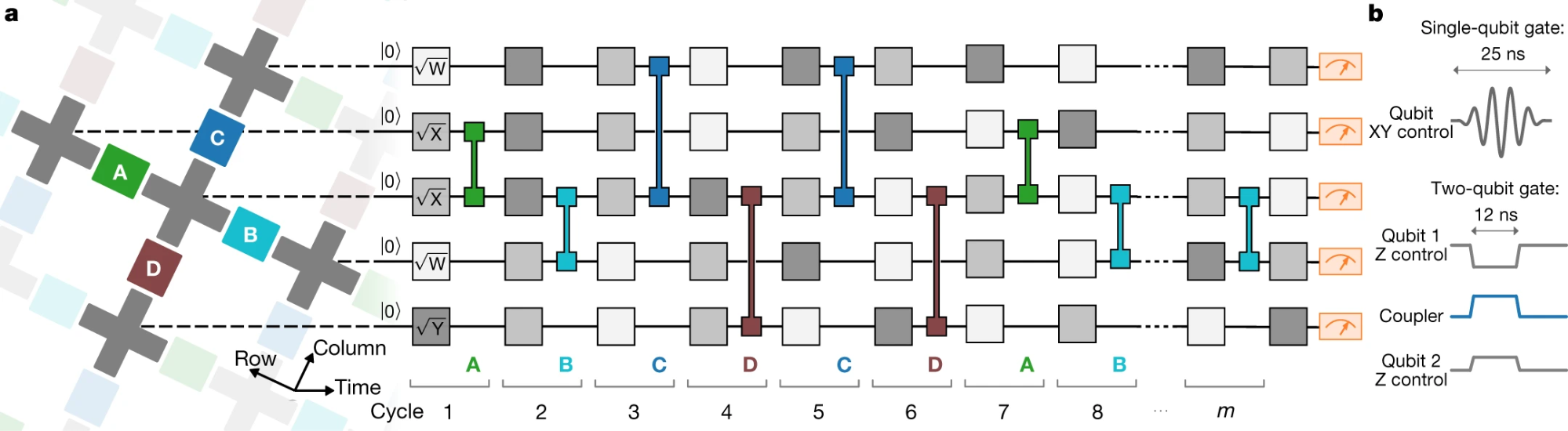
:
Google 53- , .
— Google , , , , , . , 2048- .
Zusammenfassung
( )

— , .
(-) :
:
:
:
( ), , - , .
— , , . .
Fazit
( )
, , , , D-Wave Google .
(, , ..) , , , , .. , .
, - .
() Kruegger
Danksagung
( )

@Oxoron , “ ”
@a5b - “ ” , , .
, .
( )

[The National Academies Press]