Das Studium der Neutrinos führte zu einer unerwarteten Entdeckung in der Mathematik

Drei Physiker wollten den Prozess der Veränderung von Neutrinos berechnen. Als Ergebnis fanden sie eine unerwartete Beziehung zwischen einigen der häufigsten Objekte der Mathematik.

Eines Tages im August, am Morgen nach dem Frühstück, öffnete der Mathematiker Terence Tao eine E-Mail von drei Physikern, mit denen er nicht vertraut war. Trinity erklärte ihm, dass sie über eine einfache Formel gestolpert sei, die, falls zutreffend, eine unerwartete Beziehung zwischen einigen der grundlegendsten und wichtigsten Objekte der linearen Algebra beschreiben würde.

Die Formel "sah zu gut aus, um wahr zu sein", sagte Tao, Professor an der University of California in Los Angeles, ein Fields-Gewinner , einer der weltweit führenden Mathematiker. "Etwas so Kurzes und Einfaches hätte schon vor langer Zeit in Lehrbüchern stehen müssen", sagte er. "Deshalb dachte ich zuerst - nein, das kann nicht sein."

Und dann dachte er ein bisschen mehr nach.

Physiker - Stephen Park vom National Accelerator Laboratory. Fermi, Xining Zhang von der University of Chicago und Peter Denton vom Brookhaven National Laboratory haben sich vor zwei Monaten diese mathematische Identität zugelegt, um mit dem seltsamen Verhalten von Elementarteilchen, den sogenannten Neutrinos , umzugehen.

Sie stellten fest, dass schwer zu berechnende „ Eigenvektoren “, die in ihrem Fall beschreiben, wie sich Neutrinos in Materie ausbreiten, einer Kombination von Begriffen gleichgesetzt werden, die als „Eigenwerte“ bezeichnet werden und viel einfacher zu berechnen sind. Darüber hinaus stellten sie fest, dass diese Beziehung zwischen Eigenvektoren und Eigenwerten - sehr häufig in mathematischen, physikalischen und technischen Berechnungsobjekten, die seit dem 18. Jahrhundert untersucht wurden - allgemeiner zu sein scheint.

Obwohl die Physiker nicht glauben konnten, dass sie eine neue Tatsache im Zusammenhang mit einer solchen Grundmathematik entdeckt hatten, konnten sie weder in Büchern noch in Artikeln eine solche Beziehung finden. Deshalb beschlossen sie, ein Risiko einzugehen und sich mit Tao in Verbindung zu setzen, obwohl auf seiner Website die Bitte lautete, ihn in solchen Fällen nicht zu stören.

"Zu unserer Überraschung antwortete er zwei Stunden später und sagte, dass er so etwas noch nie zuvor gesehen hatte", sagte Park. Und außerdem gab es in Taos Antwort drei unabhängige Beweise für diese Identität.


Xining Zhang, Peter Denton und Stephen Park mit offener Formel

Eineinhalb Wochen später veröffentlichten die Physiker und Tao, die Park den „Feuerlöschschlauch der Mathematik“ nennt, einen Artikel im Internet, in dem über eine neue Formel berichtet wurde. Jetzt wird diese Arbeit von Fachleuten der Zeitschrift Communications in Mathematical Physics evaluiert. In einem separaten Artikel, der im Journal of High Energy Physics veröffentlicht wurde, verwenden Denton, Park und Zhang diese Formel, um Gleichungen zu vereinfachen, die das Verhalten von Neutrinos beschreiben.

Experten sagen, dass diese Formel möglicherweise mehr Anwendungsmöglichkeiten bietet, da bei einer Vielzahl von Aufgaben die Berechnung von Eigenvektoren und Eigenwerten erforderlich ist. "Es hat eine breite Palette von Anwendungen", sagte John Bickom , ein Spezialist für Teilchenphysik an der Ohio University. "Wer weiß, welche Türen sie öffnen kann."

Mathematiker denken genauso. "Das ist sowohl überraschend als auch interessant", sagte Van Wu , Mathematiker an der Yale University. "Ich ahnte nicht, dass es möglich war, Eigenvektoren nur mit Informationen über Eigenwerte zu berechnen."

Vu und Tao zeigten 2009 eine ähnliche Identität (weshalb Denton, Park und Zhang beschlossen, sich mit Tao in Verbindung zu setzen), die neue Formel folgt jedoch offensichtlich nicht der alten. Und obwohl eine ähnliche Formel zufällig im Mai dieses Jahres in einer mathematischen Arbeit auftauchte, haben ihre Autoren sie nicht mit Eigenvektoren und Eigenwerten assoziiert.

In gewisser Weise ist es nicht verwunderlich, dass eine neue Idee über mehrere Jahrhunderte alte mathematische Objekte von Physikern stammt. Die Natur hat die mathematische Forschung inspiriert, seit Menschen begannen, mit 10 Fingern zu rechnen. "Damit Mathematik gedeihen kann, muss sie mit der Natur verbunden sein", sagte Vu. "Es gibt keinen anderen Weg."

Transformationstricks

Eigenvektoren und Eigenwerte sind so häufig, weil sie lineare Transformationen charakterisieren: Operationen, die alle Teile desselben Objekts gleichermaßen dehnen, komprimieren, drehen oder auf andere Weise ändern. Diese Transformationen werden durch rechteckige Anordnungen von Zahlen dargestellt, die Matrizen genannt werden. Eine Matrix dreht das Objekt um 90 Grad. der andere dreht es um und halbiert es.


Wenn Sie diese Matrix auf ein bestimmtes Objekt anwenden, wird sie relativ zur Ebene gespiegelt und ihre Höhe verdoppelt. Die Eigenvektoren der Matrix beschreiben die Richtungen, in denen sich das Objekt außer bei der Skalierung nicht ändert. Die Eigenwerte der Matrix beschreiben, um wie viel das Objekt entlang dieser Eigenvektoren skaliert.
Der Eigenvektor A verläuft parallel zur vertikalen Achse. Sein Eigenwert ist 2, weil das Objekt seine Höhe verdoppelt.
Der Eigenvektor B liegt in der Reflexionsebene. Sein Eigenwert ist 1, da sich das Objekt nicht ändert.
Der Eigenvektor C ist senkrecht zur Reflexionsebene. Sein Eigenwert ist -1, was Reflexion relativ zur Ebene bedeutet.
Durch Löschen von Zeilen und Spalten einer Matrix können kleinere Matrizen erstellt werden. Ihre Eigenwerte können zusammen mit den Eigenwerten der ursprünglichen Matrizen verwendet werden, um die Eigenvektoren der ursprünglichen Matrizen zu berechnen.

Die Matrizen ändern dazu die „Vektoren“ der Objekte - mathematische Pfeile, die auf jeden physischen Ort des Objekts zeigen. Die Eigenvektoren einer Matrix sind diejenigen Vektoren, die nach dem Aufbringen der Matrix weiterhin in dieselbe Richtung weisen wie zuvor. Angenommen, wir nehmen eine Matrix, die ein Objekt um 90 Grad um die x-Achse dreht: Die Eigenvektoren sind entlang der x-Achse ausgerichtet, da sich die auf dieser Achse befindlichen Punkte nicht drehen, wenn sich alle anderen um sie drehen.

Eine ähnliche Matrix kann Objekte um die x-Achse drehen und zweimal komprimieren. Um wie viel die Matrix die Eigenvektoren des Objekts komprimiert oder dehnt, beschreiben die entsprechenden Eigenwerte - in diesem Fall 1/2 (wenn sich der Eigenvektor nicht ändert, ist sein Eigenwert 1).


Terence Tao

Die Eigenvektoren und Eigenwerte sind unabhängig und müssen normalerweise separat berechnet werden, beginnend mit den Zeilen und Spalten der Matrix. Die Schüler lernen dies für einfache Matrizen. Die neue Formel unterscheidet sich jedoch von den vorhandenen Methoden. "Das Interessante an dieser Identität ist, dass Sie keine in der Matrix enthaltenen Werte kennen müssen, um etwas zu berechnen", sagte Tao.

Die Identität wird auf hermitische Matrizen angewendet, die reale Transformationen von Eigenvektoren (im Gegensatz zu imaginären Zahlen) ausführen, und gilt daher für Situationen, die in der Realität auftreten. Die Formel drückt jeden Eigenvektor der Hermitianischen Matrix durch die Eigenwerte dieser Matrix und ihrer „Nebenmatrix“ aus - eine solche kleinere Matrix, die durch Löschen der Zeile und Spalte aus dem Original erhalten wird.

Rückblickend erscheint die Formel vernünftig, sagte Tao, da die Eigenwerte der Nebenmatrix verborgene Informationen in sich selbst kodieren. "Ich persönlich hätte zum Beispiel nie an so etwas gedacht."

Er sagte, dass ein Werkzeug, das nichts mit einer Aufgabe zu tun habe, in der Mathematik selten vorkomme. Er glaubt jedoch, dass die Verbindung von Eigenvektoren und Eigenwerten eine Rolle spielen muss. "Es ist so schön, dass ich mir sicher bin, dass die Formel in naher Zukunft Anwendung finden wird", sagte er. "Bisher haben wir nur eine Verwendung für sie."

Werwolfpartikel

Und diese Anwendung ist mit Neutrinos verbunden: die seltsamste, am wenigsten untersuchte und geheimnisvollste der bekannten fundamentalen Teilchen. Jede Sekunde passieren Billionen solcher Partikel den menschlichen Körper, aber da sie praktisch nicht vorhanden sind, bleiben viele ihrer Eigenschaften unbekannt.

Interessanterweise behauptet die Theorie, dass genau die Unterschiede im Verhalten von Neutrinos und Antineutrinos dazu führen können, dass Materie im Universum die Antimaterie dominiert . Wenn die beiden Gegensätze nach dem Urknall in gleichen Mengen auftauchten, würden sie sich gegenseitig auslöschen, und im Weltraum würde nichts außer Licht übrig bleiben. Der Unterschied zwischen einem Neutrino und einem Antineutrino könnte zu einem lebenswichtigen Überschuss an Materie führen. "Wenn sie sich anders verhalten, können wir uns vorstellen, warum das Universum mit Materie gefüllt ist", sagte Deborah Harris , Physikerin an der York University und Fermilab, die am DUNE- Experiment (Deep Underground Neutrino Experiment, ein tief unterirdisches Neutrino) arbeitete Experiment) entwickelt, um solche Unterschiede zu messen.

Das Experiment, bei dem die Eigenschaften von Neutrinos gemessen werden, die von Fermilab in Illinois zu einem unterirdischen Detektor in 1300 km Entfernung von der Quelle in South Dakota gebracht wurden, basiert auf der Tatsache, dass es drei verschiedene Arten von Neutrinos gibt - Elektron, Myon und Tau. Jeder Typ ist jedoch eine quantenmechanische Mischung, und Neutrinos oszillieren und ändern unterwegs ihren Typ. Wenn sich Neutrinos von Fermilab fortbewegen, ändert sich ihre Mischung, so dass sich das Myon-Neutrino in ein Elektron oder ein Tau-Neutrino verwandeln kann.

Diese Schwingungen werden durch eine äußerst komplexe 3x3-Matrix beschrieben. Basierend auf den Eigenvektoren und -werten können Physiker einen Ausdruck berechnen, der die Wahrscheinlichkeit beschreibt, dass ein Myon-Neutrino zum Zeitpunkt seiner Ankunft in South Dakota in ein elektronisches Neutrino umgewandelt wird. Sie berechnen auch die Wahrscheinlichkeit, dass ein Myon-Neutrino ein Elektron-Antineutrino wird.


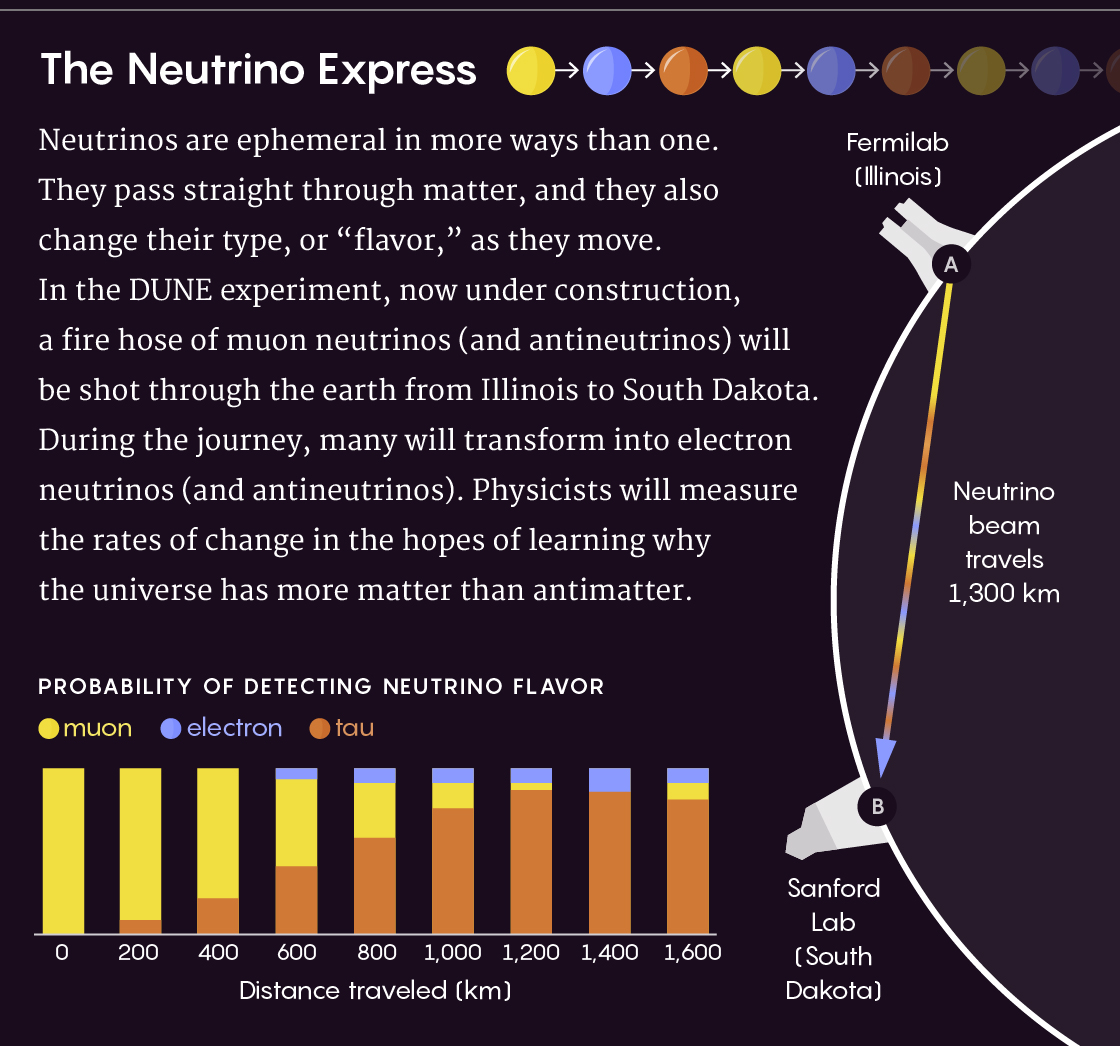Die kurzlebigen Teilchen eines Neutrinos passieren nicht nur die Materie, sondern ändern auch ihren Typ im Flug. Im DUNE-Experiment wird ein Neutrino-Strahl gestartet, von dem viele auf dem Weg von der Quelle zum Ziel ihren Typ ändern. Diese Veränderungen werden von Physikern gemessen.
Das Diagramm zeigt die Wahrscheinlichkeit des Nachweises von Neutrinos verschiedener Arten in Abhängigkeit von ihrer Reichweite in km. Gelb - Myon, Blau - Elektronisch, Braun - Tau.

Diese Ausdrücke enthalten das Unbekannte: die „Phase der Verletzung der CP-Invarianz “, die zeigt, wie sich die Gesetze der Neutrino- und Antineutrino-Oszillationen voneinander unterscheiden. Wissenschaftler mit DUNE können dieses Unbekannte durch Messen und Vergleichen der realen Schwingungsverhältnisse berechnen. Wenn die Störungsphase groß genug ist, erklärt dies, warum das Universum mit Materie gefüllt ist.

Und als ob diese Schwierigkeiten nicht genug wären, macht ein seltsamer Effekt, dessen Voraussetzungen 1978 von dem Physiker Lincoln Wolfenstein entdeckt wurden, die Neutrinomatrix noch komplexer. Neutrinos interagieren selten mit Materie im üblichen Sinne, aber Wolfenstein stellte fest, dass ihr Durchgang durch Materie im Gegensatz zum leeren Raum immer noch die Art und Weise verändert, wie sie sich fortpflanzen. Manchmal interagiert ein durch Materie dringendes Neutrino mit den Elektronen in einem Atom und ändert damit im Wesentlichen die Orte: Ein Elektronenneutrino verwandelt sich in ein Elektron und umgekehrt.

Solche Substitutionen führen einen neuen Begriff in die Matrix ein, der sich auf Elektronenneutrinos auswirkt, was die Mathematik erheblich kompliziert. Es ist dieser Effekt von Mikheev - Smirnov - Wolfenstein [der 1985 von den sowjetischen Physikern Stanislav Mikheev und Alexey Smirnov anhand des Falls von Neutrinoschwingungen in einem Medium mit konstanter Dichte vorhergesagt und theoretisch untersucht wurde], der Park, Zhang und Denton dazu veranlasste, einen Weg zu finden, die Berechnung zu vereinfachen .

Der Ausdruck zur Berechnung der Eigenwerte ist einfacher als der Ausdruck für die Eigenvektoren, weshalb Park, Zhang und Denton dies als Ausgangspunkt verwendeten. Zuvor entwickelten sie eine neue Methode zur Näherungsberechnung von Eigenwerten. Darauf aufbauend stellten sie fest, dass lange Ausdrücke für Eigenvektoren aus früheren Arbeiten Kombinationen dieser Eigenwerte entsprachen. Alles in allem kann man „Neutrinoschwingungen in Materie einfach und schnell berechnen“, sagte Zhang.

In Bezug darauf, wie sie das Muster sahen, aus dem die Formel folgt, sind sich die Physiker nicht ganz sicher. Park sagt, dass sie einfach einzelne Manifestationen des Musters bemerkt und es verallgemeinert haben. Er gibt auch zu, dass er gut darin ist, Rätsel zu lösen. Er ist Mitautor einer weiteren wichtigen , 1986 entdeckten Regelmäßigkeit , die Berechnungen auf dem Gebiet der Teilchenphysik ermöglichte und Wissenschaftler bis heute zu neuen Entdeckungen inspiriert.

Und doch schockierte die Tatsache, dass das seltsame Verhalten des Neutrinos zur Entstehung neuer Ideen in Bezug auf die Matrix führen könnte, viele. "Die Leute haben lange Zeit lineare Algebra gelöst", sagte Park. "Ich warte immer noch darauf, dass mir jemand eine E-Mail sendet, in der steht: Wenn Sie sich dieses wenig bekannte Werk von Cauchy ansehen, dann finden Sie diese Formel in der Notiz im dritten Anhang."

Kleiner Unterschied

Tatsächlich war eine ähnliche Formel bereits bekannt, aber niemand bemerkte sie, weil sie maskiert war.

Im September erhielt Tao eine weitere unerwartete E-Mail, diesmal von Jiyuan Zhang, einem Doktoranden der Mathematik an der Universität von Melbourne in Australien. Zhang wies auf die Existenz einer äquivalenten Formel in einem Werk hin, das er im Mai mit seinem Kurator Peter Forester schrieb, bevor die Arbeit von Tao und drei Physikern erschien. Zhang und Forrester arbeiteten auf dem Gebiet der reinen Mathematik, der Theorie der Zufallsmatrizen. Sie wandten diese Formel an und untersuchten das Problem, das mit der Lösung von Tao und seinen Kollegen im Jahr 1999 verbunden war.

Forester erklärte uns, dass diese Formel zum ersten Mal in einer anderen Form in der Arbeit von 2001 auftauchte, die von Julia Baryshnikova verfasst wurde, einer Mathematikerin, die jetzt an der Universität von Illinois in Urbana-Champaign arbeitet und auf deren Arbeit Forester und Zhang basierten. Diese Mathematiker beschrieben die Objekte ihrer Identität jedoch nicht als Eigenvektoren, sondern als Begriffe, die zur Berechnung der Eigenwerte bestimmter kleinerer Matrizen erforderlich sind, die bei der Lösung ihres Problems auftreten.

Forester nannte die Formel in seiner Arbeit mit Zhang "identisch" mit der von Tao und den drei Physikern. Tao nannte die Formeln "fast identisch" und bezog sich auf die gleiche Weise wie die beiden Seiten der Kaninchen / Enten-Illusion. "Einige Leute suchten nach Kaninchen, andere suchten nur nach Enten", sagte er.



Denton schrieb in einer E-Mail, dass die vorher existierende Formel „unserem Ergebnis nahe ist, aber nicht perfekt“. Er fügte hinzu, dass "angesichts der Bedeutung von Eigenvektoren für viele Probleme wir immer noch der Meinung sind, dass unser Ergebnis ganz anders ist als der Rest, um es als neu zu betrachten."

Vielleicht ist es nicht so seltsam, dass in dieser Gegend in einem einzigen Sommer nach mehreren Jahrhunderten eine so plötzliche Aufregung entstehen kann. "Es gibt viele Beispiele für simultane Entdeckungen in der Mathematik", sagte Tao. - Die Ergebnisse hängen irgendwie in der Luft. Und die Leute fangen einfach an, sie an den richtigen Stellen zu suchen. “