Ich habe einmal
einen Artikel geschrieben, in dem ich ein einfaches mathematisches Modell der Entwicklung eines neuronalen Netzwerks und seiner Auswahl für die Addition von Zahlen in Zahlensystemen mit Basis 2 und goldenem Schnitt beschrieben habe. Dabei stellte sich heraus, dass der goldene Schnitt besser funktioniert. Meine erste Erfahrung erwies sich als sehr schlecht, da ich einige wichtige Nuancen nicht berücksichtigte, die damit zusammenhängen, dass der Fehler nicht für ein Neuron, sondern für ein bisschen Information berücksichtigt werden sollte. Deshalb beschloss ich, mein Experiment zu verbessern und einige weitere vorzustellen Anpassungen.
- Ich entschied mich, 100 Probenpaare von 15 (Trainingsprobe) und 1000 (Testprobe) Vektoren in Zahlensystemen mit gleichmäßig verteilten Basen von 1,2 bis 2 anstelle von zwei bisher bekannten Basen zu überprüfen.
- Ich habe auch eine lineare Regression nicht nur vom Abstand von der Basis zum Goldenen Schnitt, sondern auch von der Basis selbst, der Anzahl der Koordinaten im Vektor und dem Durchschnittswert der Koordinate im Antwortvektor, durchgeführt, um die nichtlineare Abhängigkeit des Fehlers von der Basis zu berücksichtigen.
- Ich habe auch einige Stichproben nach dem Kolmogorov-Smirnov-Kriterium (ANOVe) auf Normalität überprüft, aber diese Kriterien haben gezeigt, dass die Stichproben höchstwahrscheinlich vom Gaußschen abweichen, sodass ich mich für eine gewichtete lineare Regression anstelle der üblichen entschieden habe. Die ANOVA zeigte zwar etwas weniger F als zuvor (im Bereich von 700-800 statt 800-900), das Ergebnis blieb jedoch mehr als statistisch signifikant, was bedeutet, dass mehr Tests durchgeführt werden sollten. Bei diesen Tests habe ich ein Histogramm der Verteilungsdichte der Regressionsreste und des normalen QQ erstellt - ein Diagramm der Verteilungsfunktion dieser Reste.
Diese beiden Grafiken sind:
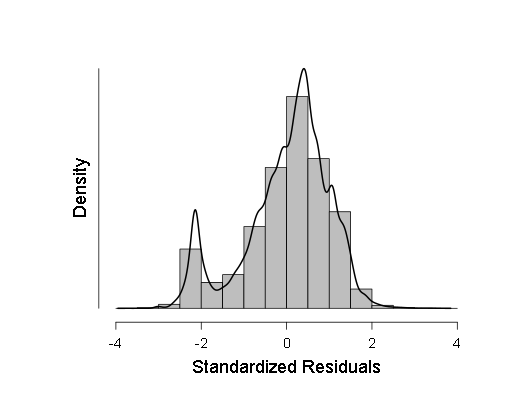
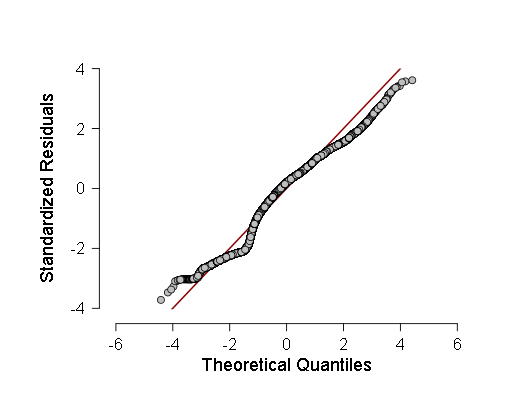
Wie zu sehen ist, ist, obwohl die Abweichung von der Normalverteilung in der Verteilung der Reste statistisch signifikant ist (und auf der linken Seite ist sogar eine kleine zweite Mode im Histogramm sichtbar), es tatsächlich sehr nahe am Gaußschen, daher ist es möglich (mit Vorsicht und größeren Konfidenzintervallen), sich auf diese lineare Regression zu verlassen .
Nun darüber, wie ich Samples zum Testen neuronaler Netze über diese generiert habe.
Hier ist der Code zum Generieren der Beispiele: Und hier ist der Header-Datei-Code: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); void calculus(double a, double x, bool *t, int n);// x a t n . void calculus(double a, double x, bool *t, int n) { int i,m,l; double b,y; b=0; m=0; l=0; b=1; int k; k=0; i=0; y=0; y=x; // t . for (i=0;i<n;i++) { (*(t+i))=false; } k=((int) (log((double)2))/(log(a)))+1;// , . while ((l<=k-1)&&(m<nk-1)) // x a ( ), { m=0; if (y>1) { b=1; l=0; while ((b*a<y)&&(l<=k-1)) { b=b*a; l++; } if (b<y) { y=yb; (*(t+kl))=true; } } else { b=1; m=0; while ((b>y)&&(m<nk-1)) { b=b/a; m++; } if ((b<y)||(m<nk-1)) { y=yb; (*(t+k+m))=true; } } } return; }
Ich habe auch beschlossen, den vollständigen Code des neuronalen Netzes zu posten: Lassen Sie uns als Nächstes darüber sprechen, wie ich eine gewichtete lineare Regression durchgeführt habe. Dazu habe ich einfach die Standardabweichungen der Ergebnisse des neuronalen Netzes berechnet und die Einheit in diese unterteilt.
Hier ist der Quellcode des Programms, mit dem ich das gemacht habe: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void) { int i; FILE *input,*output; while (fopen("input.txt","r")==NULL) i=0; input = fopen("input.txt","r");// . double mu,sigma,*x; mu=0; sigma=0; while (malloc(1000*sizeof(double))==NULL) i=0; x = (double *) malloc(sizeof(double)*1000); fscanf(input,"%lf",&mu); mu=0; for (i=0;i<1000;i++) { fscanf(input,"%lf",x+i); } for (i=0;i<1000;i++) { mu = mu+(*(x+i)); } mu = mu/1000; while (fopen("WLS.txt","w") == NULL) i=0; output = fopen("WLS.txt","w"); for (i=0;i<1000;i++) { sigma = sigma + (mu - (*(x+i)))*(mu - (*(x+i))); } sigma = sigma/1000; sigma = sqrt(sigma); sigma = 1/sigma; fprintf(output,"%10.9lf\n",sigma); fclose(input); fclose(output); free(x); return 0; };
Als nächstes fügte ich die resultierenden Gewichte der Tabelle hinzu, in der ich alle als Ergebnis des Programms erhaltenen Daten sowie die Werte der Variablen zur Berechnung der Regression reduzierte und sie dann in JASP berechnete. Hier sind die Ergebnisse:
Ergebnisse
Lineare Regression
Als nächstes habe ich ein Histogramm der Verteilungsdichte standardisierter Regressionsreste:

Sowie das normale Quantil-Quantil-Diagramm standardisierter Regressionsreste:

Dann habe ich die Durchschnittswerte der Regressionskoeffizienten, die in ihrem Verlauf erhalten wurden, auf die Variablen angewendet und meine statistische Analyse durchgeführt, um das wahrscheinlichste Minimum der Fehlerfunktion aus der Basis des Zahlensystems (wie sehr es mit diesen Variablen zusammenhängt) unter Verwendung von Fermats Lemma, Bayes-Theorem und Lagrange-Theorem zu finden wie folgt:
Tatsache ist, dass die Verteilung der Basen des Zahlensystems in der Stichprobe offensichtlich gleichmäßig war. Wenn also eine bestimmte Basis im Intervall (1,2; 2) das Minimum des mittleren quadratischen Fehlers ist, wird sie nach Fermats Lemma eine Nullableitung haben, dann die Wahrscheinlichkeitsdichte der Werte Die Funktion ist unendlich.
Nun zu meiner Anwendung des Bayes-Theorems. Ich habe die Konfidenzintervalle der Beta-Verteilung berechnet (dies ist die Wahrscheinlichkeitsverteilung von "Erfolg" im Experiment unter der Bedingung von n "Erfolgen" und m "Fehlern" mit Wahrscheinlichkeitsdichte
) die Werte der Verteilungsfunktion (dies ist die Wahrscheinlichkeit, dass die Zufallsvariable nicht größer als das Argument ist) der berechneten Fehler, basierend auf der Tatsache, dass wenn die Zufallsvariable nicht größer als das Argument ist, es "Erfolg" ist und wenn es mehr ist, dann "Misserfolg". Dann wenden wir unter Verwendung des Bayes'schen Theorems die Beta-Verteilung der Verteilungsfunktion der berechneten Fehler an und berechnen die Konfidenzintervalle [Verteilungsfunktion] von 99% für jeden berechneten Fehler.
Wir kommen zum Satz von Lagrange. Das Lagrange-Theorem besagt, dass, wenn die Funktion f (x) im Intervall [a; b] kontinuierlich differenzierbar ist, mindestens an einem Punkt dieses Intervalls eine Ableitung gleich ist
. Wie wende ich diesen Satz an: Tatsache ist, dass die Wahrscheinlichkeitsdichte eine Ableitung der Verteilungsfunktion ist, also nehme ich den Maximalwert unter denjenigen, die es genau in einigen Intervallen vom minimalen Fehler bis zu den verbleibenden Fehlern dauert. Dann berechne ich die Konfidenzintervalle solcher Werte in 98% (unter Verwendung der Bonferroni-Korrektur) unter Verwendung der folgenden Formel:
Dabei ist F1 das linke Ende des Konfidenzintervalls für die Verteilungsfunktion und F2 das rechte, x_i, x_1 sind die berechneten Fehler als Argument für die Verteilungsfunktion. Als nächstes sucht das Programm nach einem Intervall mit dem größten linken Ende und dem größten rechten Ende (so dass der Wert im Intervall maximal ist) und sucht dann nach dem Maximum und Minimum in den Basen, die den berechneten Fehlern in diesem Intervall entsprechen. Dieses Maximum und Minimum sind die Argumente der Fehlerfunktion von unten, zwischen denen das Minimum der Funktion selbst mit einer Wahrscheinlichkeit von 98% liegt.
Hier ist der Code des Programms, mit dem ich diese statistische Analyse mit Erläuterungen durchgeführt habe: Und hier ist der Header-Datei-Code: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); double Bayesian(int n, int m, double x);// - n "" m "", " " " " , : double Bayesian(int n, int m, double x) { double c; c=(double) 1; int i; i=0; for (i=1;i<=m;i++) { c = c*((double) (n+i)/i); } for (i=0;i<n;i++) { c = c*x; } for (i=0;i<m;i++) { c = c*(1-x); } c=(double) c*(n+m+1); return c; } double Bayesian_int(int n, int m, double x);// - ( ): double Bayesian_int(int n, int m, double x) { double c; int i; c=(double) 0; i=0; for (i=0;i<=m;i++) { c = c+Bayesian(n+i+1,mi,x); } c = (double) c/(n+m+2); return c; } // : void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu); void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu) { double y,y1,y2; y=(double) n/(n+m); int i; for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.5)/Bayesian(n,m,y); } mu = y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.995)/Bayesian(n,m,y); } x2=y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.005)/Bayesian(n,m,y); } x1=y; }
Hier ist das Ergebnis der Arbeit dieses Programms, als ich ihr die Grundlagen des Zahlensystems und die Ergebnisse der Regression gab:
x (- [1.501815; 1.663988] y (- [0.815782; 0.816937]
("(-" ist in diesem Fall nur eine Notation des Zeichens "Gehört" zur Mengenlehre, und eckige Klammern geben das Intervall an.)
So hat sich für mich herausgestellt, dass die beste Basis des Zahlensystems hinsichtlich der geringsten Fehleranzahl bei der Informationsübertragung im Bereich von 1,501815 bis 1,663988 liegt, das heißt, der goldene Schnitt fällt vollständig hinein. Richtig, ich habe bei der Berechnung des Minimums eine und bei der Berechnung der Informationsmenge in verschiedenen Zahlensystemen eine weitere Annahme getroffen: Erstens habe ich angenommen, dass die Fehlerfunktion von der Basis kontinuierlich differenzierbar ist, und zweitens, dass die Wahrscheinlichkeit, dass die gleichmäßig verteilte Zahl von 1 ist, 2 bis 2 haben die Nummer eins in einer bestimmten Ziffer, sie ist nach einer Nachkommastelle ungefähr gleich.
Wenn ich etwas völlig falsch oder einfach falsch gemacht habe, bin ich offen für Kritik und Vorschläge. Ich hoffe dieser Versuch war erfolgreicher.
UPD Ich habe den Artikel zweimal bearbeitet, um einige Stellen im „rein wissenschaftlichen“ Teil zu verdeutlichen, und auch den Code formatiert.
UPD2. Nach Rücksprache mit einer Person, die mit Bioinformatik vertraut ist (Absolvent des Postgraduiertenstudiums an der FBB MSU am IPPI RAS), wurde beschlossen, das Wort „Gehirn“ durch „neuronales Netzwerk“ zu ersetzen, da sie sich stark unterscheiden.