Vielleicht ist es schwierig, die geodätischen Kuppeln als ungewöhnlich oder neu zu bezeichnen. In diesem Artikel werde ich ein wenig über diese Entwürfe im Allgemeinen und über ihre Struktur sprechen und als Beispiel zeigen, wie ich etwas zu diesem Thema betrachtet habe. Der Code wird auch sein.
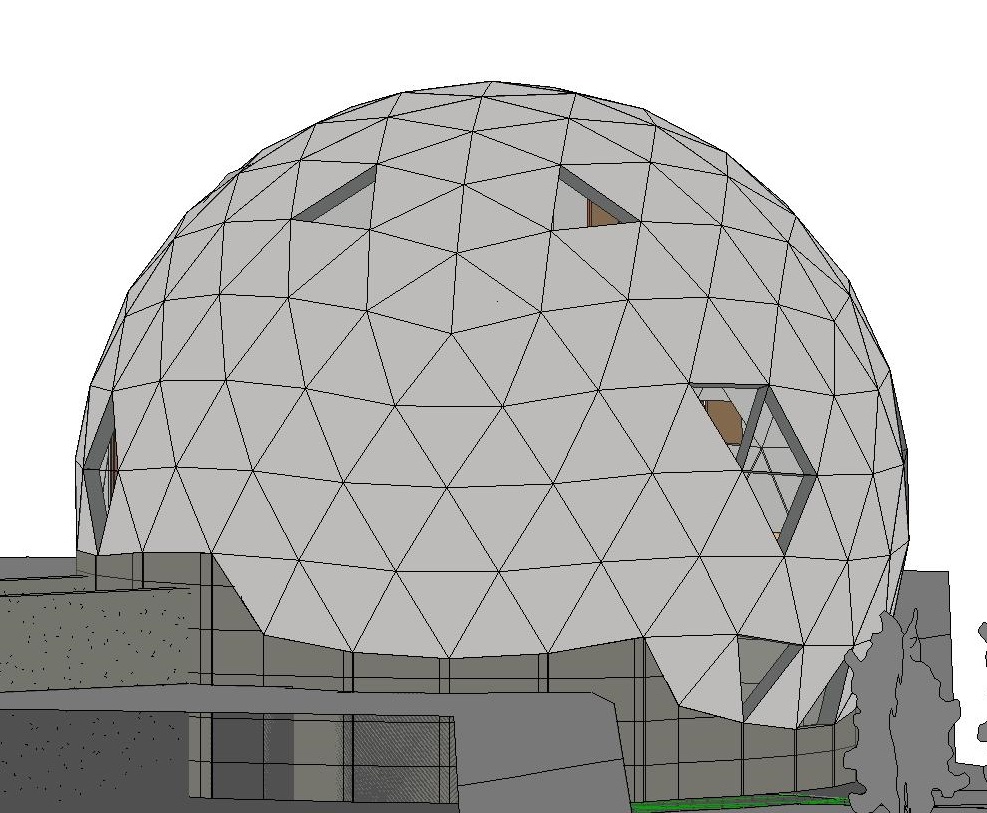
Ich werde Wikipedia nicht zitieren. Warum habe ich die Kuppel als mein Zuhause gewählt?
- Bei gleichem Volumen ist die Oberfläche der Kugel kleiner als bei jeder anderen Form. Dies wirkt sich sowohl auf den Materialverbrauch als auch auf den Energieverbrauch während des Betriebs positiv aus.
- Mir gefällt, wie die Kugel aussieht.
- Dies ist in gewisser Hinsicht ein interessantes Ingenieurprojekt, sogar eine Herausforderung. Es ist schwierig, schwierig und macht deshalb Spaß!
Wie sind diese geodätischen Bereiche im Allgemeinen angeordnet? Auf den ersten Blick scheint dies eine Art Verwebung von Kanten zu sein, und es ist schwierig, das System zu erfassen. Wir werden versuchen, das herauszufinden.
Die Basis solcher Strukturen ist das Ikosaeder oder Oktaeder. In der Regel ein reguläres Polyeder.
In meinem Fall war es genau das Ikosaeder und wird häufiger verwendet. Als nächstes nehmen wir eine Fläche und ersetzen sie durch mehrere Dreiecke, deren Eckpunkte auf einer Kugel liegen, deren Zentrum mit dem Zentrum des Ikosaeders zusammenfällt. Das hört sich nicht gut an. Lassen Sie uns abschweifen.
Es gibt einen wunderbaren Rechner
www.acidome.ru , mit dem Sie den Vermesser in Echtzeit drehen können. Nehmen Sie Ikosaeder als Basis, setzen Sie die Frequenz auf 1, Teil der Kugel 1/1.

Dies ist unser Hauptikosaeder. Frequenz ist, wie viele Teile wir jede Kante des Ikosaeders brechen werden. Wir setzen 3.4, 5 und nichts wird klar. Wechseln Sie in den Dachmodus und suchen Sie nach Fünfecken. An den Stellen, an denen wir die Spitze des Ikosaeders haben, wird es ein Fünfeck geben. Zwischen den drei Fünfecken befindet sich das Gesicht des Ikosaeders.

Wenn Sie sich die Geodäsie genau ansehen und wissen, wonach Sie suchen müssen (normalerweise ein Fünfeck), wird die Regelmäßigkeit der Struktur sichtbar. Auf der Biosphäre in Montreal können Sie mit der gebotenen Sorgfalt Pentagone finden und die Häufigkeit berechnen. Unsere Frequenz ist gleich der Anzahl der Kanten zwischen zwei Fünfecken.
Die „großen“ Dreiecke selbst, mit Eckpunkten auf den Spitzen des Ikosaeders, haben ebenfalls eine Struktur. Auf Acidome-Dächern ist dies farblich sichtbar. Dreiecke sind symmetrisch zur Mitte des „großen“ Dreiecks angeordnet. Die Anzahl ihrer Typen ist geringer als die Gesamtzahl der Dreiecke. Bei einer Häufigkeit von 5 eindeutigen Dreiecken 9.

Beim Entwerfen eines Hauses stand ich vor der Aufgabe, in Dynamo eine Kugel zu bauen. Mit diesem Tool können Sie Autodesk Revit das Arbeiten mit komplexen Formularen beibringen. Eine solche visuelle Programmierumgebung.
Beim Googeln habe ich sogar eine Skizze gefunden, die in Dynamo eine geodätische Kugel erzeugt hat. Er baute die Kugel, aber nicht diese.
Hier ist das Ding. Wenn wir eine Kante des Ikosaeders nehmen und in kleine Dreiecke teilen, kann dies auf verschiedene Arten geschehen. In acidome ist dafür der Schalter „Splitting Method“ zuständig.
Die gefundene Skizze baute die Kugel mit der Gleichakkordmethode. Was bedeutet das? Wir nehmen ein großes Dreieck des Ikosaeders, teilen jede seiner Kanten in die Anzahl der benötigten Teile auf, verbinden die Punkte an den Kanten miteinander und erhalten ein flaches Dreiecksgitter. Dann projizieren wir dieses Gitter auf die Kugel. Alles wäre in Ordnung, aber diese Dreiecke selbst haben eine ganz andere Größe. Vor allem zentral. Es ist verständlich, dass der Mittelpunkt des „großen“ Dreiecks maximal von der Kugel entfernt ist. Dies ist schlecht, da es in diesem Fall schwieriger ist, den Materialverbrauch zu optimieren. Es wird mehr Abfall geben.
Eine andere Methode zum Teilen (mit gleichen Bögen) setzt voraus, dass wir auf dem „großen“ Dreieck des Bogens aufbauen und diese bereits in gleiche Teile teilen. Der Ansatz ist anders, eine einfache Projektion geht nicht.
Die Skizze passte nicht. Ich habe versucht, das Problem zu beheben, und am Ende musste ich mit meinem Kopf in dieses Geschäft eintauchen.
Wie sich herausstellte, hat Dynamo neben der visuellen Umgebung auch Python eingebaut. Ich bin dieser Sprache noch nicht begegnet, aber wo ist unsere Sprache nicht verschwunden? Am Ende ist es nur ein Werkzeug.
Dann wird es Teile des Codes geben, bitte beachten Sie, dass dies meine Hallo-Welt in Python ist und das Ziel nicht darin bestand, die effektivste und effizienteste Lösung zu erstellen, sondern die richtige Sphäre.
Die Methode der gleichen Bögen.
Wir nehmen eine der Seiten des Ikosaeders und bilden Bögen aus den Ecken dieses Dreiecks.
for k, edge in enumerate(curves):

Dann teilen wir die Bögen in gleiche Teile und verbinden die Punkte auf den Bögen mit neuen Bögen. Alle Bögen haben ein Zentrum - das Zentrum der Kugel. Punkte sind nicht alle mit allen verbunden, sondern gleichnamig. Auf dem Bild sieht es einfacher aus als im Code.
for edge_index, point_list in enumerate(points): edge_arcs = [] for point_index, point in enumerate(point_list): next_edge_index = edge_index + 1 if len(points) == next_edge_index: next_edge_index = 0 end_point_index = n - point_index - 2 arc = Arc.ByCenterPointStartPointEndPoint(center_point, points[next_edge_index][end_point_index], point) if arc.SweepAngle > 90: arc = Arc.ByCenterPointStartPointEndPoint(center_point, point, points[next_edge_index][end_point_index]) arc_points_count = n - point_index - 1; pp = Arc.PointsAtEqualSegmentLength(arc, arc_points_count) for po in pp: on_arc_points.append(po) edge_arcs.append(arc) edges_arcs.append(edge_arcs)

Ups, und die Bögen kreuzen sich nicht! Das nicht allzu fließende Googeln brachte mich zu einem Buch, das meine Vermutungen bestätigte, dass es notwendig ist, das Zentrum eines Dreiecks, das durch die Überschneidung von Bögen gebildet wird, als oberste Kante der Geodäsie zu verwenden. Ich habe auch die Acidomquellen geraucht, kann mich aber nicht erinnern, ob ich dort eine Bestätigung gefunden habe. Ich erinnere mich, dass es interessant war.
Die Zentren müssen irgendwie gefunden werden. Dies ist das Zentrum des Dreiecks und es ist nicht schwierig, aber es war notwendig zu verstehen, wo sich diese Dreiecke auf dem Haufen von Punkten befinden. Es schien mir die einfachste Möglichkeit zu sein, die Punkte, die am nächsten beieinander liegen, miteinander zu verbinden.
for point in on_arc_points: distance = []

Nun müssen wir die Punkte, die in verschiedenen Stadien gesammelt wurden, miteinander verbinden. Dies sind die Eckpunkte der Ränder der geodätischen Kugel. Auf dem Bild sind diese Punkte deutlich sichtbar, aber wenn sie sich im Array befinden, ist alles komplizierter. Es gab mehrere Optionen, aber da die Aufgabe darin bestand, mit geringstem Aufwand ein funktionierendes Skript zu erstellen, ergab sich Folgendes:
Das Segment ist fertig. Es gibt wahrscheinlich einen richtigen Weg, um dieses Problem zu lösen, aber ich habe meinen eigenen gepflastert.

Dann entfaltet sich das Segment, es wird mehrmals kopiert und es wird eine vollständige Kugel erhalten. Hier ist eine der Wendungen:
v = Vector.ByTwoPoints(sphere_center, curves[0].StartPoint) for face_triangle in face_triangles: geodesic_sphere.append(Geometry.Rotate(face_triangle, sphere_center, v, 72))
Das Skript ist hässlich geworden, ich habe es ein paar Mal kopiert, weil beim Exportieren nach Revit Probleme aufgetreten sind. Dachte, es gab Probleme mit der Konstruktion. Infolgedessen forderte der Inder den Ukrainer auf dem Dynamo-Forum auf und alles war erfolgreich!
Jetzt können Sie eine Kugel mit jeder Frequenz und jedem Durchmesser bauen. Ein Vergleich der Größen mit den Acidom-Ergebnissen zeigte, dass alles mit hoher Genauigkeit konvergiert. Wiederholbarkeit ist gut.

Ich habe auch begonnen, Größen zu optimieren, um die Ernte zu minimieren. Da alle Größen in meinen Händen waren, war es nicht so schwierig. Infolgedessen ergab sich ein Radius der Kugel von 5,65 Metern bei einer Frequenz von 5. Mit diesen Abmessungen kann ich Materialien mit einer Breite von 125 cm sehr effektiv verwenden. Solche Breiten sind OSB-Platten, Bleche, Isolierungen und Trockenbau. Bei guter Optimierung ist die Anzahl der Ausschnitte minimal. Die besten Ergebnisse erzielen Sie, wenn Sie die Layouts der Dreiecke auf dem Material berechnen. Dies habe ich jedoch nicht getan.
Weiterhin war es einfacher, da Revit eine komplexe Form aß und es ermöglichte, mit ungefähr dem gleichen Erfolg wie mit Quadrat-Parallel zu arbeiten.
Natürlich haben die Schwierigkeiten nicht aufgehört, aber das ist eine ganz andere Geschichte.