n-Queens Completion Problem - linearer Lösungsalgorithmus

Ericgrig

Vorwort

Ich möchte das Vorwort mit Dankesworten an zwei wundervolle Programmierer aus Odessa beginnen: Andrei Kiper (Lohica) und Timur Giorgadze (Luxoft), um meine Ergebnisse in der Anfangsphase der Studie unabhängig zu verifizieren.

1. Der Artikel "Linearer Algorithmus zur Lösung des n-Queens-Abschlussproblems" wurde zu Beginn des ersten Tages des Jahres 2020 in (arXiv.org) veröffentlicht. Ursprünglich war der Artikel in russischer Sprache verfasst, daher wird hier die grundlegende Präsentation vorgestellt und dort die Übersetzung.
2. Diese Aufgabe und einige andere der vielen NP-Komplettsätze (die Aufgabe, Boolesche Formeln (3-SAT) zu erfüllen, die Aufgabe, die maximale Clique oder eine Clique einer bestimmten Größe zu finden ...) zu unterschiedlichen Zeiten waren in meinem Interesse. Ich suchte nach einer algorithmischen Lösung, die auf verschiedenen Computerexperimenten basierte, aber es gab keinen konkreten Erfolg. Es war wie ein Mensch, der zu lernen versuchte, wie man an einem Arm auf der horizontalen Stange fit wird. Es gibt kein Ergebnis, aber jedes Mal gibt es die Hoffnung, dass alles bald klappt. Das letzte Mal, als ich mich entschied, länger bei der n-Queens-Abschlussaufgabe zu bleiben (als eines der Familienmitglieder) und zu versuchen, etwas zu tun. Es ist angebracht, sich an den wunderbaren Odessa-Witz zu erinnern: "In einem überfüllten Bus, der abends auf einer holprigen Straße in die Vororte zurückkehrt, ist eine Frauenstimme zu hören - Mann, wenn Sie mich völlig überfallen haben, dann tun Sie wenigstens etwas."
3. Das Studium dauerte lange genug - fast eineinhalb Jahre. Dies liegt zum einen daran, dass andere Aufgaben im Forschungsprozess berücksichtigt wurden, zum anderen gab es auf dem Weg schwierige Fragen, ohne die wir nicht weiterkommen könnten. Ich werde einige von ihnen auflisten:
   
   
   • Es gibt n Zeilen in der Entscheidungsmatrix. In welcher Reihenfolge sollte der Zeilenindex ausgewählt werden, wenn die Anzahl der Möglichkeiten für eine solche Auswahl n beträgt!
   • Wenn eine Reihe erstellt wird, sollte die verbleibende freie Position in dieser Reihe ausgewählt werden, da die Anzahl der Möglichkeiten für eine solche Auswahl so groß ist, dass sie als „enger Verwandter“ der Unendlichkeit angesehen werden kann (z. B. die Anzahl der Möglichkeiten, eine freie Position in allen Reihen für ein Schachbrett der Größe 100 auszuwählen x 100 ist ungefähr 10 ¹²⁴ )
   • Zusammen bilden diese beiden Indikatoren einen Zustandsraum (einen Auswahlraum). Es sieht so aus, als gäbe es riesige Möglichkeiten, Sie können wählen, was Sie wollen. Hinter jeder spezifischen Auswahl bei jedem Schritt steht jedoch ein anderes Problem - die Einschränkung der Auswahl in allen nachfolgenden Schritten. Darüber hinaus ist dies in den letzten Phasen der Problemlösung besonders heikel. Wir können sagen, dass die Entscheidungsmatrix "rachsüchtig" ist. Alle „unbewussten Fehler“, die Sie bei der Auswahl in den vorherigen Phasen gemacht haben, werden „akkumuliert“. Am Ende der Entscheidung zeigt sich dies in der Tatsache, dass in den Zeilen, in denen Sie die Königin platzieren sollten, keine leeren Positionen mehr vorhanden sind und der Suchzweig zum Stillstand kommt . Hier, wie bei Zhvanetsky: "Ein falscher Zug, und Sie sind schwanger."
   • Wenn der Zweig der Suche nach einer Lösung zum Stillstand kommt, haben wir die Möglichkeit, zu einigen der vorherigen Positionen zurückzukehren (Back Tracking), so dass wir von dieser Position aus wieder mit der Bildung des Zweigs der Suche nach einer Lösung beginnen. Dies ist eine natürliche „Eigenschaft“ nicht deterministischer Probleme. Die Frage ist, welche der vorherigen Ebenen zurückgegeben werden sollen. Dies ist das gleiche offene Problem wie die Frage der Auswahl des Zeilenindex oder der Auswahl einer freien Position in dieser Zeile.
   • Schließlich sollte ein Problem in Bezug auf die Geschwindigkeit des Algorithmus festgestellt werden. Es wäre traurig, wenn es kein Ziel gäbe, schnell laufende Algorithmen zu entwickeln. Bei der Modellierung war es nicht möglich, einen Algorithmus zu entwickeln, der in allen Bereichen der Problemlösung schnell und effizient funktioniert. Ich musste drei Algorithmen entwickeln. Sie übertragen die Ergebnisse wie ein Schlagstock aufeinander. Einer von ihnen arbeitet sehr schnell, aber unhöflich, der andere - im Gegenteil, arbeitet langsam, aber effizient. Jeder von ihnen arbeitet in der „Zone ihrer Verantwortung“.
4. Der Zweck der Studie bestand zunächst nur darin, zumindest eine Lösung zu finden. Ich musste viel herausfinden, bevor die erste Lösung entwickelt wurde. Es dauerte mehr als vier Monate. Es war möglich dort anzuhalten, das Ziel wurde erreicht - na ja, okay. Es schien mir jedoch, dass nicht alle Möglichkeiten einer algorithmischen Lösung dieses Problems ausgeschöpft waren. Natürlich bestand der Wunsch, den entwickelten Algorithmus so zu verbessern, dass die zeitliche Komplexität des Algorithmus linear-O (n) war. Als eine solche lineare Lösung gefunden wurde, gab es "einen weiteren Wunsch" - die Anzahl der Fälle zu reduzieren, in denen das Back Tracking (BT) -Verfahren bei der Bildung des Lösungssuchzweigs verwendet wurde. Es war ein "unverschämter" Wunsch, die Aufgabe von nicht deterministisch auf bedingt determiniert (so weit wie möglich) zu übertragen. Es hat lange gedauert, aber das Ziel wurde beispielsweise im Bereich der Schachbrettgrößenwerte n = (320, ..., 22500) erreicht, die Anzahl der Fälle, in denen das BT-Verfahren nie angewendet wird, beträgt mehr als 50%. Es stellt sich heraus, dass in 50% der Fälle, in denen das Programm gestartet wird, der Algorithmus „absichtlich“ eine Lösung bildet und niemals „stolpert“. (Ich erinnere mich an das Märchen über den Goldfisch und dachte über diese beiden Wünsche nach ...)
5. Beim Vergleich der Veröffentlichungen, die ich während der Recherche kennenlernen durfte, kam ich zu dem Ergebnis, dass dieses Problem und andere Probleme dieser Art nicht auf der Grundlage eines rigorosen mathematischen Ansatzes gelöst werden können, d. H. Nur auf der Grundlage von Definitionen, Lemmasätzen und Theoremsätzen. In dem Artikel gibt es eine "philosophische Bemerkung" dazu. Ich bin mir sicher, dass viele Probleme aus den vielen NP-Complete nur auf der Basis algorithmischer Mathematik mit Hilfe von Computersimulationen gelöst werden können. Eine solche Schlussfolgerung bedeutet nicht, die Mathematik einzuschränken, sondern vielmehr, die Fähigkeiten der Mathematik durch die Entwicklung algorithmischer mathematischer Methoden zu erweitern. Für jede Familie von Problemen müssen Sie Ihren eigenen angemessenen mathematischen Ansatz verwenden. (Warum sollte man einen Doktoranden beauftragen, ein Problem aus der NP-Complete-Familie zu lösen, ohne algorithmische Mathematik und Computermodellierungsmethoden anzuwenden, wenn bekannt ist, dass aus einem solchen Unterfangen eigentlich nichts wird?)
6. Jeder Algorithmus (Programm) hat eine einfache Eigenschaft - entweder funktioniert er oder nicht! Ich möchte die Mitglieder unserer Habro-Community ansprechen, die einen Computer mit Matlab in der Barrierefreiheit installiert haben. Ich möchte Sie bitten, die Funktionsweise des in Betracht gezogenen Algorithmus zur Lösung des n-Queens-Abschlussproblems zu testen. Dies dauert nur 5-10 Minuten. Um den Algorithmus zu testen, müssen Sie einige einfache Schritte ausführen:
   
   
   • Generiere eine zufällige Komposition aus k Königinnen und überprüfe die Korrektheit dieser Komposition.
   • Vervollständigen Sie diese Zusammensetzung auf der Grundlage des vorgeschlagenen Entscheidungsalgorithmus zu einer vollständigen Lösung. Oder das Programm muss entscheiden, dass diese Zusammensetzung keine Lösung hat.
   • Überprüfen Sie die Richtigkeit der durch die Konfiguration erhaltenen Lösung.
   
   
   Sie müssen für solche Tests keinen Code schreiben. Zusätzlich zum Hauptprogramm habe ich zwei weitere Programme in der Matlab-Sprache vorbereitet:
   
   1. Generarion_k_Queens_Composition - Erzeugung einer zufälligen Komposition der Größe k für ein beliebiges Schachbrett der Größe nxn
   
   2. Completion_k_Queens_Composition.m - Vervollständigen einer beliebigen Komposition bis zu einer vollständigen Entscheidung oder Entscheiden, dass diese Komposition keine Lösung hat ( Hauptprogramm ).
   
   3. Validation_n_Queens_Solution.m - Überprüfung der Richtigkeit der Lösung des n-Queens-Problems oder der Richtigkeit der Zusammensetzung von k Königinnen.
   
   Sie arbeiten sehr schnell. Zum Beispiel für ein Schachbrett mit einer Größe von 1000 x 1000 Zellen, die Gesamtzeit, die durchschnittlich benötigt wird, um eine beliebige Zusammensetzung zu erzeugen (0,0015 s), diese Zusammensetzung zu vervollständigen (0,0622 s) und die Richtigkeit der erhaltenen Lösung zu überprüfen (0,0003 s). 0,1 Sekunden nicht überschreitet. (Ausgenommen die Zeit, die zum Herunterladen der Daten oder Speichern der Ergebnisse benötigt wird.)
   
   Schicken Sie mir eine E-Mail (ericgrig@gmail.com), wenn Sie die Möglichkeit haben, einem Freund zu helfen, sende ich Ihnen diese drei Programme umgehend zu. Ich bin allen Kollegen dankbar, die den Algorithmus objektiv testen und ihre Meinung in der Diskussion äußern können.
7. Ich habe den Quellcode des Programms mit detaillierten Kommentaren erstellt, die hoffentlich bald auf Habré veröffentlicht werden. Ich denke, dass diejenigen, die an der Lösung komplexer Probleme aus der NP-Complete- Familie interessiert sind, etwas Interessantes für sich finden.
8. Ich möchte noch einmal an die Mitglieder der Habr-Gemeinschaft appellieren, aber aus einem anderen Grund. Hier in Marseille (Frankreich) wird das Team der France Fold Group gebildet , mit dem Algorithmen zur Vorhersage der physikochemischen Eigenschaften von Verbindungen mit hohem Molekulargewicht erforscht und entwickelt werden sollen. Ich denke, es ist nicht wert zu sagen, dass dies eine ziemlich schwierige Aufgabe mit einer langen Geschichte ist und dass ernsthafte Teams in verschiedenen Ländern an diesem Problem arbeiten, einschließlich des Khasabis- Teams von Deep Mind (Sie können den Artikel auf Habré (habr.com_Folding) sehen) . Ziel ist es, ein starkes Team zu bilden, das keine Angst vor der Lösung komplexer Probleme hat. Die Form der Organisation der gemeinsamen Arbeit ist verteilt. Jedes Teammitglied lebt in seiner Stadt und arbeitet in seiner Freizeit an dem Projekt. Wir brauchen Programmierer und Forscher (Physiker, Chemiker, Mathematiker, Biologen). ) usw. osto "rücksichtslose" Programmierer- (squared). Schreiben Sie mir, wenn Sie es interessant finden, die oben ist meine E-Mail. Ausführlicher kann ich im Antwortschreiben erzählen.

Das Vorwort zum Artikel war genauso lang wie der Artikel. Das Format der Familienpräsentation auf Habré ermöglicht es mir, meine Gedanken freier auszudrücken, aber gemessen an der Größe habe ich es ziemlich frei ausgenutzt. Ich wollte kurz schreiben, aber "es stellte sich heraus wie immer."

PS Ich dachte, dass die Mitglieder der Habr-Community interessiert wären, auf welche Schwierigkeiten ich stieß, wenn ich die Ergebnisse der Studie veröffentlichen wollte. Als der Artikel erstellt wurde, habe ich ihn gemäß den Anforderungen des Journal of Artificial Intelligence Research (JAIR) in das .tex-Format umformatiert und dorthin gesendet. Früher gab es Veröffentlichungen zu einem ähnlichen Thema. Besonders hervorzuheben ist der Artikel C. Gent, I.-P. Jefferson und P. Nightingale (2017) (Komplexität der Fertigstellung von n-Königinnen) , in denen die Autoren bewiesen haben, dass das betreffende Problem zum NP-Complete-Set gehört, und über die Schwierigkeiten bei der Lösung dieses Problems sprachen. In den Schlussfolgerungen schreiben die Autoren: „Für jeden, der die Regeln des Schachs versteht, kann die n-Queens-Vervollständigung eines der natürlichsten NP-Complete-Probleme von allen sein.“ ( Für jeden, der die Regeln des Schachs versteht, kann die n-Queens-Vervollständigungsaufgabe eine von ihnen werden die natürlichsten NP-Complete Aufgaben ).

Nach 10 Tagen erhielt ich eine Absage von JAIR mit dem Wortlaut: "Der Artikel entspricht nicht dem Format der Zeitschrift." Ich habe den Artikel nicht einmal in Betracht gezogen. Mit einer solchen Antwort habe ich nicht gerechnet. Ich dachte, wenn eine Zeitschrift Artikel veröffentlicht, in denen die Autoren zu dem Schluss kommen, dass es sehr schwierig ist, ein bestimmtes Problem zu lösen, und keine konkrete Lösung liefert, wird der Artikel, der einen effektiven Lösungsalgorithmus liefert, mit Sicherheit zur Prüfung angenommen. Die Redaktion hatte jedoch eine eigene Meinung zu diesem Thema. (Ich glaube, dass dort kompetente Spezialisten arbeiten, und höchstwahrscheinlich wurden sie durch den „unverschämten“ Titel des Artikels und alles, was dort steht, in Frage gestellt. Wir dachten, „es liegt höchstwahrscheinlich ein Fehler vor und schickten mich vorsichtig weg, bezogen auf das Format ").

Ich musste mich für eine andere von Experten begutachtete periodische wissenschaftliche Veröffentlichung zu relevanten Themen entscheiden. Hier bin ich mit der harten Realität konfrontiert. Fakt ist, dass ungefähr 80% aller Zeitschriften bezahlt werden: Entweder muss ich einen anständigen Betrag an die Zeitschrift zahlen, damit der Artikel für alle Leser frei verfügbar ist, oder sie müssen den Artikel als Geschenk "in the bow" geben und sie werden jeden in Rechnung stellen, der möchte diese Studie kennenlernen. Und die erste und die zweite Option sind für mich grundsätzlich inakzeptabel. Ich fühlte mich gut mit dieser Art des Verlagsschlägers, als ich versuchte, mich mit einigen Veröffentlichungen vertraut zu machen.

Die nächste Zeitschrift, die sich zum Prinzip des freien Zugangs zu Informationen bekennt, war das SMAI Journal of Computational Mathematics . Sie weigerten sich auch mit dem gleichen Wortlaut, wenn auch viel schneller - in zwei Tagen.

Dann wurde eine Zeitschrift ausgewählt: Diskrete Mathematik und Theoretische Informatik . Hier sind die Anforderungen einfach: Zuerst müssen Sie den Artikel in arXiv.org veröffentlichen und erst danach müssen Sie den Artikel zur Prüfung registrieren. Okay, wir werden die Regeln befolgen - ich habe einen Artikel in arXiv.org eingereicht. Sie schrieben mir, dass sie den Artikel in 8 Stunden veröffentlichen würden. Dies geschah jedoch nicht nach 8 Stunden, nicht nach 8 Tagen. Der Artikel wurde von den Mentoren „festgehalten“ und erst nach 9 Tagen veröffentlicht. Es gab keine Beschwerden in Form und Inhalt des Artikels. Ich denke, wie im Fall von JAIR hatten Mentoren Zweifel an der Möglichkeit, "dies zu tun und darüber zu schreiben". Einige Zeit später wurde der Artikel nach Korrektur technischer Fehler aktualisiert und in seiner endgültigen Form in der Neujahrsnacht veröffentlicht.

Ich muss im Detail darauf eingehen, um zu zeigen, dass es zum Zeitpunkt der Veröffentlichung der Forschungsergebnisse Probleme geben kann, die sich nicht logisch erklären lassen.

Das Folgende ist ein Artikel, dessen Übersetzung ins Englische unter (arXiv.org) veröffentlicht wurde .

1. Einleitung

Unter den verschiedenen Möglichkeiten, das n-Queens-Problem zu formulieren, nimmt die betreffende n-Queens-Completion- Aufgabe aufgrund ihrer Komplexität eine Sonderstellung ein. In ihrer Arbeit (Gent at all (2017)) zeigte sich, dass das n-Queens Completion-Problem zur Menge NP-Complete gehört ( zeigte, dass n-Queens Completion sowohl NP-Complete als auch # P-Complete ist ). Es wird davon ausgegangen, dass die Lösung dieses Problems uns den Weg zur Lösung einiger anderer Probleme aus dem Satz von NP-Complete ebnen kann .

Das Problem wird wie folgt formuliert. Es gibt eine Komposition von k Königinnen, die gleichmäßig auf einem Schachbrett der Größe nxn verteilt sind . Es muss nachgewiesen werden, dass diese Zusammensetzung zu einer vollständigen Lösung vervollständigt werden kann, und es muss mindestens eine Lösung angegeben werden, oder es muss nachgewiesen werden, dass eine solche Lösung nicht existiert. Mit Konsistenz ist hier eine Zusammensetzung von k Königinnen gemeint, für die drei Bedingungen des Problems erfüllt sind: In jeder Reihe, jeder Spalte und auch auf der linken und rechten Diagonale, die durch die Zelle gehen, in der sich die Königin befindet, befindet sich nicht mehr als eine Königin. Das Problem in dieser Form wurde erstmals von Nauk (1850) formuliert.

1.1 Definitionen

Im Folgenden werden wir die Größe der Seite des Schachbretts mit dem Symbol n bezeichnen . Eine Lösung wird als vollständig bezeichnet, wenn alle n Königinnen konsistent auf einem Schachbrett platziert sind. Bei allen anderen Lösungen wird die Komposition aufgerufen, wenn die Anzahl k der korrekt platzierten Königinnen kleiner als n ist . Wir bezeichnen eine Zusammensetzung von k Königinnen als positiv, wenn sie vor einer vollständigen Lösung abgeschlossen werden kann. Dementsprechend wird eine Zusammensetzung, die erst mit einer vollständigen Lösung abgeschlossen werden kann, als negativ bezeichnet. Als Analogie zu einem "Schachbrett" der Größe nxn betrachten wir auch eine "Lösungsmatrix" der Größe nxn . Als Beispiel werden alle zur Lösung des Problems entwickelten Algorithmen in der Matlab-Sprache dargestellt.

Die Studie wurde auf der Basis einer Computersimulation (Computersimulation) durchgeführt. Um diese oder jene Hypothese zu testen, führten wir Rechnerexperimente in einem weiten Bereich von Werten n = (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10000, 30 000, 50 000, 80 000, 10 ⁵ , 3 · 10 ⁵ , 5 · 10 ⁵ , 10 ⁶ , 3 · 10 ⁶ , 5 · 10 ⁶ , 10 ⁷ , 3 · 10 ⁷ , 5 · 10 ⁷ , 8 * 10 ⁷ , 10 ⁸ ) und in Abhängigkeit von dem Wert von n wurden ausreichend große Proben zur Analyse erzeugt. Wir bezeichnen eine solche Liste als " Basisliste von n Werten " für die Durchführung von Computerexperimenten. Alle Berechnungen wurden auf einem normalen Computer durchgeführt. Zum Zeitpunkt der Montage (Anfang 2013) war die Konfiguration recht erfolgreich: CPU - Intel Core i7-3820, 3,60 GH, RAM-32,0 GB, GPU-NVIDIA GeForse GTX 550 Ti, Festplattengerät - ATA Intel SSD, SCSI, OS- 64-Bit-Betriebssystem Windows 7 Professional . Wir nennen dieses Kit einfach - Desktop-13 .

2. Datenaufbereitung

Der Algorithmus beginnt mit dem Lesen einer Datei, die ein eindimensionales Array von Daten zur Verteilung einer beliebigen Zusammensetzung von k Königinnen enthält. Es wird davon ausgegangen, dass die Daten auf folgende Weise aufbereitet werden. Es gebe ein Array mit Nullen Q (i) = 0, i = (1, ..., n) , wobei die Indizes der Zellen dieses Arrays den Zeilenindizes der Lösungsmatrix entsprechen. Befindet sich in einer beliebigen Zeile i der Lösungsmatrix eine Dame in Position j , so wird die Zuordnung Q (i) = j durchgeführt. Somit ist die Zusammensetzungsgröße k gleich der Anzahl von Nicht-Null-Zellen des Arrays Q. (Zum Beispiel bedeutet Q = (0, 0, 5, 0, 4, 0, 0, 3, 0, 0) , dass wir eine Zusammensetzung von k = 3 Königinnen auf der Matrix n = 10 betrachten , wobei sich die Königinnen in der 3. befinden. 5. und 8. Zeile in den Positionen: 5, 4, 3).

3. Algorithmus zur Überprüfung der Richtigkeit des n-Queens-Lösungsproblems

Für die Forschung brauchen wir einen Algorithmus, mit dem wir in kurzer Zeit die Richtigkeit der Lösung des n-Queens-Problems bestimmen können. Die Position der Königinnen in jeder Reihe und jeder Spalte ist einfach zu steuern. Die Frage betrifft diagonale Grenzen. Wir könnten einen effektiven Algorithmus für eine solche Abrechnung entwickeln, wenn wir jede Zelle der Lösungsmatrix einer bestimmten Zelle eines bestimmten Kontrollvektors zuordnen könnten, der den Einfluss diagonaler Beschränkungen auf die betreffende Zelle eindeutig charakterisieren würde. Dann kann basierend darauf, ob die Zelle des Steuervektors frei oder besetzt ist, beurteilt werden, ob die entsprechende Zelle der Entscheidungsmatrix frei oder geschlossen ist.Eine solche Idee wurde zuerst von Sosic & Gu (1990) verwendet , um die Anzahl der Konfliktsituationen zwischen verschiedenen Positionen von Königinnen zu berücksichtigen und zu akkumulieren. Wir verwenden eine ähnliche Idee in dem unten dargestellten Algorithmus, jedoch nur, um zu berücksichtigen, ob die Zelle der Lösungsmatrix frei oder belegt ist. Abbildung 1 zeigt als Beispiel ein 8 x 8- Schachbrett, über dem sich eine Folge von 24 Zellen befindet .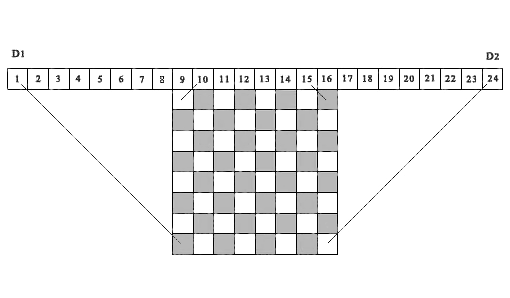


Abb.1. Ein Demo-Beispiel für die Entsprechung der diagonalen Projektionen der Matrixzellen zu den entsprechenden Zellen der Kontrollfelder D1 und D2 . ( N = 8)

Betrachten Sie die ersten 15 Zellen als Elemente des Kontrollvektors D1 . Die Projektionen aller linken Diagonalen von irgendeiner Zelle der Lösungsmatrix fallen in eine der Zellen des Kontrollvektors D1 . Tatsächlich befinden sich alle derartigen Vorsprünge innerhalb von zwei parallelen Liniensegmenten, von denen eines die Matrixzelle (8.1) mit der ersten Zelle des Vektors D1 und das zweite die Matrixzelle (1.8) mit der 15. Zelle des Steuervektors D1 verbindet. Wir geben eine ähnliche Definition für die rechten diagonalen Projektionen. Verschieben Sie dazu die Referenz von Zelle 1 nach Zelle 9 nach rechts und betrachten Sie die Folge von 16 Zellen als Elemente des Kontrollvektors D2 (in der Abbildung sind dies Zellen vom 9. bis zum 24.) Projektionen aller rechten Diagonalen von einer beliebigen Zelle der Matrix Die Lösungen fallen in eine der Zellen dieses Kontrollvektors, beginnend von der 2. bis zur 16. Zelle (in der Abbildung vom 10. bis zum 24.). Hierbei liegen alle derartigen Vorsprünge zwischen zwei parallelen Liniensegmenten - dem Segment, das die Zelle (8, 8) der Lösungsmatrix mit der Zelle 16 des Vektors D2 (Zelle 24 in der Figur) verbindet, und dem Segment, das die Zelle (1,1) der Lösungsmatrix mit der Zelle verbindet 2 Steuervektoren D2(Zelle 10 in der Figur). Die Projektionen aller Zellen der Lösungsmatrix, die auf derselben linken Diagonale liegen, fallen jeweils in dieselbe Zelle des linken Kontrollvektors D1 , die Projektionen aller Zellen der Lösungsmatrix, die auf derselben rechten Diagonale liegen, fallen in dieselbe Zelle Zelle des rechten Kontrollvektors D2 . Somit ermöglichen diese beiden Steuervektoren D1 und D2 die vollständige Kontrolle aller diagonalen Hemmungen für jede Zelle der Entscheidungsmatrix.

Es ist wichtig anzumerken, dass die Idee, diagonale Projektionen auf Zellen von Steuervektoren zu verwenden, um zu bestimmen, ob eine Zelle einer Lösungsmatrix mit Koordinaten (i, j) frei oder besetzt ist, auch später in implementiert wurdeRichards (1997) . Es bietet einen der schnellsten rekursiven Suchalgorithmen für alle Lösungen, basierend auf Operationen mit einer Bitmaske. Ein wichtiger Unterschied besteht darin, dass der angegebene Algorithmus für die sequentielle Suche aller Lösungen ab der ersten Zeile der Lösungsmatrix nach unten oder ab der letzten Zeile der Matrix nach oben ausgelegt ist. Der von uns vorgeschlagene Algorithmus basiert auf der Bedingung, dass die Wahl der Nummer jeder Zeile für den Ort der Königin willkürlich sein muss. Für den betrachteten Algorithmus ist dies von grundlegender Bedeutung. Beachten Sie, dass die obige Abbildung 1 in Analogie zu dem aufgebaut ist, was in diesem Artikel veröffentlicht wird.
Ein Programm, um zu überprüfen, ob eine gegebene Lösung des n-Queens-Problems korrekt ist oder ob eine gegebene Zusammensetzung aus k wahr istQueens ist wie folgt.

1. Um diagonale Hemmungen zu steuern, erstellen Sie zwei Arrays D1 (1: n2) und D2 (1: n2) , wobei n2 = 2 * n ist, und ein Array B (1: n) , um die Belegung der Spalten der Lösungsmatrix zu steuern. Setzen Sie diese drei Arrays außer Kraft.

2. Wir führen den Zähler der Anzahl der korrekt installierten Königinnen ein ( totPos = 0 ). Ausgehend von der ersten Zeile werden in einem Zyklus konsequent alle Positionen der Königinnen berücksichtigt. Wenn Q (i)> 0 ist , dann bilden wir basierend auf dem Index der Zeile i und dem Index der Position der Königin in dieser Zeile j = Q (i) die entsprechenden Indizes für die Steuerfelder D1 (r) und D2 (t) :
r = n + j - i
t = j + i

3. Wenn alle Bedingungen ( D1 (r) = 0, D2 (t) = 0, B (j) = 0 ) erfüllt sind , bedeutet dies, dass die Zelle ( i, j) ist frei und fällt nicht in die Projektionszone von diagonalen Beschränkungen, die von zuvor festgelegten Königinnen gebildet werden. Die Position der Königin in dieser Position ist korrekt. Wenn mindestens eine dieser Bedingungen nicht erfüllt ist, ist die Wahl einer solchen Position jeweils falsch, und die Entscheidung ist falsch.

4. Wenn die Lösung korrekt ist, erhöhen Sie den Zähler der Anzahl der korrekt installierten Königinnen ( totPos = totPos + 1 ) und schließen Sie die entsprechenden Zellen der Kontrollfelder: (D1 (r) = 1, D2 (t) = 1, B (j) = 1) . Also schließen wir alle Zellen in der Spalte(j) und die Zellen der Lösungsmatrix, die sich entlang der linken und rechten Diagonalen befinden, die sich in der Zelle (i, j) schneiden .

5. Wiederholen Sie den Überprüfungsvorgang für alle verbleibenden Positionen.
Vielleicht ist dies einer der schnellsten Algorithmen zur Bewertung der Richtigkeit der Lösung des n-Queens-Problems . Die Überprüfungszeit von einer Million Positionen für die Matrix der Lösungen 10 ⁶ x 10 ⁶ auf dem Desktop-13 beträgt 0,175 Sekunden, was ungefähr der Zeit entspricht, in der die Eingabetaste gedrückt wurde. Offensichtlich ist dieser Algorithmus in Bezug auf die Zählzeit in Bezug auf n linear .

4. Beschreibung des Algorithmus zur Lösung des Problems

Der General . Das n-Queens-Vervollständigungsproblem ist ein klassisches nicht deterministisches Problem. Die Hauptschwierigkeit seiner Lösung hängt mit dem Problem der Auswahl des Zeilenindex und des Positionsindex in dieser Zeile zusammen, wenn der Zustandsraum sehr groß ist. Bei der Suche nach allen möglichen Lösungen tritt ein solches Problem nicht auf. Wir müssen alle gültigen Suchzweige im Zustandsraum berücksichtigen, und die Reihenfolge, in der sie berücksichtigt werden, spielt keine Rolle. Wenn jedoch eine beliebige Zusammensetzung von k Königinnen bis zu einer vollständigen Lösung vervollständigt werden muss, benötigen wir in diesem Fall einen Algorithmus zum Auswählen von Zeilen- und Spaltenindizes, der die vorhandene Zusammensetzung angemessen wahrnimmt und zu einer Lösung führt, die schneller als andere ist. In diesem Projekt haben wir die Frage der Wahl auf der Grundlage der folgenden allgemeinen Position entschieden: Wenn wir keine Bedingungen formulieren können, die einer Zeile oder einer Position in dieser Zeile den Vorrang vor anderen geben, verwenden wir einen Zufallsauswahlalgorithmus auf der Grundlage von gleichmäßig verteilte Zufallszahlen . Eine ähnliche Zufallsauswahlmethode zur Lösung von Problemen, bei denen der Zustandsraum sehr groß ist, ist ganz natürlich. Eine der Ausgaben der Reihe Proceedings of a DIMACS Workshop (1999) widmete sich ganz der Verwendung der Zufallsauswahl bei der Entwicklung von Algorithmen zur Lösung komplexer Probleme. Die korrekte Implementierung des Zufallsauswahlalgorithmus kann eine ziemlich produktive Lösung sein, obwohl dies eine notwendige, aber nicht ausreichende Bedingung für die Vervollständigung der Lösung ist. Sosic und Gu (1990) verwenden als eine der ersten Studien einen Zufallsauswahlalgorithmus zur Lösung des n-Queens-Problems . Der untersuchte Algorithmus basiert auf einer relativ einfachen und prägnanten Idee. Es gebe eine Folge von Zahlen von 1 bis n , die zufällig neu angeordnet werden. Eine solche Menge von Zahlen hat eine wichtige Eigenschaft. Es besteht darin, dass unabhängig davon, wie diese Zahlen auf verschiedene Zeilen der Lösungsmatrix verteilt sind, wie die Positionen der Königin (eine Zahl pro Zeile), die ersten beiden Regeln in der Aussage des Problems immer erfüllt sind: Jede Zeile und jede Spalte haben keine mehr als eine Königin. Es wird jedoch nur ein Teil der so erhaltenen Positionen frei von diagonalen Beschränkungen sein. Der andere Teil befindet sich in einem Konflikt mit zuvor eingerichteten Königinnen. Um aus dieser Situation herauszukommen, verwendeten die Autoren die Methode, gegensätzliche Positionen zu vergleichen und auszutauschen, um eine vollständige Lösung zu erhalten. In unserem vorgeschlagenen Algorithmus sind Konfliktsituationen unmöglich, da bei jedem Schritt zur Lösung des Problems die Königin nur dann in die Zelle der betreffenden Leitung installiert wird, wenn die Zelle frei ist.

4.1 Auswählen eines Modells für die Rückverfolgung (BT)

Beim Finden einer Lösung für ein Problem kann eine Situation auftreten, in der eine sequentielle Lösungskette zu einer Sackgasse führt. Dies ist eine „genetische“ Eigenschaft nicht deterministischer Probleme. In diesem Fall müssen Sie zu einem der vorherigen Schritte zurückkehren, den Status der Aufgabe gemäß dieser Ebene wiederherstellen und die Suche nach einer Lösung von dieser Position aus erneut starten. Die Frage ist, welches der vorherigen Level zurückgegeben werden soll und wie viele solcher Level es sein sollen (mit Level meinen wir einen bestimmten Schritt bei der Lösung des Problems mit einer bestimmten Anzahl korrekt installierter Königinnen). Offensichtlich ist die Auswahl einer Lösungsebene zum Zurückgehen genauso relevant wie die Auswahl eines Zeilenindex oder eines Positionsindex in dieser Zeile. Unabhängig von der Vorgehensweise zur Lösung dieses Problems ist es daher erforderlich, zunächst die Anzahl der Grundstufen für die Rückkehr sowie den Mechanismus und die Bedingungen für die Rückkehr zu einer dieser Stufen zu bestimmen. In unserem vorgeschlagenen Algorithmus unterteilen wir die Lösungsmatrix in drei Grundebenen. Dies sind die Rückgabestellen. Wenn aufgrund der Lösung ein Deadlock auftritt, kehren wir abhängig von den Parametern der Aufgabe zu einer dieser drei grundlegenden Ebenen zurück. Die erste Basisebene ( baseLevel1 ) entspricht dem Zustand, in dem die Datenüberprüfung der betreffenden Zusammensetzung abgeschlossen ist. Dies ist der Beginn des Programms. Die Werte der folgenden zwei Basisebenen ( baseLevel2 und baseLevel3 ) hängen von der Größe der Matrix n ab . Die empirische Abhängigkeit dieser Grundwerte von der Größe der Lösungsmatrix wurde anhand einer Vielzahl von Rechnerexperimenten ermittelt. Zur genaueren Darstellung dieser Abhängigkeit haben wir das gesamte betrachtete Intervall von 7 bis 10 ⁸ in zwei Teile geteilt. Sei u = log (n) , dann wenn n <30 000 , dann

baseLevel2 = n - rund (12.749568 * u3 - 46.535838 * u2 + 120.011829 * u - 89.600272)
baseLevel3 = n - rund (9.717958 * u3 - 46.144187 * u2 + 101.296409 * u - 50.669273)

ansonsten

baseLevel2 = n - rund (-0,886344 * u3 + 56,136743 * u2 + 146,486415 * u + 227,967782)
baseLevel3 = n - round (14.959815 * u3 - 253.661725 * u2 + 1584.713376 * u - 3060.691342)

4.2 Blockstruktur

Der Algorithmus ist in Form einer Folge von fünf Ereignisblöcken aufgebaut , wobei jedes Ereignis der Ausführung eines bestimmten Teils der Lösung des Problems zugeordnet ist. Die Verarbeitungsalgorithmen in jedem Block unterscheiden sich voneinander. Nur drei der fünf Blöcke dienen zur Bildung einer sequentiellen Lösungskette, und die verbleibenden zwei Blöcke sind vorbereitend. Die Wahl der Blocknummer, ab der die Berechnungen beginnen, hängt vom Wert von n und von den Ergebnissen des Vergleichs der Zusammensetzungsgröße k mit den Werten von baseLeve2 und baseLevel3 ab . Eine Ausnahme bildet das Intervall der Werte n = (7, ..., 99) , das aufgrund der Besonderheiten des Algorithmusverhaltens in diesem Abschnitt als "turbulente Zone" bezeichnet werden kann. Für die Werte n = (7, ..., 49) beginnen die Berechnungen unabhängig von der Größe der Zusammensetzung nach der Eingabe und Überwachung der Daten ab dem 4. Block. Für Werte n = (50, ..., 99) beginnen die Berechnungen je nach Größe der Komposition entweder ab dem zweiten Block oder ab dem vierten. Wie oben erwähnt, werden bei jedem Schritt zur Lösung des Problems nur die Positionen in der Linie berücksichtigt, die nicht in die von den zuvor eingerichteten Königinnen geschaffene Beschränkungszone fallen. Es sind diese Positionen, die als frei bezeichnet werden .
Beschreiben wir kurz, welche Berechnungen in jedem dieser fünf Programmblöcke durchgeführt werden.

4.3 Beginn des Algorithmus

Die Daten werden eingegeben und die Zusammensetzung auf Richtigkeit überprüft. Bei jedem Überprüfungsschritt werden die Zellen der Steuerfelder geändert. Die Anzahl der korrekt installierten Königinnen wird gezählt. Wenn die Komposition keine Fehler enthält, wird die Lösung fortgesetzt, andernfalls wird eine Fehlermeldung angezeigt. Nach Abschluss der Überprüfung werden Kopien der Haupt-Arrays für deren Wiederverwendung auf dieser Ebene erstellt. Danach wird die Steuerung auf Block 1 übertragen .

4.4 Block 1

Der Beginn der Bildung des Suchzweigs. Wir betrachten k Damen auf einem Schachbrett als Startposition. Es ist erforderlich, diese Komposition fortzusetzen und die Damen auf ein Schachbrett zu legen, bis ihre Gesamtzahl gleich baseLevel2 ist . Der hier verwendete Algorithmus heißt randSet & randSet . Dies liegt an der Tatsache, dass wir hier ständig zwei zufällige Listen von Indizes vergleichen, um Paare zu suchen, die frei von den entsprechenden diagonalen Beschränkungen sind. Dazu werden folgende Aktionen ausgeführt:

a) Es werden zwei Listen gebildet: eine Liste freier Zeilenindizes und eine Liste freier Spaltenindizes;

b) zufällige Neuordnung von Zahlen in jeder dieser Listen;

c) In einer Schleife wird jedes aufeinanderfolgende Wertepaar (i, j) , bei dem Index (i) aus der Liste der freien Zeilenindizes und Index (j) aus der Liste der freien Spaltenindizes ausgewählt wird, als mögliche Königinposition betrachtet und geprüft, ob dies der Fall ist Position im Projektionsbereich von diagonalen Ausnahmen.

Wenn die Regel der diagonalen Ausnahmen nicht verletzt wird, gilt die Position als korrekt und die Dame wird an diese Position gesetzt. Danach wird der Zähler um die Anzahl der korrekt installierten Königinnen erhöht und die entsprechenden Zellen der Steuerfelder werden geändert. Fällt die Position (i, j) in die Zone der diagonalen Beschränkungen, die durch die zuvor festgelegten Königinnen gebildet werden, so ändert sich nichts und der Übergang zur Berücksichtigung des nächsten Wertepaares findet statt.

Wenn der Vergleichszyklus aller Paare der Liste abgeschlossen ist, wird basierend auf den verbleibenden Indizes, die sich in der diagonalen Ausschlusszone befinden, erneut eine Liste der Indizes der verbleibenden freien Zeilen und freien Spalten gebildet, und dieser Vorgang wird wiederholt, bis die Gesamtzahl der korrekt platzierten Königinnen (totPos ) wird nicht gleich dem Grenzwert von baseLevel2 sein oder diesen überschreiten. Sobald diese Bedingung erfüllt ist, wird die Steuerung auf Block 2 übertragen . Wenn sich als Ergebnis der Suche nach einer Lösung herausstellt, dass aus der gesamten Liste der Indizes der verbleibenden freien Zeilen und freien Spalten keines der Paare für die Position der Königin geeignet ist, werden in diesem Fall die ursprünglichen Werte der Steuerfelder basierend auf zuvor erzeugten Kopien wiederhergestellt , und die Steuerung wird zum erneuten Zählen an den Anfang von Block 1 übertragen .

4.5 Block 2

Dieser Block dient als Vorbereitungsstufe für den Übergang zu Block-3 . Auf dieser Ebene ist die Anzahl der verbleibenden freien Leitungen ( freeRows ) deutlich geringer als n . Auf diese Weise können Sie Ereignisse von der ursprünglichen Matrix der Größe nxn auf eine Matrix der kleineren Größe L übertragen (1: freeRows, 1: freeRows) . Darüber hinaus werden basierend auf Informationen über die verbleibenden freien Zeilen und freien Spalten in der ursprünglichen Lösungsmatrix Nullen in die entsprechenden Zellen des Arrays L geschrieben , was anzeigt, dass diese Zellen frei sind. Bei diesem "Projektions" -Übergang bleibt die Entsprechung der Zeilen- und Spaltenindizes der neuen Matrix mit den entsprechenden Indizes der ursprünglichen Matrix erhalten. Es ist wichtig anzumerken, dass, obwohl sich bei der Lösung dieses Problems alle Ereignisse auf der ursprünglichen Matrix der Größe nxn entfalten und eine solche Matrix der Hauptaktionsbereich ist, diese Matrix in Wirklichkeit nicht erstellt wird und nur Kontrollfelder zur Berücksichtigung der Zeilenindizes A (1: n) und Spalten B (1: n) dieser Matrix.

In diesem Block werden neben dem L-Array auch zwei Arbeits-Arrays rAr (1: freeRows) und tAr (1: freeRows) gebildet, um die entsprechenden Indizes der Steuer-Arrays D1 und D2 abzuspeichern . Dies liegt an der Tatsache, dass wir, wenn wir die nächste Dame in der Zelle (i, j) der anfänglichen Matrix der Größe nxn installieren , danach die Zellen des Arrays L ausschließen müssen, die in die Projektionszone der diagonalen Ausnahmen des ursprünglichen "großen" Arrays fallen. Da die Steuerung von diagonalen Beschränkungen nur innerhalb der ursprünglichen Matrix der Größe nxn ausgeführt wird , können wir durch das Vorhandensein von Arbeitsarrays rAr und tAr die Korrespondenz aufrechterhalten und verbotene Zellen in die Grenzen von Array L übersetzen. Dies vereinfacht die Abrechnung ausgeschlossener Positionen erheblich.
Nach Abschluss der Vorarbeiten in diesem Block werden Kopien der Haupt-Arrays zur Wiederverwendung auf dieser Ebene erstellt, und die Steuerung wird an Block 3 übertragen .

4.6 Block 3

In diesem Block wird die Bildung des Lösungssuchzweigs auf der Grundlage der im vorherigen Block vorbereiteten Daten fortgesetzt. Die Anzahl der Zeilen, in denen die Damen richtig eingestellt sind, ist gleich oder größer als baseLevel-2 . Sie müssen mit der Auswahl fortfahren, bis die Anzahl der installierten Königinnen gleich baseLevel-3 ist . Hier verwenden wir den Rand & Rand- Lösungssuchalgorithmus, d.h. Um die Position einer Dame zu bilden, werden anstelle einer Liste freier Indizes nur zwei Indizes verwendet, ein zufälliger Indexwert einer freien Zeile und ein zufälliger Indexwert einer freien Position in dieser Zeile. Dieser Vorgang wird zyklisch wiederholt, bis die Gesamtzahl der platzierten Königinnen dem Wert von baseLevel-3 entspricht . Sobald diese Bedingung erfüllt ist, wird die Steuerung auf Block 4 übertragen . Wenn sich als Ergebnis von Berechnungen herausstellt, dass der Suchzweig eine Sackgasse ist, wird dieser Abschnitt der Suchzweigbildung geschlossen und kehrt zum Anfang von Block 3 zurück , von wo aus die Berechnungen erneut wiederholt werden. Hierzu werden die Anfangswerte aller Control Arrays wiederhergestellt.

4.7 Block 4

In diesem Block werden Daten für die Übertragung der Steuerung an Block 5 vorbereitet. In diesem Schritt ist die Anzahl der freien Leitungen ( nRow ) nach Abschluss der Prozedur in Block-3 noch geringer geworden. Daher ist es auch vorteilhaft, Ereignisse von einem größeren Array in ein kleineres Array zu übersetzen. Dieser Ansatz gibt uns die Möglichkeit, die erforderlichen Eigenschaften für die verbleibenden Leitungen, die wir in dieser Phase benötigen, schnell zu bestimmen. Von besonderer Bedeutung ist die Tatsache, dass es auf der Basis eines solchen Arrays möglich ist, die Aussichten des Suchzweigs für viele weitere Schritte vorherzusagen, ohne die Berechnungen abschließen zu müssen. Der Zustand ist recht einfach. Wenn sich herausstellt, dass es unter den verbleibenden freien Zeilen eine Zeile gibt, in der keine freie Position vorhanden ist, wird der betreffende Suchzweig geschlossen und die Steuerung auf einen der Blöcke der unteren Ebene übertragen. Die hier durchgeführten vorbereitenden Maßnahmen ähneln weitgehend denen in Block 2 . Basierend auf den ursprünglichen Indizes freier Zeilen und freier Spalten wird ein neues zweidimensionales Array gebildet, dessen Nullwerte freien Positionen in der ursprünglichen Lösungsmatrix entsprechen. Außerdem wird in diesem Block ein spezielles Array E (1: nRow, 1: nRow) erstellt, anhand dessen Sie die Anzahl der freien Positionen in den verbleibenden freien Zeilen bestimmen können, die geschlossen werden, wenn Sie die Position (i, j) auswählen , in die die Dame gesetzt werden soll Quellmatrix. Vor dem Übertragen der Steuerung auf Block 5 werden die folgenden Aktionen ausgeführt:

a) die Anzahl der offenen Stellen in allen verbleibenden Zeilen wird bestimmt,

b) ein Array der Summe der freien Positionen für die betrachteten Linien in aufsteigender Reihenfolge sortiert wird,

c) wenn alle verbleibenden freien Linien freie Positionen haben (d. h. der Minimalwert in dieser Rangliste ist von 0 verschieden), wird die Steuerung zu Block 5 übertragen.

Wenn sich herausstellt, dass in einer der verbleibenden Zeilen keine freie Position vorhanden ist, werden die erforderlichen Arrays basierend auf den gespeicherten Kopien wiederhergestellt, und die Steuerung wird abhängig von den Parametern der Aufgabe auf eine der Basisebenen übertragen.

d) Sicherungskopien aller Steuerfelder für diese 4. Ebene werden erstellt.

4.8 Block 5

Diese Phase ist abgeschlossen, und hier wird die Bildung des Suchzweigs „ausgewogener“ und „rationaler“ durchgeführt. Dies ist die "letzte Meile", es bleiben nur noch wenige freie Leitungen. Gleichzeitig ist dies der schwierigste Teil. Alle Fehler, die möglicherweise in den vorherigen Phasen der Bildung des Zweigs der Suche nach einer Lösung begangen wurden, werden hier zusammengefasst angezeigt - in Form des Fehlens einer freien Position in der Zeile.

Der Algorithmus dieses Blocks wird auf der Basis von zwei verschachtelten Schleifen ausgeführt, in denen die dritte Schleife ausgeführt wird. Ein Merkmal des dritten Zyklus ist, dass er wiederholt werden kann, ohne die Parameter von zwei externen Zyklen zu ändern. Dies passiert, wenn der generierte Suchzweig blockiert ist. Die Anzahl solcher Wiederholungen überschreitet nicht den Grenzwert von repeatBound , dessen optimaler Wert auf der Basis von Computerexperimenten ermittelt wurde.

Der äußere Schleifenindex ist mit einer sequentiellen Auswahl von Zeilenindizes verbunden, die nach Berechnungen auf der dritten Basisebene frei blieben. Dies geschieht auf der Grundlage einer zuvor nach der Anzahl der freien Positionen in der Zeile geordneten Liste von Zeilen. Die Auswahl beginnt mit einer Zeile mit einer Mindestanzahl von freien Positionen und wird dann in nachfolgenden Schritten in aufsteigender Reihenfolge durchgeführt. Innerhalb dieses Zyklus wird ein zweiter Zyklus gebildet, dessen Index die Indizes aller freien Positionen in der betreffenden Zeile durchläuft. Der Zweck des ersten Zyklus besteht nur darin, den Index einer der freien Zeilen auf dieser Ebene auszuwählen. Dementsprechend besteht der Zweck des zweiten Zyklus darin, nur eine freie Position innerhalb der betrachteten Linie auszuwählen. Diese Aktionen finden nur auf der dritten Grundstufe statt. Nach dieser Auswahl wird die Anzahl der installierten Königinnen erhöht und die entsprechenden Zellen aller Steuerfelder werden geändert. Ferner wird die Steuerung innerhalb eines verschachtelten (dritten) Zyklus übertragen, dessen Aktivitätszone bereits alle verbleibenden freien Leitungen enthält. Innerhalb dieses Zyklus werden die Auswahl des Zeilenindex und die Auswahl einer freien Position in dieser Zeile basierend auf den folgenden Regeln durchgeführt:

a) Wählen Sie eine freie Leitung . Alle verbleibenden freien Zeilen werden berücksichtigt, und die Anzahl der freien Positionen wird in jeder Zeile bestimmt. Die Zeile wird ausgewählt, für die die Anzahl der freien Positionen minimal ist. Dies minimiert die Risiken, die mit der Möglichkeit verbunden sind, die letzten vakanten Positionen in einigen der verbleibenden Linien, für die der Staat minimal und kritisch in Bezug auf die Anzahl der vakanten Positionen ist , auszuschließen ( Mindestrisikoregel ). Im Übrigen beginnt der Index des ersten Zyklus in diesem fünften Block mit einer sequentiellen Auswahl von Zeilen mit einem Mindestwert für die Anzahl der freien Positionen in einer Zeile. Wenn sich in einem Schritt herausstellt, dass die beiden Zeilen die gleiche Mindestanzahl an freien Positionen haben, wird der Index einer der beiden Positionen, die in der Rangliste an erster Stelle stehen, zufällig ausgewählt. Wenn die Anzahl der Zeilen mit der gleichen Mindestanzahl an freien Positionen mehr als zwei beträgt, wird der Index einer der drei Positionen, die an erster Stelle in der Rangliste aufgeführt sind, zufällig ausgewählt.

b) Auswahl einer freien Position in einer Reihe .Aus der Liste aller vakanten Positionen in der betreffenden Zeile wird eine ausgewählt, die den vakanten Positionen in allen verbleibenden Zeilen nur minimalen Schaden zufügt. Dies geschieht auf der Grundlage des zuvor gebildeten Arrays E. Mit "minimaler Beschädigung" ist die Auswahl einer solchen Position in einer bestimmten Zeile gemeint, die die geringste Menge an freien Positionen in allen verbleibenden Zeilen ausschließt ( Regel für minimale Beschädigung)) Wenn sich herausstellt, dass zwei oder mehr freie Positionen in einer Reihe gemäß dem Schadenskriterium die gleichen Mindestwerte aufweisen, wird der Index einer der beiden Positionen, die zuerst in der Liste aufgeführt sind, zufällig ausgewählt. Wenn Sie eine Position auswählen, die die Mindestanzahl an freien Positionen in den verbleibenden Zeilen ausschließt, wird der mit der Position der Königin in dieser Position verbundene „Schaden“ minimiert. Die Verwendung dieser beiden Regeln ermöglicht eine rationellere Ressourcennutzung bei jedem Schritt der Bildung eines Suchzweigs. Dies verringert das Risiko erheblich und erhöht die Wahrscheinlichkeit, eine beliebige Zusammensetzung zu einer vollständigen Lösung zu wählen, wenn die fragliche Zusammensetzung eine Lösung aufweist. Wenn sich bei einem Lösungsschritt herausstellt, dass in einer der verbleibenden zu berücksichtigenden Zeilen keine offenen Stellen vorhanden sind, wird dieser Suchzweig geschlossen. In diesem Fall,Auf der Grundlage von Sicherungen werden alle Steuerfelder wiederhergestellt, und wenn der Zähler für die Anzahl der Wiederholungen den Grenzwert nicht überschreitetrepeatBoundDann wird, ohne die Indizes des ersten und des zweiten externen Zyklus zu ändern, die Arbeit des dritten verschachtelten Zyklus erneut wiederholt. Dies ist darauf zurückzuführen, dass wir in Fällen, in denen die Mindestwerte der relevanten Kriterien übereinstimmten, eine zufällige Auswahl getroffen haben. Durch die Neugestaltung des Suchzweigs unter den gleichen Bedingungen wie auf der Basisebene können die auf dieser Ebene vorhandenen „Startressourcen“ effizienter genutzt werden. Die Anzahl der wiederholten Starts des dritten verschachtelten Zyklus ist begrenzt, und wenn der Grenzwert überschritten wird, wird der Betrieb dieses Zyklus unterbrochen. Danach werden die Werte der Steuerfelder wiederhergestellt, und die Steuerung wird in den Zyklus der dritten Basisebene übertragen, um zum nächsten Indexwert zu gelangen. Diese Prozedur wird zyklisch wiederholt, bis eine vollständige Lösung erhalten wird, oder es stellt sich heraus, dassdass wir alle freien Zeilen und alle freien Positionen in diesen Zeilen auf dieser Basisebene verwendet haben. In diesem Fall kehrt man in Abhängigkeit von der Gesamtzahl der wiederholten Berechnungen auf verschiedenen Basisebenen und unter Berücksichtigung der Größe der Entscheidungsmatrix und der Größe der Zusammensetzung zu einer der niedrigeren Ebenen für wiederholte Berechnungen zurück, oder es wird beurteilt, dass die fragliche Zusammensetzung nicht sein kann ausgerüstet, um Lösung zu vervollständigen. In dem Programm wird, um die Gesamtzeit der Rechnung zu begrenzen, das Verfahren akzeptiertoder es wird entschieden, dass die fragliche Komposition erst nach einer vollständigen Entscheidung vervollständigt werden kann. In dem Programm wird, um die Gesamtzeit der Rechnung zu begrenzen, das Verfahren akzeptiertoder es wird entschieden, dass die fragliche Komposition erst nach einer vollständigen Entscheidung vervollständigt werden kann. In dem Programm wird, um die Gesamtzeit der Rechnung zu begrenzen, das Verfahren akzeptiertDie Rückverfolgung kann , unabhängig davon, auf welche der vorherigen Ebenen die Rückgabe erfolgt, nur bis zu totSimBound- Zeiten durchgeführt werden. Dieser Grenzwert wird auf der Grundlage von Berechnungsexperimenten für verschiedene Werte von n ausgewählt.

5. Analyse der Wirksamkeit von Auswahlalgorithmen

Die Effizienz des randSet & randSet-Algorithmus . Um die Fähigkeiten dieses Algorithmus zu analysieren, wurde ein Computerexperiment durchgeführt, das darin bestand , Königinnen in der Lösungsmatrix basierend auf dem randSet & randSet- Modell zu platzieren, solange diese Möglichkeit besteht. Sobald der Suchzweig eine Sackgasse erreichte oder eine vollständige Lösung erhalten wurde, wurden die Zusammensetzungsgröße, die Lösungszeit festgelegt und der Test erneut wiederholt. Computerexperimente wurden für die gesamte Basisliste von n Werten durchgeführt . Die Anzahl der wiederholten Tests für die Werte n = (30, 40, ..., 90, 100, 200, 300, 500, 800, 1000) betrug eine Million , für die übrigen Werte die Anzahl der Tests mit zunehmendem nEine Analyse der Ergebnisse von Computerexperimenten erlaubt es uns, die folgenden Schlussfolgerungen zu ziehen:

a) Als Ergebnis nur des ersten Zyklus der randSet & randSet-Prozedur sind durchschnittlich etwa 60% aller Königinnen korrekt platziert. Für n = 100 beträgt die Anzahl der korrekt platzierten Königinnen 60,05%. Mit zunehmendem Wert von n nimmt dieser Wert allmählich ab und für n = 10 ⁷ beträgt er 59,97%.

b) Das Histogramm der Verteilung der Längenwerte der erhaltenen Zusammensetzungen hat unabhängig von der Größe der Entscheidungsmatrix n die gleiche Form. Darüber hinaus haben sie alle ein charakteristisches Merkmal - die linke Seite der Verteilung (zum Modalwert) unterscheidet sich von der rechten Seite. Abbildung 2 zeigt als Beispiel das entsprechende Histogramm für


Abb.2. Ein Histogramm der Verteilung von Lösungen unterschiedlicher Länge für das randSet & randSet-Modell ( n = 100, Stichprobengröße = 10 ⁶ ).

n = 100. Es scheint, dass das Histogramm aus der Häufigkeitsverteilung von zwei verschiedenen Ereignissen gewonnen wird, da die Häufigkeit des Auftretens von Ereignissen im linken und rechten Teil der Verteilung unterschiedlich ist. Um diese Verteilung zu beschreiben, ist es am wahrscheinlichsten, zwei Funktionen der Dichte der Normalverteilung zu verwenden, von denen eine das Intervall bis zum Modalwert und die andere - das Intervall nach dem Modalwert - abdeckt.

c) Der Durchschnittswert der Anzahl der Königinnen ( qMean ), die in der auf diesem Algorithmus basierenden Entscheidungsmatrix festgelegt werden können, steigt mit n. Wie aus Fig. 3 ersichtlich ist, wo ein Graph der Abhängigkeit des qMean / n- Verhältnisses von der Matrixgröße n dargestellt ist , nimmt dieses Verhältnis mit einer Zunahme der Matrixgröße zu. Zum Beispiel

Abb.3. Die Abhängigkeit des Verhältnisses qMean / n vom Wert von n für verschiedene Größen der Lösungsmatrix. Das Modell ist randSet & randSet , qMean ist der Durchschnittswert der Länge der Lösung.

Wenn für eine 100x100- Matrix der Positionsauswahlalgorithmus randSet & randSet "ohne anzuhalten" erlaubt, Königinnen auf durchschnittlich 89 Zeilen zu platzieren, erhöht sich für eine 1000x1000- Matrix die Anzahl solcher Zeilen im Durchschnitt auf 967.

d) Basierend auf dem randSet & randSet-Algorithmus können Sie den vollständigen Wert erhalten Als Lösung ist die „Produktivität“ dieses Ansatzes jedoch äußerst gering. Wie aus Figur 4 ersichtlich ist, z


Abb.4. Die Abnahme der Wahrscheinlichkeit, im randSet & randSet-Modell eine vollständige Lösung zu erhalten, mit einer Zunahme von n .

Bei Werten von n = 7 beträgt die Wahrscheinlichkeit, eine vollständige Lösung zu erhalten, 0,057 . Ferner nimmt mit einer Zunahme von n die Wahrscheinlichkeit, eine vollständige Lösung zu erhalten, schnell ab und nähert sich asymptotisch Null. Beginnend mit den Werten n = 48, ist die Wahrscheinlichkeit eine Komplettlösung in der Größenordnung von 10 zu erhalten ^-6 . Nach dem Schwellenwert n = 70 wurde für die nachfolgenden Werte von n keine einzige vollständige Lösung erhalten (mit einer Anzahl von Tests von einer Million ).

e) ModellrandSet & randSet bilden sehr schnell Suchzweige . Für n = 1000 beträgt die durchschnittliche Zeit zum Erhalten der Zusammensetzung 0,0015 Sekunden. Die durchschnittliche Länge von Kompositionen beträgt 967. Dementsprechend beträgt ^die durchschnittliche Zeit für n = 10 ⁶ 2,6754 Sekunden bei einer durchschnittlichen Länge von Kompositionen von 999793.

f) Mit Ausnahme eines kleinen Intervalls n <= 70, zu dem das randSet & randSet-Modell in sehr seltenen Fällen führen kann vollständige lösung, in allen anderen fällen endet der entscheidungszweig mit der bildung einer negativen zusammensetzung, die erst mit einer vollständigen lösung abgeschlossen werden kann. Also der randSet & randSet AlgorithmusEs hat einen wichtigen Vorteil - die hohe Geschwindigkeit der Bildung des Suchzweigs und ein wesentlicher Nachteil besteht darin, dass dieser Algorithmus zur Bildung von Zusammensetzungen führt, wenn die Größe der Zusammensetzung einen bestimmten Schwellenwert überschreitet, der erst zu einer vollständigen Lösung abgeschlossen werden kann. Um diesen Nachteil zu beseitigen , stoppen wir die Bildung des Suchzweigs, wenn der Schwellenwert baseLevel-2 erreicht ist .

Die Effizienz des Rand & Rand- Algorithmus . Um die Fähigkeiten des Rand & Rand- Algorithmus zu bestimmen , wurde eine ziemlich detaillierte Computersimulation für eine Grundliste von n Werten durchgeführt . Wie beim randSet & randSet ModellIn den meisten Fällen betrug die Anzahl der erneuten Tests eine Million . Bei anderen Werten verringerte sich die Anzahl der Tests allmählich von 100.000 auf 100.

Beide Algorithmen basieren auf dem Prinzip der Zufallsauswahl. Daher ist zu erwarten, dass die hier gezogenen Schlussfolgerungen im Wesentlichen mit den für das randSet & randSet-Modell formulierten Schlussfolgerungen übereinstimmen . Es gibt jedoch einen grundlegenden Unterschied zwischen ihnen und er besteht aus Folgendem:

a) Das rand & rand- Modell funktioniert nicht so "hart" wie das randSet & randSet-Modell . Wenn wir von einem „Index rationaler Nutzung der gebotenen Möglichkeiten“ sprechen, dem rand & rand- ModellBei jedem Schritt werden Ressourcen rationeller eingesetzt. Dies führt dazu, dass beispielsweise bei n = 30 die Wahrscheinlichkeit, in diesem Modell eine vollständige Lösung von 0,00170 zu erhalten, 15-mal größer ist als der ähnliche Wert von 0,00011 für das randSet & randSet-Modell . Außerdem bleibt hier bis zum Schwellwert n = 370 die Wahrscheinlichkeit bestehen, in einer Million Tests mindestens eine vollständige Lösung zu erhalten. Nach diesem Schwellenwert wurde für nachfolgende Werte von n mit einer Anzahl von Tests von einer Million keine vollständige Lösung auf der Basis des Rand & Rand- Modells erhalten .

b) Dieser Algorithmus ist viel langsamer als der Algorithmus randSet & randSet . Wenn fürn = 1000, um eine Komposition der Größe 967 zu generieren. Die durchschnittliche Zeit, um eine Komposition zu erhalten, beträgt 0,0497 Sekunden. Dies sind 33 Sekunden mehr als der entsprechende Wert von 0,0015 für das randSet- und randSet-Modell .

Der Grund für die Unterschiede zwischen zwei im Wesentlichen ähnlichen Methoden der Zufallsauswahl liegt darin, dass im randSet & randSet-Modell zur Beschleunigung der Berechnungen nicht bei jedem Schritt eine Zufallsauswahl aus der verbleibenden Liste durchgeführt wird. Stattdessen wird ein Indexpaar nacheinander aus zwei Listen ausgewählt, deren Elemente nach dem Zufallsprinzip neu angeordnet wurden. Eine solche Auswahl ist nicht in vollem Umfang zufällig, passt jedoch gut zur Logik des Problems und ermöglicht es Ihnen, schnell zu zählen.

Zur visuellen Demonstration der Funktionsweise des rand & rand- AlgorithmusEs wurde folgendes Experiment durchgeführt:

a) Für ein Schachbrett der Größe 100x100Nach jedem Schritt der Position der Königin in einer beliebigen Zeile wurde die Anzahl der freien Positionen in jeder der verbleibenden freien Zeilen bestimmt. So erhielten wir nach jedem Schritt der Problemlösung eine Liste der freien Zeilen und eine entsprechende Liste der Anzahl der freien Positionen in diesen Zeilen. Dies ermöglichte es, ein Diagramm zu erstellen, in dem die Indizes der Spalten der fraglichen Matrix entlang der Abszissenachse und die Anzahl der verbleibenden freien Positionen entlang der Ordinatenachse aufgetragen sind. Zum Vergleich wurden die Berechnungen auch für das Modell der sequentiellen Positionsauswahl durchgeführt. Mit sequentieller Auswahl ist das Folgende gemeint. Es wird die erste Zeile berücksichtigt, in der die erste freie Position in der Liste ausgewählt wird. Dann wird die zweite Zeile berücksichtigt, in der auch die erste freie Position in der Liste usw. ausgewählt wird. In den Abbildungen 5 und 6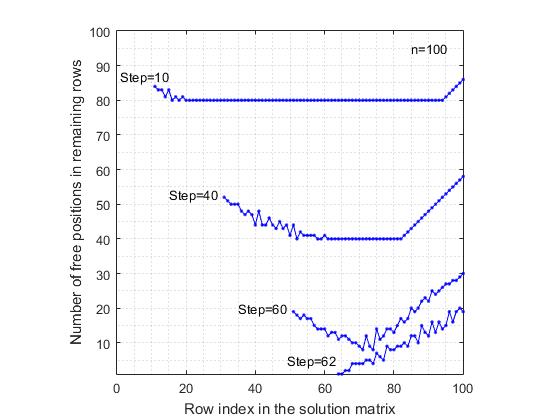


Abb.5. Reduzieren Sie die Anzahl der freien Positionen in den verbleibenden freien Linien nach der Platzierung der Königinnen. Sequenziell regelmäßige Positionsauswahl.

Die Ergebnisse, die den betrachteten Modellen entsprechen, werden vorgestellt. Zur Verdeutlichung zeigt das Diagramm die Ergebnisse erst nach den Schritten (10, 40, 60). Für das Modell der sequentiellen Auswahl von Positionen ist die letzte die Grafik nach dem 62. Schritt, da der Suchzweig aufgrund des Fehlens einer freien Position in der 63. Zeile endet. Andererseits wird im rand & rand- Modell die letzte Grafik nach dem 70. Schritt des Platzierens der Königin dargestellt, obwohl hier die durchschnittliche Anzahl der korrekt platzierten Königinnen 89 erreicht, was 26 Schritte mehr ist als im sequentiellen Modell. Eine seltsame Ansicht der Graphen im rand & rand- Modellaufgrund der Tatsache, dass der Zeilenindex zufällig aus den verbleibenden freien Zeilen ausgewählt wird und sie daher zufällig in der Lösungsmatrix verstreut sind. Ein Vergleich dieser beiden Zahlen zeigt, dass im sequentiellen Modell der Positionsauswahl der Variabilitätsbereich der Anzahl der freien Positionen höher ist als im rand & rand- Modell . Dies liegt an der Tatsache, dass bei regelmäßiger Auswahl diagonale Beschränkungen freie Positionen in den verbleibenden Zeilen ungleichmäßig ausschließen, was dazu führt, dass in einigen Zeilen die Rate der Verringerung der Anzahl freier Positionen höher ist als in anderen Zeilen.


Abb.6. Reduzieren Sie die Anzahl der freien Positionen in den verbleibenden freien Linien nach der Platzierung der Königinnen. Das Positionierungsmodell ist rand & rand .

Im Gegensatz dazu werden bei zufälliger Auswahl des freien Zeilenindex und des freien Spaltenindex die Positionen der Dame gleichmäßig über den "Bereich" der Entscheidungsmatrix verteilt, wodurch die "durchschnittliche" Verringerungsrate der Anzahl freier Positionen in den verbleibenden Zeilen verringert wird. Unter Berücksichtigung der Funktionen des rand & rand- Algorithmus wird dieser im Programm verwendet, um die Bildung des Lösungssuchzweigs fortzusetzen, bis die baseLevel-3- Ebene erreicht ist .

Es ist zu beachten, dass auch wenn die Auswahlalgorithmen ( randSet & randSet, rand & rand) nicht so effektiv wäre, müssten wir bei der Entwicklung des Algorithmus noch eine andere Zufallsauswahlmethode anwenden. Dies ist auf die Aussage des n-Queens-Completion-Problems zurückzuführen . Wenn wir uns vorstellen, dass es einen bestimmten optimalen Algorithmus gibt, der das Problem löst, dann erhält ein solcher Algorithmus am Eingang immer eine bestimmte zufällige Menge von Zeilen- und Spaltenindizes. Jedes Mal wird es einen neuen zufälligen Satz von Zeilen- und Spaltenindizes aus einer Vielzahl von Möglichkeiten geben. Um den Algorithmus in einer solchen Vielfalt von Zufallszusammensetzungen "aufnehmen" zu können, muss der Algorithmus selbst auf der Basis einer Zufallsauswahl aufgebaut werden. Matching sollte wie ein Schlüssel zum Schloss sein . Konstruieren wir den Algorithmus nach diesem Prinzip, so ergibt sich eine beliebige konsistente Zusammensetzung ausk Königinnen werden als Ausgangsposition im Entscheidungssuchzyklus betrachtet. Außerdem wird das Ziel nur darin bestehen, den Zweig der Suche nach einer Lösung fortzusetzen, bis eine Lösung für eine gegebene Zusammensetzung gefunden wird, oder es wird bewiesen, dass eine solche Lösung nicht existiert.

6. Ein Beispiel für die Verwendung der Minimalrisikoregel (n = 100)

In der Anfangsphase der Lösungsfindung ist die Auswahl des Index der freien Zeile oder des Index der Position in dieser Zeile nicht schwerwiegend, wenn die Anzahl der freien Positionen in den Zeilen nicht kritisch ist. Wenn jedoch in der letzten Phase die Anzahl der freien Positionen in einigen Zeilen 1 oder 2 beträgt, sollten Sie in diesem Fall einen anderen Auswahlalgorithmus auswählen. Auf dieser Ebene funktionieren die Zufallsauswahlalgorithmen randSet & randSet und rand & rand nicht mehr.

Der Grund, warum Zufallsauswahlalgorithmen nicht funktionieren, kann anhand des folgenden einfachen Beispiels erklärt werden. Lassen Sie in einem Schritt das Problem für einen beliebigen Wert von n in den verbleibenden Zeilen i ₁ , i ₂ , ..., i _k lösenDie Anzahl der offenen Stellen (in Klammern angegeben) beträgt: i ₁ (1), i ₂ (2), i ₃ (4), i ₄ (5), i ₅ (3), i ₆ (4) usw. Wenn Sie nach dem Zufallsprinzip eine Zeile auswählen, jedoch nicht die Zeile i ₁ , in der nur eine freie Position vorhanden ist, kann dies zu einer Risikosituation führen, wenn diagonale Verbote in Bezug auf die Position der Dame in der ausgewählten Zeile zur Schließung der einzigen freien Position in der Zeile führen können i ₁ , was die Lösung zum Stillstand bringt. Von allen Zeilen i ₁ , i ₂ , ..., i _kAm anfälligsten und empfindlichsten für die Auswahl des Zeilenindex ist Zeile i ₁ . In solchen Situationen sollten Sie zuerst die Zeile auswählen, deren Status am kritischsten ist und ein Risiko für die Lösung des Problems darstellt. In der letzten Phase der Problemlösung muss daher bei jedem Schritt die Position der Linie auf der Grundlage eines einfachen Algorithmus mit minimalem Risiko ausgewählt werden.

Betrachten wir der Klarheit halber als Beispiel für eine 100 x 100- Matrix die letzte Stufe bei der Bildung einer echten Lösung nach dem 88. Schritt. Bis zum Abschluss der Aufgabe blieben 12 freie Zeilen, für die jeweils die Anzahl der freien Positionen gefunden wurde (die Zeilen sind in aufsteigender Reihenfolge der Anzahl der freien Positionen angeordnet):Schritt 89 - 25 (1), 12 (2), 22 (2), 82 (2), 88 (2), 7 (3), 64 (3), 3 (4), 76 (4), 91 (4), 4 (5), 96 (5) - gibt den Index einer freien Zeile und in Klammern die Anzahl der freien Positionen in dieser Zeile an. Gemäß der minimalen Risikoregel wird im 89. Schritt der Problemlösung die Zeile 25 ausgewählt und die eine freie Position, die sich darin befindet. Als Ergebnis der Nachzählung haben wir noch 11 freie Zeilen: Schritt-90 - 7 (2), 12 (2), 22 (2), 82 (2), 88 (2), 3 (3), 64 (3), 76 (3), 4 (4), 91 (4), 96 (4).Wie Sie sehen können, ist die Anzahl der freien Positionen in den ersten fünf Zeilen gleich und gleich 2. Daher wird der Index einer der ersten drei Zeilen zufällig ausgewählt. In diesem Fall wurde die 12. Reihe ausgewählt und die Position der beiden verbleibenden in dieser Reihe, was zu minimalem Schaden führt. So haben wir im 91. Schritt der Lösungsbildung 10 freie Linien: Schritt-91 - 22 (1), 3 (2), 7 (2), 82 (2), 88 (2), 64 (3) 76 (3), 91 (3), 4 (4), 96 (4) . In diesem Schritt wird Zeile 22 ausgewählt und die eine freie Position, die sich darin befindet. In ähnlicher Weise wurde die folgende Abfolge von Entscheidungen getroffen (Tabelle 1). Die Indizes der ausgewählten Zeilen sind fett gedruckt.

In diesem speziellen Beispiel gab es in 11 von 12 Fällen eine Situation, in der in der Liste der verbleibenden freien Zeilen mindestens eine Zeile vorhanden war, in der nur eine freie Position vorhanden war. Wenn wir nicht die Mindestrisikoregel anwenden, können wir nicht bis zum Ende kommen. Da ein „falscher Zug“ bei der Auswahl eines Index einer freien Zeile zu einer Zerstörung der einzigen freien Position führen würde, die sich in einer der verbleibenden freien Zeilen befand. Dies ist der Grund, warum die Lösung in den letzten Phasen in eine Sackgasse gerät , wenn nur der Algorithmus randSet x randSet oder rand x rand verwendet wird , um eine vollständige Lösung zu erhalten.
Es ist zu beachten, dass der Minimalrisiko-Algorithmus eine einfache alltägliche Bedeutung hat und häufig bei der Entscheidungsfindung verwendet wird. Zum Beispiel operiert der Arzt zuallererst den Patienten, dessen Zustand für das Leben am kritischsten ist, ebenso wie der Landwirt während einer schweren Dürre, der versucht, die Ernte zu retten, zuerst die Bereiche wässerte, die sich in dem kritischsten Zustand befinden ...

7. Analyse der Effizienz des Algorithmus

Um die Effizienz des Algorithmus für verschiedene Werte von n zu bewerten, wurde ein relativ langwieriges (in Bezug auf die Gesamtzeit) Rechenexperiment durchgeführt. Anfänglich wurde ein ziemlich schneller Algorithmus entwickelt, um Arrays von Lösungen nQueens Problem für einen beliebigen Wert von n zu erzeugen. Basierend auf diesem Programm wurden dann große Stichproben von Lösungen für eine Grundliste von n Werten gebildet. Die Größen der erhaltenen Proben von nQueens Problemlösungen für verschiedene Werte von n waren gleich: (10) - 1000, (20, 30, ..., 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10.000) - -10000, (30000, 50000, 80000) - 5000, (105, 3 * 105) - 3000, (5 * 105, 8 * 105, 106) - 1000, (3 * 106) - 300, ( 5 * 106) - 200, (10 * 106) - 100, (30 * 106) - 50, (50 * 106) - 30, (80 * 106, 100 * 106) - 20. Hier ist in Klammern eine Liste von n Werten angegeben, und ein doppelter Strich gibt die Stichprobengröße der erhaltenen Lösungen an.Danach wurden zufällige Zusammensetzungen beliebiger Größe auf der Basis jeder Probe von Lösungen gebildet. Beispielsweise wurden für jede von 10.000 Lösungen für n = 1000 100 zufällige Zusammensetzungen beliebiger Größe gebildet. Das Ergebnis war eine Probe von einer Million Songs. Da jede Zusammensetzung beliebiger Größe, die auf der Grundlage einer vorhandenen Lösung gebildet wird, mindestens einmal bis zu einer vollständigen Lösung vervollständigt werden kann, bestand die Aufgabe darin, jede Zusammensetzung von der erzeugten Probe bis zu einer vollständigen Lösung auf der Grundlage des Lösungsalgorithmus für das n-Queens-Vervollständigungsproblem zu vervollständigen . Da im betrachteten Algorithmus bei jedem Schritt die korrekte Platzierung der Dame auf dem Schachbrett überprüft wird, kann dies hier grundsätzlich nicht der Fall seinAuf der Basis jeder Probe von Lösungen wurden zufällige Zusammensetzungen beliebiger Größe gebildet. Beispielsweise wurden für jede von 10.000 Lösungen für n = 1000 100 zufällige Zusammensetzungen beliebiger Größe gebildet. Das Ergebnis war eine Probe von einer Million Songs. Da jede Zusammensetzung beliebiger Größe, die auf der Grundlage einer vorhandenen Lösung gebildet wird, mindestens einmal bis zu einer vollständigen Lösung vervollständigt werden kann, bestand die Aufgabe darin, jede Zusammensetzung von der erzeugten Probe bis zu einer vollständigen Lösung auf der Grundlage des Lösungsalgorithmus für das n-Queens-Vervollständigungsproblem zu vervollständigen . Da im betrachteten Algorithmus bei jedem Schritt die korrekte Platzierung der Dame auf dem Schachbrett überprüft wird, kann dies hier grundsätzlich nicht der Fall seinAuf der Basis jeder Probe von Lösungen wurden zufällige Zusammensetzungen beliebiger Größe gebildet. Beispielsweise wurden für jede von 10.000 Lösungen für n = 1000 100 zufällige Zusammensetzungen beliebiger Größe gebildet. Das Ergebnis war eine Probe von einer Million Songs. Da jede Zusammensetzung beliebiger Größe, die auf der Grundlage einer vorhandenen Lösung gebildet wird, mindestens einmal bis zu einer vollständigen Lösung vervollständigt werden kann, bestand die Aufgabe darin, jede Zusammensetzung von der erzeugten Probe bis zu einer vollständigen Lösung auf der Grundlage des Lösungsalgorithmus für das n-Queens-Vervollständigungsproblem zu vervollständigen . Da im betrachteten Algorithmus bei jedem Schritt die korrekte Platzierung der Dame auf dem Schachbrett überprüft wird, kann dies hier grundsätzlich nicht der Fall seinEs wurden 100 zufällige Zusammensetzungen beliebiger Größe gebildet. Das Ergebnis war eine Probe von einer Million Songs. Da jede Zusammensetzung beliebiger Größe, die auf der Grundlage einer vorhandenen Lösung gebildet wird, mindestens einmal bis zu einer vollständigen Lösung vervollständigt werden kann, bestand die Aufgabe darin, jede Zusammensetzung von der erzeugten Probe bis zu einer vollständigen Lösung auf der Grundlage des Lösungsalgorithmus für das n-Queens-Vervollständigungsproblem zu vervollständigen . Da im betrachteten Algorithmus bei jedem Schritt die korrekte Platzierung der Dame auf dem Schachbrett überprüft wird, kann dies hier grundsätzlich nicht der Fall seinEs wurden 100 zufällige Zusammensetzungen beliebiger Größe gebildet. Das Ergebnis war eine Probe von einer Million Songs. Da jede Zusammensetzung beliebiger Größe, die auf der Grundlage einer vorhandenen Lösung gebildet wird, mindestens einmal bis zu einer vollständigen Lösung vervollständigt werden kann, bestand die Aufgabe darin, jede Zusammensetzung von der erzeugten Probe bis zu einer vollständigen Lösung auf der Grundlage des Lösungsalgorithmus für das n-Queens-Vervollständigungsproblem zu vervollständigen . Da im betrachteten Algorithmus bei jedem Schritt die korrekte Platzierung der Dame auf dem Schachbrett überprüft wird, kann dies hier grundsätzlich nicht der Fall seindann bestand die Aufgabe darin, jede Komposition von der generierten Stichprobe, basierend auf dem Lösungsalgorithmus für das n-Queens-Abschlussproblem, zu einer vollständigen Lösung zu vervollständigen. Da im betrachteten Algorithmus bei jedem Schritt die korrekte Platzierung der Dame auf dem Schachbrett überprüft wird, kann dies hier grundsätzlich nicht der Fall seinAnschließend bestand die Aufgabe darin, jede Komposition von der generierten Stichprobe auf der Grundlage des Lösungsalgorithmus für das n-Queens-Abschlussproblem zu einer vollständigen Lösung zu vervollständigen. Da im betrachteten Algorithmus bei jedem Schritt die korrekte Platzierung der Dame auf dem Schachbrett überprüft wird, kann dies hier grundsätzlich nicht der Fall seinFalsch positive Entscheidungen (d. H. Falsche Entscheidungen, die wir fälschlicherweise für richtig halten). Es kann jedoch auch zu falsch-negativen Lösungen kommen - für den Fall, dass eine auf der Basis der vorhandenen Lösung gebildete Zusammensetzung vom Programm erst vervollständigt wird, wenn die Lösung vollständig ist (obwohl wir wissen, dass alle Zusammensetzungen eine Lösung haben). Bei der Durchführung eines Computerexperiments in einem derart großen Bereich von n Werten haben wir uns folgende Ziele gesetzt:

a) Bestimmung der zeitlichen Komplexität des Algorithmus,

b) Bestimmung der Wahrscheinlichkeit von falsch negativen Lösungen für verschiedene Werte von n,

c) Bestimmung der Häufigkeit, mit der das Back Tracking-Verfahren angewendet wird verschiedene Werte von n.

Die Ergebnisse eines solchen Berechnungsexperiments sind in Tabelle 2 dargestellt.

Die allgemeine Schlussfolgerung, die auf der Grundlage der erhaltenen Ergebnisse gezogen werden kann, lautet wie folgt:

a) Der Algorithmus arbeitet schnell genug. Beispielsweise beträgt die durchschnittliche Kompilierungszeit einer beliebigen Komposition für ein Schachbrett der Größe 1000 x 1000 , die auf der Grundlage von einer Million Rechenexperimenten erhalten wurde, 0,062157 Sekunden. Das heißt, wenn die Komposition eine Lösung hat, wird diese sofort nach dem Drücken der "Enter" -Taste gefunden . Die durchschnittliche Kompilierungszeit einer beliebigen Komposition für alle Werte von n im Bereich von 7 bis 30.000 überschreitet eine Sekunde nicht.

b) In jeder Probe gibt es ungefähr 10% der Zusammensetzungen, die viel mehr Zeit benötigen, um fertig zu werden. Solche Zusammensetzungen bilden im Verteilungshistogramm einen langen rechten Schwanz. Wenn wir diese 10% der Zusammensetzungen ausschließen und Berechnungen für die restlichen 90% der Lösungen durchführen, ist die Berechnungszeit ( _Mittelwert t90 ) viel kürzer. Bei einem Schachbrett von 1000 x 1000 beträgt die durchschnittliche Zählzeit beispielsweise 0,027727 Sekunden, was dem 2,24-fachen der durchschnittlichen Zeit entspricht, die auf der Grundlage der gesamten Stichprobe ermittelt wurde.

c) Für Werte von n ≤ 800 gab es in der Stichprobe von Zusammensetzungen diejenigen, die bis zu einer vollständigen Lösung nicht vervollständigt werden konnten. Dies ist falsch negativEntscheidungen. Der Algorithmus konnte diese Kompositionen innerhalb der im Programm festgelegten Grenzen, die es ermöglichten, das Back-Tracking- Verfahren bis zu 1000-mal durchzuführen , nicht vervollständigen. Sie wurden fälschlicherweise als negative Zusammensetzungen klassifiziert, d.h. diejenigen, die keine Lösung haben. Die Anzahl solcher falsch-negativen Lösungen ist unbedeutend und ihr Anteil an der Stichprobe beträgt weniger als 0,0001. Wenn n zunimmt , nimmt ferner der Anteil der falsch negativen Lösungen ab. Für alle Werte von n > 800 gab es in dieser Reihe von Rechnerexperimenten keinen einzigen Fall von falsch negativen Lösungen. Es ist jedoch offensichtlich, dass die Möglichkeit des Auftretens von falschem Negativ nicht ausgeschlossen wird, wenn die Probengröße um ein Vielfaches erhöht wirdLösungen, obwohl die Wahrscheinlichkeit eines solchen Ereignisses sehr gering sein wird.

Die zeitliche Komplexität des Algorithmus . Fig. 7 zeigt eine graphische Darstellung von Änderungen in der durchschnittlichen Aufnahmedauer von Zufallszusammensetzungen für verschiedene Werte von n .


Abb.7. Die Abhängigkeit der durchschnittlichen Erntezeit ( t ) zufälliger Zusammensetzungen von der Größe ( n ) der Entscheidungsmatrix.

Auf der Abszissenachse ist der dezimale Logarithmus des Wertes von n und auf der Ordinatenachse der um das 1000-fache erhöhte Logarithmus der mittleren Zählzeit aufgetragen. Zur Verdeutlichung zeigt die Figur auch die gepunktete Linie der Diagonale des Quadranten. Es ist zu sehen, dass die Erntezeit linear mit einer Zunahme von n zunimmt. Über den gesamten Bereich von n-Werten von 50 bis 10 ^{8 bilden die} experimentellen Zählzeiten eine gerade Linie, die mit einer relativ hohen Korrelation ( R = 0,9998 ) durch die lineare Regressionsgleichung

log (1000 * t) = - 0,628927 + 0,781568 * log (n) beschrieben wird.

Eine leichte Abweichung vom allgemeinen Trend ist nur für die Werte n = (10, ... 49) typisch , da zur Lösung des Problems nur der fünfte Berechnungsblock in diesem Bereich verwendet wird, dessen Algorithmus sich erheblich von der Funktionsweise der Algorithmen des ersten und dritten Blocks unterscheidet. In der erhaltenen Abhängigkeit ist der lineare Koeffizient ( 0,781568 ) kleiner als Eins, was dazu führt, dass mit zunehmendem n die Regressionslinie und die Diagonale des Quadranten auseinander laufen. Um den Grund für eine solche Diskrepanz anstelle der Anfangszeit klar zu erklären, betrachten wir die durchschnittliche Zeit, die für den Ort einer Dame auf einer Zeile erforderlich ist, d. H. dividiere die durchschnittliche Zählzeit durch n . Wir nennen einen solchen Indikator die reduzierte Zeit.. Wenn sich die reduzierte Zeit mit zunehmendem n nicht ändert , ist eine solche Lösung offensichtlich linear ( O (n) ). Wie aus Fig. 8 ersichtlich ist, zeigt diese eine Auftragung des Logarithmus der reduzierten Zeit


Abb.8 Die Abhängigkeit der Durchschnittszeit ( t _row ), die erforderlich ist, damit sich die Dame auf einer beliebigen Linie befindet, von der Größe ( n ) der Entscheidungsmatrix.

( tRow ), erhöht um das 10 ^6- fache vom Logarithmus der Größe der Lösungsmatrix im Bereich von n von 50 bis 10 ⁸ , verringert sich die reduzierte Zeit mit zunehmendem n . Wenn die reduzierte Zeit für n = 50 10,7146 × 10 ^–6 Sekunden beträgt , wird die entsprechende Zeit für n = 10 ^{8 um} das 21-fache reduziert und beträgt 0,5084 × 10 ^–6Sekunden. Ein solches Verhalten des Algorithmus erscheint auf den ersten Blick irrtümlich, da es keine objektiven Gründe gibt, warum der Algorithmus ihn für kleine Werte von n als langsamer als für große Werte ansieht. Es liegt jedoch kein Fehler vor, und dies ist eine objektive Eigenschaft dieses Algorithmus. Dies liegt an der Tatsache, dass dieser Algorithmus aus drei Algorithmen besteht, die mit unterschiedlichen Geschwindigkeiten arbeiten. Darüber hinaus ändert sich die Anzahl der von jedem dieser Algorithmen verarbeiteten Zeilen mit zunehmendem Wert von n. Aus diesem Grund nimmt die Zählzeit im anfänglichen Wertebereich n = (10, 20, 30, 40) zu, da alle Berechnungen in diesem kleinen Bereich nur auf der Grundlage des fünften Verfahrensblocks durchgeführt werden, der sehr effizient, jedoch nicht so schnell wie arbeitet erster Block von Prozeduren. Angesichts der Zeit, die erforderlich ist, um die Dame in einer Zeile zu positionieren,nimmt mit zunehmender Größe des Schachbretts ab, so kann die zeitliche Komplexität dieses Algorithmus als abnehmend - linear bezeichnet werden.

Die Häufigkeit, mit der Back Tracking (BT) verwendet wurde . In allen Fällen eines Computerexperiments haben wir die Anzahl der Fälle mithilfe des BT-Verfahrens bei der Lösung jedes Problems verfolgt. Es wurde eine kumulative Zusammenfassung aller Fälle der Verwendung von BT erstellt, unabhängig davon, auf welche Basisebene bei der Suche nach einer Lösung zurückgekehrt wurde. Dies gab uns die Möglichkeit, für jede Stichprobe den Anteil der Entscheidungen zu bestimmen, bei denen das BT-Verfahren noch nie angewendet wurde. Abbildung 9 zeigt


Abb.9. Der Anteil der Entscheidungen in der Stichprobe, bei denen das Verfahren zur Rückverfolgung noch nie verwendet wurde, in einem

Diagramm, das zeigt, wie sich der Anteil der Fälle der Lösung ändert, ohne das BT-Verfahren ( Zero Back Tracking ) mit zunehmendem n zu verwenden . Es ist zu erkennen, dass im Wertebereich n = (7, ..., 100000) die Anzahl der Lösungen, in denen das BT-Verfahren noch nie angewendet wurde, 35% überschreitet. Darüber hinaus übersteigt im Wertebereich n = (320, ..., 22500) die Anzahl solcher Fälle 50%. Die effektivsten Ergebnisse wurden für ein Schachbrett mit einer Größe von 5000 x 5000 erzielt , bei dem in einer Stichprobe von 10.000 Kompositionen in 61,92% der Fälle „deterministisch“ vorgegangen wurdeLösen eines nicht deterministischen Problems, weil In 61,92% der Fälle wurde das BT-Verfahren nie angewendet. In den übrigen Lösungen wurde in 21,87% der Fälle das BT-Verfahren einmal, in 9,07% der Fälle zweimal und in 3,77% der Fälle dreimal angewendet. Zusammen macht dies 96,63% der Fälle aus. Die Tatsache, dass nach dem Wert n = 5000 die Anzahl der Fälle, in denen das Konfigurationsproblem ohne Verwendung der BT-Prozedur gelöst wird, allmählich abnimmt, hängt mit dem ausgewählten Modell für die Auswahl der Grenzwerte von baseLevel2 und baseLevel3 zusammen . Sie können diese Parameter ändern und die Anzahl der Lösungen erhöhen, ohne das BT-Verfahren zu verwenden. Dies führt jedoch zu einer Verlängerung der Rechenzeit, da die Beteiligung des fünften Blocks an der Funktionsweise des Algorithmus zunimmt.

Das Histogramm der Verteilung der Zeiterfassung . In 10 ist für einen Wert von n = 1000 ein Histogramm der Verteilung der Entnahmezeit für eine Million Entscheidungen dargestellt. Die nicht ganz gewöhnliche Ansicht des Verteilungshistogramms (das höchstwahrscheinlich der Nachtsilhouette hoher Gebäude ähnelt) ist nicht mit einem Fehler bei der Auswahl der Länge oder Anzahl der Intervalle verbunden. Dies ist eine natürliche Eigenschaft dieses Algorithmus. Zu verstehen


Abb.10. Ein Histogramm der Zusammenstellungszeit von Kompositionen beliebiger Größe. ( n = 1000 ; Stichprobengröße = 1.000.000 )

Berücksichtigen Sie, warum das Histogramm eine solche Form hat, die Verteilung der Aufnahmezeit für Zusammensetzungen mit derselben Größe. Als Beispiel werden wir aus der ersten Stichprobe alle Kompositionen auswählen, deren Größe 800 beträgt. In einer Stichprobe von einer Million waren 998 solcher Kompositionen enthalten. Fig. 11 zeigt ein Histogramm der Verteilung der Zählzeit für diese Probe. Aus der Abbildung ist ersichtlich, dass die Verteilung aus sechs separaten Histogrammen mit abnehmender Größe besteht.


Abb.11. Ein Histogramm der Kompilierungszeit von Kompositionen gleicher Größe (k = 800). ( n = 1000 ; Stichprobengröße = 998 )

Der Grund, warum die Kompilierungszeit von 998 Kompositionen, in denen jeweils 800 Königinnen zufällig verteilt sind, in 6 Gruppen "gruppiert" wird, weil das Back-Tracking- Verfahren verwendet wird. Das erste Histogramm in der Abbildung mit der maximalen Stichprobengröße zeigt die Lösungen, bei denen das BT-Verfahren noch nie angewendet wurde. Dies ist eine Gruppe der schnellsten Lösungen. Das zweite Histogramm, das wesentlich kleiner ist als das erste, sind diejenigen Lösungen, bei denen das BT-Verfahren nur einmal verwendet wurde. Daher ist die Entscheidungszeit in dieser Gruppe etwas länger als in der ersten. Dementsprechend wurde in der dritten Gruppe die BT-Prozedur zweimal verwendet, in der vierten - dreimal usw., d.h. Entscheidungen, bei denen das BT-Verfahren wiederholt angewendet wurde, wurden über einen längeren Zeitraum durchgeführt. Solche Lösungen bilden den langen rechten Schwanz der gewünschten Verteilung.

Falsch Negative Lösungen . Teilen wir alle möglichen Kompositionen durch einen beliebigen Wert von nzu positiv und negativ, dann gibt es unter den positiven Kompositionen diejenigen, die dieser Algorithmus als negativ einstufen kann. Dies liegt an der Tatsache, dass der Algorithmus innerhalb der durch die Suchparameter festgelegten Grenzen nicht den richtigen Weg finden kann, um solche Kompositionen zu vervollständigen. Wie die experimentellen Ergebnisse (Tabelle 2) zeigen, überschreitet die Anzahl solcher Fälle nicht 0,0001 der Probengröße und der Wert dieses Fehlers nimmt mit zunehmendem n ab . Zusätzlich gab es für alle Werte von n> 800 keinen einzigen Fall einer falsch negativen Lösung. Selbst eine Erhöhung des Stichprobenumfangs auf eine Million für n = 1000 führte nicht zu False NegativeEntscheidungen. Das Ergebnis erlaubt es uns, die folgende Regel zur Lösung des Problems zu formulieren: „Jede zufällige Zusammensetzung von k Damen, die konsistent auf einem beliebigen Schachbrett der Größe nxn verteilt ist, kann vervollständigt werden, bis eine vollständige Lösung vorliegt , oder es wird entschieden, dass diese Zusammensetzung negativ ist und nicht abgeschlossen sein. Die Wahrscheinlichkeit, eine solche Entscheidung zu treffen, überschreitet 0,0001 nicht . Mit zunehmender Größe eines Schachbretts sinkt die Wahrscheinlichkeit, falsche Entscheidungen zu treffen. Die zeitliche Komplexität des Algorithmus ist linear. “

8. Schlussfolgerungen

Es wird ein Algorithmus vorgestellt, der es ermöglicht, in linearer Zeit das gesamte Mengenproblem zu lösen, bis eine vollständige Lösung einer zufälligen Zusammensetzung von k Königinnen vorliegt , die konsistent auf einem Schachbrett beliebiger Größe nxn verteilt ist . Darüber hinaus wird für jede Zusammensetzung von k Königinnen (1 ≤ k <n ) eine Lösung bereitgestellt, falls vorhanden, oder es wird eine Entscheidung getroffen, dass diese Zusammensetzung nicht vervollständigt werden kann. Die Wahrscheinlichkeit eines Fehlers bei einer solchen Entscheidung überschreitet nicht 0,0001 und dieser Wert nimmt mit zunehmender Größe eines Schachbretts ab.

2. Die Funktionsweise dieses Algorithmus basiert auf der Verwendung von zwei wichtigen Regeln:

a) In der letzten Phase der Problemlösung wird aus allen verbleibenden freien Positionen eine ausgewählt, für die die Anzahl der freien Positionen minimal ist ( minimale Risikoregel ). Dies minimiert die Risiken, die mit der Möglichkeit verbunden sind, die letzten offenen Positionen in einigen der verbleibenden Linien auszuschließen.

b) Von allen vakanten Positionen in der betreffenden Linie wird diejenige Position ausgewählt, die den freien Positionen in den verbleibenden freien Linien einen minimalen Schaden zufügt (Regel des minimalen Schadens ). Mit " minimaler Schaden " ist die Auswahl einer solchen Position in einer Zeile gemeint, die die geringste Menge an freien Positionen in allen verbleibenden freien Zeilen ausschließt.

3. Es wurde festgestellt, dass als Ergebnis der Operation dieses Algorithmus die durchschnittliche Zeit, die erforderlich ist, um die Königin auf eine Zeile zu setzen, mit einer Zunahme des Werts von n abnimmt. Die durchschnittliche Zeit, die erforderlich ist, um die Dame in einer Zeile zu platzieren, wenn n 10 ⁸ ist, ist 21-mal kürzer als die entsprechende Zeit für den Fall n = 50.

4. Es wurde festgestellt, dass im Wertebereich n = (7, ..., 100000) die Anzahl der Lösungen, in denen das Rückverfolgungsverfahren noch nie angewendet wurde, 35% übersteigt. Darüber hinaus übersteigt im Wertebereich n = (320, ..., 22500) die Anzahl solcher Fälle 50%, was die hohe Effizienz dieses Algorithmus anzeigt.

5. Ein Modell für die Organisation des Back Tracking- Verfahrens wird vorgeschlagen., basierend auf der Trennung der Reihenfolge der Entscheidungsschritte auf den Grundebenen. Ein Level bedeutet einen bestimmten Entscheidungsschritt mit einer bestimmten Anzahl von Königinnen, die korrekt platziert wurden . Zur Berechnung der Werte der zweiten und dritten Grundstufe in Abhängigkeit von n werden Regressionsformeln angegeben .

6. Die Ergebnisse einer vergleichenden Analyse von zwei Zufallsauswahlmethoden, die als randSet & randSet und rand & rand bezeichnet werden , werden vorgestellt . Der randSet & randSet-Algorithmus hat sich als schnell, aber unhöflich erwiesen . Daher ist seine Verwendung beim Erreichen der zweiten Grundstufe begrenzt. Danach wird der Rand & Rand- Algorithmus verwendet., die nicht so schnell durchgeführt wird, sondern Königinnen effektiver auf ein Schachbrett legt.

7. Es wird ein effektiver Algorithmus zur Überprüfung der Korrektheit der n-Queens-Problemlösung angegeben . Dieses Programm dient auch dazu, die Richtigkeit einer zufälligen Zusammensetzung beliebiger Größe zu überprüfen. Das Programm arbeitet schnell genug. Beispielsweise beträgt die zur Validierung einer aus 5 Millionen Positionen bestehenden Lösung erforderliche Zeit 0,85 Sekunden.

9. Kommentare

1. Wie zu Beginn des Artikels angegeben, wurden Studien im Bereich von n Werten von 7 bis 100 Millionen durchgeführt. Das Programm wurde jedoch in einem größeren Bereich von n Werten getestet , bis zu einer Milliarde. In letzterem Fall musste das Programm allerdings aufgrund der Größe der Arrays leicht angepasst werden. Wenn die Größe des RAM dies zulässt, ist es daher möglich, Berechnungen für große Werte von n durchzuführen.

2. Die Werte der Basisindikatoren sowie die Grenzwerte für die Anzahl der Wiederholungen auf verschiedenen Ebenen wurden optimiert, um das Problem im gesamten Forschungsbereich zu lösen. Sie können in einem kleineren Bereich geändert werden und verkürzen die Zählzeit. Es ist wichtig, den Anteil der falsch negativen Lösungen nicht zu erhöhen .

3. In diesem Artikel habe ich die Zeit zum Drücken der Eingabetaste als Zeitmaß verwendet, um zu bewerten, wie schnell der Algorithmus arbeitet. Wenn das Ergebnis unmittelbar nach dem Drücken der Taste angezeigt wird, scheint es auf der Ebene der Benutzerwahrnehmung, dass das Programm "sehr" schnell arbeitet. Egal wie schnell der Algorithmus arbeitet, das Ergebnis wird erst auf dem Bildschirm angezeigt, wenn der Schlüssel vollständig ist. Aus diesem Grund schien es mir, dass eine solche bedingte Zeitmessung als Schwellenwert dienen kann, um die Geschwindigkeit verschiedener Algorithmen nicht genau zu vergleichen.

4. Philosophisch ... Während der Studie wurde eine Vielzahl von Veröffentlichungen zur Lösung nicht deterministischer Probleme betrachtet. In den meisten Fällen handelte es sich dabei um Aufgaben, bei denen unter den Bedingungen vorgegebener Beschränkungen in einem großen Staatenraum eine Auswahl getroffen werden musste. Im Vergleich war es interessant zu wissen, wie weit man bei der Lösung solcher Probleme mit dem mathematischen Standardansatz kommen kann. Ich hatte den Eindruck, dass es unmöglich ist, solche Probleme nur auf der Grundlage von Definitionen, Behauptungen und Beweisen zu lösen. Es scheint mir, dass es zur Lösung solcher Probleme notwendig ist, die Methoden der algorithmischen Mathematik unter Verwendung von Computersimulationen anzuwenden. Um die Gültigkeit dieser Schlussfolgerung zu demonstrieren, habe ich als einfaches Beispiel ein Schachbrett vorbereitet, dessen Größe 10 ist⁹ x 10 ⁹ zwei Kompositionen gleicher Größe, bestehend aus 999.999.482 Königinnen. Sie werden wie am Anfang des Artikels beschrieben erstellt und als zwei Dateien im Format .mat angezeigt. Sie können unter diesem Link heruntergeladen werden (zwei Testdateien) . Dateien sind ziemlich "schwer", die Größe jeder von ihnen beträgt etwa 3,97 GB. In 999 997 976 Zeilen (in 99,9998% der Fälle) stimmen die Positionen der Königinnen in beiden Kompositionen überein, und nur in willkürlichen 1506 Zeilen unterscheiden sich die Positionen der Königinnen.

Um die Zusammensetzungsdaten zu einer vollständigen Lösung zu vervollständigen, müssen Sie die Damen korrekt in die verbleibenden 518 freien Zeilen einfügen. Die Anzahl der möglichen Möglichkeiten, 518 Königinnen in den verbleibenden freien Linien anzuordnen (wobei nur die Anzahl der Möglichkeiten berücksichtigt wird, eine freie Position in der ausgewählten Linie auszuwählen), beträgt ungefähr ^10.146. Der Unterschied zwischen diesen beiden Zusammensetzungen besteht nur darin, dass eine davon positiv ist und bis zu einer vollständigen Lösung vervollständigt werden kann, und die andere Zusammensetzung negativ ist - sie kann nicht bis zu einer vollständigen Lösung vervollständigt werden. Frage: „Ist es möglich, auf der Grundlage eines strengen mathematischen Ansatzes (dh ohne Ausführung algorithmischer Rechenoperationen) zu bestimmen, welche dieser beiden Kompositionen positiv ist?“ Wenn dies nicht zu lösen ist, können wir davon ausgehen, dass der Satz durch Widerspruch bewiesen ist.

Ich möchte darauf hinweisen, dass unabhängig von der Herangehensweise an die rein mathematische Lösung dieses Problems der Status 518 * 10 ^{9 ermittelt werden muss}Zellen in den verbleibenden freien Zeilen. Um dies zu tun, ist es notwendig, jede Position von zuvor eingerichteten Königinnen zu berücksichtigen, und es gibt fast eine Milliarde von ihnen, um die Beschränkungen festzulegen, die jede eingerichtete Königin den freien Positionen in den verbleibenden 518 Linien auferlegt. Ich habe keinen „Drehpunkt“ gefunden, der es mir erlaubt, diese Arbeit nur auf der Grundlage eines rein mathematischen Ansatzes ohne algorithmische Berechnungen durchzuführen.

Ich habe hier ein minimales Beispiel gegeben, das nur aus zwei Kompositionen besteht. Bei Bedarf kann die Anzahl solcher Zusammensetzungen erhöht werden.

Es ist anzumerken, dass auf der Grundlage des vorgeschlagenen linearen Algorithmus, der leicht an das Arbeiten mit großen Zusammensetzungen angepasst ist, die Aufgaben der beiden Testzusammensetzungen abgeschlossen werden können, bis eine vollständige Lösung auf Desktop-13 ausgeführt wird In ca. 4,5 Minuten (ohne Ladezeit der Eingabedaten).

10. Zugabe

Das Handeln von Professoren, die fähige Aufgaben empfehlen, die die Studenten entwickeln und erforschen können, verdient Respekt. Dies erfordert einen erheblichen Aufwand, aber bei der Überwindung von Schwierigkeiten sieht der Forscher andere komplexe Aufgabenstellungen anders. Ich dachte, es wäre nützlich, die Optionen zum Festlegen des n-Queens-Problems für solche Zwecke zu erweitern. Wenn Sie dieselbe Aufgabe aus verschiedenen Perspektiven betrachten, können Sie verschiedene Dinge sehen. Nachfolgend einige davon.

1. Betrachten Sie das Problem, n Damen auf einem rechteckigen „Schachbrett“ der Größe nxm anzuordnen . Bezeichne k = m - n . Es sei eine Lösung erhalten, und in jedem von nIn jeder Reihe befand sich eine Königin. Positionen, an denen sich Königinnen befinden, werden von der weiteren Betrachtung ausgeschlossen. Jetzt gibt es in jeder Zeile m-1 freie Position. In den verbleibenden freien Positionen finden wir wieder eine Lösung. Nach wie vor schließen wir die Positionen aus, an denen sich die Königinnen der zweiten Lösung befinden. Jetzt gibt es in jeder Reihe m-2 freie Positionen. Offensichtlich kreuzen sich die erste und die zweite Lösung in keiner Zeile - sie sind orthogonal. Es ist erforderlich, die maximale Anzahl von zueinander orthogonalen Lösungen für verschiedene Werte von k zu bestimmen . Wenn für den Wert k = 0 n zueinander orthogonale Lösungen gefunden werdendann wird der Royal Latin Square gebaut.

Bemerkung . Das Papier Grigoryan E. (2018) , die für jede Lösung gezeigt , n-Queens Problem gibt es eine ergänzende Lösung ist, die nicht mit ihrem interferiert. Dies bedeutet, dass für einen beliebigen Wert von n die Menge aller Lösungen des n-Queens-Problems in zwei gleich große Teilmengen aufgeteilt wird. Jede Lösung aus der zweiten Teilmenge ist eine Komplementärlösung zur entsprechenden Lösung aus der ersten Teilmenge. Die Regel ist ganz einfach: Wenn Q1 (i) eine Lösung aus der ersten Menge ist, dann ist die entsprechende komplementäre Lösung Q2 (i)aus der zweiten Teilmenge wird durch die Formel Q2 (i) = n + 1 - Q1 (i) bestimmt, wobei i = (1, ..., n) . Diese Regel erklärt die Tatsache, dass die Anzahl aller Lösungen des n-Queens-Problems für einen beliebigen Wert von n immer eine gerade Zahl ist. (Diese Regel erlaubt es uns, die Zeit für die Berechnung aller vollständigen Lösungen für eine beliebige Größe n des Schachbretts zu halbieren . Wenn wir die Gesamtzahl aller Lösungen mit 2 * k bezeichnen , dann ist der Wert k gleich dem Index in der sequentiellen Liste aller Lösungen, wenn Q (k) + Q ( k + 1) = n + 1 ).

2. In der anfänglichen Formulierung des Problems n-Qeens Problem , nachdem die Königin in Position (i, j) gebracht wurdewerden die folgenden Aktionen ausgeführt:

a) Alle Zellen der Zeile i und der Spalte j

werden ausgeschlossen, b) Alle Zellen, die sich auf der Linie der linken und rechten Diagonalen befinden, die durch die Zelle (i, j) verlaufen, werden ausgeschlossen .

Wir ändern die Bedingung b) in der Erklärung des Problems. Anstatt Zellen zu eliminieren, werden wir die Zellenvermittlung verwenden. Wenn die Zelle in der Linie der linken oder rechten Diagonale frei ist, schließen wir sie, wenn die Zelle geschlossen ist, öffnen wir sie. Dies erleichtert das Finden einer Lösung. Anstelle der quadratischen Matrix nxn betrachten wir jedoch eine rechteckige Matrix der Größe nx (n - k) . Für einen gegebenen Wert von n ist es erforderlich, den Maximalwert von k zu findenbei denen mindestens drei orthogonale Lösungen erhalten werden können. Wie ändert sich der Wert von k mit zunehmendem Wert von n ?

3. Ändern Sie einige Bedingungen in der Anfangsformulierung des Problems mit dem n-Queens-Problem . Wenn die Dame an Position (i, j) auf einem Schachbrett der Größe nxn positioniert ist :

a) schließen wir alle Zellen in Zeile i aus ,

b) wenn der Index j eine gerade Zahl ist, dann:

b1) schließen wir Zellen in geraden Zeilen der Spalte j aus,

b2) schließen wir Zellen in aus gerade Linien, die die linken und rechten Diagonalen schneiden und durch die Zelle (i, j) verlaufen ,

c) Wenn Index j , b1) b2) , .

3.1 (Sloane-2016) , nQueens Problem , n=(8, 9, 10, 11, 12, 13, 14, 15, 16) , (92, 352, 724, 2680, 14200, 73712, 365596, 2279184, 14772512) . , b) c)?

3.2 Grigoryan (2018) ist bekannt, dass, wenn wir die Häufigkeit der Beteiligung verschiedener Zellen der Lösungsmatrix an der Bildung einer Liste aller Lösungen bestimmen, harmonische Beziehungen zwischen allen Zellen in Form vertikaler und horizontaler Symmetrien der entsprechenden Frequenzen bestehen. Dies bedeutet, wenn wir annehmen, dass k <n / 2 ist , ist die Frequenz der Zellen der k-ten Zeile identisch mit der Frequenz der Zellen der Zeile n-k + 1 . In ähnlicher Weise ist die Frequenz der Zellen der k-ten Spalte identisch mit der Frequenz der Zellen der Spalte n-k + 1 . Frage: "Wie werden sich diese harmonischen Beziehungen im Kontext der Aufgabe verändern?"

4. Alle Zellen eines Schachbretts sind durch ihre Farbe in zwei Klassen unterteilt. Es wird angenommen, dass eine Farbe weiß und die andere schwarz ist. Betrachten Sie zwei Schachbretter und legen Sie eines so auf das andere, dass die Kanten vollständig zusammenfallen. Als Ergebnis erhalten wir ein "Sandwich" aus zwei Schachbrettern, in denen die Anordnung der weißen und schwarzen Zellen übereinstimmt. Die Aufgabe besteht darin, auf zwei Tafeln gleichzeitig Lösungen zu finden, wobei folgende Bedingungen zu beachten sind:

a) Befindet sich die Dame auf einem der Tafeln auf einem schwarzen Feld mit den Indizes (i, j) , dann:

- auf beiden Tafeln alle schwarzen Felder, die auftreten in Zeile I und Spalte J ,

- Auf beiden Brettern sind alle schwarzen Zellen ausgeschlossen, die sich entlang der linken und rechten Diagonalen befinden, die durch die Zelle (i, j) verlaufen .

b) Befindet sich die Dame auf einem der Bretter auf einem weißen Feld mit den Indizes (i, j) , werden alle Aktionen von Absatz a) nur für weiße Felder ausgeführt.

5. Stellen Sie sich vor, dass in einer Lösungsmatrix der Größe nxn Zeilen mit einem Schritt von k Zellen relativ zueinander nach rechts oder links verschoben werden können . Wenn darüber hinaus die vorherige Reihe beispielsweise nach links verschoben wurde, sollte die nächste Reihe nach rechts verschoben werden, d.h. Jede nächste Zeile wird in die entgegengesetzte Richtung zur vorherigen Zeile verschoben. Durch diese Konstruktion erhalten wir eine rechteckige Größenmatrixnx (n + k) , wobei in jeder Zeile k Zellen vom Zeilenanfang oder vom Zeilenende von der Betrachtung ausgeschlossen werden. Die Aufgabe besteht darin , den Maximalwert von k für einen beliebigen Wert von n zu finden, für den es mindestens eine Lösung für das n-Queens-Problem gibt . Stellen Sie sich eine Variante des Problems vor, bei der der Versatz einer Zeile in Bezug auf eine andere eine Zufallszahl ist, die von k1 bis k2 reicht . 6. Die eindimensionale Formulierung des nQueens-Problems . Auf der Halbachse seien n Segmente beliebiger Länge von 1 bis n angeordnet . Teilen Sie jedes Segment durch n


Zellen beliebiger Größe und innerhalb jedes Segments Zellen von 1 bis n . Wir nennen solche Zellen offen. Es erfordert eine enge eine Zelle auf jedes Segment, die folgenden Einschränkungen Berücksichtigung

a) Wir können eine offenzellige mit Index wählen j der i - ten Segment , wenn:

D1 (r) = 0;

D2 (t) = 0;

wobei r = n + j - i, t = j + i, D1 und D2 eindimensionale Steuerfelder sind, die aus 2n Zellen bestehen, die zuvor auf Null gesetzt wurden.

b) Nach dieser Auswahl werden Segment i und Zellen mit der Nummer j geschlossenin allen verbleibenden freien Segmenten. Es ist auch notwendig, die entsprechenden Zellen in den Kontrollfeldern zu schließen:

D1 (r) = 1;

D2 (t) = 1;

In dieser Einstellung ist die Aufgabe völlig identisch mit der ursprünglichen. Interessant ist die Formulierung dieses Problems mit anderen Randbedingungen. Wenn beispielsweise anstelle der Formeln:
r = n + j - i, t = j + i, ,
werden andere Verhältnisse berücksichtigt werden, die funktionell verknüpft sind Indizes r und t - Indizes (i, j) eine Matrix zu machen.

7. Der Wortlaut der Aufgabe anhand einer Urne mit Kugeln (identisch mit dem vorherigen Wortlaut). Angenommen, es gibt n Urnen mit den Nummern 1 bis nund in jeder Urne gibt es n Kugeln, die ebenfalls von 1 bis n nummeriert sind . Erfordert urn von jedem Ball entfernt, die folgenden Einschränkungen Berücksichtigung

a) Wir um den Ballon mit der Nummer auswählen können j der i th urn , wenn:

D1 (r) = 0 ,

D2 (t) = 0 ,

wobei r = n + j - i, t = j + i, D1 und D2 sind eindimensionale Steuerfelder, die aus 2n Zellen bestehen, die zuvor auf Null gesetzt wurden.

b) Nach dieser Auswahl werden die Wahlurne i und die Bälle mit der Nummer j in allen verbleibenden freien Wahlurnen geschlossen . Es ist auch notwendig, die entsprechenden Zellen in den Kontrollfeldern zu schließen:

D1 (r) = 1 ,

D2 (t) = 1 .

In dieser Einstellung ist die Aufgabe völlig identisch mit der ursprünglichen. Wie im vorherigen Fall ist die Erklärung dieses Problems mit anderen Bedingungen von Interesse, die die Indizes r und t funktional mit den Indizes (i, j) der Entscheidungsmatrix verbinden.

8. Das Spiel . Betrachten Sie ein Schachbrett der Größe nxn . Lassen Sie uns die Farbe zu den Königinnen zurückbringen, lassen Sie einige Königinnen weiße Farbe haben, andere schwarz. Wir geben auch die abwechselnde weiße und schwarze Farbe an die Zellen des Schachbretts zurück, basierend auf der Tatsache, dass die Zelle mit dem Index (1, n)sollte weiß sein. Alle Zellen zu Beginn des Spiels gelten als frei. Weiße Königinnen machen den ersten Schritt. Der Spieler platziert die Dame in eine beliebige freie Zelle mit Indizes (i, j) . Lass es eine weiße Zelle sein. Infolge dieser Auswahl werden sie geschlossen:

a) alle weißen Zellen der Zeile i ,

b) alle weißen Zellen der Spalte j ,

c) alle weißen Zellen, die auf der linken und rechten Diagonale liegen und durch die Zelle (i, j) verlaufen .

Wenn sich herausstellt, dass die Zelle (i, j) schwarz ist, sind alle Punkte (a, b, c) erfülltDementsprechend sind alle schwarzen Zellen geschlossen. Als nächstes führt Schwarz den Zug aus und platziert die Dame in eine der verbleibenden freien Zellen. Danach schließen sich die Zellen auf ähnliche Weise wie oben beschrieben. Der Zeitpunkt, an dem über den nächsten Schritt nachgedacht werden soll, ist festgelegt und wird von den Parteien vereinbart. Wenn einer der Spieler während der angegebenen Zeit seinen Zug nicht beendet, wird das Spiel auf den anderen übertragen. Das Spiel endet, wenn beide Spieler nacheinander nicht in der angegebenen Zeit an der Reihe sind. Derjenige, der mehr Königinnen auf dem Brett platzieren kann, gewinnt.

9. Auf die Stabilität der zufälligen Auswahl. Betrachten Sie das randSet & randSet-Modell . Als Ergebnis des Vergleichs von n zufälligen Paaren von Zeilen- und Spaltenindizes ist es in der ersten Stufe des Zyklus möglich, die Königinnen im Durchschnitt bei festzulegenk * n Zeilen. Der Wert von k kann als konstanter Wert von 0,6 betrachtet werden. Sein Wert variiert von 0,605701 bei n = 10 und bis 0,599777 bei n = 10 ⁶ , und mit zunehmendem n nimmt die Varianz dieses Wertes ab. Was ist der Grund für eine solche "Beständigkeit"? Warum ist es mit einer zufälligen Auswahl des Zeilenindex und des Positionsindex der Dame in dieser Zeile auf der Grundlage von zwei Listen von Zahlen, die auf der Grundlage einer zufälligen Permutation von Zahlen von 1 bis n erhalten wurden, möglich, die Damen (im Durchschnitt) auf 60% der Zeilen konsistent zu platzieren?

10. Die Größe des Schachbretts sei nxn . Basierend auf dem randSet & randSet-VerfahrenLege die Königinnen auf das Schachbrett, bis der Suchzweig eine Sackgasse erreicht. Bezeichnen Sie die Länge der so erhaltenen Zusammensetzung mit k . Wenn für einen gegebenen Wert von n diese Prozedur viele Male wiederholt wird und ein Histogramm der Verteilung der Werte von k erstellt wird , zeigt sich, dass sich die Änderung der Häufigkeit des Auftretens von Ereignissen von der Änderung der Häufigkeit des Auftretens von Ereignissen nach diesem Wert unterscheidet. Wenn das Histogramm auf der Grundlage des Modalwerts in zwei Teile unterteilt ist, stimmt der linke Teil nicht mit dem rechten Teil überein. Dieses Muster ist charakteristisch für jeden Wert von n. Warum nimmt die Häufigkeit des Eintretens von Ereignissen nach dem Übergang der Länge der Komposition über den Modalwert eine andere Form an? Unter einem Ereignis verstehen wir das Erhalten einer Komposition einer bestimmten Größe, bevor ein Zustand der Sackgasse erreicht wird.

Literatur

1. Nauck, F. (1850). Briefwechsel mit allen fur alle . Illustrierte Zeitung, 15, 182.

2. Gent, IP, Jefferson, C. & Nightingale, P. (2017). Komplexität der Fertigstellung von n-Queens ,
Journal of Artificial Intelligence Research., 59, 815-848.

3. Sosic, R. & Gu, J. (1990). Ein polynomieller Zeitalgorithmus für das n-Königinnen-Problem . SIGART Bulletin, 1 (3), 7–11.

4. Richards, M. (1997). Backtracking-Algorithmen in MCPL unter Verwendung von Bitmustern und Rekursion .
Tech. rep., Computerlabor, Universität Cambridge.

5. Randomisierungsmethoden im Algorithmusdesign , Proceedings of a DIMACS Workshop, Princeton, New Jersey, USA, December 12-14, 1997. DIMACS Series in Discrete Mathematics and Theoretical Computer Science 43, DIMACS/AMS 1999, ISBN 978-0-8218-0916-7

6. Grigoryan E. (2018). Investigation of the Regularities in the Formation of Solutions n-Queens Problem . Modeling of Artificial Intelligence, 5(1), 3-21

7. Sloane N.-JA (2016). The on-line encyclopedia of integer sequences.