Hallo allerseits! Die Neujahrsfeiertage sind zu Ende, sodass wir wieder bereit sind, nützliches Material mit Ihnen zu teilen. Eine Übersetzung dieses Artikels wurde in Erwartung des Starts eines neuen Streams für den Kurs "Algorithmen für Entwickler" erstellt .
Lass uns gehen!
Die Methode der Rückübertragung von Fehlern ist wahrscheinlich die grundlegendste Komponente eines neuronalen Netzwerks. Es wurde zum ersten Mal in den 1960er Jahren beschrieben und fast 30 Jahre später von Rumelhart, Hinton und Williams in einem Artikel mit dem Titel
„Repräsentationen durch Fehler in der Rückübertragung
lernen“ populär gemacht.
Das Verfahren wird verwendet, um ein neuronales Netzwerk unter Verwendung der sogenannten Kettenregel (der Differenzierungsregel einer komplexen Funktion) effektiv zu trainieren. Einfach ausgedrückt, nach jedem Durchlauf durch das Netzwerk führt die Rückwärtsausbreitung einen Durchlauf in die entgegengesetzte Richtung durch und passt die Modellparameter (Gewichte und Verschiebungen) an.
In diesem Artikel möchte ich den Prozess des Lernens und Optimierens eines einfachen neuronalen 4-Schicht-Netzwerks aus mathematischer Sicht detailliert betrachten. Ich glaube, dass dies dem Leser helfen wird, die Funktionsweise von Backpropagation zu verstehen und ihre Bedeutung zu erkennen.
Definieren eines neuronalen Netzwerkmodells
Das vierschichtige neuronale Netzwerk besteht aus vier Neuronen in der Eingangsschicht, vier Neuronen in den versteckten Schichten und einem Neuron in der Ausgangsschicht.
Ein einfaches Bild eines vierschichtigen neuronalen Netzwerks.Eingabeebene
In der Abbildung stellen violette Neuronen die Eingabe dar. Dies können einfache skalare Größen oder komplexere Vektoren oder mehrdimensionale Matrizen sein.
Gleichung, die die Eingänge xi beschreibt.Der erste Aktivierungssatz (a) entspricht den Eingabewerten. "Aktivierung" ist der Wert eines Neurons nach Anwendung der Aktivierungsfunktion. Siehe unten für weitere Details.
Versteckte Schichten
Die Endwerte in verborgenen Neuronen (in der grünen Abbildung) werden unter Verwendung von zl-gewichteten Eingaben in Schicht I und einer
I- Aktivierung in Schicht L berechnet. Für die Schichten 2 und 3 lauten die Gleichungen wie folgt:
Für l = 2:
Für l = 3:
W
2 und W
3 sind die Gewichte auf den Schichten 2 und 3 und b
2 und b
3 sind die Offsets auf diesen Schichten.
Die Aktivierungen a
2 und a
3 werden mit der Aktivierungsfunktion f berechnet. Zum Beispiel ist diese Funktion f nicht linear (wie
Sigmoid ,
ReLU und
hyperbolischer Tangens ) und ermöglicht es dem Netzwerk, komplexe Muster in den Daten zu untersuchen. Wir werden nicht näher darauf eingehen, wie Aktivierungsfunktionen funktionieren, aber wenn Sie interessiert sind, empfehle ich Ihnen dringend, diesen wunderbaren
Artikel zu lesen.
Wenn Sie genau hinsehen, werden Sie feststellen, dass alle x, z
2 , a
2 , z
3 , a
3 , W
1 , W
2 , b
1 und b
2 keine in der Figur eines neuronalen Netzwerks mit vier Schichten gezeigten Indizes haben. Tatsache ist, dass wir alle Parameterwerte in Matrizen zusammengefasst haben, die nach Ebenen gruppiert sind. Dies ist eine Standardmethode für die Arbeit mit neuronalen Netzen und sehr komfortabel. Ich werde jedoch die Gleichungen durchgehen, damit es keine Verwirrung gibt.
Nehmen wir als Beispiel Schicht 2 und ihre Parameter. Dieselben Operationen können auf jede Schicht des neuronalen Netzwerks angewendet werden.
W
1 ist die Matrix der Gewichte der Dimension
(n, m) , wobei
n die Anzahl der Ausgangsneuronen (Neuronen in der nächsten Schicht) und
m die Anzahl der Eingangsneuronen (Neuronen in der vorherigen Schicht) ist. In unserem Fall ist
n = 2 und
m = 4 .
Hier entspricht die erste Zahl im Index einer der Gewichte dem Neuronenindex in der nächsten Schicht (in unserem Fall ist dies die zweite verborgene Schicht), und die zweite Zahl entspricht dem Neuronenindex in der vorherigen Schicht (in unserem Fall ist dies die Eingabeschicht).
x ist der Eingangsvektor der Dimension (
m , 1), wobei
m die Anzahl der Eingangsneuronen ist. In unserem Fall ist
m = 4.
b
1 ist der Verschiebungsvektor der Dimension (
n , 1), wobei
n die Anzahl der Neuronen in der aktuellen Schicht ist. In unserem Fall ist
n = 2.
Nach der Gleichung für z
2 können wir die obigen Definitionen von W
1 , x und b
1 verwenden , um die Gleichung z
2 zu erhalten :
Schauen Sie sich nun die Abbildung des obigen neuronalen Netzwerks genau an:
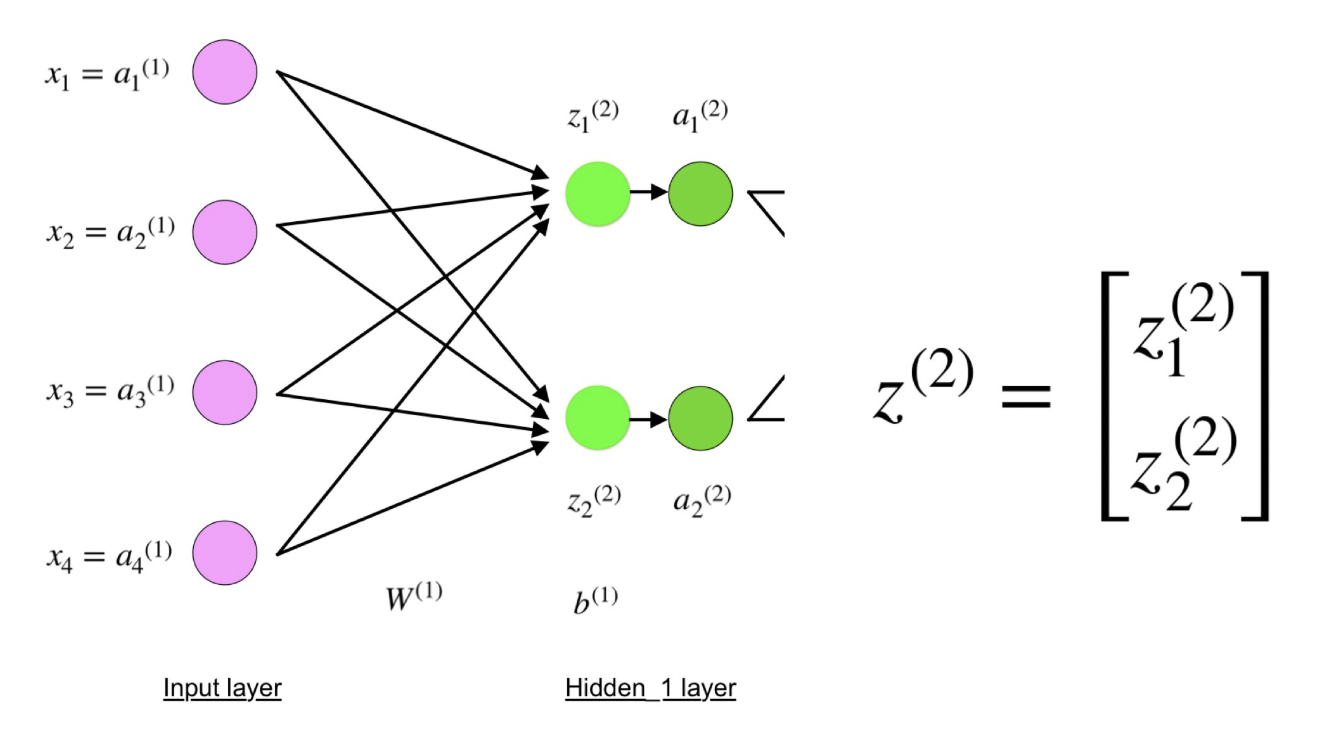
Wie Sie sehen können, kann z
2 als z
1 2 und z
2 2 ausgedrückt werden, wobei z
1 2 und z
2 2 die Summen der Produkte jedes Eingabewerts x
i durch das entsprechende Gewicht W
ij 1 sind .
Dies führt zu der gleichen Gleichung für z
2 und beweist, dass die Matrixdarstellungen z
2 , a
2 , z
3 und a
3 wahr sind.
Ausgabeschicht
Der letzte Teil des neuronalen Netzwerks ist die Ausgabeschicht, die den vorhergesagten Wert angibt. In unserem einfachen Beispiel wird es in Form eines einzelnen blau gefärbten Neurons dargestellt und wie folgt berechnet:
Wieder verwenden wir die Matrixdarstellung, um die Gleichung zu vereinfachen. Sie können die obigen Methoden verwenden, um die zugrunde liegende Logik zu verstehen.
Direktvertrieb und Auswertung
Die obigen Gleichungen bilden eine direkte Verteilung durch das neuronale Netz. Hier ist eine kurze Übersicht:
(1) - Eingabeschicht
(2) - der Wert des Neurons in der ersten verborgenen Schicht
(3) - Aktivierungswert auf der ersten verborgenen Ebene
(4) - der Wert des Neurons in der zweiten verborgenen Schicht
(5) - Aktivierungswert auf der zweiten verborgenen Ebene
(6) - AusgangsschichtDer letzte Schritt im direkten Durchlauf besteht darin, den vorhergesagten Ausgabewert
s relativ zum erwarteten Ausgabewert
y auszuwerten.
Die Ausgabe y ist Teil des Trainingsdatensatzes (x, y), wobei
x die Eingabe ist (wie wir uns aus dem vorherigen Abschnitt erinnern).
Die Schätzung zwischen
s und
y erfolgt über die Verlustfunktion. Es kann einfach als
Standardfehler oder komplexer als
Kreuzentropie sein .
Wir nennen diese Verlustfunktion C und bezeichnen sie wie folgt:
Wo die
Kosten gleich dem Standardfehler, der Querentropie oder einer anderen Verlustfunktion sein können.
Basierend auf dem Wert von C „weiß“ das Modell, wie sehr seine Parameter angepasst werden müssen, um sich dem erwarteten Ausgabewert von
y anzunähern . Dies geschieht mit der Backpropagation-Methode.
Rückausbreitung von Fehlern und Berechnung von Gradienten
Basierend auf einem Artikel von 1989 wurde die Backpropagation-Methode:
Passt die Gewichtung der Verbindungen im Netzwerk ständig an, um die Differenz zwischen dem tatsächlichen Ausgangsvektor des Netzwerks und dem gewünschten Ausgangsvektor zu minimieren .
und
... ermöglicht es, nützliche neue Funktionen zu erstellen, die die Rückübertragung von früheren und einfacheren Methoden unterscheiden ...Mit anderen Worten, Backpropagation zielt darauf ab, die Verlustfunktion durch Anpassen der Gewichte und Offsets des Netzwerks zu minimieren. Der Grad der Anpassung wird durch die Gradienten der Verlustfunktion in Bezug auf diese Parameter bestimmt.
Eine Frage stellt sich:
Warum Steigungen berechnen ?
Um diese Frage zu beantworten, müssen wir zunächst einige Computerkonzepte überarbeiten:
Der Gradient der Funktion C (x
1 , x
2 , ..., x
m ) bei x ist der
Vektor der partiellen Ableitungen von C in
Bezug auf
x .
Die Ableitung der Funktion C spiegelt die Empfindlichkeit gegenüber einer Änderung des Wertes der Funktion (Ausgabewert) im Verhältnis zu der Änderung ihres Arguments
x (
Eingabewert ) wider. Mit anderen Worten, die Ableitung sagt uns, in welche Richtung sich C. bewegt.
Der Gradient zeigt an, wie stark der Parameter
x (in positiver oder negativer Richtung) geändert werden muss, um C zu minimieren.
Diese Gradienten werden mit einer Methode berechnet, die als Kettenregel bezeichnet wird.
Für ein Gewicht (w
jk )
l ist der Gradient:
(1) Kettenregel
(2) Definitionsgemäß ist m die Anzahl der Neuronen pro 1-Schicht
(3) Ableitungsberechnung
(4) Endwert
Ein ähnlicher Satz von Gleichungen kann auf (b j ) l angewendet werden :
(1) Kettenregel
(2) Ableitungsberechnung
(3) EndwertDer gemeinsame Teil in beiden Gleichungen wird oft als "lokaler Gradient" bezeichnet und wie folgt ausgedrückt:
Ein "lokaler Gradient" kann leicht mit einer Kettenregel bestimmt werden. Ich werde diesen Prozess jetzt nicht malen.
Mit Farbverläufen können Modellparameter optimiert werden:
Bis das Stoppkriterium erreicht ist, wird Folgendes ausgeführt:
Algorithmus zur Optimierung von Gewichten und Offsets (auch Gradientenabstieg genannt)
- Die Anfangswerte von w und b werden zufällig ausgewählt.
- Epsilon (e) ist die Lerngeschwindigkeit. Es bestimmt die Wirkung des Verlaufs.
- w und b sind Matrixdarstellungen von Gewichten und Offsets.
- Die Ableitung von C in Bezug auf w oder b kann unter Verwendung von partiellen Ableitungen von C in Bezug auf einzelne Gewichte oder Offsets berechnet werden.
- Die Abbruchbedingung ist erfüllt, sobald die Verlustfunktion minimiert ist.
Ich möchte den letzten Teil dieses Abschnitts einem einfachen Beispiel widmen, in dem wir den Gradienten C für ein Gewicht (w
22 )
2 berechnen.
Vergrößern wir den unteren Rand des oben genannten neuronalen Netzwerks:
Visuelle Darstellung der Backpropagation in einem neuronalen NetzwerkDas Gewicht (w
22 )
2 verbindet (a
2 )
2 und (z
2 )
2 , daher erfordert die Berechnung des Gradienten die Anwendung der Kettenregel auf (z
2 )
3 und (a
2 )
3 :
Die Berechnung des Endwertes der Ableitung von C aus (a
2 )
3 erfordert Kenntnis der Funktion C. Da C von (a
2 )
3 abhängt, sollte die Berechnung der Ableitung einfach sein.
Ich hoffe, dieses Beispiel hat es geschafft, etwas Licht in die Mathematik für die Berechnung von Verläufen zu bringen. Wenn Sie mehr wissen möchten, empfehle ich Ihnen dringend, die Artikelreihe Stanford NLP zu lesen, in der Richard Socher 4 großartige Erklärungen für die Backpropagation liefert.
Schlussbemerkung
In diesem Artikel habe ich ausführlich erklärt, wie die Rückübertragung eines Fehlers unter der Haube mit mathematischen Methoden wie der Berechnung von Gradienten, Kettenregeln usw. funktioniert. Wenn Sie die Mechanismen dieses Algorithmus kennen, werden Sie Ihre Kenntnisse über neuronale Netze vertiefen und sich bei der Arbeit mit komplexeren Modellen wohlfühlen. Viel Glück auf deiner tiefen Lernreise!
Das ist alles. Wir laden alle zu einem kostenlosen Webinar zum Thema "Baum der Segmente: einfach und schnell" ein.