Sonne, Wind und Wasser ver 0.2

Staffel Zwei

Physik des Segelns oder Segelns für Physiker

Während des Trainings in der Steuermannsschule erzählten uns erfahrene Praktiker, wie echte Segler den „rosa“ Wind sehen, den richtigen Winkel an einem Ort spüren und von räumlichem Kretinismus völlig unberührt bleiben. Offensichtlich verhindert die Ausbildung auf dem Gebiet der Physik, dass eine Person "rosa" Winde sieht, und macht einen Ort weniger empfindlich. Ich werde versuchen herauszufinden, wie sich die Yacht in Zahlen bewegt.

Was brauchen Sie, um eine Yacht zu digitalisieren?

1. Abschleppcharakteristik
   
2. Stabilitätsdiagramm
   
3. Segelgeometrie - live messen
   die Höhe des oberen Winkels der Grotte $$$h_ {gr top} = 11,2 Mio.$ ;
   Höhe des Heftwinkels der Grotte $$$h_ {gr hls} = 1,985 m$ ;
   Schlaufenwinkel $$$h_ {gr pc} = 2,179 m$ ;
   Abstand des Scheitelwinkels des Großsegels vom Mast $$$l_ {gr pc} = 2,96 m$ ;
   Höhe des oberen Stagsegelwinkels $$$h_ {st top} = 10 m$ ;
   Stapelhefthöhe $$$h_ {st sls} = 1.111 m$ ;
   Schlaufenwinkel $$$h_ {cst} = 1,5 m$ ;
   Grottenbereich $$$S_ {gr} = 17,2 m ^ 2$ ;
   Stagsegelbereich $$$S_ {st} = 14 m ^ 2$ ;
   Rumpf seitlicher Segelbereich $$$S_ {anf} = 7.315 m ^ 2$ ;
   Bereich der Frontalwindung des Rumpfes $$$S_ {fr} = 3 m ^ 2$ ;
   seitliche Projektion des Bereichs des Unterwasserkörpers $$$S_ {dn} w = 1,82 m ^ 2$ ;
   Bereich der Kiele und Skegs $$$S_ {ks} = 2,33 m ^ 2$ ;
   minimal möglicher Stagsegelwinkel $$$\ psi_ {ct} = 18 ^ o$ .
   
   Vielleicht war es für mich so unglücklich, aber keiner der Hersteller stimmte während meiner Suche nach der Yacht zu (konnte), diese Daten für ihre Yacht bereitzustellen. Ich bin mir sicher, dass der Designer der Yacht all diese Informationen hat, aber aus irgendeinem Grund kann ich sie nicht bekommen. Ich werde es selbst abbauen.
   Die Abschleppcharakteristik habe ich bereits durch die Digitalisierung der Yacht im Freeship-Programm erhalten : Als Belohnung für die Beharrlichkeit gibt das Programm sofort ein Stabilitätsdiagramm und einen Schwerpunkt sowie einen Seitenwiderstandsmittelpunkt und viele andere nützliche geometrische Informationen aus. Das Stabilitätsdiagramm zeigt, wie viel Drehmoment Sie auf die Yacht aufbringen müssen, um sie in einem bestimmten Winkel aufzustellen.
   
   
   
   

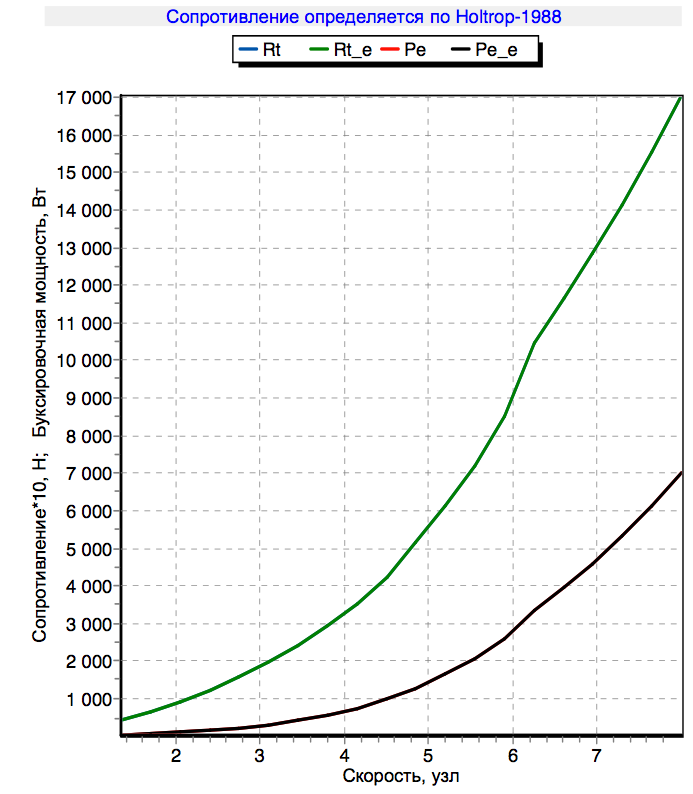
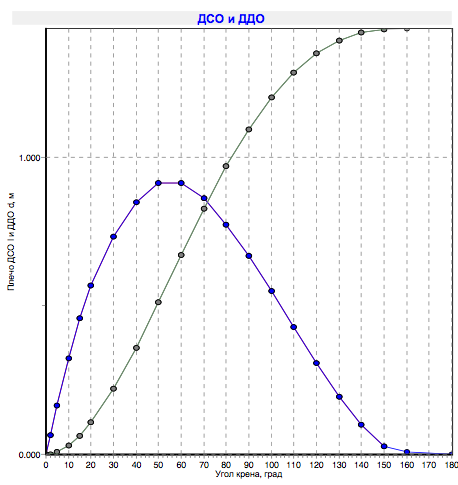
   Alle notwendigen Argumente werden gesammelt, fahren wir mit den Berechnungen fort.

   
   Offensichtlich überwindet die Yacht beim Vorwärtsfahren die Widerstandskraft des Gegenwinds. Die Gegenwindgeschwindigkeit entspricht der Geschwindigkeit der Yacht, ist jedoch in die entgegengesetzte Richtung gerichtet. Diese Analogie habe ich bereits bei der Auswahl eines Motors angewendet.
   

   $$

   $$R_ {fw} = 0,61 * S_ {fr} * v ^ 2, H,$$
   
   Dabei ist v die Geschwindigkeit des Schiffes.
   
   Gleichzeitig wirkt die Kraft des echten Windes auf die Yacht $$$F_ {rw}$ in einem bestimmten Winkel weht $$$\ alpha_ {rw}$ . Beide Winde erzeugen eine Kraft, die der Vektorsumme der Teilkräfte entspricht. Die sogenannte Kraft des Wimpelwinds - der Wind, der an Bord des Schiffes weht.
   
   Das Hauptproblem ist die Relativitätstheorie. Der Beobachter (und alle Messinstrumente) ist an Bord der Yacht und für ihn gibt es keine Möglichkeit, die Stärke und Richtung des echten Windes zu messen, aber er kann die Richtung messen - $$$\ alpha_ {vw}$ und Wimpelwindgeschwindigkeit - $$$v_ {vw}$ sowie die Richtung - $$$\ alpha$ gemessen an Bordkompass und Schiffsgeschwindigkeit - $$$v$ gemessen mit einem Onboard Lag (Tachometer).
   
   Die wahren Windparameter ermittle ich anhand von Messungen an Bordinstrumenten.
   $$$v_ {rw} = \ sqrt {v ^ 2 + v_ {vw} ^ 2-2 * v * v_ {vw} * cos (\ alpha_ {vw})}$ - echte Windgeschwindigkeit;
   $$$\ alpha_ {rw} = \ pi-arccos (\ frac {v_ {rw} ^ 2 + v ^ 2-v_ {vw} ^ 2} {2 * v * v_ {rw}})$ - der Winkel des echten Windes, der aus der Richtung "vorwärts" verschoben wurde.
   
   
   
   Für kleine Pokatushek macht das alles keinen Sinn. Die Verbindung zwischen dem echten Wind und dem Wimpelwind ist notwendig, um ausreichend lange Reisen zu planen (wenn sich das Ziel nicht in direkter Sichtlinie befindet). Schließlich wird auf einer Karte des Planeten mit der Angabe der tatsächlichen Winde (gemäß Wettervorhersagen) geplant, und die Bewegung der Yacht kommt von einem Wimpelwind.
   
   Nachdem die Verbindung zur Realität hergestellt wurde, ist es Zeit herauszufinden, wie die treibende Kraft entsteht. Es ist klar, dass der Wind die Segel füllt und das Boot über die Wellen fährt.
   
   Tatsächlich arbeitet ein Segel auf einer Yacht in zwei Hauptmodi:
   
   
   1. aerodynamischer Flügelmodus - bei Gegenwind,
      
   2. Aerodynamischer Bremsmodus - bei schönem Wind.
      
   
   Das Segelprofil ist so eingenäht, dass es bei Gegenwind die Form eines Flügels hat. Das heißt, es gibt einen Flügel, der sich mit einer bestimmten Geschwindigkeit relativ zur Luft bewegt - daher entsteht darin eine Hebekraft $$$F_ {air}$ . In Analogie zum Flügel eines Flugzeugs werde ich versuchen, seine Größe und Richtung relativ zur Yacht zu vereinfachen.
   
   Damit das Segel seine Arbeitsform annehmen kann, muss es relativ zur Windrichtung ein wenig gedreht werden. Der Drehwinkel wird "Anstellwinkel" genannt $$$\ alpha_ {a}$ . Zur Vereinfachung der Berechnungen wird der Flügel mit einer ebenen Platte verglichen, und die Unterschiede werden in Form einer Tabelle mit aerodynamischen Koeffizienten dargestellt , wobei Su der Auftriebsdifferenzkoeffizient und Cx der Widerstandsdifferenzkoeffizient ist. Die Hubkraft ist senkrecht zur Platte gerichtet und die Widerstandskraft ist parallel. Die Geometrie der Platte wird durch den aerodynamischen Dehnungskoeffizienten bestimmt $$$A_ {y} = h ^ 2 / S$ wo h ist die Höhe des Segels; S ist die Fläche des Segels.
   
   

   aber	Cy; Ay = 6	Cx	Cy; Ay = 3	Cx
   0	0	0,09	0	0,09
   5	0,83	0,1	0,65	0,1
   10	1.19	0,15	0.9	0,15
   15	1.22	0,3	1,1	0,25
   20	1.14	0,4	1.18	0,4
   25	1,06	0,485	1,2	0,5
   30	0,98	0,57	1	0,55
   40	0.9	0,73	0,82	0,65
   45	0,75	0,88	0,7	0,85
   50	0,6	1	0,6	1
   70	0,2	1.15	0,2	1.15
   90	0	1,2	0	1,2

   
   Der Flügel ist im Gegensatz zur Platte eine dreidimensionale Struktur, daher zeigt eine separate Tabelle, wie sich die Größe der Ausbuchtung des "Bauches" auf die Differenzkoeffizienten zur Platte auswirkt.
   

   Bauch	Su3	Cx3
   0,0667	-0,2	0,1
   0,1	0	0
   0,2	0	0,1
   0,25	0,1	0,2

   
   Segelkraftprojektion $$$F_ {air}$ zur Längsrichtung der Yacht - Nutzleistung:
   $$$F_ {s} = 0,61 * v_ {vw} ^ 2 * S * ((Cy + Cy3) * sin (\ alpha_ {vw}) - (Cx + Cx3) * cos (\ alpha_ {vw}))$ .
   Segelkraftprojektion $$$F_ {air}$ auf der Querrichtung der Yacht - Driftkraft:
   $$$F_ {d} = 0,61 * v_ {vw} ^ 2 * S * ((Cy + Cy3) * cos (\ alpha_ {vw}) - (Cx + Cx3) * sin (\ alpha_ {vw}))$ .
   
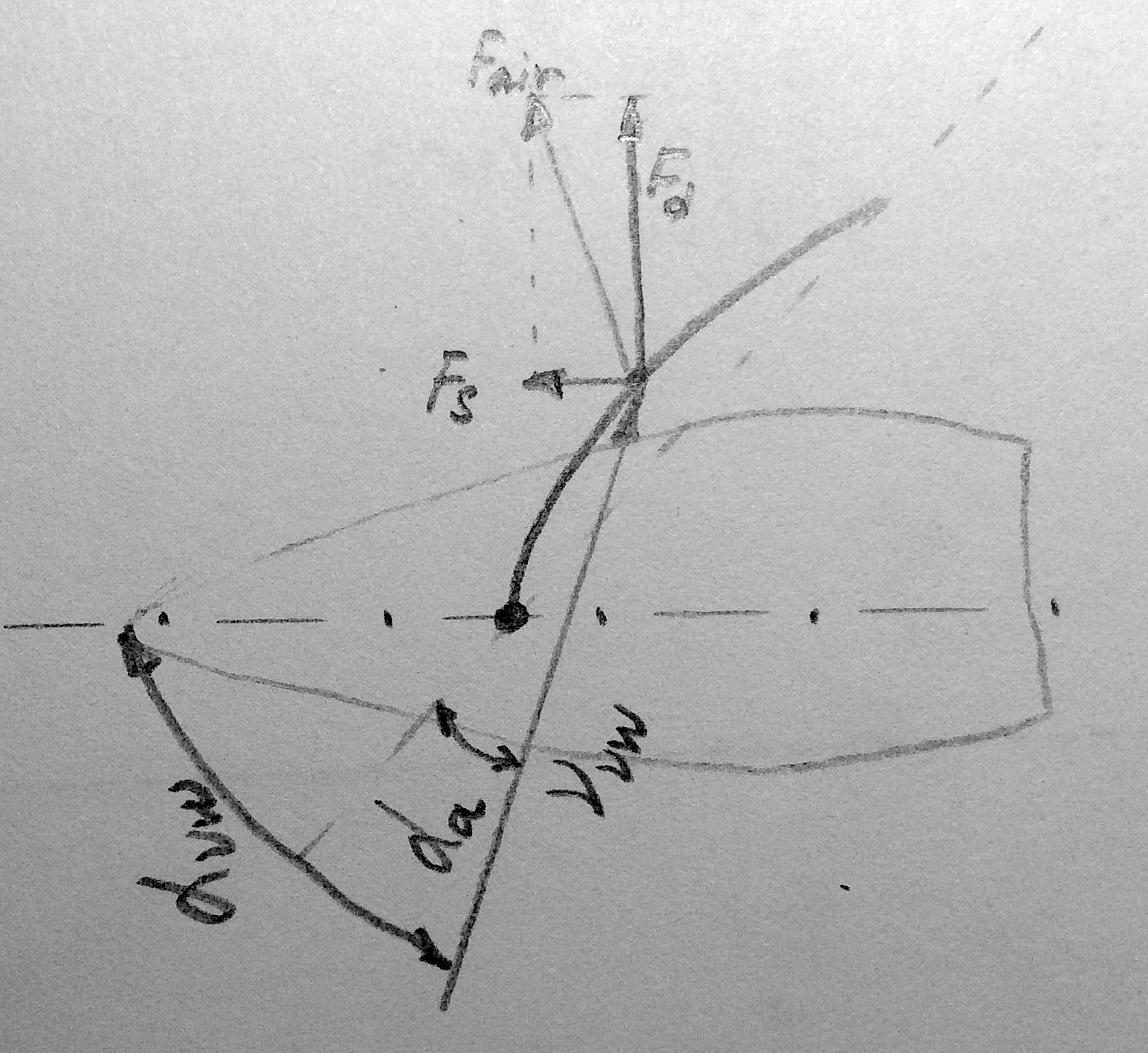
   Die Kraft des Windwiderstands des Rumpfes verlangsamt die Bewegung:
   $$$R_ {fw} = 0,61 * S_ {fr} * v_ {vw} ^ 2 * sin (\ alpha_ {vw})$
   Nachdem ich die Projektion der Kräfte erhalten habe, kann ich die Längs- und Quergeschwindigkeitsvektoren der Yacht finden. Längskomponente der Geschwindigkeit $$$v_ {dp}$ Ich finde die Abschleppcharakteristik laut Zeitplan.
   Bei der Querkomponente ist alles komplizierter.
   Zuerst müssen Sie die Höhe des Segelmittelpunkts ermitteln. Ein Segel ist ein Dreieck, bei dem eine Seite ein konvexer Bogen ist. Ich werde es als zwei Segel präsentieren: ein dreieckiges und ein sichelförmiges Stück. Die Fläche des Dreiecks wird als das halbe Produkt von Breite und Höhe berechnet, und die Fläche der "Sichel" ist die Differenz zwischen der Fläche des Segels und der Fläche des Dreiecks.
   

   $$

   $$S = (h_ {gr top} -h_ {gr hls}) * l_ {gr sht} / 2,$$
   wo $$$S_ {Sichel} = S_ {Gr} -S$
   Segelmittelhöhe:
   

   $$

   $$h_ {gr cp} = \ frac {h_ {gr \ Delta cp} * S \ Delta + ((h_ {gr oben} -h_ {gr pc}) * S_ {sichel} / 1,8)} {S_ {gr }},$$
   wo $$$h_ {gr \ Delta cp} = h_ {gr pc} + (h_ {gr top} + h_ {gr hl} -2 * h_ {gr pc}) / 3,$ Die Höhe des Segelmittelpunktes Segel Dreieck ohne Sichel.
   Normalerweise hat eine Yacht zwei Segel: das Hauptsegel und das vordere das Stagsegel. Das Stagsegel wird normalerweise ohne Sichel und dann in der Höhe der Segelmitte ausgeführt:
   

   $$

   $$h_ {st \ Delta cp} = h_ {st st} + (h_ {st top} + h_ {st hls} -2 * h_ {st sht}) / 3$$
   
   Segelzentrum gesamt:
   

   $$

   $$h _ {\ Sigma cpu} = \ frac {h_ {gr cp} * S_ {gr} + h_ {ct \ Delta cp} * S_ {ct}} {S_ {gr} + S_ {ct}}$$
   
   Jetzt kann ich den auf die Yacht einwirkenden Fersenmoment bestimmen:
   

   $$

   $$M_ {kr} = F_ {d} * h _ {\ Sigma cp}.$$
   
   Aus dem Stabilitätsdiagramm ermittle ich den Winkel der Yacht $$$\ phi$ .
   Ich drücke die Stärke des Treibens der Yacht aus:
   

   $$

   $$R_ {d} = 9,8 * 102 * (S_ {ks} * atan (\ frac {v_ {d}} {v_ {dp}}) * v_ {dp} ^ 2 * (cos (\ phi- \ gamma) -cos (& PHgr; + & ggr;) * 0,96+ (S_ {ks} + S_ {dp w}) * 1,15 * v_ {d} ^ 2 * cos (& PHgr;)),$$
   Wo ist der Winkel der Kiele der Zweikielyacht relativ zur Vertikalen?
   Die Kraft des Winddrucks auf den Körper gibt eine zusätzliche Drift.
   

   $$

   $$F_ {anf} = 0,61 * v_ {d} ^ 2 * S_ {anf} * cos (\ alpha_ {vw}).$$
   
   Geschwindigkeit $$$v_ {d}$ ist eine Halbteilungssubstitution bis zum Kräfteausgleich $$$F_ {d} + F_ {anf} = R_ {d}$ .
   Jetzt ist es offensichtlich, dass sich die Yacht "schräg" bewegt, d. H. hat Quer- und Längsbewegungsgeschwindigkeit. Dies bringt eine weitere Überraschung. Richtung - $$$\ alpha$ gemessen an Bordkompass und Schiffsgeschwindigkeit - $$$v = v_ {dp}$ Gemessen mit dem Onboard Lag (Tachometer) wird nur die Längskomponente angezeigt.
   Es ist notwendig, der Realität Dimensionen beizufügen. Der wahre Winkel des Schiffes $$$\ alpha_ {real}$ der "Spurwinkel" genannt:
   

   $$

   $$\ alpha_ {real} = atan (\ frac {v_ {d}} {v_ {dp}}) + \ alpha$$
   
   und kann von den gemessenen um 10-20 Grad abweichen.
   Die tatsächliche Geschwindigkeit der Yacht kann durch den Satz des Pythagoras bestimmt werden:
   

   $$

   $$v_ {real} = \ sqrt {v_ {dp} ^ 2 + v_ {d} ^ 2}.$$
   
   
   Abschließend werde ich anhand eines Berechnungsbeispiels für mein Boot die interessanteste Situation nennen - die Bewegung gegen den Wind. Es ist klar, dass Sie unter den Segeln nicht strikt gegen den Wind fahren, sondern in einem spitzen Winkel.
   
   Sie müssen vom vorderen Segel aus starten - das Stagsegel ist oben am Mast angebracht, der vordere Winkel zum Bug der Yacht und der hintere mit einem Blatt (weiches Kabel) durch die Rolle zur Winde. Seine Spannung reguliert den Winkel des Segels relativ zur Yacht. Minimaler Montagewinkel $$$\ psi_ {st min} = 18 ^ o$ bei maximaler Bogenspannung erhalten. Aerodynamische Verlängerung des Stagsegels $$$A_ {y st} = h_ {st} ^ 2 / S_ {st} = $ 5,$ . Mit der linearen Interpolationsmethode finde ich den optimalen Anstellwinkel $$$\ alpha_ {a} = 10 ^ o$ aus der Aerodynamikkoeffiziententabelle. Optimalitätskriterium - Maximierung $$$F_ {s st}$ worin Su = 1,17; Cx = 0,15. Das auf diese Weise installierte Stagsegel funktioniert effektiv in Richtung des Wimpelwinds $$$\ alpha_ {vw} = \ psi_ {ct} + \ alpha_ {a} = 18 + 10 = 28 ^ o$ . Gutes Wetter zum Segeln, wenn die Windgeschwindigkeit etwa 5-7 m / s beträgt. Für die Schönheit der Zahlen nehme ich $$$v_ {vw} = 6,55 m / s$ .
   
   Die Projektion der Stagsegelkraft auf die Längsrichtung der Yacht ist eine nützliche Kraft:
   

   $$

   $$F_ {s st} = 0,61 * 6,55 ^ 2 * 14 * ((1,17 + 0) * sin (28 * \ pi / 180) - (0,15 + 0) * cos (28 * \ pi / 180)) = 153,5 H$$
   
   Die Projektion der Stagsegelkraft auf die Querrichtung der Yacht - die Driftkraft:
   

   $$

   $$F_ {d st} = 0,61 * 6,55 ^ 2 * 14 * ((1,17 + 0) * cos (28 * \ pi / 180) - (0,15 + 0) * sin (28 * \ pi / 180)) = 405,8 H$$
   
   Der Windwiderstand des Rumpfes verhindert eine Vorwärtsbewegung.
   

   $$

   $$R_ {fr w} = 0,61 × 6,55 × 2 × 3 × cos (28 × \ pi / 180) = 69 H$$
   
   Entsprechend der Abschleppkennlinie bestimmen wir die Geschwindigkeit $$$v_ {dp} = $ 2,7$ Knoten = 1,4 m / s
   

   $$

   $$h_ {st \ Delta cp} = 1,5 + (10 + 1,5-2 * 1,1) / 3 = 4,6 m$$
   
   $$$M_ {kr st} = 405,8 * 4,6 = 1867 N / m$ Aus dem Stabilitätsdiagramm ermitteln wir den Fersenwinkel $$$\ phi_ {ct} = 3.9 ^ o$ . Nun, das sind Kleinigkeiten, deshalb werden wir noch ein Segel hinzufügen - das Großsegel!
   Das Großsegel wirkt wie eine Klappe am Flügel eines Flugzeugs und dreht sich schräg um den Mast $$$70 ^ o$ . Der Koeffizient der aerodynamischen Verlängerung des Großsegels $$$A_ {y gr} = h_ {gr} ^ 2 / S_ {gr} = $ 4,$ ;
   optimaler Anstellwinkel $$$\ alpha_ {a} = 10 ^ o$ ; Su = 1,09; Cx = 0,15.
   Die Projektion der Kraft der Grotte auf die Längsrichtung der Yacht ist eine nützliche Kraft:
   

   $$

   $$F_ {s gr} = 0,61 * 6,55 ^ 2 * 17,2 * ((1,09 + 0) * sin (28 * \ pi / 180) - (0,15 + 0) * cos ( 28 * \ pi / 180)) = 170 H$$
   
   Die Projektion der Kraft der Grotte auf die Querrichtung der Yacht ist die Driftkraft:
   

   $$

   $$F_ {d gr} = 0,61 * 6,55 ^ 2 * 17,2 * ((1,09 + 0) * cos (28 * \ pi / 180) - (0,15 + 0) * sin ( 28 * \ pi / 180))) = 464 H$$
   
   $$$h _ {\ Sigma cpu} = 4,16 m$ , $$$M_ {kr} = 3127 H$ und Rollwinkel $$$\ phi _ {\ Sigma} = 8.5 ^ o$ .
   Gesamtvorwärtskraft:
   $$$F_ {s} = F_ {s st} + F_ {s gr} -R_ {fr w} = 153,5 + 170-69 = 254 H$ Vorwärtsgeschwindigkeit $$$v_ {dp} = $ 3.$ Knoten oder 1,86 m / s.
   Wenn wir davon ausgehen, dass der echte Wind streng nach Norden weht, zeigt der Kompass an Bord den Winkel der Längskomponente der Geschwindigkeit der Yacht an $$$\ alpha_ {vw} = 38.1 ^ o$ .
   Driftgeschwindigkeit wird sein $$$v_ {d} = 0,418 m / s$ .
   Jetzt müssen wir diese Ergebnisse in die Realität umsetzen.
   
   Der Spurwinkel der tatsächlichen Bewegung ist:
   $$$\ alpha_ {real} = atan (\ frac {v_ {d}} {v_ {dp}}) + \ alpha = atan (\ frac {0.418} {1.86}) + 38.1 = 51 ^ o$ Dies ist der Winkel des echten Windes $$$\ alpha_ {rw}$ zum Bewegungsvektor der Yacht.
   
   Und die wahre Geschwindigkeit der Bewegung im Raum: $$$v_ {real} = \ sqrt {v_ {dp} ^ 2 + v_ {d} ^ 2}$ = 1,92 + 0,4182 = 1,9 m / s.
   Echte Windgeschwindigkeit:
   $$$v_ {rw} = \ sqrt {v ^ 2 + v_ {vw} ^ 2-2 * v * v_ {vw} * cos (\ alpha_ {vw})} = 5 m / s$ .
   Unter solchen Bedingungen beträgt die Geschwindigkeit des Vorrückens streng gegen den Wind 1,2 m / s oder 2,35 Knoten, und Sie müssen sich entlang eines Zick-Zack-Weges bewegen.
   
   Nach der Berechnung für andere mögliche Winkel des Wimpelwinds können Sie ein kreisförmiges Heftdiagramm der Abhängigkeit der tatsächlichen Geschwindigkeit der Yacht vom tatsächlichen Wind erhalten. 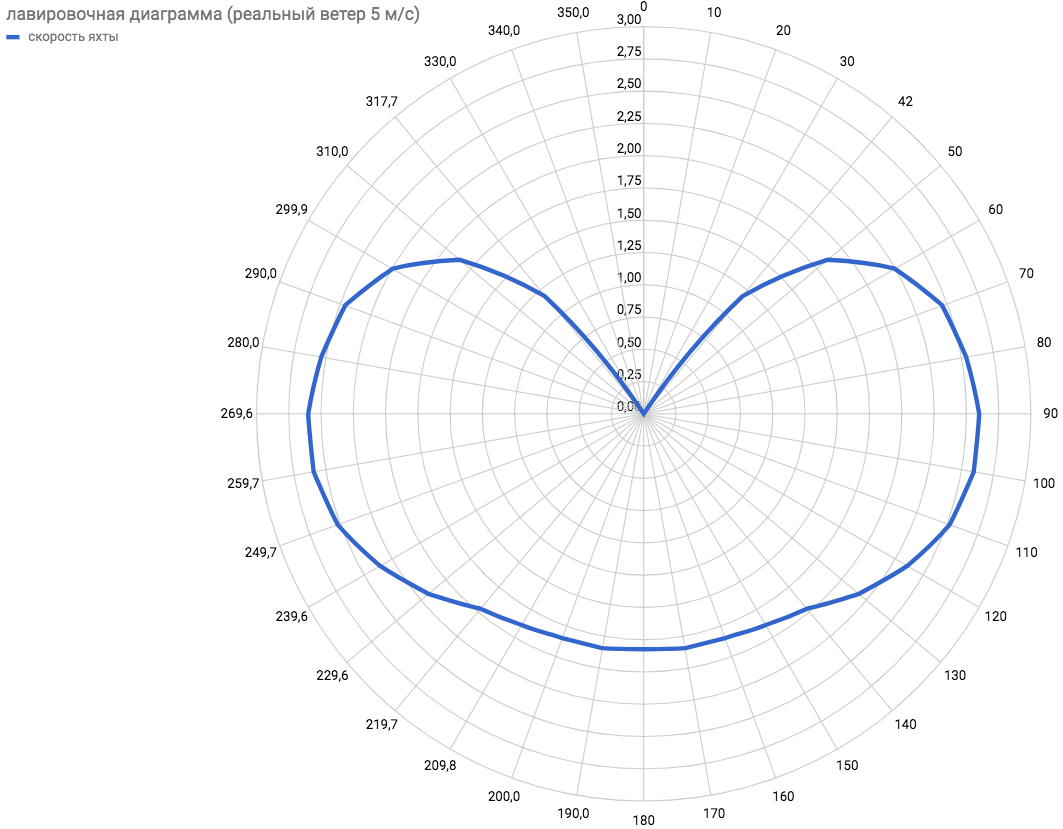Damit können Sie bereits Routen auf der Karte entsprechend der Windvorhersage planen. Darüber hinaus wurde deutlich, dass der kleinstmögliche Winkel $$$\ alpha_ {real min} = 43,5 ^ o$ und die maximale Geschwindigkeit gegen den Wind wird mit dem Steuerkurswinkel erreicht $$$50 ^ o <\ alpha_ {real} <53 ^ o$ für Wind 5 m / s.