Übersetzung eines interessanten Longreads zur Visualisierung von Konzepten aus der Informationstheorie. Im ersten Teil werden wir uns ansehen, wie Wahrscheinlichkeitsverteilungen, ihre Wechselwirkung und bedingte Wahrscheinlichkeiten grafisch dargestellt werden. Als nächstes werden wir uns mit Codes fester und variabler Länge befassen, um zu sehen, wie der optimale Code aufgebaut ist und warum. Als Ergänzung wird das statistische Paradoxon von Simpson visuell verstanden.Die Informationstheorie gibt uns eine genaue Sprache für die Beschreibung vieler Dinge. Wie viel Unsicherheit steckt in mir? Wie viel Wissen über die Antwort auf Frage A gibt mir Auskunft über die Antwort auf Frage B? Wie ähnlich ist eine Überzeugung einer anderen? Ich hatte informelle Versionen dieser Ideen, als ich ein kleines Kind war, aber die Informationstheorie kristallisiert sie in präzise, kraftvolle Ideen. Diese Ideen finden eine Vielzahl von Anwendungen, von der Datenkomprimierung über die Quantenphysik bis hin zum maschinellen Lernen und den weiten Bereichen dazwischen.
Leider kann die Informationstheorie einschüchternd wirken. Ich glaube nicht, dass es dafür einen Grund gibt. Tatsächlich können viele Schlüsselideen visuell erklärt werden!
Wahrscheinlichkeitsverteilungsvisualisierung
Bevor wir uns mit der Informationstheorie befassen, wollen wir uns überlegen, wie Sie einfache Wahrscheinlichkeitsverteilungen visualisieren können. Wir werden sie später brauchen, außerdem sind diese Techniken zur Visualisierung von Wahrscheinlichkeiten an sich nützlich!
Ich bin in kalifornien Manchmal regnet es, aber meistens die Sonne! Sagen wir, 75% der Zeit ist es sonnig. Es ist leicht auf dem Bild darzustellen:
Die meisten Tage trage ich ein T-Shirt, aber manchmal trage ich einen Regenmantel. Angenommen, ich trage 38% der Zeit einen Regenmantel. Dies ist auch leicht darzustellen.
Was ist, wenn ich beide Fakten gleichzeitig visualisieren möchte? Es ist einfach, wenn sie nicht interagieren - d. H. sind unabhängig. Zum Beispiel, wenn das so ist: Dass ich heute ein T-Shirt oder einen Regenmantel trage, hängt nicht vom Wetter nächste Woche ab. Wir können dies mit einer Achse für eine Variable und einer für die andere abbilden:
Achten Sie auf gerade vertikale und horizontale Linien. So sieht Unabhängigkeit aus! Die Wahrscheinlichkeit, dass ich einen Regenmantel trage, ändert sich nicht, da es in einer Woche regnen wird. Mit anderen Worten, die Wahrscheinlichkeit, dass ich einen Regenmantel trage und es nächste Woche regnet, ist gleich der Wahrscheinlichkeit, dass ich einen Regenmantel trage, multipliziert mit der Wahrscheinlichkeit, dass es regnet. Sie interagieren nicht.
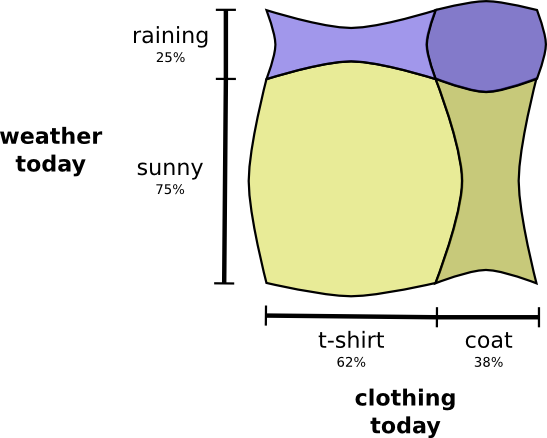
Wenn Variablen interagieren, kann sich die Wahrscheinlichkeit für einige Variablenpaare erhöhen und für andere verringern. Es ist sehr wahrscheinlich, dass ich einen Regenmantel trage und es regnet, weil die Variablen miteinander korrelieren und sich gegenseitig wahrscheinlicher machen. Es ist wahrscheinlicher, dass ich an einem regnerischen Tag einen Regenmantel trage als die Wahrscheinlichkeit, dass ich an einem Tag einen Regenmantel trage und es an einem anderen zufälligen Tag regnet.
Optisch sieht es so aus, als würden einige der Quadrate mit einer zusätzlichen Wahrscheinlichkeit anschwellen, während sich die anderen Quadrate verengen, da es unwahrscheinlich ist, dass einige Ereignisse gleichzeitig auftreten:
Aber obwohl es cool aussieht, ist es nicht sehr nützlich, um zu verstehen, was passiert.
Konzentrieren wir uns stattdessen auf eine Variable wie das Wetter. Wir kennen die Wahrscheinlichkeiten von sonnigem und regnerischem Wetter. In beiden Fällen können wir bedingte Wahrscheinlichkeiten berücksichtigen. Wie hoch ist die Wahrscheinlichkeit, dass ich ein T-Shirt trage, wenn es sonnig ist? Wie hoch ist die Wahrscheinlichkeit, dass ich bei Regen einen Regenmantel trage?
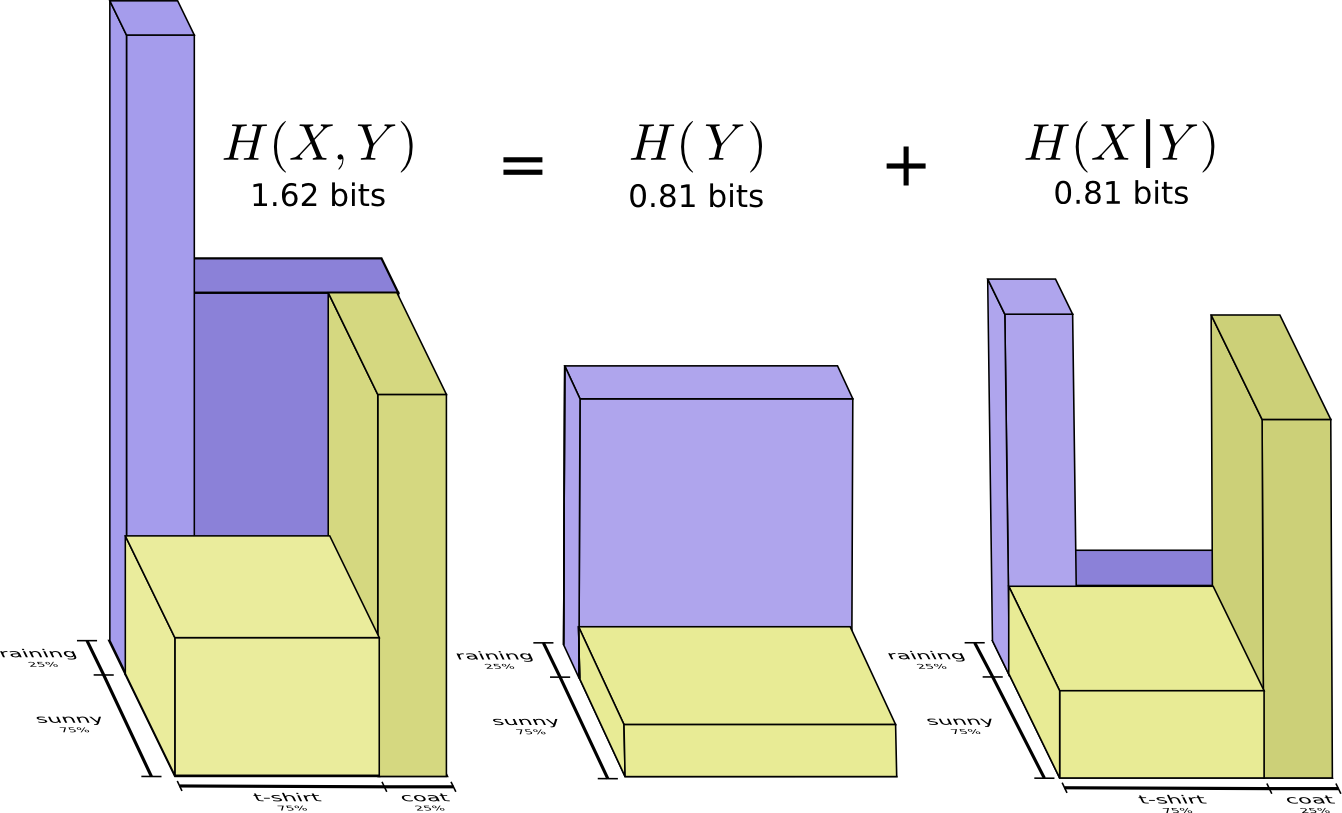
Mit einer Wahrscheinlichkeit von 25% wird es regnen. Bei Regen trage ich einen Regenmantel mit einer Wahrscheinlichkeit von 75%. Daher beträgt die Wahrscheinlichkeit, dass es regnet und ich einen Regenmantel trage, 25% von 75%, was ungefähr 19% entspricht. Die Wahrscheinlichkeit, dass es regnet und ich einen Regenmantel trage, ist die Wahrscheinlichkeit, dass es regnen wird, multipliziert mit der Wahrscheinlichkeit, dass ich bei Regen einen Regenmantel trage. Wir schreiben es so:
Dies ist ein Beispiel für eine der grundlegendsten Identitäten der Wahrscheinlichkeitstheorie:
Wir zerlegen die Distribution in ein zweiteiliges Produkt. Zunächst betrachten wir die Wahrscheinlichkeit, dass eine Variable, das Wetter, einen bestimmten Wert annimmt. Dann betrachten wir die Wahrscheinlichkeit, dass eine andere Variable, meine Klamotten, aufgrund der ersten Variable den Wert annimmt.
Mit welcher Variablen Sie beginnen, spielt keine Rolle. Wir könnten mit meinen Klamotten anfangen und uns dann das dadurch verursachte Wetter ansehen. Dies mag weniger intuitiv erscheinen, da wir verstehen, dass es einen Kausalzusammenhang zwischen dem Wetter gibt, der sich auf das auswirkt, was ich trage, und nicht umgekehrt ... aber es funktioniert trotzdem!
Schauen wir uns ein Beispiel an. Wenn wir einen zufälligen Tag wählen, werde ich mit einer Wahrscheinlichkeit von 38% einen Regenmantel tragen. Wenn wir wissen, dass ich einen Regenmantel trage, wie wahrscheinlich ist es, dass es regnet? Ich würde lieber einen Regenmantel im Regen als in der Sonne tragen, aber Regen in Kalifornien ist selten und es stellt sich heraus, dass es mit einer Wahrscheinlichkeit von 50% regnen wird. Die Wahrscheinlichkeit, dass es regnet und ich einen Regenmantel trage, ist die Wahrscheinlichkeit, dass ich einen Regenmantel trage (38%), multipliziert mit der Wahrscheinlichkeit, dass es regnet, wenn ich einen Regenmantel trage (50%) ungefähr 19%.
Dies gibt uns eine zweite Möglichkeit, die gleiche Wahrscheinlichkeitsverteilung zu visualisieren.
Bitte beachten Sie, dass die Etikettenwerte eine etwas andere Bedeutung haben als im vorherigen Diagramm: Ein T-Shirt und ein Regenmantel sind jetzt die Grenzwahrscheinlichkeiten, die Wahrscheinlichkeit, dass ich diese Kleidung tragen werde, ohne das Wetter zu berücksichtigen. Andererseits gibt es jetzt zwei Regen- und Sonnenflecken, weil ihre Wahrscheinlichkeiten davon abhängen, dass ich ein T-Shirt oder einen Regenmantel trage.
(Vielleicht haben Sie schon von Bayes 'Theorem gehört. Sie können es sich als eine Art Übergang zwischen diesen beiden verschiedenen Arten der Darstellung der Wahrscheinlichkeitsverteilung vorstellen!)
Box: Das Simpson-Paradoxon
Sind diese Visualisierungstechniken für Wahrscheinlichkeitsverteilungen wirklich nützlich? Ich denke ja! Ein wenig weiter verwenden wir sie, um die Informationstheorie zu visualisieren, aber im Moment verwenden wir sie, um das Simpson-Paradoxon zu studieren. Das Simpson-Paradoxon ist eine äußerst unintuitive statistische Situation. Es ist auf einer intuitiven Ebene schwer zu verstehen. Michael Nielsen hat einen ausgezeichneten Aufsatz
Reinventing Explanation verfasst , der das Paradoxon auf vielfältige Weise erklärt. Ich möchte versuchen, es selbst zu tun, indem ich die Techniken verwende, die wir im vorherigen Abschnitt entwickelt haben.
Zwei Methoden zur Behandlung von Nierensteinen werden getestet. Die Hälfte der Patienten erhält die Behandlung A, während die andere Hälfte die Behandlung B erhält. Patienten, die die Behandlung B erhalten haben, erholten sich mit größerer Wahrscheinlichkeit als Patienten, die die Behandlung A erhalten haben.
Patienten mit kleinen Nierensteinen erholten sich jedoch eher, wenn sie die Behandlung A erhielten. Patienten mit großen Nierensteinen in der Niere erholten sich ebenfalls eher, wenn sie die Behandlung A erhielten! Wie kann das sein?
Das Problem besteht im Wesentlichen darin, dass die Studie nicht ordnungsgemäß randomisiert wurde. Unter den Patienten, die die Behandlung A erhielten, gab es mehr Patienten mit großen Nierensteinen, und unter den Patienten, die die Behandlung B erhielten, gab es mehr Patienten mit kleinen Nierensteinen.
Wie sich herausstellt, erholen sich Patienten mit kleinen Nierensteinen im Allgemeinen viel eher.
Um dies besser zu verstehen, können wir die beiden vorherigen Diagramme kombinieren. Das Ergebnis ist ein dreidimensionales Diagramm mit einer Wiederfindungsrate, die in kleine und große Nierensteine unterteilt ist.
Jetzt sehen wir, dass sowohl bei kleinen als auch bei großen Steinen die Behandlung A der Behandlung B überlegen ist. Die Behandlung B sah nur deshalb besser aus, weil die Patienten, bei denen sie angewendet wurde, im Allgemeinen mehr Heilungschancen hatten!
Codes
Da wir nun Möglichkeiten haben, die Wahrscheinlichkeit zu visualisieren, können wir in die Informationstheorie eintauchen.
Lassen Sie sich von meinem imaginären Freund Bob erzählen. Bob liebt Tiere sehr. Er redet ständig über Tiere. Tatsächlich spricht er nur vier Wörter: "Hund", "Katze", "Fisch" und "Vogel".
Vor ein paar Wochen zog er trotz der Tatsache, dass Bob eine Erfindung meiner Vorstellungskraft war, nach Australien. Außerdem entschied er, dass er nur im Binärformat kommunizieren wollte. Alle meine (imaginären) Nachrichten von Bob sehen so aus:
Um zu kommunizieren, müssen Bob und ich ein Codierungssystem erstellen - eine Möglichkeit, Wörter in einer Folge von Bits anzuzeigen.
Um eine Nachricht zu senden, ersetzt Bob jedes Zeichen (Wort) durch das entsprechende Codewort und kombiniert sie dann zu einer codierten Zeichenfolge.
Codes mit variabler Länge
Leider sind Kommunikationsdienste im imaginären Australien teuer. Ich muss 5 US-Dollar für jede Nachricht bezahlen, die ich von Bob erhalte. Habe ich erwähnt, dass Bob gerne viel redet? Um nicht pleite zu gehen, beschlossen Bob und ich herauszufinden, ob es möglich war, die durchschnittliche Nachrichtenlänge irgendwie zu reduzieren.
Es stellt sich heraus, dass Bob nicht alle Wörter gleich oft ausspricht. Bob liebt Hunde sehr. Er spricht die ganze Zeit über Hunde. Manchmal spricht er über andere Tiere - besonders über eine Katze, die sein Hund gerne jagt - aber meistens spricht er über Hunde. Hier ist ein Diagramm der Häufigkeit seiner Worte:
Das ist ermutigend. Unser alter Code verwendet 2-Bit-Codewörter, egal wie oft sie verwendet werden.
Es gibt eine gute Möglichkeit, dies zu visualisieren. Im folgenden Diagramm verwenden wir die vertikale Achse, um die Wahrscheinlichkeit jedes Wortes zu visualisieren
und eine horizontale Achse zur Visualisierung der Länge des entsprechenden Codeworts
. Bitte beachten Sie, dass der resultierende Bereich die durchschnittliche Länge des von uns gesendeten Codeworts ist, in diesem Fall 2 Bits.
Wir können schlauer sein und den Code in der Länge variabel machen, wobei Codewörter für gebräuchliche Wörter kürzer gemacht werden. Das Problem ist, dass es einen Wettbewerb zwischen Codewörtern gibt - einige werden kürzer, andere müssen länger werden. Um die Länge der Nachricht zu minimieren, möchten wir, dass alle Codewörter kurz sind, aber die kürzeste sollte weit verbreitet sein. Daher enthält der resultierende Code kürzere Codewörter für gebräuchliche Wörter (z. B. "Hund") und längere Codewörter für seltene Wörter (z. B. "Vogel").
Stellen wir uns das noch einmal vor. Bitte beachten Sie, dass die häufigsten Codewörter kürzer und die seltensten länger sind. Infolgedessen haben wir eine kleinere Fläche. Dies entspricht einer kürzeren erwarteten Codewortlänge. Die durchschnittliche Codewortlänge beträgt jetzt 1,75 Bit!
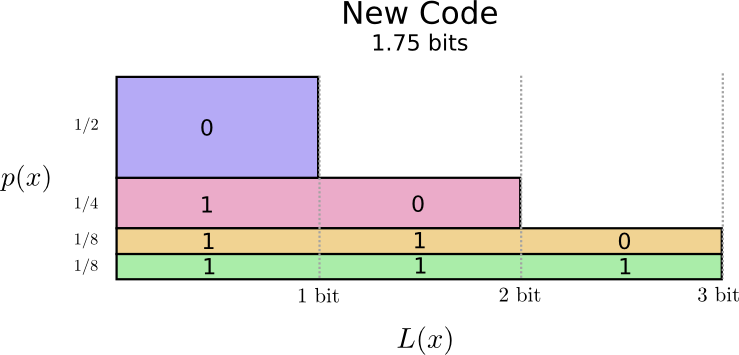
(Sie fragen sich vielleicht: Warum nicht 1 separat als Codewort verwenden? Leider führt dies zu Mehrdeutigkeiten beim Decodieren von codierten Zeichenfolgen. Wir werden später darauf näher eingehen.)
Es stellt sich heraus, dass dieser Code der bestmögliche ist. Für diese Verteilung gibt es keinen Code, der eine durchschnittliche Codewortlänge von weniger als 1,75 Bit ergibt.
Es gibt eine grundlegende Grenze. Für die Übertragung des gesagten Wortes und des Ereignisses dieser Verteilung müssen durchschnittlich mindestens 1,75 Bit übertragen werden. Egal wie intelligent unser Code sein mag, es ist unmöglich zu erreichen, dass die durchschnittliche Nachrichtenlänge geringer ist. Wir nennen diese fundamentale Grenze die
Verteilungsentropie - wir werden sie im Folgenden genauer diskutieren.
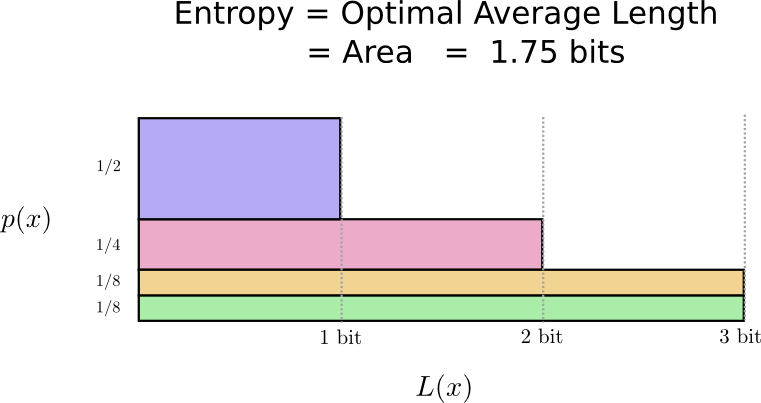
Wenn wir diese Grenze verstehen wollen, müssen wir den Kompromiss zwischen kurzen und langen Codewörtern verstehen. Sobald wir das herausgefunden haben, können wir herausfinden, wie die bestmöglichen Codierungssysteme aussehen.
Codewortraum
Es gibt zwei Codewörter mit einer Länge von 1 Bit: 0 und 1. Es gibt vier Codewörter mit einer Länge von 2 Bits: 00, 01, 10 und 11. Jedes hinzugefügte Bit verdoppelt die Anzahl der möglichen Codewörter.
Wir interessieren uns für Codes mit variabler Länge, bei denen einige Codewörter länger sind als andere. Wir können einfache Situationen haben, wenn wir acht Codewörter haben, die 3 Bits lang sind. Es kann komplexere Mischungen geben, zum Beispiel zwei Codewörter der Länge 2 und vier Codewörter der Länge 3. Was entscheidet darüber, wie viele Codewörter unterschiedlicher Länge wir haben können?
Denken Sie daran, dass Bob seine Nachrichten in verschlüsselte Zeichenfolgen umwandelt, jedes Wort durch seinen Code ersetzt und sie verkettet.
Bei der Erstellung von Codes mit variabler Länge ist eine subtile Frage zu beachten. Wie teilen wir die codierte Zeichenfolge wieder in Codewörter auf? Wenn alle Codewörter die gleiche Länge haben, ist es einfach - teilen Sie die Zeichenfolge einfach in Stücke dieser Länge auf. Da es aber Codewörter unterschiedlicher Länge gibt, müssen wir auf den Inhalt achten.
Wir möchten, dass unser Code eindeutig dekodierbar ist. Und wir möchten nicht, dass es nicht eindeutig ist, aus welchen Codewörtern die codierte Zeichenfolge besteht. Wenn wir ein spezielles Symbol "Ende des Codeworts" hätten, wäre es einfach. Aber das haben wir nicht - wir senden nur 0 und 1. Wir müssen in der Lage sein, die Sequenz der Codewörter zu betrachten und zu bestimmen, wo jedes von ihnen endet.
Es ist sehr einfach, Codes zu erstellen, die nicht eindeutig entschlüsselt werden können. Stellen Sie sich zum Beispiel vor, dass 0 und 01 beide Codewörter sind. Dann ist unklar, was das erste Codewort der Zeile 0100111 ist - es kann entweder dies oder das sein! Die Eigenschaft, die wir benötigen, ist, dass wenn wir ein bestimmtes Codewort sehen, es nicht in einem anderen, längeren Codewort enthalten sein sollte. Mit anderen Worten sollte kein Codewort ein Präfix eines anderen Codeworts sein. Dies wird als Präfix-Eigenschaft bezeichnet, und die Codes, die dieser Eigenschaft folgen, werden als
Präfix-Codes bezeichnet .
Ein nützlicher Weg, dies darzustellen, besteht darin, dass jedes Codewort Opfer aus dem Raum möglicher Codewörter erfordert. Wenn wir das Codewort 01 nehmen, verlieren wir die Fähigkeit, Codewörter zu verwenden, deren Präfix es ist. Wir können 010 oder 011010110 wegen der Mehrdeutigkeit nicht mehr verwenden - sie gehen uns verloren.
Da ein Viertel aller Codewörter um 01 beginnt, haben wir ein Viertel aller möglichen Codewörter gespendet. Hier ist der Preis, den wir dafür bezahlen, dass wir ein Codewort mit einer Länge von nur 2 Bits haben! Dieses Opfer bedeutet wiederum, dass alle anderen Codewörter etwas länger sein sollten. Es gibt immer eine Art Kompromiss zwischen den Längen verschiedener Codewörter. Ein kurzes Codewort erfordert, dass Sie den größten Teil des Platzes möglicher Codewörter opfern, was die Kürze anderer Codewörter verhindert. Was wir herausfinden müssen, ist, wie man richtig kompromittiert!
Optimale Kodierung
Sie können es sich als ein begrenztes Budget vorstellen, das Sie für kurze Codewörter ausgeben können. Wir bezahlen für ein Codewort und opfern einen Teil der möglichen Codewörter.
Der Kauf eines Codeworts der Länge 0 kostet 1 - alle möglichen Codewörter - Wenn Sie ein Codewort der Länge 0 haben möchten, können Sie kein anderes Codewort haben. Die Kosten für ein Codewort mit einer Länge von 1, beispielsweise "0", betragen 1/2, da die Hälfte der möglichen Codewörter mit "0" beginnen. Die Kosten für ein Codewort der Länge 2, beispielsweise "01", betragen 1/4, da ein Viertel aller möglichen Codewörter mit "01" beginnt. Im Allgemeinen nehmen die Kosten für Codewörter mit zunehmender Länge des Codeworts exponentiell ab.
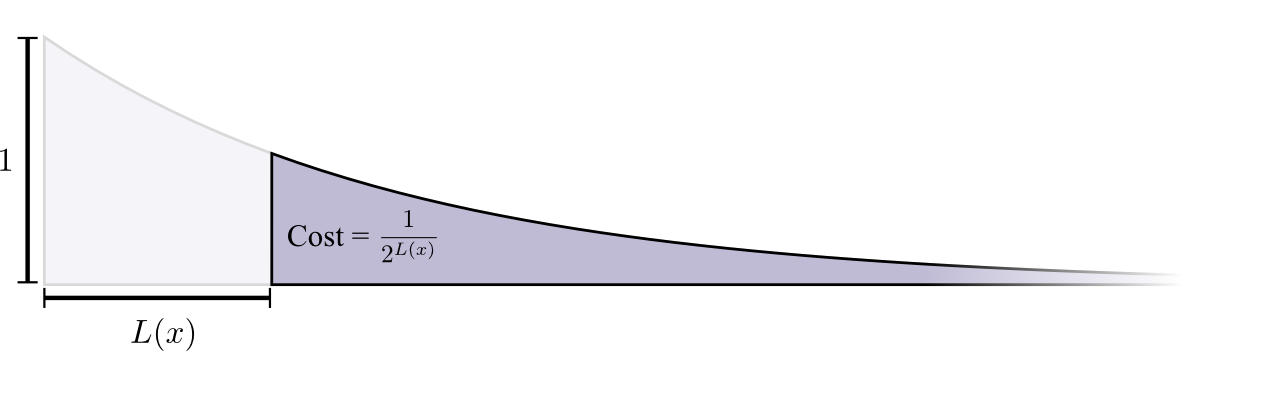
Bitte beachten Sie: Wenn die Kosten für einen (Sach-) Aussteller sinken, ist dies sowohl Höhe als auch Fläche! (
Im Beispiel wurde ein Exponent mit der Basis 2 verwendet, bei dem diese Tatsache falsch ist. Sie können jedoch zum natürlichen Exponenten wechseln, was den Beweis visuell vereinfacht. )
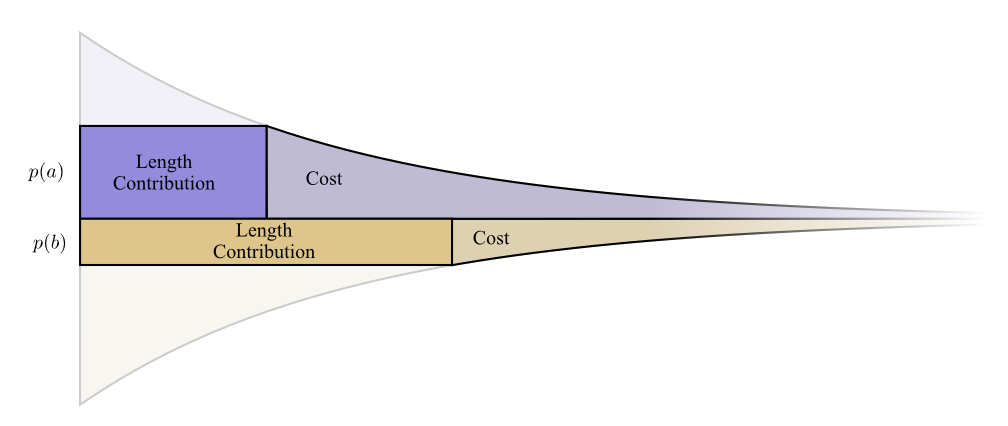
Wir brauchen kurze Codewörter, weil wir die durchschnittliche Nachrichtenlänge reduzieren wollen. Jedes Codewort erhöht die durchschnittliche Nachrichtenlänge um die Wahrscheinlichkeit des Wortes multipliziert mit seiner Länge. Wenn wir beispielsweise in 50% der Fälle ein Codewort mit einer Länge von 4 Bit senden müssen, ist unsere durchschnittliche Nachrichtenlänge 2 Bit länger als ohne dieses Codewort. Wir können uns das als Rechteck vorstellen.
Diese beiden Werte hängen mit der Codewortlänge zusammen. Der Preis, den wir zahlen, bestimmt die Länge des Codeworts. Die Länge des Codeworts bestimmt, wie viel es zur durchschnittlichen Länge der Nachricht beiträgt. Wir können sie uns so zusammen vorstellen.
Kurze Codewörter verringern die durchschnittliche Nachrichtenlänge, sind jedoch teuer, während lange Codewörter die durchschnittliche Nachrichtenlänge erhöhen, jedoch billig sind.
Wie können Sie unser begrenztes Budget am besten nutzen? Wie viel sollten wir für jedes Ereignis für ein Codewort ausgeben?
So wie eine Person mehr in Tools investieren möchte, die sie regelmäßig verwendet, möchten wir auch mehr für häufig verwendete Codewörter ausgeben. Es gibt einen besonders natürlichen Weg, dies zu tun: Verteilen Sie unser Budget im Verhältnis zu der Häufigkeit, mit der die Veranstaltung stattfindet. Wenn ein Ereignis in 50% der Fälle eintritt, geben wir 50% unseres Budgets für den Kauf eines kurzen Codeworts dafür aus. Wenn das Ereignis jedoch nur 1% der Zeit auftritt, geben wir nur 1% unseres Budgets aus, da wir uns keine großen Sorgen über die Länge des Codeworts machen.
Das ist eine ziemlich natürliche Sache, aber ist es optimal? Das ist so, und ich werde es beweisen!
Der folgende Beweis ist klar und sollte verstanden werden, aber es wird einige Arbeit erfordern, um es herauszufinden, und dies ist definitiv der schwierigste Teil dieses Aufsatzes. Der Leser kann es ohne Bedenken überspringen und die Tatsache ohne Beweise akzeptieren und mit dem nächsten Abschnitt fortfahren.Schauen wir uns ein konkretes Beispiel an, in dem wir feststellen müssen, welches der beiden möglichen Ereignisse eingetreten ist. Ereignis und
.
Die Grenzen von Kosten und Länge reihen sich wunderbar aneinander. Bedeutet das etwas?Überlegen Sie, was mit dem Beitrag von Kosten und Länge geschieht, wenn wir die Länge des Codeworts ein wenig ändern. Wenn wir die Länge des Codeworts geringfügig erhöhen, nimmt der Beitrag der Nachrichtenlänge proportional zu ihrer Höhe an der Grenze zu, und die Kosten nehmen proportional zu ihrer Höhe an der Grenze ab.
Die Kosten für die Erstellung eines kürzeren Codeworts betragen somit .
Wir sind nicht gleichermaßen besorgt über die Länge jedes Codeworts, sie interessieren uns im Verhältnis zu der Häufigkeit, mit der wir sie verwenden. Im Fall von .
Unser Gewinn durch die Verkürzung des Codeworts ist proportional .
Interessanterweise sind beide Ableitungen gleich. Dies bedeutet, dass unser ursprüngliches Budget eine interessante Funktion hat: Wenn Sie etwas mehr Geld hätten, wäre es ebenso gut, in die Reduzierung eines Codeworts zu investieren. Was uns wirklich am Herzen liegt, ist das Kosten-Nutzen-Verhältnis - genau das entscheidet, in was wir mehr investieren sollten. In diesem Fall ist das Verhältnis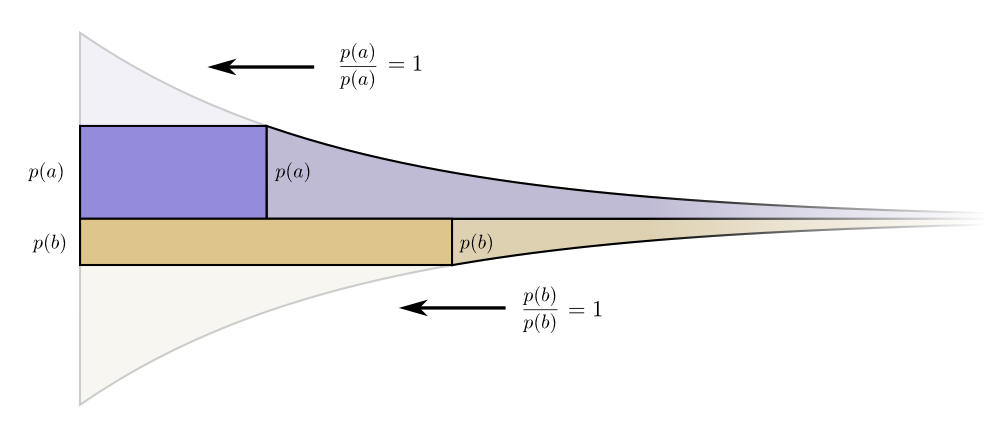
.
Es macht ein Codewort für .
Die Vorteile sind jedoch die gleichen. Dies führt dazu, dass das Kosten-Nutzen-Verhältnis für den Einkauf stimmt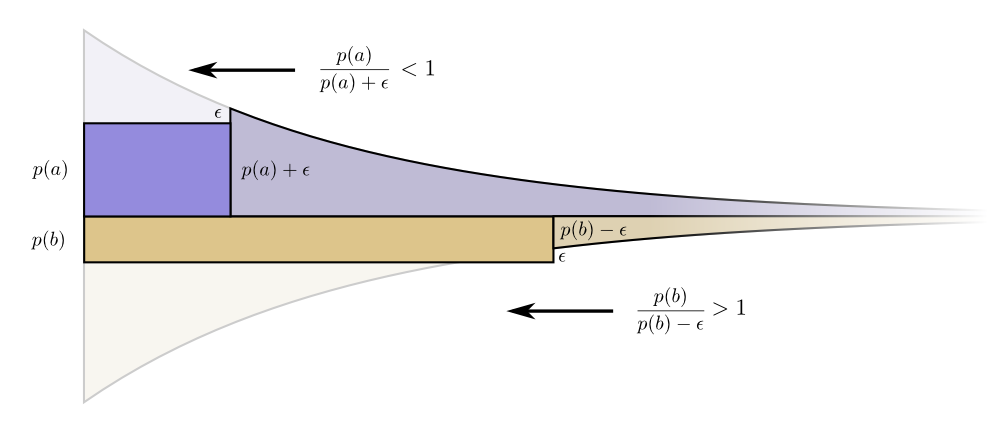
.
Investoren schreien: "Kaufen !
Verkaufen (Ein aufmerksamer Leser hat möglicherweise bemerkt, dass bei einem optimalen Budget möglicherweise Codes mit gebrochenen Codewörtern angezeigt werden. Was bedeutet dies? Wenn Sie in der Praxis mit einem einzigen Codewort kommunizieren möchten, müssen Sie den Wert runden. Aber wie machen wir das? siehe später, es ist wirklich sinnvoll, gebrochene Codewörter zu senden, wenn wir viele davon gleichzeitig senden!)PS Die Fortsetzung ist Entropie, Kreuzentropie, gegenseitige Information, gebrochene Bits und anderen interessanten Dingen gewidmet.