SVM Erklärung von Grund auf neu und Implementierung in Python. Detaillierte Analyse der Support-Vektor-Methode

Hallo an alle, die den Weg des ML-Samurai gewählt haben!

Einleitung:

In diesem Artikel betrachten wir die Support Vector Machine- Methode ( engl. SVM, Support Vector Machine ) für das Klassifizierungsproblem. Die Hauptidee des Algorithmus wird vorgestellt, die Ausgabe der Gewichtseinstellung und eine einfache DIY-Implementierung werden analysiert. Am Beispiel eines Datensatzes $$$Iris$Der Betrieb des geschriebenen Algorithmus mit linear trennbaren / untrennbaren Daten im Raum wird demonstriert $$$R ^ 2$und Visualisierung von Training / Prognose. Zusätzlich werden die Vor- und Nachteile des Algorithmus und seiner Modifikationen bekannt gegeben.

Abbildung 1. Open Source-Foto einer Irisblume

Das zu lösende Problem:

Wir werden das Problem der binären Klassifikation (wenn es nur zwei Klassen gibt) lösen. Erstens trainiert der Algorithmus Objekte aus dem Trainingssatz, für die Klassenbeschriftungen im Voraus bekannt sind. Ferner sagt der bereits trainierte Algorithmus die Klassenbezeichnung für jedes Objekt aus der verzögerten / Testprobe voraus. Klassenbeschriftungen können Werte annehmen $$$Y = \ {- 1, +1 \}$ . Objekt - Vektor mit N Zeichen $$$x = (x_1, x_2, ..., x_n)$im Weltraum $$$R ^ n$. Beim Lernen sollte der Algorithmus eine Funktion aufbauen $$$F (x) = y$Das braucht ein Argument $$$x$- ein Objekt aus dem Weltraum $$$R ^ n$und gibt das Klassenetikett $$$y$.

Allgemeine Wörter über den Algorithmus:

Die Klassifizierungsaufgabe bezieht sich auf den Unterricht bei einem Lehrer. SVM ist ein Lernalgorithmus mit einem Lehrer. Visuell finden Sie in diesem erstklassigen Artikel viele Algorithmen für maschinelles Lernen (siehe Abschnitt „Karte der Welt des maschinellen Lernens“). Es sollte hinzugefügt werden, dass SVM auch für Regressionsprobleme verwendet werden kann, aber der SVM-Klassifikator wird in diesem Artikel analysiert.

Das Hauptziel von SVM als Klassifikator ist es, die Gleichung einer trennenden Hyperebene zu finden
$$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 = 0$im Weltraum $$$R ^ n$, was die beiden Klassen auf eine optimale Weise trennen würde. Gesamtansicht der Transformation $$$F$Einrichtung $$$x$zum Klassenlabel $$$Y$: $$$F (x) = Vorzeichen (w ^ Tx-b)$. Wir werden uns erinnern, dass wir bezeichnet haben $$$w = (w_1, w_2, ..., w_n), b = -w_0$. Nach dem Einrichten des Algorithmus Gewichte $$$w$und $$$b$(Training) werden alle Objekte, die auf eine Seite der konstruierten Hyperebene fallen, als erste Klasse und Objekte, die auf die andere Seite fallen - die zweite Klasse, vorhergesagt.

Innenfunktion $$$sign ()$Es gibt eine lineare Kombination von Merkmalen des Objekts mit den Algorithmusgewichten, weshalb SVM auf lineare Algorithmen verweist. Eine teilende Hyperebene kann auf verschiedene Arten konstruiert werden, jedoch in SVM-Gewichten $$$w$und $$$b$sind so konfiguriert, dass Klassenobjekte so weit wie möglich von der trennenden Hyperebene entfernt liegen. Mit anderen Worten, der Algorithmus maximiert die Lücke ( englischer Rand ) zwischen der Hyperebene und den Klassenobjekten, die ihm am nächsten liegen. Solche Objekte werden Stützvektoren genannt (siehe Abb. 2). Daher der Name des Algorithmus.

Abbildung 2. SVM (die Basis der Abbildung von hier )

Eine detaillierte Ausgabe der SVM-Skalenanpassungsregeln:

Um die Teilungshyperebene so weit wie möglich von den Abtastpunkten entfernt zu halten, sollte die Streifenbreite maximal sein. Vektor $$$w$Ist der Richtungsvektor der teilenden Hyperebene. Nachfolgend bezeichnen wir das Skalarprodukt zweier Vektoren als $$$\ langle a, b \ rangle$oder $$$a ^ Tb$Suchen wir die Projektion des Vektors, dessen Enden die Stützvektoren verschiedener Klassen sind, auf den Richtungsvektor der Hyperebene. Diese Projektion zeigt die Breite des Trennstreifens (siehe Abb. 3):

Abbildung 3. Die Ausgabe der Regeln zum Einstellen der Skalen (die Grundlage der Abbildung von hier )

Der Rand des Objekts x von der Klassengrenze ist der Wert $$$M = y (w ^ Tx-b)$. Der Algorithmus macht genau dann einen Fehler am Objekt, wenn der Einzug aktiviert ist $$$M$negativ (wenn $$$y$und $$$(w ^ Tx-b)$verschiedene Charaktere). Wenn $$$M ∈ (0, 1)$Dann fällt das Objekt in den Trennstreifen. Wenn $$$M> 1$wird das Objekt x korrekt klassifiziert und befindet sich in einiger Entfernung vom Trennstreifen. Wir schreiben diesen Zusammenhang auf:

Das resultierende System ist die Standard- SVM- Einstellung mit einer SVM mit festem Rand , wenn kein Objekt in das Trennungsband eintreten darf. Es wird analytisch durch das Kuhn-Tucker-Theorem gelöst. Das resultierende Problem entspricht dem doppelten Problem, den Sattelpunkt der Lagrange-Funktion zu finden.

$$$$ display $$ \ left \ {\ begin {array} {ll} (w ^ Tw) / 2 \ rightarrow min & \ textrm {} \\ y (w ^ Tx-b) \ geqslant 1 & \ textrm {} \ end {array} \ right. $$ display $$

All dies ist gut, solange unsere Klassen linear trennbar sind. Lassen Sie uns unser System ein wenig transformieren, damit der Algorithmus mit linear untrennbaren Daten arbeiten kann. Lassen Sie den Algorithmus Fehler an den Trainingsobjekten machen, aber versuchen Sie gleichzeitig, weniger Fehler zu vermeiden. Wir führen eine Reihe zusätzlicher Variablen ein $$$\ xi _i> 0$Charakterisierung der Größe des Fehlers bei jedem Objekt $$$x_i$. Wir führen eine Strafe für den Gesamtfehler in die minimierte Funktion ein:

$$$$ display $$ \ left \ {\ begin {array} {ll} (w ^ Tw) / 2 + \ alpha \ sum \ xi _i \ rightarrow min & \ textrm {} \\ y (w ^ Tx_i-b) \ geqslant 1 - \ xi _i & \ textrm {} \\ \ xi _i \ geqslant0 & \ textrm {} \ end {array} \ right. $$ display $$

Wir betrachten die Anzahl der Algorithmusfehler (wenn M <0 ist). Nenne es Strafe . Dann entspricht die Strafe für alle Objekte der Höhe der Geldbußen für jedes Objekt $$$x_i$wo $$$[M_i <0]$- Schwellenwertfunktion (siehe Abb. 4):

$$$$ display $$ [M_i <0] = \ left \ {\ begin {array} {ll} 1 & \ textrm {if} M_i <0 \\ 0 & \ textrm {if} M_i \ geqslant 0 \ end {array} \ right. $$ display $$

Als nächstes machen wir die Strafe empfindlich für die Größe des Fehlers und führen gleichzeitig eine Strafe für die Annäherung des Objekts an die Klassengrenze ein:

Beim Hinzufügen des Begriffs zum Strafausdruck $$$\ alpha (w ^ Tw) / 2$Wir erhalten die klassische SVM- Verlustfunktion mit weicher Lücke ( soft-margin SVM ) für ein Objekt:

$$$Q$- Verlustfunktion, es ist auch eine Verlustfunktion. Das minimieren wir mit Hilfe des Gradientenabfalls bei der Umsetzung der Hände. Wir leiten die Regeln für das Ändern von Gewichten ab, wo $$$\ eta$- Abstiegsstufe:

$$$$ display $$ \ bigtriangledown Q = \ left \ {\ begin {array} {ll} \ alpha w-yx & \ textrm {if} yw ^ Tx <1 \\ \ alpha w & \ textrm {if} yw ^ Tx \ geqslant 1 \ end {array} \ right. $$ display $$

Mögliche Fragen bei Interviews (basierend auf realen Ereignissen):

Nach allgemeinen Fragen zu SVM: Warum maximiert Hinge_loss den Abstand? - Denken Sie zunächst daran, dass eine Hyperebene ihre Position ändert, wenn sich die Gewichte ändern $$$w$und $$$b$. Die Gewichte des Algorithmus beginnen sich zu ändern, wenn die Gradienten der Verlustfunktion ungleich Null sind (sie sagen normalerweise: "Gradientenfluss"). Deshalb haben wir speziell eine solche Verlustfunktion gewählt, bei der zum richtigen Zeitpunkt Gradienten zu fließen beginnen. $$$Scharnierverlust$sieht so aus: $$$H = max (0,1-y (w ^ Tx))$. Denken Sie daran, dass die Freigabe $$$m = y (w ^ Tx)$. Wenn die Lücke $$$m$groß genug ( $$$1$oder mehr) Ausdruck $$$(1-m)$wird kleiner als Null und $$$H = 0$(Daher fließen keine Gradienten, und das Gewicht des Algorithmus ändert sich in keiner Weise.) Wenn die Lücke m ausreichend klein ist (zum Beispiel, wenn das Objekt in das Trennband fällt und / oder negativ ist (wenn die Klassifizierungsvorhersage falsch ist), wird Hinge_loss positiv ( $$$H> 0$) beginnen Gradienten zu fließen und die Algorithmusgewichte ändern sich. Zusammenfassung: Gradienten fließen in zwei Fällen: wenn das Probenobjekt in das Trennband fiel und wenn das Objekt falsch klassifiziert ist.

Um das Niveau einer Fremdsprache zu überprüfen, sind ähnliche Fragen möglich: Was sind die Ähnlichkeiten und Unterschiede zwischen LogisticRegression und SVM? - Zunächst werden wir über Ähnlichkeiten sprechen: Beide Algorithmen sind lineare Klassifizierungsalgorithmen beim überwachten Lernen. Einige Ähnlichkeiten bestehen in ihren Argumenten für Verlustfunktionen: $$$log (1 + exp (-y (w ^ Tx)))$für logreg und $$$max (0,1-y (w ^ Tx))$für SVM (siehe Bild 4). Beide Algorithmen können mit Gradientenabstieg konfiguriert werden. Als nächstes wollen wir uns mit den Unterschieden befassen: SVM gibt die Klassenbezeichnung des Objekts zurück, im Gegensatz zu LogReg, das die Wahrscheinlichkeit einer Klassenmitgliedschaft zurückgibt. SVM kann nicht mit Klassenbeschriftungen arbeiten $$$\ {0,1 \}$ (ohne Klassen umzubenennen) im Gegensatz zu LogReg (LogReg-Verlustfinktion für $$$\ {0,1 \}$ : $$$-ylog (p) - (1-y) log (1-p)$wo $$$y$- Echtes Klassenlabel, $$$p$- Rückkehr des Algorithmus, Wahrscheinlichkeit der Zugehörigkeit zu einem Objekt $$$x$zum unterricht $$$\ {1 \}$ ) Darüber hinaus können wir das Problem der margenschwachen SVM ohne Gradientenabnahme lösen. Die Suche nach Hilfsvektoren wird in der Lagrange-Funktion auf den Suchsattelpunkt reduziert - diese Aufgabe bezieht sich nur auf die quadratische Programmierung.

import numpy as np import matplotlib.pyplot as plt %matplotlib inline xx = np.linspace(-4,3,100000) plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0') plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)') plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)') plt.title('Loss = F(Margin)') plt.grid() plt.legend(prop={'size': 14}); 

Abbildung 4. Verlustfunktionen

Einfache Implementierung von klassischem Soft-Margin-SVM:

Achtung! Einen Link zum vollständigen Code finden Sie am Ende des Artikels. Unten finden Sie Codeblöcke, die aus dem Kontext genommen wurden. Einige Bausteine ​​können erst nach dem Ausarbeiten der vorherigen Bausteine ​​gestartet werden. Unter vielen Blöcken werden Bilder platziert, die zeigen, wie der darüber platzierte Code funktioniert.

 import numpy as np import warnings warnings.filterwarnings('ignore') import matplotlib.pyplot as plt import matplotlib.lines as mlines plt.rcParams['figure.figsize'] = (8,6) %matplotlib inline from sklearn.datasets import load_iris from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split def newline(p1, p2, color=None): #    #function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib ax = plt.gca() xmin, xmax = ax.get_xbound() if(p2[0] == p1[0]): xmin = xmax = p1[0] ymin, ymax = ax.get_ybound() else: ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0]) ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0]) l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color) ax.add_line(l) return l 

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended class CustomSVM(object): __class__ = "CustomSVM" __doc__ = """ This is an implementation of the SVM classification algorithm Note that it works only for binary classification ############################################################# ###################### PARAMETERS ###################### ############################################################# etha: float(default - 0.01) Learning rate, gradient step alpha: float, (default - 0.1) Regularization parameter in 0.5*alpha*||w||^2 epochs: int, (default - 200) Number of epochs of training ############################################################# ############################################################# ############################################################# """ def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) def predict(self, X:np.array) -> np.array: y_pred = [] X_extended = add_bias_feature(X) for i in range(len(X_extended)): y_pred.append(np.sign(np.dot(self._w,X_extended[i]))) return np.array(y_pred) def hinge_loss(self, x, y): return max(0,1 - y*np.dot(x, self._w)) def soft_margin_loss(self, x, y): return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w) 

Wir betrachten im Detail die Funktionsweise jedes Zeilenblocks:

1) Erstelle eine Funktion add_bias_feature (a) , die automatisch den Vektor von Objekten erweitert und die Zahl 1 an das Ende jedes Vektors anfügt , um den freien Term „zu vergessen“. B. Ausdruck $$$w ^ Tx-b$äquivalent zum Ausdruck $$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 * 1$. Wir gehen davon aus, dass die Einheit die letzte Komponente des Vektors für alle Vektoren x und x ist $$$w_0 = -b$. Stellen Sie nun die Gewichte ein $$$w$und $$$w_0$Wir werden zur gleichen Zeit produzieren.

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended 

2) Dann werden wir den Klassifikator selbst beschreiben. Es hat die Funktionen, init () zu initialisieren, fit () zu lernen, predict () vorherzusagen , den Verlust der Funktion hinge_loss () zu ermitteln und den Gesamtverlust der Funktion des klassischen Algorithmus mit einer weichen Lücke soft_margin_loss () zu ermitteln .

3) Bei der Initialisierung werden 3 Hyperparameter eingeführt: _etha - Schritt des Gradientenabfalls ( $$$\ eta$), _α - Geschwindigkeitskoeffizient der proportionalen Gewichtsreduktion (vor dem quadratischen Term in der Verlustfunktion $$$\ alpha$), _epochs - die Anzahl der Trainingsperioden.

  def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None 

4) Während des Trainings für jede Ära der Trainingsstichprobe (X_train, Y_train) wird ein Element aus der Stichprobe genommen und der Abstand zwischen diesem Element und der Position der Hyperebene zu einem bestimmten Zeitpunkt berechnet. Abhängig von der Größe dieser Lücke ändern wir das Gewicht des Algorithmus unter Verwendung des Gradienten der Verlustfunktion $$$Q$. Gleichzeitig berechnen wir den Wert dieser Funktion für jede Epoche und wie oft wir die Gewichte pro Epoche ändern. Bevor wir mit dem Training beginnen, werden wir sicherstellen, dass nicht mehr als zwei verschiedene Klassenlabels in die Lernfunktion aufgenommen wurden. Vor dem Einrichten der Waage wird diese mit der Normalverteilung initialisiert.

  def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) 

Überprüfung der Funktionsweise des geschriebenen Algorithmus:

Überprüfen Sie, ob unser schriftlicher Algorithmus mit einer Art Spielzeugdatensatz funktioniert. Nehmen Sie den Iris-Datensatz. Wir werden die Daten aufbereiten. Bezeichnen Sie die Klassen 1 und 2 als $$$+ 1$und Klasse 0 als $$$-1$. Mit dem PCA-Algorithmus (Erklärung und Anwendung hier ) reduzieren wir den Platz von 4 Attributen optimal auf 2 bei minimalem Datenverlust (es wird uns leichter fallen, das Training und das Ergebnis zu beobachten). Als nächstes werden wir in eine Trainings- (Zug-) Probe und eine verzögerte (Validierungs-) Probe unterteilen. Wir werden die Trainingsstichprobe trainieren, sie vorhersagen und prüfen. Wir wählen die Lernfaktoren so, dass die Verlustfunktion sinkt. Während des Trainings werden wir uns mit der Verlustfunktion des Trainings und der verzögerten Probenahme befassen.

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

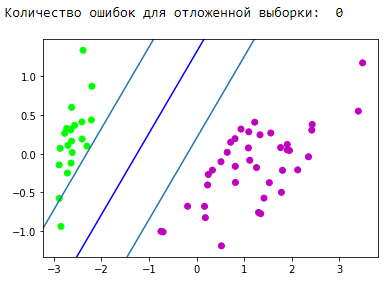
Großartig! Unser Algorithmus handhabte linear trennbare Daten. Nun trennen Sie die Klassen 0 und 1 von der Klasse 2:

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors[:150]) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

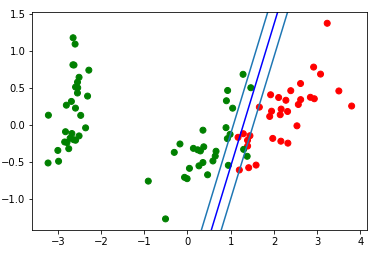
Schauen wir uns das GIF an, das zeigt, wie sich die Position der Trennlinie während des Trainings geändert hat (nur 500 Frames für das Ändern der Gewichte. Die ersten 300 in einer Reihe. Die nächsten 200 Stück für jedes 130. Frame):

 import matplotlib.animation as animation from matplotlib.animation import PillowWriter def one_image(w, X, Y): axes = plt.gca() axes.set_xlim([-4,4]) axes.set_ylim([-1.5,1.5]) d1 = {-1:'green', 1:'red'} im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y]) im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue') # im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1 # im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 return im fig = plt.figure() ims = [] for i in range(500): if i<=300: k = i else: k = (i-298)*130 im = one_image(svm.history_w[k], X_train, Y_train) ims.append([im]) ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True, repeat_delay=500) writer = PillowWriter(fps=20) ani.save("my_demo.gif", writer='imagemagick') 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

Räume begradigen

Es ist wichtig zu verstehen, dass es bei realen Problemen keinen einfachen Fall mit linear trennbaren Daten gibt. Um mit solchen Daten zu arbeiten, wurde die Idee vorgeschlagen, in einen anderen Raum zu ziehen, in dem die Daten linear getrennt werden können. Ein solcher Raum heißt gleichrichten. Das Korrigieren von Leerzeichen und Kerneln ist in diesem Artikel nicht betroffen. Die vollständigste mathematische Theorie finden Sie in der Zusammenfassung von E. Sokolov und in den Vorlesungen von K.V. Vorontsov .

Verwenden von SVM aus sklearn:

Tatsächlich sind fast alle klassischen Algorithmen für maschinelles Lernen für Sie geschrieben. Lassen Sie uns ein Beispiel für den Code geben. Wir werden den Algorithmus aus der sklearn- Bibliothek entnehmen .

 from sklearn import svm from sklearn.metrics import recall_score C = 1.0 # = self._alpha in our algorithm model1 = svm.SVC(kernel='linear', C=C) #model1 = svm.LinearSVC(C=C, max_iter=10000) #model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C) #model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C) model1.fit(X_train, Y_train) y_predict = model1.predict(X_test) print(recall_score(Y_test, y_predict, average=None)) 

Vor- und Nachteile der klassischen SVM:

Vorteile:

1. funktioniert gut mit großem Funktionsraum;
2. funktioniert gut mit kleinen Daten;
3. Der Algorithmus ermittelt also, dass das Teilungsband maximiert wird, wodurch sich wie bei einem Airbag die Anzahl der Klassifizierungsfehler verringern lässt.
4. Da sich der Algorithmus darauf reduziert, das quadratische Programmierproblem in einem konvexen Bereich zu lösen, hat ein solches Problem immer eine eindeutige Lösung (die Trennungs-Hyperebene mit bestimmten Hyperparametern des Algorithmus ist immer dieselbe).

Nachteile:

1. lange Einarbeitungszeit (für große Datenmengen);
2. Lärminstabilität: Ausreißer in Trainingsdaten werden zu Referenzobjekten für Eindringlinge und wirken sich direkt auf die Konstruktion einer trennenden Hyperebene aus.
3. allgemeine Methoden zur Konstruktion von Kerneln und zur Korrektur von Räumen, die für ein bestimmtes Problem bei linearer Untrennbarkeit von Klassen am besten geeignet sind, werden nicht beschrieben. Das Auswählen nützlicher Datentransformationen ist eine Kunst.

SVM-Anwendung:

Die Wahl des einen oder anderen Algorithmus für maschinelles Lernen hängt direkt von den Informationen ab, die beim Data Mining erhalten werden. Generell lassen sich folgende Aufgaben unterscheiden:

• Aufgaben mit einem kleinen Datensatz;
• Textklassifizierungsaufgaben. SVM liefert eine gute Ausgangsbasis ([Vorverarbeitung] + [TF-iDF] + [SVM]), die resultierende Prognosegenauigkeit liegt auf dem Niveau einiger faltungsbedingter / wiederkehrender neuronaler Netze (ich empfehle, diese Methode selbst auszuprobieren, um das Material zu konsolidieren). Ein hervorragendes Beispiel finden Sie hier, "Teil 3. Ein Beispiel für einen der von uns gelehrten Tricks" ;
• für viele Aufgaben mit strukturierten Daten der Link [Feature-Engineering] + [SVM] + [Kernel] "noch Kuchen";
• Da der Scharnierverlust als ziemlich schnell angesehen wird, kann er in Vowpal Wabbit (standardmäßig) gefunden werden.

Algorithmusänderungen:

Es gibt verschiedene Ergänzungen und Modifikationen der Support-Vektor-Methode, um bestimmte Nachteile zu beseitigen:

• Relevanz-Vektor-Maschine (RVM)
• 1-Norm-SVM (LASSO-SVM)
• Doppelt regulierte SVM (ElasticNet SVM)
• Support Features Machine (SFM)
• Relevanzmerkmale Maschine (RFM)

Zusätzliche Quellen zu SVM:

1. Textvorträge von K.V. Vorontsov
2. Zusammenfassungen von E. Sokolov - 14.15.16
3. Coole Quelle von Alexandre Kowalczyk
4. Auf einem habr gibt es 2 Artikel, die SVM gewidmet sind:
   
   • 2010 Jahr
   • 2018 Jahr
5. Auf dem Github kann ich unter den folgenden Links 2 coole SVM-Implementierungen hervorheben:
   
   • MLAlgorithmen von einem inländischen Entwickler
   • ML-From-Scratch

Fazit:

Vielen Dank für Ihre Aufmerksamkeit! Für Kommentare, Feedback und Tipps wäre ich dankbar.
Sie finden den vollständigen Code aus diesem Artikel auf meinem Github .

ps Danke yorko für Tipps zum Glätten von Ecken. Vielen Dank an Aleksey Sizykh - eine Abteilung für Physik und Technologie, die teilweise in den Code investiert hat.