Guten Tag!
Wie in meinem ersten Artikel versprochen, möchte ich Sie mit einer der Methoden zum Lösen des Systems der diophantinischen Gleichungen vertraut machen. Ziel des Artikels ist es, andere Leser mit dieser Technik vertraut zu machen und sie mehr oder weniger verständlich zu vermitteln.
Betrachten Sie ein System aus zwei diophantinischen Gleichungen
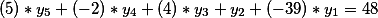
und

Wir finden alle möglichen Lösungen für die erste Gleichung. Wie, fragst du? Sicher gibt es verschiedene Methoden, aber ich werde in einem der folgenden Artikel beschreiben, wie ich ein ähnliches Problem lösen kann. Nun nehmen wir nur an, dass die allgemeine Lösung die Form hat

Wie kann ich überprüfen, ob ich nicht lüge?
Es genügt, sich an die Matrixrechnung zu erinnern und den Wertevektor unserer ersten diophantinischen Gleichung (ohne freien Term) mit der Matrix aller Koeffizienten zu multiplizieren .

Als Ergebnis erhält man den Wert des freien Terms, und daher sind die Berechnungen korrekt
Der nächste Schritt ist die Substitution unserer gemeinsamen Lösung.

in die zweite Gleichung

Das Verfahren ist dasselbe: Wir multiplizieren den Vektor aus den Koeffizienten der zweiten Gleichung mit der allgemeinen Lösung der ersten
Wir bekommen dieses Ergebnis
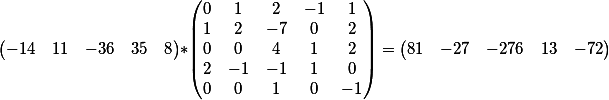
Das heißt, wir haben eine Gleichung der Form
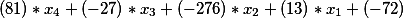
Auf der rechten Seite der zweiten diophantinischen Gleichung blieb, da es einen freien Term von -335 gab, dieser übrig, das heißt, unsere endgültige Lösung hat zu diesem Zeitpunkt die Form
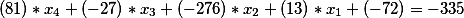
Oder wir bewegen die freien Mitglieder nach rechts
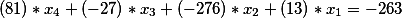
Also haben wir die nächste diophantinische Gleichung. Lassen Sie uns die allgemeine Lösung finden und auf die Wahrheit prüfen.

das heißt, die allgemeine Lösung ist
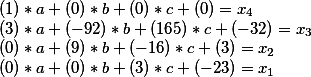
Und jetzt machen wir die inverse Transformation (lass es so heißen). Das ist das System

Anstelle des unbekannten x ersetzen wir das, was in der letzten Phase passiert ist
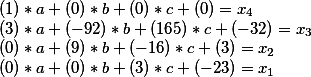
In der Matrixrechnung wird dies gelöst, indem eine Matrix mit einer anderen multipliziert wird.
Bei der ersten Matrix muss jedoch eine bestimmte Prozedur ausgeführt werden: Entfernen Sie (vorübergehend) die letzte Spalte mit freien Begriffen, da dieser Parameter nicht an der Multiplikation teilnimmt und später verwendet wird.
Das Ergebnis der Multiplikation zweier Matrizen wird erzeugt
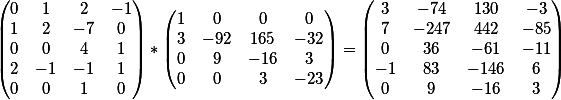
die Matrix
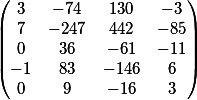
Die letzte Spalte enthält die freien Mitglieder dieses Systems.
Wir berücksichtigen die Spalte, die vor der Multiplikation vorübergehend gelöscht wurde, und fügen sie hinzu
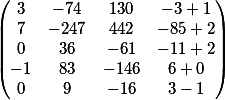
unsere endgültige Antwort in Matrixform
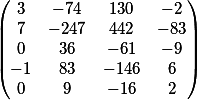
Probieren Sie es aus?
Das Vektorprodukt der Koeffizienten der ersten Gleichung und der Matrix
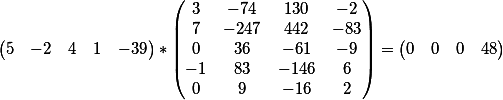
und das Vektorprodukt der Koeffizienten der zweiten Gleichung und der Matrix
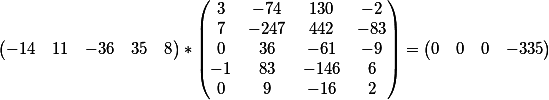
Wie Sie sehen, stimmt das Ergebnis mit dem freien Term jeder der Gleichungen überein.
Somit hat die allgemeine Lösung die Form
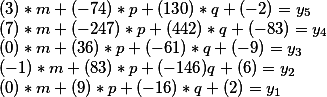
wobei m, p, q - beliebige ganzzahlige Werte annehmen kann
Auf solch einfache Weise ist es möglich, komplexere lineare Diophantingleichungen zu lösen. Im Anschluss an diesen Algorithmus wurde ein echter Taschenrechner erstellt, der es wirklich nicht mag, wenn anstelle der Werte in den Koeffizienten der ersten Gleichung des Anfangssystems Nullen auftreten. Dies ist jedoch ein Problem meiner spezifischen Implementierung dieses Algorithmus.
Im nächsten Thema erkläre ich Ihnen, wie Sie mit der Matrix der allgemeinen Lösung Diophantingleichungen erstellen. Die Aufgabe ist in der Regel banal und wird in einer Handlung erledigt, aber plötzlich weiß es jemand nicht mehr.
Für Kommentare, Rückmeldungen und Vorschläge wäre ich dankbar.