Seit Jahrhunderten suchen Forscher nach Beispielen für Situationen, in denen sich die Euler-Gleichungen für die Hydrodynamik eines idealen Fluids als falsch herausstellen. Und schließlich fanden Mathematiker ein solches Beispiel.
Mathematiker haben jahrelang vermutet, dass
die Euler-Gleichungen unter bestimmten Bedingungen nicht funktionieren werden. Sie konnten jedoch nicht das spezifische Szenario beschreiben, in dem dies auftritt. Bis heute
Diese Gleichungen sind eine idealisierte mathematische Beschreibung der Flüssigkeitsbewegung. Unter bestimmten Voraussetzungen modellieren sie die Ausbreitung von Wellen auf einem Teich oder die Infiltration von Melasse aus einer Dose. Sie sollten in der Lage sein, die Bewegung jeder Flüssigkeit unter allen Bedingungen zu beschreiben - und das über mehr als zwei Jahrhunderte hinweg.
Neue Erkenntnisse belegen jedoch, dass diese Gleichungen unter bestimmten Bedingungen immer noch nicht funktionieren.
"Vor anderthalb Jahren hätte ich nicht
gedacht , dass ich eine solche Entwicklung schon zu Lebzeiten
erleben würde ", sagte
Tarek Elgindi , Mathematiker an der Universität von Kalifornien in San Diego, der Autor eines neuen Werks.
Elgindi hat die Existenz von Fehlern in den Euler-Gleichungen in zwei Werken nachgewiesen, die 2019 in Zusammenarbeit mit
Tejeddin Gole und
Nader Masmudi veröffentlicht wurden - er selbst schrieb
April und
Oktober . Die Arbeit drehte sich um ein Jahrhundert von Annahmen über diese berühmten Gleichungen für Flüssigkeiten.
"Ich denke, das ist eine wunderbare und wunderbare Leistung", sagte
Peter Constantine , Mathematiker an der Princeton University.
Elgindis Arbeit läutet nicht das Ende von Eulers Gleichungen ein. Es beweist, dass sich die Gleichungen unter ganz bestimmten Bedingungen zu überhitzen scheinen und anfangen, Unsinn zu verbreiten. Unter realistischeren Bedingungen bleiben die bisherigen Gleichungen jedoch unverwundbar.
Die von Elgindi festgestellte Ausnahme überraschte die Mathematiker jedoch, da sie unter Bedingungen auftritt, unter denen, wie zuvor angenommen, die Gleichung ohnehin funktionieren sollte.
"Im Allgemeinen scheint es mir, dass die Menschen von dem Beispiel von Tarek überrascht sind", sagte
Vlad Vikol , Mathematiker an der New York University.
Wie die Euler-Gleichungen schnellten
Leonhard Euler leitete die Gleichungen für Flüssigkeiten ab, die 1757 seinen Namen tragen. Sie beschreiben die Entwicklung einer Flüssigkeit im Laufe der Zeit, so wie Newtons Gleichungen die Bewegung einer Billardkugel auf einem Tisch beschreiben.
Genauer gesagt bezeichnen diese Gleichungen die augenblickliche Bewegung von infinitesimalen Teilchen einer Flüssigkeit. Ihre Beschreibung beinhaltet die Geschwindigkeit des Partikels (wie schnell und in welche Richtung es sich bewegt) und eine solche Größe wie die
Vorticity (wie schnell sich das Partikel nach Art einer Spitze dreht und in welche Richtung).
Alle diese Informationen bilden ein „Geschwindigkeitsfeld“, eine Momentaufnahme der Flüssigkeitsbewegung zu einem bestimmten Zeitpunkt. Euler-Gleichungen beginnen mit dem anfänglichen Geschwindigkeitsfeld und sagen voraus, wie sich dieses zu einem späteren Zeitpunkt ändern wird.
Tarek ElgindiEuler-Gleichungen beschreiben die Flüssigkeit der realen Welt nicht wörtlich. Dazu gehören mehrere nicht-physische Annahmen. Zum Beispiel funktionieren sie nur, wenn interne Strömungen in der Flüssigkeit keine Reibung erzeugen und sich relativ zueinander bewegen. Es wird auch von einer Inkomprimierbarkeit von Flüssigkeiten ausgegangen, dh nach den Regeln der Euler-Gleichungen ist es unmöglich, eine Flüssigkeit zu komprimieren, wenn sie in einem Raum mit geringerem Volumen angeordnet ist, als es bereits erforderlich ist.
"Dieses Modell kann man sich als idealisierte Welt vorstellen und Gleichungen als Regeln für die Bewegung dieser Welt", schrieb
Vladimir Sverak von der University of Minnesota per E-Mail an uns.
Diese ungewöhnlichen Umstände ließen den Mathematiker und Physiker John von Neumann scherzhaft feststellen, dass diese Gleichungen das Verhalten von „trockenem Wasser“ simulieren. Um eine realistischere Flüssigkeit zu simulieren, die innere Reibung (die sogenannte Viskosität) erfährt, verwenden
die Forscher
die Navier-Stokes-Gleichungen .
„Eulers Gleichungen sind sehr idealisiert. Reibung ist in echten Flüssigkeiten vorhanden “, sagte Konstantin.
Gleichzeitig nehmen die Euler-Gleichungen in der Wissenschaft immer noch einen angesehenen Platz ein. Die Forscher möchten wissen, ob diese Gleichungen im Rahmen dieser idealisierten Welt ohne Reibung und Kompression klar funktionieren, dh ob sie alle zukünftigen Zustände aller möglichen Anfangsversionen von Geschwindigkeitsfeldern beschreiben können. Oder mit anderen Worten: Gibt es eine solche fließende Bewegung, die diese Gleichungen nicht modellieren können?
"Im Kern ist die Frage einfach: Machen diese Gleichungen immer ihre Arbeit?", Sagte Sverak.
Wenn Sie in den Gleichungen die Werte des aktuellen Zustands der Flüssigkeit einsetzen, erhalten Sie theoretisch die genauen Werte, um den zukünftigen Zustand der Flüssigkeit zu beschreiben. Dann können Sie diese neuen Werte wieder in die Gleichungen einsetzen und Ihre Prognose erweitern. Und normalerweise kann ein ähnlicher Prozess für eine beliebige Zeitspanne in der Zukunft fortgesetzt werden.
Es ist jedoch auch möglich, dass unter sehr seltenen Bedingungen die Gleichungen brechen. Sie können knarren, pusten, Ausgabewerte erzeugen, die für die Rolle zukünftiger Eingabeparameter geeignet sind, und dann plötzlich einen Wert erzeugen, der für sie überhaupt nicht geeignet ist. In solchen Fällen sagen Mathematiker, dass die Gleichungen "gehetzt" haben.
Wenn Eulers Gleichungen schnell voranschreiten, liegt das daran, dass sie die Geschwindigkeit oder Verwirbelung des Punktes auf unnatürliche Weise erhöhen. Dieser Gewinn wird so stark sein, dass in einer endlichen Zeit die Geschwindigkeit oder der Wirbel eines Punktes unendlich wird. Und sobald die Gleichungen einen unendlichen Wert ergeben, werden sie zusammenbrechen und in Zukunft keine Umgebungsbedingungen mehr beschreiben. Dies liegt daran, dass es in der Regel unmöglich ist, Berechnungen mit unendlichen Werten durchzuführen - dies entspricht der Division durch Null (im Übrigen übersteigen die Geschwindigkeitswerte in diesem Fall die Lichtgeschwindigkeit - obwohl dies in der idealisierten Welt des Modells nicht die schlechteste ist).
Diese schicksalhaften unendlichen Bedeutungen werden "Singularitäten" genannt. Wenn Mathematiker fragen: "Funktionieren Euler-Gleichungen immer?", Fragen sie tatsächlich: "Gibt es Szenarien, in denen Euler-Gleichungen Singularitäten ergeben?"
Viele Mathematiker glauben, dass es gibt - bisher konnten sie jedoch kein bestimmtes Szenario finden, in dem die Gleichungen wirklich explodieren.
"Es gab das Gefühl, dass Euler versuchte, die Singularität zu vermeiden, und bis vor kurzem gelang es ihm", sagte Konstantin.
Die neue Arbeit zeigt nicht, wie Gleichungen Singularitäten unter Bedingungen ergeben, an denen Mathematiker am meisten interessiert sind. Bisher ist dieses Ergebnis dem Ziel jedoch näher gekommen als der Rest. Und dafür betrachtete Elgindi ein vereinfachtes Modell der Flüssigkeitsbewegung.
Komplexität reduzieren
Mathematiker haben viele verschiedene Möglichkeiten, die Komplexität der Flüssigkeitsbewegung zu reduzieren, für deren Simulation sie die Euler-Gleichungen verwenden. Viele der interessantesten Ergebnisse, die denen von Elgindi ähneln, beinhalten eine Demonstration, wie sehr Sie das Verhalten der Flüssigkeit vereinfachen können - das heißt, wie sehr Sie die in die Gleichungen eingegebenen Daten vereinfachen können - und dennoch die Möglichkeit haben, etwas Bedeutendes über die Gleichungen selbst zu sagen.
In einer realen dreidimensionalen Flüssigkeit, wie z. B. Wasser in einem Teich, hat jedes Partikel drei mögliche Bewegungsachsen: die x-Achse (links und rechts), die y-Achse (oben und unten) und die z-Achse (hin und her). Sehr viel Bewegungsfreiheit. Darüber hinaus ist die Bewegung von Partikeln in einem Teil der Flüssigkeit nicht unbedingt stark mit der Bewegung von Partikeln in einem anderen Teil verbunden.
"Man muss zu viel im Auge behalten", sagte Elgindi.
In der neuen Arbeit vereinfacht Elgindi die Arbeit für Euler-Gleichungen. Es ist erforderlich, dass die Flüssigkeit entlang der z-Achse symmetrisch ist, was in realen Flüssigkeiten normalerweise nicht der Fall ist. Aufgrund der Symmetrie wird es einfacher, das Geschwindigkeitsfeld zu berechnen, da bekannt ist, dass die Punkte auf beiden Seiten der z-Achse spiegelsymmetrisch sind. Wenn Sie also die Geschwindigkeit oder Vorticity eines Punktes kennen, müssen Sie nur das Vorzeichen dieser Werte ändern und diese Werte für einen anderen Punkt abrufen.
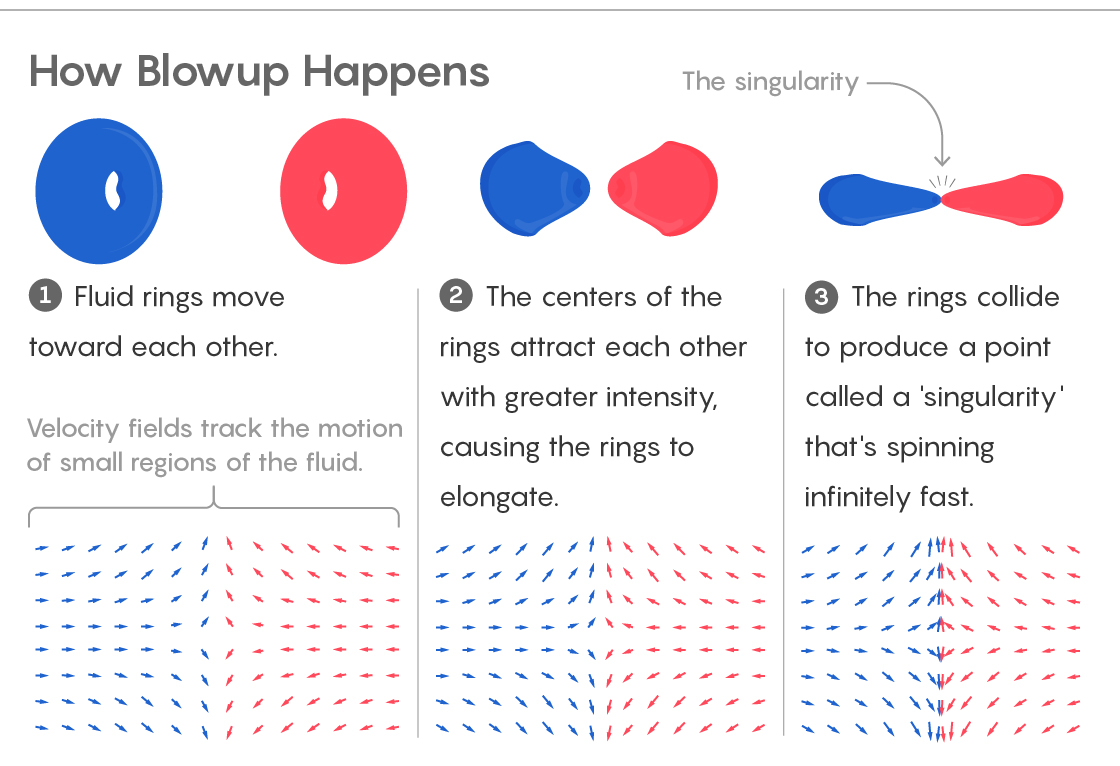1) Flüssigkeiten bewegen sich in Richtung. Geschwindigkeitsfelder verfolgen die Bewegung kleiner Flüssigkeitsabschnitte.
2) Die Zentren der Ringe werden angezogen, wodurch sich die Ringe dehnen.
3) Die Ringe kollidieren und erzeugen einen Punkt der "Singularität", der sich mit unendlicher Geschwindigkeit dreht.Es begrenzt auch die mögliche Bewegung von Punkten in der Flüssigkeit. Partikel können entweder entlang der z-Achse oder von dieser weg oder darauf zu bewegt werden. Sie können sich nicht um die z-Achse drehen. Mathematiker sagen, dass es in solchen Flüssigkeiten keine Strudel gibt.
"Dies reduziert die Aufgabe auf zweidimensional", sagte Elgindi.
Schließlich legt Elgindi den in die Euler-Gleichungen eingeführten Anfangsdaten einige weitere Bedingungen auf. In gewissem Sinne sind diese Daten rauer als diejenigen, die reale Flüssigkeiten beschreiben, und erhöhen die Wahrscheinlichkeit der Bildung von Singularitäten.
Wenn Sie sich im wirklichen Leben von einem Punkt zu einem anderen bewegen, der sich ganz in der Nähe befindet, sind die Geschwindigkeiten dieser beiden Punkte nahezu gleich. Die Wirbel dieser beiden Punkte sollten ebenfalls sehr ähnlich sein. Mathematiker sagen, dass Geschwindigkeitsfelder mit dieser Eigenschaft „glatt“ sind, dh die Werte auf ihnen ändern sich allmählich - oder gleichmäßig -, wenn sie sich von einem Punkt zum anderen bewegen. Keine schnellen Änderungen.
Aber bei der Beschreibung der Flüssigkeit von Elgindi ist alles anders.
"Die Wendung in Tareks Daten kann sich sehr ändern", sagte Vikol. "Nahe Punkte können sehr unterschiedliche Wirbel haben."
Es mag den Anschein haben, dass die Vereinfachungen von Elgindi sehr stark vom Verhalten echter Flüssigkeiten abweichen, um nützlich zu sein. Sie sind jedoch immer noch viel weniger starr als viele der vereinfachten Szenarien, in denen Wissenschaftler zuvor die Euler-Gleichungen betrachtet haben. Tatsächlich hat Elgindi sogar gezeigt, dass die Euler-Gleichungen unter diesen vereinfachten, aber nicht zu starken Bedingungen zu sehr unerwarteten Ergebnissen führen.
Das Spiel ist beendet
Stellen Sie sich einen Wasserbehälter vor, um die Entdeckung von Elgindi zu verstehen. Dies ist kein genaues Beispiel, da Elgindis Arbeit Flüssigkeiten ohne Grenzen betrachtet, die wie eine Blase in der Schwerelosigkeit fliegen. Um das Drehbuch zu visualisieren, das im Mittelpunkt seiner Arbeit steht, ist es jedoch hilfreich, das Wasser im Tank anzuordnen. Obwohl die wichtigsten mathematischen Hypothesen - und diejenigen, die am schwierigsten zu beweisen sind - Flüssigkeiten ohne Grenzen betreffen.
Stellen Sie sich zwei dicke Wasserringe an verschiedenen Enden des Tanks vor. Sie bilden kleine Trichter, wie z. B. Whirlpools - organisierte Störungen in der Flüssigkeit. Ähnliche Phänomene treten in der Natur auf und ähneln Rauchringen, die erfahrene Raucher abgeben können.
Stellen Sie sich nun vor, wie zwei entgegengesetzte Ringe zusammenkommen.
Während der Annäherung arbeiten die Euler-Gleichungen normal und zählen die Geschwindigkeitsfelder, die die Flüssigkeit zu jedem Zeitpunkt beschreiben. Aber wenn sie nahe genug beieinander liegen, führen die Gleichungen zu sehr merkwürdigen Ergebnissen.
Sie zeigen, wie sich die Ringe immer mehr anziehen - und die Mittelpunkte der Ringe noch mehr als die Außenteile. Infolgedessen werden die Ringe verlängert und beginnen, einem Trichter zu ähneln. Und je näher die Zentren der Ringe rücken, desto schneller werden sie. Und dann kollidieren sie.
Und wenn Sie in diesem Moment das Geschwindigkeitsfeld betrachten, das die Kollision beschreibt, können Sie sehen, dass mit dieser Menge von Annahmen in der gesamten Geschichte der Euler-Gleichungen niemand etwas gesehen hat: die Singularität. Elgindi bewies, dass die Euler-Gleichungen am Kollisionspunkt unendlich schnell sind. Das Spiel ist beendet.
"Die klassische Form der Gleichung bricht", sagte Elgindi. "Danach ist nicht klar, was los ist."
Das Ergebnis hat seine Grenzen. Es ist nämlich unmöglich, das Verhalten der Euler-Gleichungen unter vollständig "glatten" Bedingungen auf der Grundlage dieses Ergebnisses zu extrapolieren. Mathematiker haben vor einigen Jahrzehnten bewiesen, dass das von Elgindi betrachtete Szenario unter "glatten" Bedingungen keine Singularität hervorbringen wird.
Der Rest seines Ergebnisses verändert jedoch völlig die Sichtweise der Mathematiker auf diese alten Gleichungen.
Vor Elgindis Arbeit konnten Mathematiker keine Situation in einer Flüssigkeit ohne Grenzen nachweisen, in der die Euler-Gleichungen für einige Zeit (während die Ringe zusammenkommen) funktionieren, aber nicht unendlich. In allen früheren Arbeiten haben Mathematiker herausgefunden, dass Gleichungen immer funktionieren, wenn sie grundsätzlich funktionieren.
"Dies ist ein sehr bemerkenswertes Ergebnis, da es das Vorhandensein von Singularitäten in dem Szenario beweist, das wir als" korrekt definiert "bezeichnen." Es macht Sinn, aber gleichzeitig kommen wir in einer endlichen Zeit zu einer Singularität “, sagte Konstantin.
Viele Generationen von Wissenschaftlern haben nach einer Schwachstelle in Eulers Gleichungen gesucht. Und schließlich - mit einigen Vorbehalten - fand ihn der Mathematiker.