Über die geometrische Bedeutung von Gray-Codes

Gray-Codes sind eng mit der Hilbert-Kurve verwandt .

Bei der Kommunikation mit Kollegen stellte sich jedoch heraus, dass diese einfache Sucht in ihren Augen etwas nicht Triviales ist. Eine Internetrecherche ohne weiteres ergab im Wiki nur einen trüben Satz: „Hilbert-Kurven in Räumen größerer Dimension sind Repräsentanten von Verallgemeinerungen von Gray-Codes“. Daher bestand der Wunsch, das Thema kurz und in einfacher Sprache zu eröffnen.

Infolgedessen unter dem Schnitt - "Skandale, Intrigen, Ermittlungen".

Das Hauptmerkmal des Gray-Codes ist, dass sich zwei lexikografisch benachbarte Werte nur in einer Kategorie unterscheiden. Andererseits ist die Hilbert-Kurve stetig - der Abstand zwischen zwei benachbarten Punkten ist immer eins. Dies allein deutet auf ihre innere Verbindung hin.

Der Gray-Code beschreibt das Auftreten einer Hilbert-Kurve innerhalb eines einzelnen Hyperwürfels. Wenn wir einen 3-Bit-Code nehmen und ihn im 3-dimensionalen Raum zeichnen (wobei wir jedes Bit für die entsprechende Koordinate nehmen), erhalten wir


Abbildung 1 3-Bit-Gray-Code als dreidimensionaler Würfel

Das bekannte Bild ist das 3-dimensionale Simplex der Hilbert-Kurve! Ersetzen wir nacheinander jeden Knoten des Simplex durch denselben Simplex (unter Berücksichtigung von Rotationen und Reflexionen, um die Kontinuität aufrechtzuerhalten), erhalten wir eine Hilbert-Kurve 4x4x4.

Wenn Sie diese Iterationen fortsetzen, können Sie kontinuierlich ein beliebig großes kubisches Gitter füllen.


Abbildung 2 mehrere Iterationen des Simplex der Hilbert-Kurve.

Aber wie ist es passiert?

Es ist bekannt, dass der Gray-Code selbstähnlich ist. Es wird manchmal als Spiegel bezeichnet, weil die erste Hälfte der Werte beim Ändern der Reihenfolge mit Ausnahme des High-Bits der zweiten Hälfte entspricht. Das höchstwertige Bit wird einfach invertiert. “ Der Klarheit halber ist der 3-Bit-Code das höchstwertige Bit - ganz links:



Da es sich um Selbstähnlichkeit handelt, beginnen wir von vorne - mit einem Ein-Bit-Code. Streng genommen wäre es möglich, mit einer Nulldimension zu beginnen - Punkte, das ändert grundsätzlich nichts, nur Worte müssten mehr geschrieben werden.

Gray's einstelliger Code ist noch einfacher als ein dreizeiliges Gewehr, er ist entweder 0 oder 1.

Geometrisch entspricht dies einem eindimensionalen Einheitswürfel - einem Segment. Sie können sich entlang eines Segments entweder von Anfang bis Ende oder von Ende bis Anfang bewegen - bis zur Symmetrie ist dies ein und dasselbe. Wir werden den Anfang jedoch als den Ort bezeichnen, an dem der Wert kleiner ist (denken Sie daran, dass die Seiten des Würfels Ziffern der Zahl sind), und das Ende als den Ort, an dem der Wert größer ist.

Wir wenden uns dem zweidimensionalen Fall zu. Ein zweidimensionaler Würfel ist ein Quadrat. Unter Berücksichtigung der Selbstähnlichkeit klonen wir den eindimensionalen Würfel (0,1) und erhalten zwei Segmente - (0,0 -> 1,0) und (0,1 -> 1,1). Jetzt müssen Sie diese Segmente verbinden, um das Quadrat zu umgehen. Und hier ergeben sich zwei Möglichkeiten:

• Wir verbinden den Anfang der vorherigen Iteration - den eindimensionalen Würfel mit dem Anfang seines Klons. Bis zur Symmetrie ist dies dasselbe wie das Verbinden des Endes mit dem Ende. Die Art der Symmetrie ist Spiegel. Diese Option wird bedingt als "Missionar" bezeichnet.
  
• Wir verbinden das Ende der vorherigen Iteration mit dem Beginn des Klons. Bis zur Symmetrie entspricht dies dem Verbinden des Zeilenanfangs mit dem Ende eines Klons. Die Art der Symmetrie ist zentral. Wir nennen diese Option einen "Zug".

Wir verhalten uns ähnlich bei dreidimensionalen oder mehrdimensionalen Fällen.


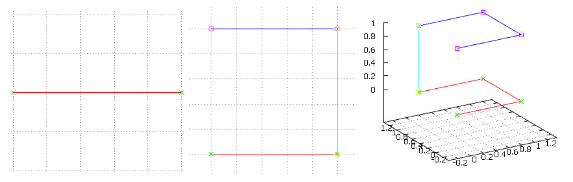Abbildung 3 Die ersten beiden Iterationen der Missionarsversion

Hier ist die vorherige Iteration rot hervorgehoben, ihr Klon ist blau und ihre Verbindung ist türkis.

Beachten Sie, dass die Verbindung immer eine einzige Dimension durchläuft - die neu hinzugefügte. Daher wird das Hauptmerkmal des Gray-Codes aufgrund der Selbstähnlichkeit angezeigt. Und da das Ende der vorherigen Iteration mit dem Ende des Klons verbunden ist, kommt es zu einer „Spiegelung“ - wenn wir herumgehen, müssen wir den Klon in umgekehrter Reihenfolge durchlaufen. Unabhängig von der Dimension. Hier können Sie den Ursprung und die Merkmale der Hilbert-Kurve sehen - egal wie groß das Gitter (in jeder Dimension) ist, auf der Basisebene ist es immer noch der gleiche Einheitswürfel mit Übergängen der Länge eins.


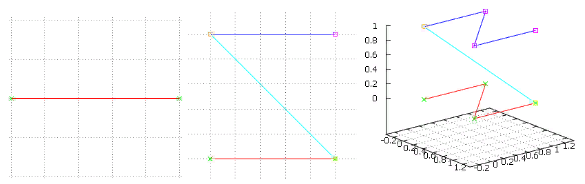Abbildung 4 Die ersten beiden Iterationen der Option „trainieren“ haben die gleichen Farben

Diese Musik ist uns aber auch vertraut - wir haben eine Simplex- Z-Kurve . Das Wort Simplex bedeutet hier auch, dass wir, wenn wir jeden seiner Punkte nehmen und durch einen Simplex ersetzen, einen 4x4x4-Würfel erhalten, der Iterationen fortsetzt - wir können ein beliebig großes kubisches Gitter füllen.

Es ist lustig, dass in diesem Fall die Konvertierung des vom Ursprung zum Code übergebenen Pfades, der in Bits zerlegt werden kann, trivial ist.
Während der Fall des Gray-Codes G = W ^ (W >> 1) ist, wobei W die übergebene Länge ist, ist G der Gray-Code.


Abbildung 5: Erste zwei Iterationen der Z-Kurve (Wiki)


6 zum Vergleich die ersten beiden Iterationen der Hilbert-Kurve (Wiki)

Es gibt jedoch keine anderen (natürlichen) Möglichkeiten, einen einzelnen Hyperwürfel zu umgehen.
So stellt sich heraus, dass wo immer Sie werfen, um Hilbert, Lebesgue ... und Leere .

PS : Im Titelbild ein kreisförmiger Encoder mit einem achtstelligen Gray-Code.
PPS : Hier korrigieren sie mich, dass der Begriff " Simplex" gut eingeführt ist und nicht gut damit umgehen kann. Nun, dieser Artikel ist nicht nur ein Simplex, sondern ein Simplex einer Hilbert-Kurve oder ein Simplex einer Z-Kurve. Mögen treue Mathematiker mir vergeben.