Visuelle Informationstheorie (Teil 2)

Der zweite Teil der Übersetzung des Longrid widmete sich der Visualisierung von Konzepten aus der Informationstheorie. Der zweite Teil befasst sich mit Entropie, Kreuzentropie, Kullback-Leibler-Divergenz, gegenseitiger Information und gebrochenen Bits. Alle Konzepte sind mit hervorragenden visuellen Erklärungen versehen.

Der Vollständigkeit halber empfehle ich Ihnen, sich vor dem Lesen des zweiten Teils mit dem ersten vertraut zu machen .

Entropieberechnung

Denken Sie daran, dass die Kosten einer Nachricht lang sind $$$L$ ist gleich $$$\ frac {1} {2 ^ L}$ . Wir können diesen Wert invertieren, um die Länge der Nachricht zu erhalten, die den angegebenen Wert hat: $$$\ log_2 (\ frac {1} {cost})$ . Da verbringen wir $$$p (x)$ pro Codewort für $$$x$ wird die Länge gleich sein $$$\ log_2 (\ frac {1} {p (x)})$ . In der Figur die Wahl der besten Längen von Codewörtern.



Wir haben zuvor diskutiert, dass es eine grundlegende Grenze dafür gibt, wie kurz eine durchschnittliche Nachricht sein kann, um Ereignisse aus einer bestimmten Wahrscheinlichkeitsverteilung zu übermitteln $$$p$ . Diese Grenze, die durchschnittliche Nachrichtenlänge bei Verwendung des besten Codierungssystems, wird als Entropie bezeichnet $$$p, H (p)$ . Jetzt, da wir die optimale Codewortlänge kennen, können wir sie berechnen!

$$

$$H (p) = \ sum_xp (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

(Oft wird Entropie geschrieben als $$$H (p) = - \ sum p (x) \ log_2 (p (x))$ unter Verwendung der Gleichheit $$$\ log (1 / a) = - \ log (a)$ . Die erste Version scheint mir intuitiver zu sein, daher werden wir sie weiter verwenden.)

Wenn ich berichten möchte, welches Ereignis passiert ist, muss ich im Durchschnitt so viele Bits senden, egal was ich tue.

Die durchschnittliche Menge an Informationen, die zum Übertragen von etwas benötigt wird, hat direkte Auswirkungen auf die Komprimierung. Aber gibt es noch andere Gründe, warum wir uns darum kümmern sollten? Ja Es beschreibt meine Unsicherheit und ermöglicht die Quantifizierung von Informationen.

Wenn ich sicher wäre, was passieren würde, müsste ich überhaupt keine Nachricht senden! Wenn es zwei Dinge gibt, die mit einer Wahrscheinlichkeit von 50% passieren können, muss ich nur 1 Bit senden. Aber wenn es 64 verschiedene Ereignisse gibt, die mit der gleichen Wahrscheinlichkeit auftreten können, muss ich 6 Bits senden. Je konzentrierter die Wahrscheinlichkeit ist, desto mehr Möglichkeiten habe ich, intelligenten Code mit kurzen Mediennachrichten zu erstellen. Je vager die Wahrscheinlichkeit, desto länger sollten meine Beiträge sein.

Je unsicherer das Ergebnis, desto mehr lerne ich im Durchschnitt, wenn sie mir erzählen, was passiert ist.

Kreuzentropie

Kurz vor seinem Umzug nach Australien heiratete Bob Alice, ebenfalls eingebildet. Zu meiner Überraschung und zur Überraschung anderer Charaktere in meinem Kopf war Alice keine Hundeliebhaberin. Sie war eine Katzenliebhaberin. Trotzdem konnten sie eine gemeinsame Sprache in ihrer allgemeinen Tierbesessenheit und ihrem sehr begrenzten Wortschatz finden.



Diese beiden verwenden die gleichen Wörter, nur mit unterschiedlichen Frequenzen. Bob spricht die ganze Zeit über Hunde, Alice spricht die ganze Zeit über Katzen.

Alice hat mir zuerst Nachrichten mit Bobs Code geschickt. Leider waren ihre Beiträge länger als erforderlich. Bobs Code wurde für seine Wahrscheinlichkeitsverteilung optimiert. Alice hat eine andere Wahrscheinlichkeitsverteilung und der Code ist nicht optimal für sie. Die durchschnittliche Codewortlänge, wenn Bob seinen Code verwendet, beträgt 1,75 Bit, wenn Alice ihn verwendet, dann 2,25. Es wäre noch schlimmer, wenn die beiden nicht so ähnlich wären!

Die durchschnittliche Nachrichtenlänge von einer Verteilung mit dem optimalen Code für eine andere Verteilung wird als Kreuzentropie bezeichnet. Formal können wir die Kreuzentropie wie folgt definieren:

$$

$$H_p (q) = \ sum_xq (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

In diesem Fall sprechen wir über die Kreuzentropie der Worthäufigkeit von Alices Katzenwurm in Bezug auf die Worthäufigkeit von Bobs Hundeliebhaber.



Um die Kosten für unsere Verbindung zu senken, bat ich Alice, ihren eigenen Code zu verwenden. Zu meiner Erleichterung verringerte sich dadurch die durchschnittliche Nachrichtenlänge. Dies führte jedoch zu einem neuen Problem: Manchmal verwendete Bob versehentlich Alices Code. Überraschenderweise ist es schlimmer, wenn Bob Alices Code verwendet als wenn Alice Bobs Code verwendet!

Nun haben wir also vier Möglichkeiten:

• Bob verwendet nativen Code ( $$$H (p) = 1,75$ bisschen)
• Alice benutzt Bobs Code ( $$$H_p (q) = 2,25$ bisschen)
• Alice benutzt ihren eigenen Code ( $$$H (q) = 1,75$ bisschen)
• Bob benutzt Alices Code ( $$$H_q (p) = 2,375$ bisschen)

Das ist nicht so intuitiv wie man denkt. Zum Beispiel können wir das sehen $$$H_p (q) ≠ H_q (p)$ . Können wir irgendwie sehen, wie diese vier Bedeutungen zueinander in Beziehung stehen?

In der folgenden Abbildung stellt jeder Untergraph eine dieser vier Möglichkeiten dar. Illustrationen veranschaulichen die durchschnittliche Länge einer Nachricht. Sie sind quadratisch angeordnet, sodass sich Diagramme in der Nähe befinden, wenn Nachrichten von derselben Verteilung stammen, und wenn sie dieselben Codes verwenden, liegen sie übereinander. Auf diese Weise können Sie Verteilungen und Codes visuell miteinander kombinieren.



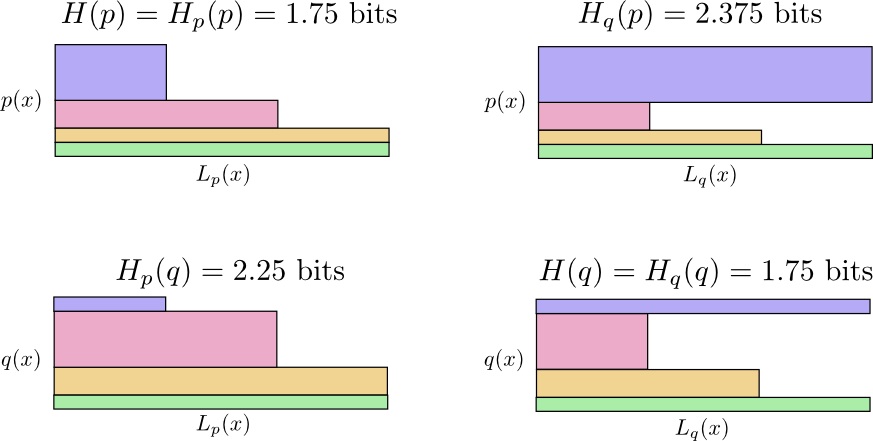
Sehen Sie warum $$$H_p (q) ≠ H_q (p)$ ? $$$H_q (p)$ so groß, weil das blau markierte Ereignis häufig auftritt, wenn $$$p$ bekommt aber ein langes codewort weil es für sehr selten ist $$$q$ . Andererseits häufige Ereignisse mit $$$q$ seltener mit $$$p$ Der Unterschied ist jedoch weniger dramatisch $$$H_p (q) Hp (q)$ ein bisschen weniger.

Die Kreuzentropie ist nicht symmetrisch.

Warum sollten Sie sich also für Kreuzentropie interessieren? Die Kreuzentropie gibt uns die Möglichkeit auszudrücken, wie unterschiedlich die beiden Wahrscheinlichkeitsverteilungen sind. Je unterschiedlicher die Verteilungen $$$p$ und $$$q$ die größere Kreuzentropie $$$p$ in Bezug auf $$$q$ es wird mehr Entropie geben $$$p$ .



Ebenso desto mehr $$$q$ verschieden von $$$p$ die größere Kreuzentropie $$$q$ in Bezug auf $$$p$ es wird mehr Entropie geben $$$q$ .

Das wirklich Interessante ist der Unterschied zwischen Entropie und Kreuzentropie. Dieser Unterschied entspricht der Länge unserer Posts, da wir Code verwendet haben, der für eine andere Distribution optimiert wurde. Wenn die Verteilungen gleich sind, ist diese Differenz Null. Mit zunehmenden Unterschieden wird es größer.

Wir nennen diesen Unterschied Kullback-Leibler-Divergenz oder einfach KL-Divergenz. KL Divergenz $$$p$ in Bezug auf $$$q$ , $$$D_q (p)$ wie folgt definiert:

$$

$$D_q (p) = H_q (p) - H (p)$$

Das Tolle an der KL-Divergenz ist, dass sie wie der Abstand zwischen zwei Verteilungen aussieht. Es misst, wie unterschiedlich sie sind! (Wenn Sie diese Idee ernst nehmen, kommen Sie zur Informationsgeometrie.)

Kreuzentropie und KL-Divergenz sind beim maschinellen Lernen unglaublich nützlich. Oft möchten wir, dass eine Distribution einer anderen nahe kommt. Beispielsweise möchten wir möglicherweise, dass die vorhergesagte Verteilung nahe an der zugrunde liegenden Wahrheit liegt. KL-Divergenz gibt uns einen natürlichen Weg, dies zu tun, und daher manifestiert sie sich überall.

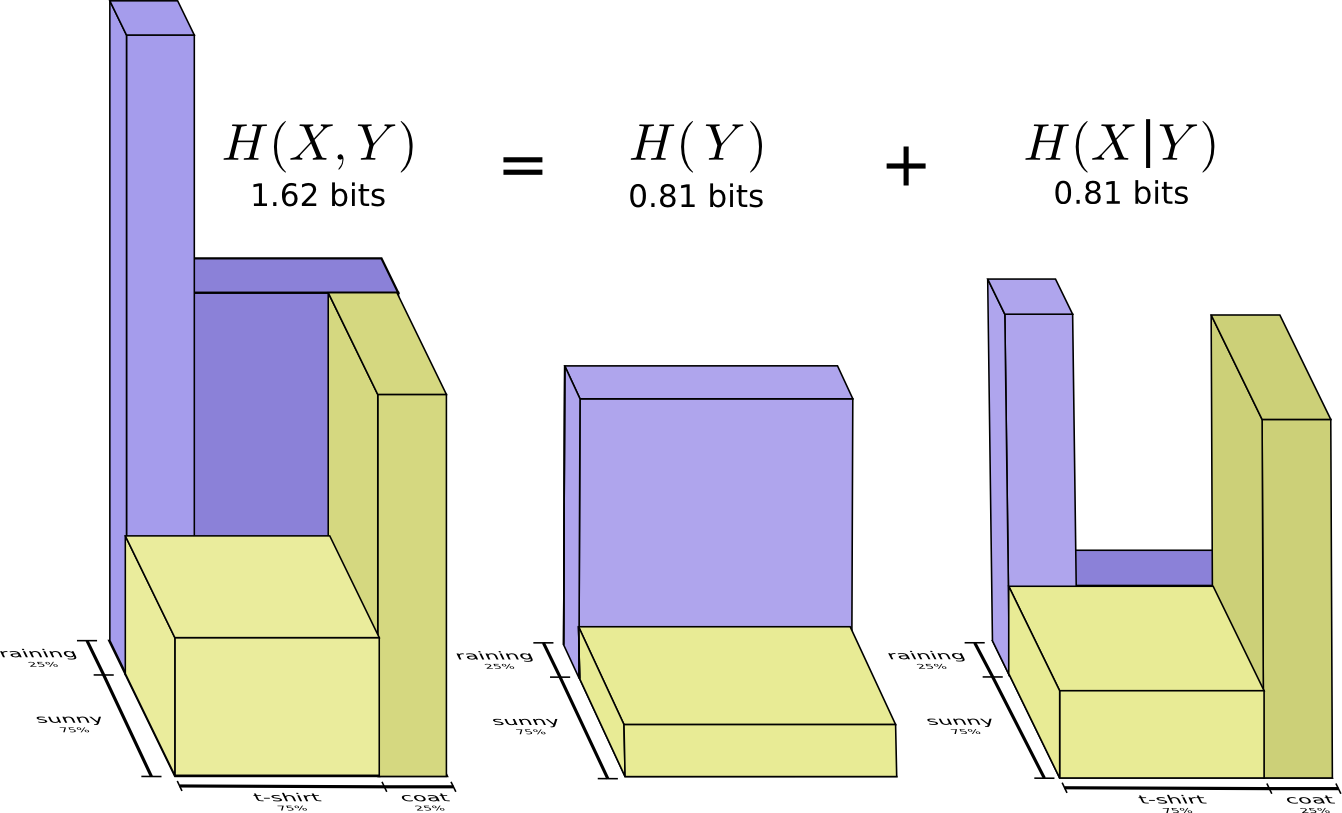
Entropie und mehrere Variablen

Kommen wir zu unserem Beispiel für Wetter und Kleidung zurück:




Meine Mutter macht sich wie viele Eltern manchmal Sorgen, dass ich mich dem Wetter nicht angemessen anziehe. (Sie hat guten Grund zur Vermutung - im Winter trage ich manchmal keinen Regenmantel.) Deshalb möchte sie oft wissen, wie das Wetter ist und was ich trage. Wie viele Bits sollte ich ihr schicken, um dies zu melden?

Der einfachste Weg, darüber nachzudenken, besteht darin, die Wahrscheinlichkeitsverteilung auszugleichen:



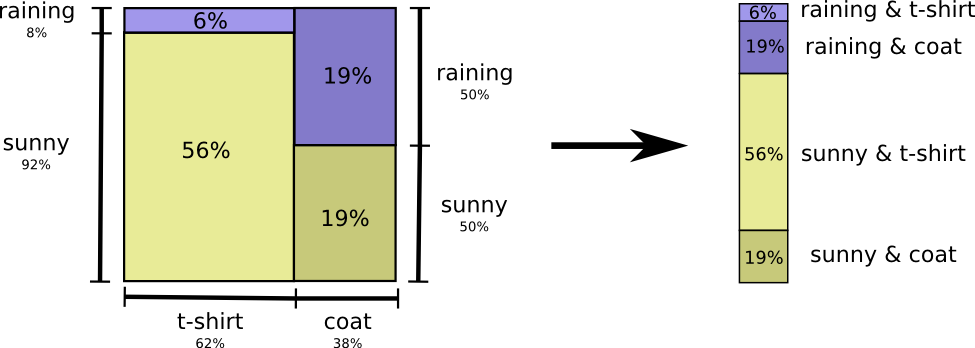
Jetzt können wir die optimalen Codewörter für Ereignisse mit solchen Wahrscheinlichkeiten berechnen und die durchschnittliche Nachrichtenlänge berechnen:



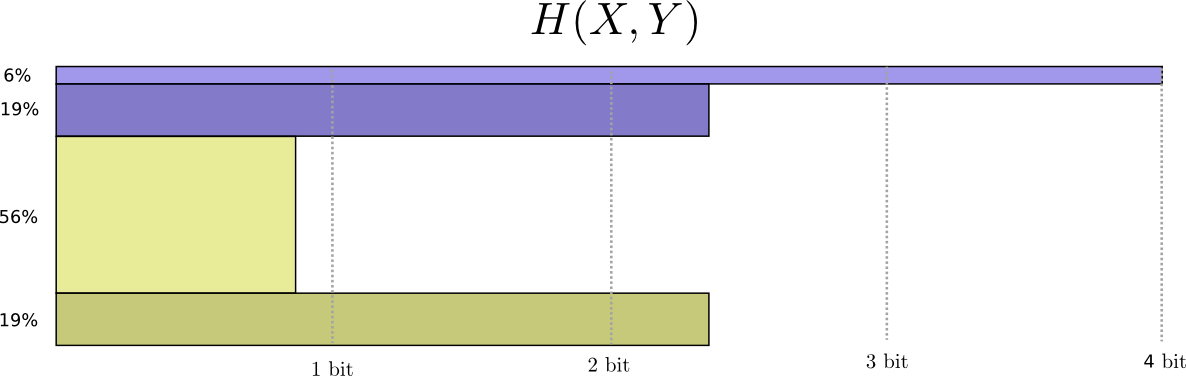
Wir nennen es gemeinsame Entropie $$$X$ und $$$Y$ wie folgt definiert:

$$

$$H (X, Y) = \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x, y)} \ bigg)$$

Es stimmt mit unserer üblichen Definition überein, mit Ausnahme von zwei Variablen anstelle von einer.

Ein etwas besseres Bild davon, ohne die Verteilung auszugleichen, wird erhalten, indem die Länge des Codeworts in der dritten Dimension dargestellt wird. Jetzt ist Entropie Volumen!



Angenommen, meine Mutter kennt das Wetter bereits. Sie kann sie in den Nachrichten sehen. Wie viele Informationen muss ich bereitstellen?

Anscheinend muss ich genügend Informationen senden, um zu erfahren, welche Kleidung ich trage. Tatsächlich muss ich jedoch weniger Informationen senden, da das Wetter, das ich trage, stark vom Wetter abhängt. Betrachten wir den Fall von Regen und Sonne getrennt.



In beiden Fällen muss ich im Durchschnitt nicht zu viele Informationen senden, da das Wetter mir eine gute Vorstellung davon gibt, wie die richtige Antwort aussehen wird. Wenn die Sonne scheint, kann ich einen speziellen Code verwenden, der für die Sonne optimiert ist, und wenn es regnet, kann ich den Code verwenden, der für Regen optimiert ist. In beiden Fällen sende ich weniger Informationen, als wenn ich gemeinsamen Code für beide verwendet hätte. Um die durchschnittliche Menge an Informationen zu erhalten, die ich meiner Mutter schicken muss, habe ich diese beiden Fälle einfach zusammengefasst ...



Wir nennen dies bedingte Entropie. Wenn Sie es in eine Gleichung formulieren, erhalten Sie:

$$

$$H (X | Y) = \ sum_yp (y) \ sum_xp (x | y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

$$

$$= \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

Gegenseitige Information

Im vorherigen Abschnitt haben wir herausgefunden, dass die Kenntnis einer Variablen dazu führen kann, dass weniger Informationen erforderlich sind, um den Wert einer anderen Variablen zu kommunizieren.

Eine gute Möglichkeit, darüber nachzudenken, besteht darin, sich die Informationsmenge in Form von Streifen vorzustellen. Diese Bänder überlappen sich, wenn sie gemeinsame Informationen enthalten. Zum Beispiel einige der Informationen in $$$X$ und $$$Y$ daher gemeinsam $$$H (X)$ und $$$H (Y)$ sind überlappende Streifen. Und seitdem $$$H (X, Y)$ Sind die Informationen beider Variablen, so ist dies die Vereinigung der Bänder $$$H (X)$ und $$$H (Y)$ .



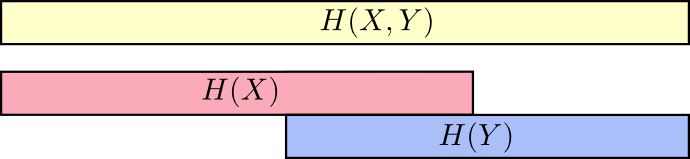
Wenn wir die Dinge so betrachten, wird vieles leichter zu sehen.

Beispielsweise haben wir bereits darauf hingewiesen, dass zur Übermittlung von Informationen als $$$X$ , so und $$$Y$ ("Gemeinsame Entropie", $$$H (X, Y)$ ) sind mehr Informationen erforderlich als nur für die Übermittlung $$$X$ ("Ultimative Entropie", $$$H (X)$ ) Aber wenn du es schon weißt $$$Y$ dann zur Übertragung $$$X$ ("Bedingte Entropie", $$$H (X | Y)$ ) Es werden weniger Informationen benötigt, als wenn Sie dies nicht wüssten!



Es klingt kompliziert, aber wenn man in Bands übersetzt, ist alles sehr einfach. $$$H (X | Y)$ Sind die Informationen, die wir senden müssen, um zu informieren $$$X$ einer, der es schon weiß $$$Y$ Informationen in $$$X$ das ist auch nicht in $$$Y$ . Optisch bedeutet dies, dass $$$H (X | Y)$ - Dies ist ein Teil des Streifens $$$H (X)$ die nicht überlappen mit $$$H (Y)$ .

Jetzt können Sie die Ungleichung lesen $$$H (X, Y) ≥H (X) ≥H (X | Y)$ gleich auf der nächsten Karte.



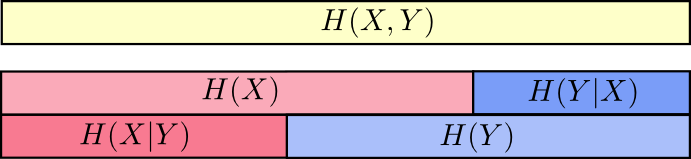
Eine andere Gleichheit ist wie folgt: $$$H (X, Y) = H (Y) + H (X | Y)$ . Das heißt Informationen in $$$X$ und $$$Y$ Das sind Informationen in $$$Y$ plus Informationen in $$$X$ das ist nicht in $$$Y$ .



Auch dies ist in den Gleichungen schwer zu erkennen, aber leicht zu erkennen, wenn man überlappende Informationsbereiche betrachtet.

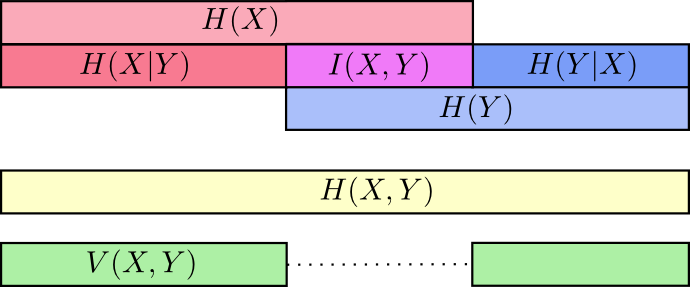
Zu diesem Zeitpunkt haben wir die Informationen in aufgeteilt $$$X$ und $$$Y$ in mehrfacher Hinsicht. Wir kennen die Informationen in jeder Variablen, $$$H (X)$ und $$$H (Y)$ . Wir kennen die Kombination von Informationen in beiden $$$H (X, Y)$ . Wir haben Informationen, die in einer Variablen sind, aber nicht in einer anderen, $$$H (X | Y)$ und $$$H (Y | X)$ . Ein Großteil davon dreht sich um Informationen, die Variablen gemeinsam sind - die Schnittmenge ihrer Informationen. Wir nennen es "gegenseitige Information" $$$I (x, y)$ definiert als:

$$

$$I (X, Y) = H (X) + H (Y) - H (X, Y)$$

Diese Definition ist wahr, weil $$$H (X) + H (Y)$ enthält zwei Kopien von gegenseitigen Informationen, da es sich auch in befindet $$$X$ und in $$$Y$ , während $$$H (X, Y)$ enthält nur eine Kopie. (siehe vorheriges Diagramm)

Die Variation von Informationen hängt eng mit der gegenseitigen Information zusammen. Variation von Informationen ist Information, die Variablen nicht gemeinsam ist. Wir können es so definieren:

$$

$$V (X, Y) = H (X, Y) - I (X, Y)$$

Die Variation von Informationen ist insofern interessant, als sie uns eine Metrik gibt, das Konzept des Abstands zwischen verschiedenen Variablen. Die Variation der Informationen zwischen zwei Variablen ist Null, wenn Sie den Wert einer Variablen kennen, der die Bedeutung der anderen Variablen angibt, und größer wird, wenn sie unabhängiger werden.

In welcher Beziehung steht dies zur KL-Divergenz, die uns auch das Konzept der Distanz gibt? KL-Divergenz ist der Abstand zwischen zwei Verteilungen über dieselbe Variable oder Variablenmenge. Im Gegenteil, Variation von Informationen gibt uns den Abstand zwischen zwei gemeinsam verteilten Variablen. KL-Divergenz ist eine Diskrepanz zwischen Verteilungen, eine Variation von Informationen innerhalb einer Verteilung.

Wir können alles in einem einzigen Diagramm zusammenfassen, das all diese verschiedenen Arten von Informationen miteinander verbindet:

Bruchbits

Eine sehr unintuitive Sache in der Informationstheorie ist, dass wir eine gebrochene Anzahl von Bits haben können. Das ist ziemlich komisch. Was bedeutet ein halbes bisschen?

Hier ist eine einfache Antwort: Oft interessiert uns eher die durchschnittliche Länge einer Nachricht als die Länge einer bestimmten Nachricht. Wenn in der Hälfte der Fälle ein Bit und in der Hälfte der Fälle zwei gesendet werden, werden durchschnittlich anderthalb Bits gesendet. Es ist nichts Seltsames an der Tatsache, dass Durchschnittswerte gebrochen sein können.

Aber mit dieser Antwort schrecken wir vor der Frage zurück. Oft sind die optimalen Codewortlängen auch gebrochen. Was bedeutet das?

Um genau zu sein, schauen wir uns die Wahrscheinlichkeitsverteilung an, bei der ein Ereignis, $$$a$ passiert 71% der Zeit, und ein anderes Ereignis, $$$b$ tritt 29% der Zeit auf.



Der optimale Code verwendet 0,5 Bit zur Darstellung $$$a$ und 1,7 Bits darzustellen $$$b$ . Nun, wenn wir nur eines dieser Codewörter senden wollen, ist eine solche Darstellung unmöglich. Wir sind gezwungen, auf eine ganzzahlige Anzahl von Bits zu runden und durchschnittlich 1 Bit zu senden.

... Aber wenn wir mehrere Nachrichten gleichzeitig senden, können wir es besser machen. Betrachten wir die Übertragung von zwei Ereignissen aus dieser Verteilung. Wenn wir sie unabhängig voneinander senden würden, müssten wir zwei Bits senden. Wie verbessern wir das?



In der Hälfte der Fälle müssen wir senden $$$aa$ in 21% der Fälle $$$ab$ oder $$$ba$ und in 8% der Fälle - $$$bb$ . Wiederum enthält ein idealer Code Bruchbits.



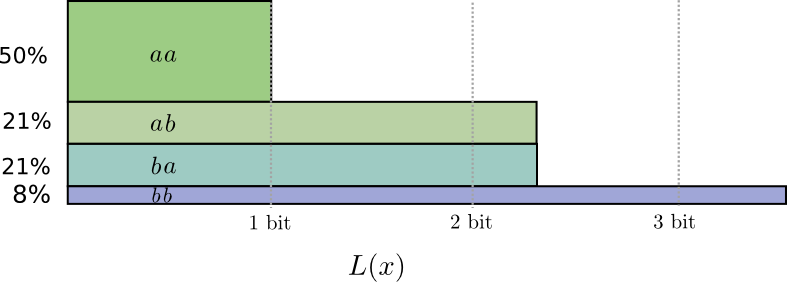
Wenn wir die Codewortlängen abrunden, erhalten wir etwa Folgendes:



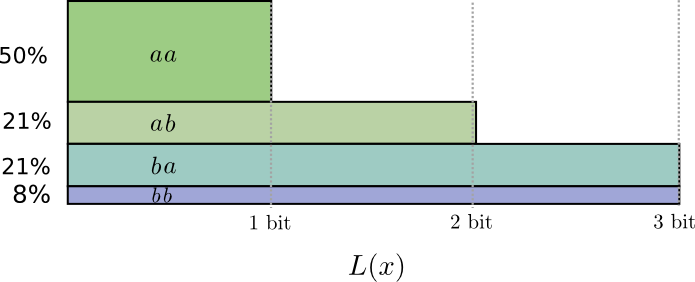
Diese Codes ergeben eine durchschnittliche Nachrichtenlänge von 1,8 Bit. Dies sind weniger als 2 Bits, wenn Nachrichten unabhängig gesendet werden. Das heißt In diesem Fall senden wir durchschnittlich 0,9 Bits für jedes Ereignis. Wenn wir mehr Ereignisse auf einmal senden würden, wäre der Durchschnitt noch geringer. Bei $$$n$ gegen unendlich tendierend, wird der mit dem Runden unseres Codes verbundene Overhead verschwinden, und die Anzahl der Bits pro Codewort wird zur Entropie konvergieren.

Als nächstes ist die ideale Codewortlänge für das Ereignis zu beachten $$$a$ war 0,5 Bit und die ideale Länge für das Codewort $$$aa$ - 1 Bit. Ideale Codewortlängen addieren sich, auch wenn sie gebrochen sind! Wenn wir also mehrere Ereignisse gleichzeitig melden, addieren sich die Längen.

Wie wir sehen können, gibt es eine echte Bedeutung für Bruchzahlen von Informationsbits, selbst wenn die tatsächlichen Codes nur Ganzzahlen verwenden können.

(In der Praxis verwenden die Benutzer bestimmte Codierungsschemata, die in verschiedenen Fällen wirksam sind. Der Huffman-Code, der eigentlich die Art von Code ist, die wir hier skizziert haben, behandelt gebrochene Bits nicht sehr elegant - Sie müssen die Zeichen wie oben beschrieben gruppieren oder verwenden komplexere Tricks, um der Entropiegrenze näher zu kommen. Die arithmetische Codierung unterscheidet sich geringfügig, sie verarbeitet Bruchbits elegant, um asymptotisch optimal zu sein.)

Fazit

Wenn wir uns Gedanken über die Übertragung von Informationen für die Mindestanzahl von Bits machen, sind diese Ideen natürlich von grundlegender Bedeutung. Wenn es uns um Datenkomprimierung geht, löst die Informationstheorie die Hauptprobleme und gibt uns grundlegend korrekte Abstraktionen. Aber was ist, wenn es uns egal ist - ist das nicht exotisch?

Ideen aus der Informationstheorie tauchen in vielen Zusammenhängen auf: maschinelles Lernen, Quantenphysik, Genetik, Thermodynamik und sogar Glücksspiel. Praktiker in diesen Bereichen interessieren sich nicht für Informationstheorie, weil sie Informationen komprimieren möchten. Sie kümmern sich darum, dass es eine unwiderstehliche Verbindung zu ihrem Gebiet hat. Quantenverschränkung kann durch Entropie beschrieben werden. Viele Ergebnisse in der statistischen Mechanik und Thermodynamik lassen sich durch die Annahme einer maximalen Entropie von Dingen erzielen, die Sie nicht kennen. Gewinne und Verluste von Spielern hängen direkt mit der KL-Divergenz zusammen, insbesondere mit iterierten Setups.

Die Informationstheorie taucht an all diesen Orten auf, weil sie konkrete, grundlegende Formalisierungen für viele Dinge bietet, die wir ausdrücken müssen. Es gibt uns Möglichkeiten, die Unsicherheit zu messen und auszudrücken, wie unterschiedlich die beiden Glaubenssätze sind und dass die Antwort auf eine Frage die andere besagt: Wie verteilt ist die Wahrscheinlichkeit, der Abstand zwischen den Wahrscheinlichkeitsverteilungen und wie abhängig sind die beiden Variablen. Gibt es alternative, ähnliche Ideen? Natürlich. Aber die Ideen aus der Informationstheorie sind rein, sie haben wirklich gute Eigenschaften und basieren auf Prinzipien. In einigen Fällen sind diese Ideen genau das, was Sie brauchen, und in anderen Fällen sind sie ein praktischer Vermittler in einer chaotischen Welt.

Maschinelles Lernen ist das, was ich am besten kenne. Lassen Sie uns eine Minute darüber sprechen. Ein sehr häufiger Aufgabentyp beim maschinellen Lernen ist die Klassifizierung. Angenommen, wir möchten ein Bild betrachten und vorhersagen, ob es sich um ein Bild eines Hundes oder einer Katze handelt. Unser Modell könnte etwa so lauten: „Es besteht eine Wahrscheinlichkeit von 80%, dass es sich um ein Bild eines Hundes handelt, und eine Wahrscheinlichkeit von 20%, dass es sich um eine Katze handelt.“ Angenommen, die richtige Antwort ist ein Hund - wie gut oder schlecht ist die Wahrscheinlichkeit, von der wir gesprochen haben Was ist ein Hund zu 80% und wie viel besser wären 85%?

Dies ist eine wichtige Frage, da wir eine Vorstellung davon brauchen, wie gut oder schlecht unser Modell ist, um es für den Erfolg zu optimieren. Was sollen wir optimieren? Die richtige Antwort hängt davon ab, wofür wir das Modell verwenden: Interessiert es uns nur, ob unsere Vermutung richtig war, oder wie sicher wir in der richtigen Antwort sind?Wie schlimm ist es, sich getrost zu irren? Darauf gibt es keine einzige richtige Antwort. Und oft ist es unmöglich, die richtige Antwort zu finden, da wir nicht genau wissen, wie das Modell verwendet wird, um zu formalisieren, was uns letztendlich begeistert. Es gibt Situationen, in denen Kreuzentropie genau das ist, was uns Sorgen macht, aber das ist nicht immer der Fall. Häufig wissen wir nicht genau, was uns Sorgen macht, und Cross-Entropy ist ein wirklich guter Proxy.

Informationen geben uns eine starke neue Basis, um über die Welt nachzudenken. Manchmal ist es ideal für eine bestimmte Aufgabe; in anderen fällen nicht ganz, aber trotzdem extrem nützlich. Dieser Aufsatz hat nur die Oberfläche der Informationstheorie zerkratzt - es gibt grundlegende Themen wie Fehlerkorrekturcodes, die wir überhaupt nicht angesprochen haben, aber ich hoffe, ich habe gezeigt, dass die Informationstheorie ein wunderbares Thema ist, das nicht einschüchtern sollte.