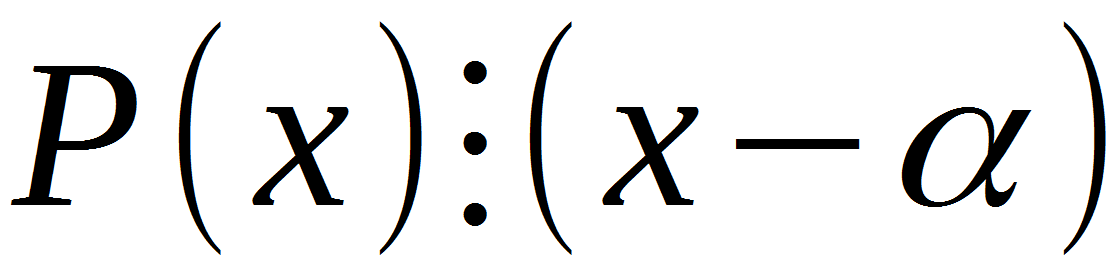
In der Regel werden wir in der Physik, der Informatik und der Wirtschaft mit den einfachsten linearen oder gebrochenen rationalen Gleichungen konfrontiert, seltener mit quadratischen. Und was ist mit Gleichungen dritten und vierten Grades? Wenn Sie interessiert sind, dann bitte ich um eine Katze.
Betrachten Sie zunächst das Konzept einer Gleichung höchsten Grades. Eine Gleichung höchsten Grades ist eine Gleichung der Form:

In diesem Artikel werde ich berücksichtigen:
1. Kubische Gleichungen.
2. Mehrweg kubisch.
3. Anwendung des Horner-Schemas und des Satzes von Bezout.
4. Mehrwegbiquadratische Gleichungen.
Kubische Gleichungen
Kubische Gleichungen sind Gleichungen, bei denen der Grad unbekannt für den Oberbegriff unbekannt ist. Kubische Gleichungen haben die folgende Form:

Solche Gleichungen können auf verschiedene Arten gelöst werden, wir werden jedoch das Wissen der Grundschule nutzen und die kubische Gleichung durch die Gruppierungsmethode lösen:

In diesem Beispiel wird die Gruppierungsmethode verwendet. Wir gruppieren die ersten beiden und die letzten beiden Elemente und erhalten dabei gleiche Klammern. Wir erkennen erneut die Gleichung von zwei Klammern.
Das Produkt ist dann gleich Null, und nur wenn mindestens einer der Faktoren gleich Null ist, setzen wir auf dieser Grundlage jeden Faktor (Klammer) gleich Null und erhalten eine unvollständige quadratische und lineare Gleichung.
Es ist auch anzumerken, dass die maximale Anzahl der Wurzeln einer Gleichung gleich dem Grad ist, der mit dem führenden Term unbekannt ist, so dass in einer kubischen Gleichung nicht mehr als drei Wurzeln, in einem biquadratischen (4. Grad) nicht mehr als vier Wurzeln und sein können. etc.
Kubische Gleichungen zurückgeben
Rückkehr kubische Gleichungen haben die Form:

Sie werden als Mehrweg bezeichnet, da die Koeffizienten gespiegelt werden. Ähnliche Gleichungen werden auch mit Schulmethoden gelöst, allerdings etwas kniffliger:

Zuerst wird eine Gruppierung durchgeführt, dann werden unter Verwendung der Formeln der abgekürzten Multiplikation die resultierenden Faktoren zerlegt. Wieder bekommen wir 2 gleiche Klammern, "wir nehmen sie raus". Wir erhalten zwei Faktoren (Klammern) und lösen sie als zwei verschiedene Gleichungen.
Bezouts Theorem und Horners Schema
Der Satz von Bezout wurde überraschenderweise von Etienne Bezout entdeckt, einem französischen Mathematiker, der sich hauptsächlich mit Algebra befasste. Der Satz von Bezout kann wie folgt formuliert werden:

Lass es uns herausfinden. P (x) ist ein beliebiges Polynom in x, (x - a) ist das Binom, in dem a eine der ganzzahligen Wurzeln der Gleichung ist, die wir unter den Teilern des freien Terms finden.
Drei Punkte, dies ist ein Operator, der angibt, dass ein Ausdruck durch einen anderen geteilt wird. Daraus folgt, dass wir, nachdem wir mindestens eine Wurzel einer gegebenen Gleichung gefunden haben, diesen Satz darauf anwenden können. Aber warum wird dieser Satz benötigt, wie wirkt er sich aus? Der Satz von Bezout ist ein universelles Werkzeug, wenn Sie den Grad eines Polynoms senken möchten. Zum Beispiel kann die kubische Gleichung mit ihrer Hilfe in ein Quadrat, ein Biquadrat, eine Würfelform usw. umgewandelt werden.
Aber es ist eine Sache zu verstehen, aber wie teilt man? Natürlich können Sie es in eine Spalte unterteilen, aber diese Methode steht nicht jedem zur Verfügung, und die Wahrscheinlichkeit, einen Fehler zu machen, ist sehr hoch. Deshalb gibt es einen anderen Weg, das ist Horners Schema. Ich werde ihre Arbeit mit einem Beispiel erklären. Angenommen,

Wir haben also ein Polynom erhalten, und wir haben vielleicht schon im Voraus eine der Wurzeln gefunden. Nun zeichnen wir eine kleine Platte mit 6 Spalten und 2 Zeilen, in jede Spalte der ersten Zeile (mit Ausnahme der ersten) geben wir die Koeffizienten der Gleichung ein. Und in der ersten Spalte von Zeile 2 addieren wir den Wert von a (die gefundene Wurzel). Dann den ersten Koeffizienten, in unserem Fall 5, sprengen wir einfach. Die Werte der folgenden Spalten werden wie folgt berechnet:

(Das Bild ist
hier ausgeliehen )
Als nächstes machen wir dasselbe mit dem Rest der Spalten. Der Wert der letzten Spalte (2 Zeilen) ist der Rest der Division, in unserem Fall 0. Wenn Sie eine andere Zahl als 0 erhalten, müssen Sie einen anderen Ansatz wählen. Ein Beispiel für eine kubische Gleichung:

Mehrwegbiquadratische Gleichungen
Wir haben oben auch kubische Rückkehrgleichungen betrachtet und jetzt analysieren wir biquadratische Gleichungen. Ihre allgemeine Ansicht:

Anders als bei der kubischen Rückkehrgleichung hat nicht jeder ein biquadratisches Paar in Bezug auf die Koeffizienten, aber ansonsten sind sie sehr ähnlich. Hier ist der Algorithmus zum Lösen solcher Gleichungen:

Wie Sie sehen, ist das Lösen solcher Gleichungen keineswegs einfach. Aber ich werde diesen Fall trotzdem ausmachen. Die Lösung beginnt mit der Division der gesamten Gleichung durch x ^ 2. Als nächstes gruppieren wir, hier habe ich aus Gründen der Klarheit eine zusätzliche Zeile eingeführt. Danach machen wir den Trick und setzen die erste Klammer 2 ein, die wir zuerst addieren und dann subtrahieren. Der Betrag wird sich trotzdem nicht ändern, aber jetzt können wir diese Klammer in das Quadrat der Summe falten.
Wir entfernen -2 aus der Klammer und multiplizieren es zuerst mit a. Danach führen wir eine neue Variable t ein und erhalten die quadratische Gleichung.
Kommen wir nun zu einem Beispiel:

Der Hauptteil wird, wie im verallgemeinerten Algorithmus, durch x ^ 2 geteilt, gruppiert, zu einem vollen Quadrat zusammengefasst, wir führen eine variable Substitution durch und lösen die quadratische Gleichung. Danach setzen wir die erhaltenen Wurzeln zurück und lösen 2 weitere quadratische Gleichungen (multipliziert mit x).
Anwendungsgebiet
Aufgrund ihres Umfangs und ihrer Spezifität finden Gleichungen höheren Grades selten Anwendung. Es gibt jedoch noch Beispiele, die Poisson-Gleichung für adiabatische Prozesse in der Physik.
Fazit
In diesem Artikel habe ich nur kubische und biquadratische Gleichungen betrachtet. Das in Betracht gezogene Bezout-Theorem (und das Horner-Schema) können jedoch zur Lösung von Gleichungen mit 5, 6, 7 und anderen Graden verwendet werden, auch wenn ihre Anwendung begrenzt ist.