GPR-Modellierung

Georadar (Funktechnisches Gerät für Untergrundsonden, GPR, Ground Penetrating Radar), das derzeit sehr häufig eingesetzt wird - von der Kartierung von Kaninchenlöchern und dem Studium von Eidechsen bis zur Suche nach Minen - ist nach wie vor ein ziemlich teures Vergnügen.


GPR-Display (Frame aus der britischen TV-Show "Command of the Time")

Es ist jedoch möglich, seine Fähigkeiten zu bewerten und verschiedene Aspekte der Wechselwirkung des elektromagnetischen Feldes des Georadars mit der Umwelt zu untersuchen, ohne ein „Eisen“ -Gerät zu erwerben oder zu mieten. Das unter der GNU GPL v3-Lizenz vertriebene gprMax- Paket ( gpr - aus der GPR-Abkürzung, Max - die Anfangsbuchstaben des Namens von James Clerk Maxwell, der die Grundlagen der Elektrodynamik legte) wird uns dabei helfen.
Die Autoren dieses 1996 begonnenen Projekts sind Craig Warren von der University of Northumbria und Antonis Giannopoulos von der University of Edinburgh. Das Paket wurde ursprünglich in C entwickelt und dann in Python 3 / Cython-Kombinationen vollständig neu geschrieben.


Für die Installation des Pakets sind installierte Compiler erforderlich, die OpenMP (Microsoft Visual C ++ 2015 Build Tools (diese Version wird empfohlen!) Für Windows / gcc für Linux), die NumPy-Bibliothek und den Cython-Compiler unterstützen. Wechseln Sie nach dem Herunterladen aus dem Repository auf GitHub und dem Entpacken des Quellcodes des Projekts in den Stammordner und führen Sie die folgenden Befehle aus:

python setup.py build python setup.py install 

Als „Schnellstart“ betrachten wir die Arbeit mit dem Paket anhand eines einfachen zweidimensionalen Beispiels: Die Sendeantenne T eines gepulsten Radars (Impuls GPR) sendet einen elektromagnetischen Impuls aus, von dem ein Teil der Energie direkt die Empfangsantenne R in Form einer direkten Welle (DW - direct wave) erreicht und teilweise durchdringt Durch den Sand wird es von der Oberfläche des leitenden Zylinders reflektiert und erreicht die Empfangsantenne in Form einer reflektierten Welle (RW - Reflected Wave):


Eingabedateiformat
Erstellen Sie den Ordner models im Stammverzeichnis des Projekts, in dem die Textdatei hello.in mit den Befehlen zur Durchführung der Simulation abgelegt ist (die folgenden Befehle entsprechen der aktuellen (dritten) Version des Projekts).

Jedes Team hat die Form:

 #: _1 _2 _3 ... 

In eine Zeile kann nur ein Befehl geschrieben werden, und das erste Zeichen der Zeile, die den Befehl enthält, muss # sein.

Befehle können mit Kommentaren versehen werden:

 ## 

Die Reihenfolge der Befehle ist wichtig für die Befehle zum Erstellen von Objekten. Diese Befehle werden in der Reihenfolge ausgeführt, in der sie in der Eingabedatei angezeigt werden.

Pulsform

Ein von einem Georadar ausgesandter elektromagnetischer Impuls dauert einige Bruchteile einer Nanosekunde. Außerdem werden am häufigsten drei Impulsformen verwendet:

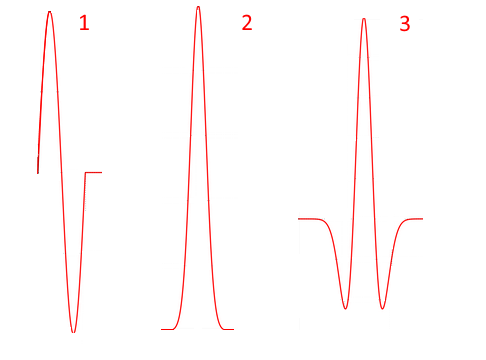
1. eine Sinuswellenperiode (Sinus)
2. Gaußscher Impuls
3. Der mexikanische Hut (Ricker) ist proportional zur zweiten Ableitung der Gaußschen Funktion, die Kurvenform eines solchen Impulses ähnelt einem Sombrero (diese Impulsform wurde vom amerikanischen Geophysiker Norman Ricker 1953 zur Untersuchung seismischer Signale verwendet).
   

In unserem Beispiel wählen wir einen Gauß-Impuls (Impulstyp - Gauß) mit einer Mittenfrequenz $$$f_c = 1 \\ GHz = 1 \ cdot 10 ^ 9 Hz$ definiert durch den Befehl:

 #waveform: gaussian 1 1e9 pulse 

(1 - bedingte Pulsamplitude, Puls - Pulsbezeichnung)

In diesem Fall wird der in der Simulation verwendete Impuls durch den folgenden Ausdruck beschrieben:

$$

$$W (t) = e ^ {- 2 \ cdot {\ pi} ^ 2 \ cdot {f_c} ^ 2 {(t- {1 \ over {f_c}}) ^ 2}$$

Umgebungsmodell und Koordinatensystem

Bei der 2D - Modellierung wird der untersuchte Bereich in Zellen einer bestimmten Größe unterteilt, und das Modellkoordinatensystem sieht folgendermaßen aus: Die X - und Y - Achsen bilden eine berechnete Ebene (mit einer Breite) $$$w$ und groß $$$h$ ) hat die Länge des Modells entlang der Z-Achse einen Wert, der dem Abtastschritt entspricht $$$\ Delta$ .


Bei der Auswahl eines Abtastschritts können Sie der Faustregel folgen: Die Schrittgröße sollte ein Zehntel der kleinsten im Modell untersuchten Wellenlänge („10 Zellen pro Wellenlänge“) nicht überschreiten:

$$

$$\ Delta \ le 0,1 \ cdot {\ lambda} _ {min}$$

Um die Wellenlänge zu bestimmen, muss man die maximale Frequenz kennen, die in dem Spektrum des ausgesandten Signals und der Wellengeschwindigkeit in dem betrachteten Medium berücksichtigt wird.

Die Ausbreitungsgeschwindigkeit einer elektromagnetischen Welle in einem Medium mit relativer Dielektrizitätskonstante $$${\ epsilon} _r$ ausgedrückt in Zentimetern pro Nanosekunde - die Geschwindigkeitseinheit, die im Radar angenommen wird, wird durch den Ausdruck bestimmt:

$$

$$v = {30 \ over {\ sqrt {{\ epsilon} _r}}}$$

Die Wellenlänge in Zentimetern wird durch den Ausdruck bestimmt:

$$

$$\ lambda = {v \ over f}$$

( $$$f$ - Frequenz in GHz).
Mit dem folgenden Befehl können Sie die Form des Gaußschen Impulses und sein Spektrum anzeigen:

 python -m tools.plot_source_wave gaussian 1 1e9 5e-9 1e-12 -fft 

(Gauß - Impulstyp, 1 - Impulsamplitude, 1e9 - Mittenfrequenz (1 GHz), 5e-9 - Impulsanzeigedauer (5 ns), 1e-12 - Zeitschritt (1 ps))


Nach dem Spektrum eines Gaußschen Impulses mit $$$f_s = 1 \ GHz$ Bestimmen Sie, dass bei -40 dB die Frequenz $$$f \ ca. 3 \ GHz$ .
In diesem Beispiel, dem Medium, in dem sich das untersuchte Objekt befindet, wird trockener Sand mit einer relativen Permittivität ausgewählt $$${\ epsilon} _r = 3$ .
Ermitteln Sie die Ausbreitungsgeschwindigkeit der elektromagnetischen Welle im Sand:

$$

$$v = {30 \ over {\ sqrt {3}}} = 17,3 \ cm / ns$$

Definieren Sie die Wellenlänge im Sand:

$$

$$\ lambda = {v \ over f} = {17,3 \ over {3}} = 5,8 cm = 58 mm$$

Darauf aufbauend wählen wir den für alle Achsen gleichen Schritt aus ( $$$\ Delta = {\ Delta} _x = {\ Delta} _y = {\ Delta} _z$ ) und aus praktischen Gründen gleich 2 mm = 0,002 m (eine ganzzahlige Anzahl von Schritten passt in 1 cm):

 #dx_dy_dz: 0.002 0.002 0.002 

Begrenzen Sie den simulierten Bereich auf ein Rechteck mit einer Breite $$$w$ gleich 80 cm = 0,8 m und höhe $$$h$ gleich 60 cm = 0,6 m:

 #domain: 0.60 0.60 0.002 

(Für ein zweidimensionales Modell muss eine Dicke angegeben werden, die einer Stufe entspricht (0,002).)

Die Größe des Simulationsbereichs und die räumliche Schrittgröße bestimmen die Anzahl der Modellzellen und dementsprechend den Speicherbedarf des Computers.

Wir beschreiben den Sand mit spezifischer Leitfähigkeit $$$\ sigma = 0,01 \ \ cm / m$ und relative Dielektrizitätskonstante $$${\ epsilon} _r = 3$ befehl:

 #material: 3 0.01 1 0 sand 

(1 entspricht der relativen magnetischen Permeabilität $$${\ mu} _r$ gleich eins (keine magnetischen Eigenschaften), 0 - kein magnetischer Verlust, und Sandetikett dieses Materials).

Füllen Sie den Sand mit dem größten Teil der simulierten Fläche (von y = 0 bis y = 38 cm = 0,38 m):

 #box: 0 0 0 0.80 0.38 0.002 sand 

(0 0 0 - Koordinaten der unteren linken Ecke, 0,80 0,38 0,002 - Koordinaten der oberen rechten Ecke (0,002 - Abtastschritt))
Der Rest ist freier Raum (Bezeichnung free_space), der in den Lufteigenschaften fast gleichwertig ist ( $$${\ epsilon} _r = 1$ , $$${\ mu} _r = 1$ , $$${\ sigma} = 0$ )
Die Grenzen des Simulationsbereichs werden als Absorbing Boundary Condition (ABC) dargestellt.

Als Ziel wählen wir einen Zylinder aus einem idealen Leiter (der elektromagnetische Strahlung vollständig reflektiert) mit einem Radius von 6 cm = 0,06 m und einem Mittelpunkt an einem Punkt mit den Koordinaten x = 25 cm = 0,25 m und y = 10 cm = 0,1 m:

 #cylinder: 0.250 0.1 0 0.250 0.1 0.002 0.06 pec 

(Pec ist ein perfekt leitfähiges Material)

Antennen

Der simulierte GPR ist mit zwei Antennen ausgestattet - Senden und Empfangen.
In unserer Fallstudie stellen wir eine Sendeantenne mit einem Hertz-Dipol dar, dessen Länge dem Abtastschritt entspricht (im dreidimensionalen Fall können Sie eine Antenne aus einer umfangreichen Bibliothek auswählen), die im Sand (in Kontakt mit dem untersuchten Medium) in einem Abstand von 5 cm links von der Mitte des Bereichs liegt (x = 35) cm = 0,35 m, y = 38 cm = 0,38 m):

 #hertzian_dipole: z 0.35 0.380 0.0 pulse 

(z ist die Dipolpolarisationsachse (für den zweidimensionalen Fall (2D-TMz-Modus) ist nur z gültig), Puls ist die Bezeichnung für die Form des von der Antenne ausgestrahlten Pulses.)

Die Empfangsantenne befindet sich normalerweise in einem geringen konstanten Abstand von der Empfangsantenne, die als Basis der Antenneneinheit bezeichnet wird (diese Option für die relative Position der Antennen wird als "gemeinsamer Versatz" bezeichnet). Wählen Sie als Basis einen Abstand von 10 cm, sodass die horizontale Koordinate 35 + 10 = 45 cm = 0,45 m beträgt (5 cm rechts von der Mitte des Bereichs):

 #rx: 0.45 0.38 0.0 

Simulationsintervall

Die Wahl des Zeitfensters für die Modellierung wird so festgelegt, dass das vom Ziel reflektierte Signal Zeit hat, die Empfangsantenne zu erreichen.

Wir bestimmen die ungefähre Zeit, die das Signal im betrachteten Fall benötigt, unter Berücksichtigung der Entfernung von den Antennen zum Ziel $$$h = 18 \ \ cm$ :
$$$t \ ungefähr {2 \ cdot h \ über {v}} = {2 \ cdot 18 \ über 17,3} = 2,1 \ \ ns$
Da die Spitze des Gaußschen Pulses des Radars mit einer Mittenfrequenz von 1 GHz relativ zum Beginn der Zeitachse um 1 ns verschoben ist, wählen wir ein Zeitfenster von 5 Nanosekunden:

 #time_window: 5e-9 

Modellierung

Der Inhalt der Eingabedatei lautet also wie folgt:


Wir starten den Modellierungsprozess:

 python -m gprMax models\hello.in 

Zur Durchführung der Simulation wird die Finite-Differenz-Zeitdomänen-Methode (FDTD, Finite-Differenz-Zeitdomäne) verwendet (der grundlegende Algorithmus der Methode wurde von Kane Yee vorgeschlagen), wonach die Zellen, in die das Modell unterteilt ist, als Yee-Zellen bezeichnet werden . Eine numerische Lösung wird im Zeitbereich erhalten, indem die Maxwell-Gleichungen für jede Zelle gelöst werden.

Im zweidimensionalen Fall (2D-TMz-Modus) wird nur die Komponente berechnet $$$E_z$ elektrisches Feld und Komponenten $$$H_x$ und $$$H_y$ magnetisches Feld.

Wenn der verfügbare Speicherplatz überschritten wird, wird eine Meldung über den Speichermangel ausgegeben, um die Simulation durchzuführen:


Wenn eines der Objekte außerhalb des Simulationsbereichs liegt, wird eine Fehlermeldung angezeigt:


Für die Simulation mit dem beschriebenen Modell wurden nur ca. 56 MB RAM benötigt (wenn Sie den Schritt um die Hälfte verringern - bis zu 1 mm -, steigt der Speicherbedarf auf 99 MB).

Nach Abschluss der Simulation wird die Datei " hello.out " im Ordner " models " angezeigt. Sie enthält die Simulationsergebnisse im HDF5-Format , das speziell zum Speichern von numerischen Daten entwickelt wurde.

Gleisbau

Um die Ergebnisse zu visualisieren, konstruieren wir die Traces:

 python -m tools.plot_Ascan models\hello.out 

Jede Spur (A-Scan), die in dem sich öffnenden Fenster angezeigt wird, zeigt ein Zeitdiagramm einer der Komponenten des elektromagnetischen Felds am Ort der Empfangsantenne:


Auf den Pfaden sind eine direkt von der Sendeantenne (DW) kommende Welle und eine vom Ziel (RW) reflektierte Welle sichtbar.

Die horizontale Zeitachse bezieht sich auf die Tiefe des Ziels, die das Signal durch die Geschwindigkeit der elektromagnetischen Welle in der Substanz reflektiert.

Aber was passiert, wenn Sie den Zylinder-Befehl in der Eingabedatei vor den Box-Befehl setzen?


Das vom Zylinder reflektierte Signal verschwand - der Sand absorbierte den Zylinder (dies ist ein Beispiel für die Bedeutung der Reihenfolge, in der die Objekte konstruiert werden).

Profilerstellung

Aber informativer ist das Radarogramm (Radargramm) - Profil (B-Scan), das eine Kombination aus vielen Spuren darstellt, die beim Bewegen des Georadars in eine bestimmte Richtung erstellt werden. Dies ist genau das Verfahren zum Bewegen eines Wagens mit einem Radar entlang des untersuchten Bereichs.

Ändern Sie die Beschreibung der Antennen, indem Sie sie an den Anfang der horizontalen Achse verschieben:

 #hertzian_dipole: z 0.10 0.38 0.0 pulse #rx: 0.20 0.38 0.0 

Wir setzen den Schritt zum Bewegen der Antennen auf 1 cm = 0,01 m:

 #src_steps: 0.01 0 0 #rx_steps: 0.01 0 0 

Der Inhalt der Eingabedatei lautet also wie folgt:


Führen Sie die Simulation im Batch-Modus aus:

 python -m gprMax models\hello.in -n 50 

(50 ist die Anzahl der Schritte, die das Radar bewegt).

Nach dem Start wird die Simulation nacheinander für 50 GPR-Positionen durchgeführt:


Nach dem Ende der Simulation befinden sich 50 Dateien hello1.out ... hello50.out im Modellordner.
Kombinieren Sie diese Dateien mit dem folgenden Befehl in die Datei hello_merged.out:

 python -m tools.outputfiles_merge models/hello 

Erstellen Sie ein Profil:

 python -m tools.plot_Bscan models\hello_merged.out Ez 

(Ez ist die Komponente des elektromagnetischen Feldes, mit dem wir das Profil erstellen - die Komponente, die direkt in Spannung umgewandelt wird)


Wie Sie sehen können, wird der horizontale Balken, der durch die direkte Welle verursacht wird, im Profil oben angezeigt, und die charakteristische Hyperbel, die durch die reflektierte Welle verursacht wird und die Änderung der Entfernung vom Ziel zum GPR zeigt, wenn es sich bewegt, wird unten angezeigt.

Die Legende rechts zeigt die passenden Farben und Feldstärken. $$$E_z$ (auf der Strecke gezeigt):
rot - $$$E_z> 0$
weiß - $$$E_z = 0$
blau - $$$E_z <0$
Durch die Analyse solcher Profile können Rückschlüsse auf die Tiefe, Größe und sogar die Form der Ziele gezogen werden, wobei auch neuronale Netze verwendet werden.


Routen und Profil auf dem GPR-Display (Frame aus der britischen Fernsehsendung "Command of the Time")

Reflexion tritt aber nicht nur an leitenden Objekten auf, sondern auch an der Grenze zweier Schichten mit unterschiedlichen Dielektrizitätskonstanten.

Erstellen Sie im unteren Teil des Modells eine zweite Sandschicht mit Dielektrizitätskonstante $$${\ epsilon} _r = 9$ :



Wie zu sehen ist, erschien unterhalb der "Spur" der direkten Welle (DW) ein lineares Segment der Welle (RW), das von der Grenzfläche der beiden Sandschichten reflektiert wurde.

Außerhalb dieses Beispiels können mit gprMax- Funktionen wie dreidimensionale Modellierung, komplexe Oberflächenformen, detaillierte Antennenmodelle, die Streuung elektromagnetischer Wellen usw. nicht nur die GPR simuliert, sondern auch die Ausbreitung elektromagnetischer Wellen in verschiedenen Umgebungen untersucht werden Beschleunigen Sie Berechnungen mit der NVIDIA CUDA- Technologie, die eine zehnfache Geschwindigkeitssteigerung im Vergleich zu Parallel-Computing auf einer CPU mit OpenMP bietet. Um die Flexibilität der Modellierung zu erhöhen, können Sie Codeblöcke in Python in die Eingabedatei einfügen.

Einige Beispiele für die Verwendung des gprMax-Pakets:

• Einschätzung der Auswirkung von Bodeneigenschaften auf die Wirksamkeit von GPR bei der Suche nach Antipersonenminen
• Prüfung der Möglichkeit der Verwendung von Bodenradar zur zerstörungsfreien Bestimmung der Pflanztiefe von Maissamen
• Verbesserung der Qualität der Interpretation von GPR-Felddaten bei der Untersuchung der Festigkeit von Strukturen von unterirdischen Durchgängen durch die Autobahn
• Untersuchung der Beziehung zwischen der Amplitude des reflektierten Signals und dem Durchmesser der Bewehrungsstäbe in Beton
• Einschätzung der Eignung von GPR zur Erkennung von Hohlräumen in Baumstämmen

Nützliche Links:

Offizielle Website von gprMax
GprMax Benutzerhandbuch
gprMax auf YouTube