Überall in der Geographie: Navigation und geodätische Aufgaben in verschiedenen Sprachen

Grüße, meine Lieben!

"... der wahre Ort des Schiffes ist zwar unbekannt, aber nicht zufällig, aber zu welchem ​​Zeitpunkt ist es unbekannt." V. Aleksishin et al. Practical Navigation, 2006. S. 71

"Fußgänger kamen aus den beiden Rändern der Galaxis ..." (C) Sergey Popov (Astrophysiker)

Angesichts der neuen Trends im Jugendstil wollte ich über das Lösen geodätischer Probleme auf ebenem Boden schreiben. Aber bis jetzt lade ich alle Interessierten ein, sich den konservativeren Modellen anzuschließen, die Aussage, dass die Form der Erde bequemerweise durch ein Ellipsoid angenähert wird, nicht als Ketzerei und Aufruhr zu betrachten.

• Entfernung zwischen zwei geografischen Punkten
• Bestimmung eines Punktes anhand der bekannten Entfernung und des Azimutwinkels
• Bestimmung der Position eines Punktes durch gemessene Entfernungen zu bekannten Punkten (TOA, TOF)
• Bestimmung der Position eines Punktes durch gemessene Signalankunftszeiten (TDOA)

All dies in C #, Rust und Matlab, auf der Kugel und den Ellipsoiden, mit Bildern, Grafiken, Quellcode - unter dem Schnitt.

Und das ist der relevante KDPV:



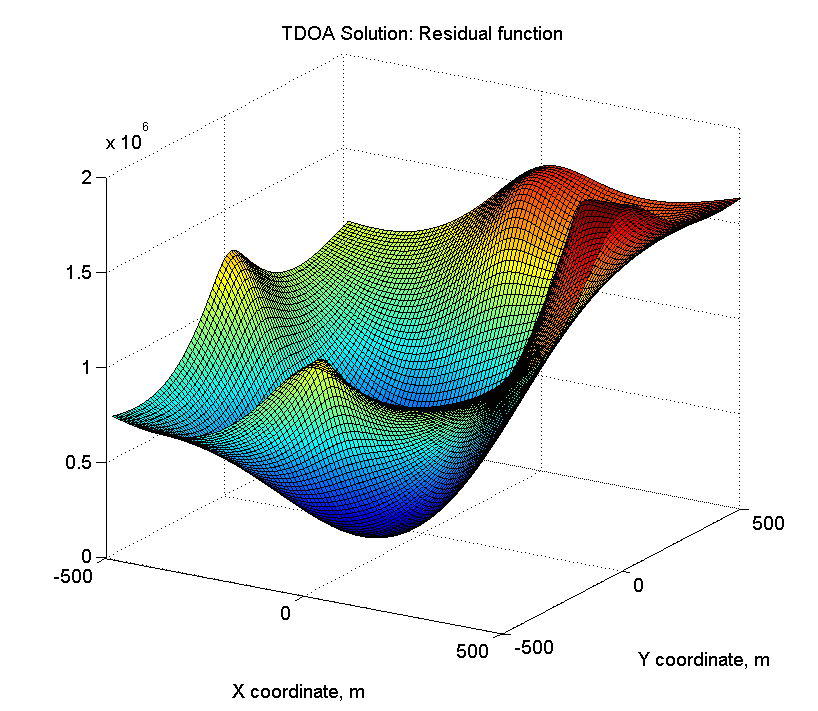
Für diejenigen, die es eilig haben (ich selbst bin es), ist hier das Repository auf GitHub , wo sich alle Quellcodes mit Tests und Beispielen befinden.

Das Repository ist sehr einfach organisiert: Die Bibliothek wird derzeit in drei Sprachen dargestellt und jede Implementierung befindet sich in einem eigenen Ordner:

• C #
• Rust
• Matlab

Die vollständigste Implementierung in C #: Im Gegensatz zu den anderen gibt es sogenannte Methoden Virtuelle lange Basis - Dies ist der Fall, wenn ein Objekt, dessen Position Sie bestimmen müssen, stationär ist und zu dem Abstände von verschiedenen Punkten mit einer bekannten Position gemessen werden.

Um zu sehen, wie alles funktioniert, mit welchen Parametern es aufgerufen wird und was zurückkehrt, und um im Kampf Aufklärung zu betreiben, gibt es verschiedene Demos und Tests:

• Konsolenanwendung in C # testen
• Testen Sie die gesamte Bibliothek auf Matlab
• TOA / TDOA-Demo- Skript mit schönen Bildern auf Matlab
• Skript auf Matlab zum Vergleichen der Genauigkeit von Lösungen für geodätische Probleme auf einer Kugel (Haversine-Gleichungen) und auf einem Ellipsoid (Vincenty-Gleichungen)
• Für die Implementierung auf Rust enthält der Bibliothekscode Tests. Und Sie können sehen, wie alles funktioniert, indem Sie einfach den Befehl „Cargo-Test“ ausführen

Ich habe versucht, die Bibliothek so unabhängig und autark wie möglich zu machen. Wenn Sie möchten, können Sie einfach das gewünschte Stück nehmen (natürlich unter Bezugnahme auf die Quelle), ohne alles andere zu ziehen.

Fast immer sind die Winkel im Bogenmaß, die Entfernungen in Metern und die Zeit in Sekunden.

Beginnen wir nun von vorne:

Vermessungsaufgaben

Es gibt zwei typische geodätische Aufgaben: direkt und invers.

Wenn ich zum Beispiel meine aktuellen Koordinaten (Breite und Länge) kenne und dann 1000 Kilometer genau nach Nordosten, gut oder Norden gelaufen bin. Welche Koordinaten habe ich jetzt? - Um herauszufinden, welche Koordinaten ich haben werde, muss man ein direktes geodätisches Problem lösen.

Das heißt: Eine direkte geodätische Aufgabe besteht darin, die Koordinaten eines Punktes anhand einer bekannten Entfernung und eines Richtungswinkels zu ermitteln.

Mit dem umgekehrten Problem ist alles völlig klar - zum Beispiel habe ich meine Koordinaten bestimmt und bin dann einige Zeit in einer geraden Linie gegangen und habe erneut meine Koordinaten bestimmt. Zu finden, wie viel ich geleistet habe, bedeutet, das inverse geodätische Problem zu lösen.

Das heißt: Das inverse geodätische Problem besteht darin, die Entfernung zwischen zwei Punkten mit bekannten geografischen Koordinaten zu ermitteln.

Sie können diese Probleme auf verschiedene Arten lösen, abhängig von der erforderlichen Genauigkeit und der Zeit, die Sie dafür bereit sind.

Der einfachste Weg ist sich vorzustellen, dass die Erde flach ist - das ist eine Kugel. Lass es uns versuchen.
Hier ist die Formel zur Lösung des direkten Problems ( Quelle ):

$$

$$\ phi_2 = arcsin (sin \ phi_1cos \ delta + cos \ phi_1sin \ delta cos \ theta)$$

$$

$$\ lambda_2 = \ lambda_1 + atan2 (sin \ theta sin \ delta cos \ phi_1, cos \ delta-sin \ phi_1sin \ phi_2)$$

Hier $$$\ phi_1$ , $$$\ lambda_1$ - Breitengrad und Längengrad des Startpunkts, $$$\ theta$ - Richtungswinkel, gemessen im Uhrzeigersinn von Norden (von oben gesehen), $$$\ Delta$ - Winkelabstand d / R d ist die gemessene (zurückgelegte) Distanz und R ist der Radius der Erde. $$$\ phi_2$ , $$$\ lambda_2$ - Breitengrad und Längengrad des gewünschten Punktes (derjenige, zu dem wir gekommen sind).

Um das umgekehrte Problem zu lösen, gibt es eine andere (nicht weniger einfache Formel):

$$

$$a = sin ^ 2 (\ Delta \ phi / 2) + cos \ phi_1 cos \ phi_2 sin ^ 2 (\ Delta \ lambda / 2)$$

$$

$$d = R * atan2 (\ sqrt a, \ sqrt {1-a})$$

Wo $$$\ phi_1$ , $$$\ lambda_1$ und $$$\ phi_2$ , $$$\ lambda_2$ - Koordinaten der Punkte, R - Erdradius.

Die beschriebenen Formeln heißen Haversinusgleichungen.

• In einer C # -Implementierung heißen die entsprechenden Funktionen HaversineDirect und HaversineInverse und befinden sich in Algorithms.cs .
• In einer Rust-Implementierung sind dies die Funktionen haversine_direct und haversine_inverse .
• Schließlich werden Funktionen in Matlab in separaten Dateien gespeichert, und hier sind beide Funktionen:
  HaversineDirect und HaversineInverse

Für C # werde ich die Namen der Funktionen und einen Link zu der Datei angeben, in der sie sich befinden. Für Rust - nur die Namen der Funktionen (da sich die gesamte Bibliothek in einer Datei befindet) und für Matlab - eine Verknüpfung zur entsprechenden Skriptdatei, da es in Matlab eine Funktion gibt - ein Skript.

Offensichtlich gibt es eine Art Haken: Die Erde ist keine Kugel, sondern eine Ebene, und dies muss irgendwie die Anwendbarkeit dieser Formeln und / oder die Genauigkeit der Lösung beeinflussen.

Und wirklich. Aber um dies festzustellen, müssen Sie mit etwas vergleichen.
Bereits 1975 veröffentlichte Thaddeus Vincenty eine rechnerisch effiziente Lösung von direkten und inversen geodätischen Problemen auf der Oberfläche eines Sphäroids (besser bekannt als Ellipsoid der Revolution, Genosse! Ellisoid der Rotation), die mittlerweile fast Standard ist.

Die Beschreibung der Methode device ist in einem separaten Artikel enthalten, daher beschränke ich mich darauf, Vincentis Originalarbeit und einen Online-Rechner mit einer Beschreibung des Algorithmus zuzusenden.

In der UCNLNav-Bibliothek liegt die Lösung von direkten und inversen geodätischen Problemen mit Vincenti-Formeln in den folgenden Funktionen:

• VincentyDirect und VincentyInverse in Algorithms.cs .
• Rust: vincenty_inverse und vincenty_direct
• Matlab: Nav_vincenty_direct und Nav_vincenty_inverse .

Weil Vincentis Lösung ist iterativ, dann ist die maximale Anzahl von Iterationen (it_limit) in der Parameterliste vorhanden, und die tatsächliche Anzahl von Iterationen ist in der Ergebnisliste. Es gibt auch einen Schwellenwert, der eine Stoppbedingung (Epsilon) angibt. In den meisten Fällen sind nicht mehr als 10 Iterationen erforderlich, aber für fast antipodale Punkte (wie den Nord- und Südpol) konvergiert die Methode schlecht und es können bis zu 2000 Iterationen erforderlich sein.

Der wichtigste Unterschied besteht darin, dass diese Formeln die Lösung auf einem Sphäroid ausführen und ihre Parameter auf Funktionen übertragen werden müssen. Hierfür gibt es eine einfache Struktur, die es beschreibt.

In allen Implementierungen kann eines der Standardellipsoide in einer Zeile erhalten werden. (Sehr oft wird WGS84 [https://en.wikipedia.org/wiki/World_Geodetic_System] verwendet und wir werden es als Beispiel geben):

• In C #: Algorithms.cs gibt es ein statisches Feld Algorithms.WGS84Ellipsoid - es kann an Methoden übergeben werden.
• Auf Rust:

  let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); 

• Auf Matlab:

   el = Nav_build_standard_ellipsoid('WGS84'); 

Der Name der übrigen Parameter ist offensichtlich und sollte keine Mehrdeutigkeiten verursachen.

Um zu verstehen, was es uns kostet, Lösungen für eine Kugel anstelle einer Ellipse zu verwenden, gibt es ein Skript in der Matlab-Implementierung.

In Matlab ist es wahnsinnig praktisch, alles ohne unnötige Gesten anzuzeigen. Deshalb habe ich es zu Demonstrationszwecken ausgewählt.

Die Logik seines Drehbuchs:

1. Wir nehmen einen Punkt mit beliebigen Koordinaten

 sp_lat_rad = degtorad(48.527683); sp_lon_rad = degtorad(44.558815); 

und eine beliebige Richtung (ich wählte über Westen):

 fwd_az_rad = 1.5 * pi + (rand * pi / 4 - pi / 8); 

2. Wir treten von ihm in eine immer größere Entfernung. Warum stellen wir sofort die Anzahl der Schritte und die Schrittgröße ein:

 n_samples = 10000; step_m = 1000; % meters distances = (1:n_samples) .* step_m; 

3. Für jeden Schritt lösen wir das direkte geodätische Problem auf der Kugel und auf dem Ellipsoid und erhalten den gewünschten Punkt:

 [ h_lats_rad(idx), h_lons_rad(idx) ] = Nav_haversine_direct(sp_lat_rad,... sp_lon_rad,... distances(idx),... fwd_az_rad,... el.mjsa_m); [ v_lats_rad(idx), v_lons_rad(idx), v_rev_az_rad, v_its ] = Nav_vincenty_direct(sp_lat_rad,... sp_lon_rad,... fwd_az_rad,... distances(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

4. Für jeden Schritt lösen wir inverse geodätische Probleme - wir berechnen die Abstände zwischen den auf einer Kugel und einem Ellipsoid erhaltenen Ergebnissen:

 [ v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(h_lats_rad(idx),... h_lons_rad(idx),... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

5. Für beide Methoden prüfen wir die inversen direkten Lösungen:

 [ ip_v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); ip_h_dist(idx) = Nav_haversine_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el.mjsa_m); 

Im Skript wird diese Sequenz zuerst für einen Schritt = 1000 m und dann für einen Schritt = 1 m ausgeführt.

Lassen Sie uns zunächst sehen, wie sich die Ergebnisse direkter Entscheidungen in Koordinaten (Breite und Länge) unterscheiden, für die wir die "Delta" -Vektoren berechnen, da alles in einer Zeile auf Matlab geschrieben ist:

 d_lat_deg = radtodeg(v_lats_rad - h_lats_rad); %    ( ) d_lon_deg = radtodeg(v_lons_rad - h_lons_rad); %    ( ) 

Auf der Achse wird die Abszisse logarithmisch dargestellt, weil Unsere Entfernungen variieren von 1 bis 10.000 km:

 figure semilogx(distances, d_lat_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Latitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); figure semilogx(distances, d_lon_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Longitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); 

Als Ergebnis erhalten wir solche Graphen für den Breitengrad:



Und für die Länge:



Ich verstehe graduell nicht, orientiere mich aber immer an der Methode zur Schätzung "nach Augenmaß":
1 ° von etwas ist ein Durchschnitt von 100-110 km. Und wenn der Fehler mehr als ein Millionstel oder mindestens ein Hunderttausendstel eines Grades beträgt, ist dies eine schlechte Nachricht.

Als nächstes betrachten wir die Abstände zwischen dem Startpunkt und dem Punkt, die bei jedem Schritt gemäß den Formeln für die Kugel und das Ellipsoid erhalten wurden. Wir berechnen den Abstand mit Vincentis Formeln (da dies offensichtlich genauer ist - der Autor verspricht einen Fehler in Millimetern). Diagramme in Metern und Kilometern sind viel greifbarer und vertrauter:

 figure semilogx(distances, v_dist, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Endpoint difference by Vincenty)'); xlabel('Distance, m'); ylabel('Difference, m'); 

Als Ergebnis erhalten wir folgendes Bild:



Es stellt sich heraus, dass die Methoden in Entfernungen von 10.000 km um 10 km voneinander abweichen.

Wenn jetzt alles für einen 1000-mal kleineren Schritt wiederholt wird, d.h. Wenn die gesamte Reichweite entlang der X-Achse nicht 10.000 km, sondern nur 10 km beträgt, sieht das Bild folgendermaßen aus:



Das heißt, bei einer Entfernung von 10 km laufen nur 20 Meter hoch, und bei 1-2 Metern weichen die Formeln nur bei Entfernungen von etwa 1000 Metern ab.

Die Schlussfolgerung des Kapitäns liegt auf der Hand: Wenn die Genauigkeit der Formeln mit der Lösung auf der Kugel für das Problem ausreicht, verwenden wir sie - sie sind einfacher und schneller.

Für diejenigen, für die Millimetergenauigkeit nicht ausreicht, wurde 2013 eine Arbeit veröffentlicht , die die Lösung geodätischer Probleme mit Nanometer- (!) Genauigkeit beschreibt. Ich bin mir nicht sicher, ob ich sofort herausfinden kann, wo es benötigt wird - außer bei geodätischen Vermessungen beim Bau von Gravitationswellendetektoren oder etwas völlig Fantastischem).

Gehen wir nun zu den leckersten über:

Navigationsprobleme lösen

Im Moment kann die Bibliothek feststellen:

• Die Position des Objekts nach Entfernung zu Punkten mit bekannten Koordinaten in 2D und 3D. Dies ist, was wir TOA - Ankunftszeit (oder genauer gesagt TOF - Flugzeit) nennen.
• Die Position des Objekts durch die Unterschiede in den Ankunftszeiten in 2D und 3D. Dies ist, was wir TDOA (Time Difference Of Arrival) nennen.

In der Realität messen wir immer die Reichweiten oder Ankunftszeiten eines Signals (und dementsprechend deren Differenz) mit Fehlern und Rauschen. Daher besteht die Lösung von Navigationsproblemen in den allermeisten Fällen in der Minimierung von Fehlern. Methode der kleinsten Quadrate und das ist alles .

Was minimiert werden muss, heißt Restfunktion.

Für TOA-Aufgaben sieht es so aus:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2 )} - r_i] ^ 2$$

Wo $$$\ epsilon (x, y, z)$ - der Wert der Restfunktion für einen bestimmten Punkt mit Koordinaten $$$(x, y, z)$ ; N ist die Anzahl der Kontrollpunkte mit Koordinaten $$$(x_i, y_i, z_i)$ , $$$r_i$ - gemessene Abstände von Bezugspunkten zum positionierten Objekt.

Und für TDOA-Aufgaben wie diese:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1, j = 2, i \ neq j} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2+ (z-z_i) ^ 2)} - \\ \ sqrt {(x-x_j) ^ 2 + (y-y_j) ^ 2 + (z-z_j) ^ 2)} - \ nu (t_ {Ai} -t_ {Aj})] ^ 2$$

Hier ist alles gleich, nur unterschiedliche Bezugspunktpaare und entsprechende Ankunftszeiten werden berücksichtigt $$$t_ {Ai}$ und $$$t_ {Aj}$ und $$$\ nu$ - Signalausbreitungsgeschwindigkeit.

Und so sehen diese Funktionen im Code aus:




Wie Sie sehen, arbeiten beide Funktionen mit einer variablen Anzahl von Kontrollpunkten oder Linien. Im Allgemeinen können Aufgaben unterschiedlich sein und auch Restfunktionen.

Sie können beispielsweise das Problem lösen, nicht nur den Standort, sondern auch die Ausrichtung zu bestimmen. In diesem Fall enthält die Restfunktion einen oder mehrere Winkel.

Lassen Sie uns näher auf die interne Struktur der Bibliothek eingehen

In dieser Phase arbeitet die Bibliothek mit 2D- und 3D-Aufgaben, und der Solver selbst weiß nicht und möchte nicht wissen, wie die minimierte Funktionalität aussieht. Dies wird auf folgende Weise erreicht.

Der Löser hat zwei Aspekte: 2D- und 3D-Löser, die auf der Nelder-Mead- Methode oder auch der Simplex-Methode basieren.

Da für dieses Verfahren keine Berechnung von Derivaten erforderlich ist (die sogenannte derivatfreie Minimierung ), kann der Bibliotheksbenutzer bei Bedarf seine eigenen Restfunktionen verwenden. Außerdem gibt es theoretisch keine Obergrenze für die Anzahl der zur Lösung des Problems verwendeten Kontrollpunkte.

In C # und Rust sind 2D- und 3D-Löser generische Methoden:

 public static void NLM2D_Solve<T>(Func<T[], double, double, double, double> eps, T[] baseElements,... //       : fxi[0] = eps(baseElements, xix[0], xiy[0], z); 

Ein Beispiel für den Aufruf des Solvers selbst:

 public static void TOA_NLM2D_Solve(TOABasePoint[] basePoints, double xPrev, double yPrev, double z, int maxIterations, double precisionThreshold, double simplexSize, out double xBest, out double yBest, out double radialError, out int itCnt) { NLM2D_Solve<TOABasePoint>(Eps_TOA3D, basePoints, xPrev, yPrev, z, maxIterations, precisionThreshold, simplexSize, out xBest, out yBest, out radialError, out itCnt); } 

Auf Rust ...

 pub fn nlm_2d_solve<T>(eps: Eps3dFunc<T>, base_elements: &Vec<T>... 

Alles ist identisch und stimmt mit der Syntax der Sprache überein.

In Matlabe mit seinem inhärenten Freiwilligkeitsprinzip hat der Löser selbst keine Ahnung, was die Grundelemente an ihn weitergeben - der Benutzer muss selbst sicherstellen, dass die Verknüpfung mit der Restfunktion und die Menge der an den Löser weitergegebenen Unterstützungselemente kompatibel sind:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(eps, base_elements, .... 

Dementsprechend sieht der Aufruf an den Solver folgendermaßen aus:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size) [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(@Nav_eps_toa3d, base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size); end 

Es gibt ein spezielles Matlab-Skript, um die Lösung von TOA- und TDOA-Problemen zu demonstrieren.

Die Demonstration in 2D wurde nicht zufällig ausgewählt - ich bin nicht sicher, ob ich herausfinden kann, wie die dreidimensionale Restfunktion einfach und informativ dargestellt werden kann =)

Also Zu Beginn des Skripts gibt es Parameter, die geändert werden können:

 %% parameters n_base_points = 4; %    area_width_m = 1000; %   max_depth_m = 100; %   ( Z) propagation_velocity = 1500;%     -  max_iterations = 2000; %    precision_threshold = 1E-9; %   simplex_size = 1; %      contour_levels = 32; %      range_measurements_error = 0.01; % 0.01 means 1% of corresponding slant range %    -   1% 

Die Position des gewünschten Punktes wird zufällig in dem angegebenen Bereich festgelegt:

 %% actual target location r_ = rand * area_width_m / 2; az_ = rand * 2 * pi; actual_target_x = r_ * cos(az_); actual_target_y = r_ * sin(az_); actual_target_z = rand * max_depth_m; 

Als nächstes platzieren Sie die Kontrollpunkte nach dem Zufallsprinzip, berechnen den Abstand von den gewünschten zu ihnen und zeigen alles an:

 %% base points figure hold on grid on base_points = zeros(n_base_points, 4); for n = 1:n_base_points r_ = area_width_m / 2 - rand * area_width_m / 4; az_ = (n - 1) * 2 * pi / n_base_points; base_x = r_ * cos(az_); base_y = r_ * sin(az_); base_z = rand * max_depth_m; dist_to_target = Nav_dist_3d(base_x, base_y, base_z, actual_target_x, actual_target_y, actual_target_z); base_points(n, :) = [ base_x base_y base_z dist_to_target ]; end N =1:n_base_points; plot3(actual_target_x, actual_target_y, actual_target_z,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot3(base_points(N, 1), base_points(N, 2), base_points(N, 3),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); for n = 1:n_base_points line([ actual_target_x, base_points(n, 1) ], [ actual_target_y, base_points(n, 2) ], [ actual_target_z, base_points(n, 3) ]); end view(45, 15); legend('target', 'base points'); title('Placement of base stations and the target'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); zlabel('Z coordinate, m'); 

Als Ergebnis erhalten wir folgendes Bild:



Hinzufügen von zufälligen Fehlern zu Entfernungsmessungen:

 % adding range measurement errors base_points(N, 4) = base_points(N, 4) + base_points(N, 4) *... (rand * range_measurements_error - range_measurements_error / 2); 

Wir konstruieren die Restfunktion für die ausgewählte Region mit einer bestimmten Dezimierung - andernfalls können die Berechnungen merkliche Zeit in Anspruch nehmen. Ich habe die Größe der Fläche 1000 x 1000 Meter gewählt und betrachte die Restfunktion in der gesamten Fläche nach 10 Metern:

 % error surface tiles tile_size_m = 10; n_tiles = area_width_m / tile_size_m; %% TOA solution error_surface_toa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_toa(t_x, t_y) = Nav_eps_toa3d(base_points,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf_a = [1:n_tiles] * tile_size_m - area_width_m / 2; surf(surf_a, surf_a, error_surface_toa); title('TOA solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Hier ist die Restfunktion:



Natürlich war ich ein bisschen schlau - die relativen Positionen der Kontrollpunkte und der gewünschten sind so gewählt, dass sie immer eine konvexe Figur mit dem gewünschten Punkt darin bilden. Vor allem deshalb hat die Oberfläche ein Minimum, was problemlos ist.

Ein arroganter Leser kann diese Reihenfolge ändern und versehentlich versuchen, die Ankerpunkte und den gewünschten zu setzen.

Zeigen Sie jetzt alles zusammen an. Dies ist auf der Oberfläche schwierig - unterschiedliche Werte entlang der vertikalen Achse. Daher ist es praktisch, alles auf einem zweidimensionalen Schnitt zu zeichnen:

 figure hold on contourf(surf_a, surf_a, error_surface_toa, contour_levels); plot(actual_target_x, actual_target_y,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(base_points(N, 1), base_points(N, 2),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); [ x_prev, y_prev ] = Nav_toa_circles_1d_solve(base_points, actual_target_z, pi / 180, 10, 0.1); [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, actual_target_z,... max_iterations, precision_threshold, simplex_size); plot(x_best, y_best,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); title(sprintf('TOA Solution: Residual function. Target location estimated with E_{radial} = %.3f m in %d iterations', rerr, it_cnt)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Residual function value', 'Actual target location', 'Base points', 'Estimated target location'); 

Das Ergebnis ist ungefähr so:



Der radiale Fehler wird in der Kopfzeile des Diagramms angezeigt - die Wurzel des Endwerts der Restfunktion. Die Grafik zeigt, dass der reale und der berechnete Ort in guter Übereinstimmung sind, aber die Skala erlaubt es uns nicht, zu bestimmen, wie gut.

Daher zeigen wir den berechneten Ort des gewünschten Punktes und seinen tatsächlichen Ort separat an und berechnen den Abstand zwischen ihnen:

 figure hold on grid on dx = actual_target_x - x_best; dy = actual_target_y - y_best; plot(0, 0,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(dx, dy,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); plot(-dx * 2, -dy * 2, '.w'); plot(dx * 2, dy * 2, '.w'); d_delta = Nav_dist_3d(actual_target_x, actual_target_y, actual_target_z, x_best, y_best, actual_target_z); title(sprintf('TOA Solution: Actual vs. Estimated location, distance: %.3f m', d_delta)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Actual target location', 'Estimated target location'); 

So sieht es aus:



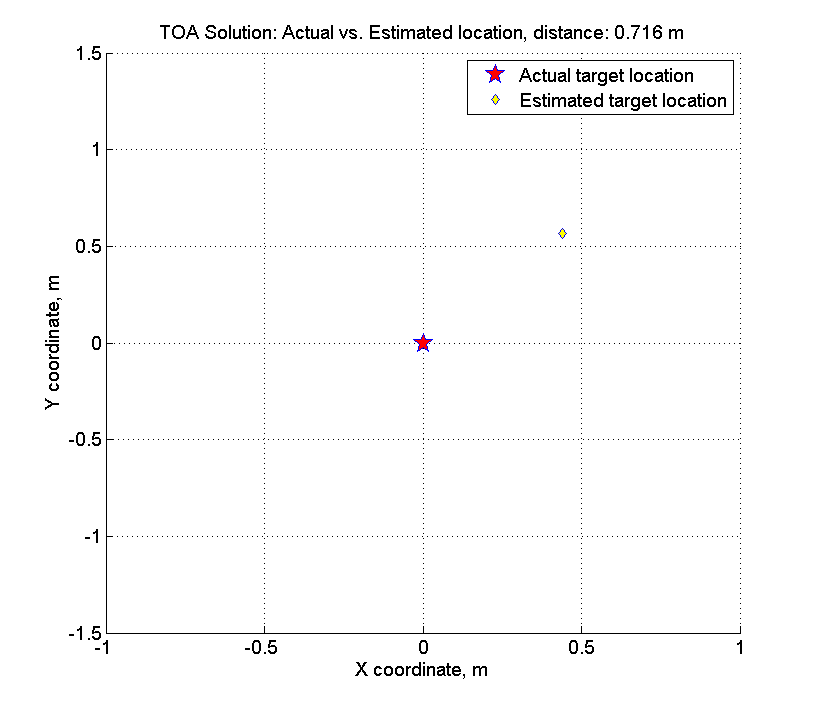
Denken Sie daran, dass wir die Amplitude eines zufälligen Fehlers haben - 1% der Reichweite, im Durchschnitt beträgt die Reichweite ~ 200-400 Meter, d. H. Die Fehleramplitude beträgt ca. 2-4 Meter. Bei der Suche nach einer Lösung haben wir einen Fehler von nur 70 Zentimetern gemacht.

Analog versuchen wir nun, das TDOA-Problem mit denselben Daten zu lösen. Dazu geben wir vor, dass wir nur die Ankunftszeiten von Signalen vom gewünschten Punkt zu den Referenzpunkten kennen (oder umgekehrt, das spielt keine Rolle) - wir teilen einfach unsere Entfernungen durch die Geschwindigkeit der Signalausbreitung - nur ihre Unterschiede und nicht die absoluten Werte sind wichtig.

 % since TDOA works with time difference of arriaval, % we must recalculate base point's distances to times base_points(N,4) = base_points(N,4) / propagation_velocity; base_lines = Nav_build_base_lines(base_points, propagation_velocity); 

Erstellen und zeichnen Sie eine Fehleroberfläche:

 error_surface_tdoa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_tdoa(t_x, t_y) = Nav_eps_tdoa3d(base_lines,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf(surf_a, surf_a, error_surface_tdoa); title('TDOA Solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Es stellt sich so etwas heraus:



Und die Ansicht von oben mit Bezugspunkten, die realen und berechneten Positionen des gewünschten Punktes:



Und im Detail die Diskrepanz zwischen dem realen und dem berechneten Ort:



In diesem speziellen Fall war die TDOA-Lösung sogar besser als die TOA-Lösung - der absolute Fehler beträgt 0,3 Meter.

Gut im Modell - Sie wissen immer genau, wo sich der gewünschte Punkt tatsächlich befindet. In der Luft ist es schlimmer - vielleicht gibt es mehrere Sichtweisen, unter Wasser haben Sie gerade etwas berechnet und das ist alles - in 99% der Fälle muss, um die Abweichung vom tatsächlichen Standort zu berechnen, auch dieser Standort zuerst berechnet werden.

Abschließend werden wir unser neues Wissen über geodätische und Navigationsaufgaben zusammenfassen.

Schlussakkord

So nah wie möglich an der realen Situation:

• Angenommen, unsere Referenzpunkte haben eingebaute GNSS-Empfänger und wir kennen nur ihre geografischen Koordinaten
• die vertikale Koordinate ist uns unbekannt (3D Problem)
• Wir messen nur die Ankunftszeiten des Signals von den Referenzpunkten auf den gewünschten oder umgekehrt

Diese Situation wurde im letzten Test in allen drei Implementierungen beschrieben. Ich habe Rust irgendwie beraubt, und ich werde das letzte Beispiel darauf analysieren.

Also der letzte Test in der Bibliothek. Als Koordinaten des gewünschten Punktes habe ich einen Ort im Park gewählt, an dem ich oft mit dem Hund spazieren gehe.

 #[test] fn test_tdoa_locate_3d() { let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); let base_number = 4; // 4   let start_base_z_m: f64 = 1.5; //  Z     let base_z_step_m = 5.0; //        5  let actual_target_lat_deg: f64 = 48.513724 // singed degrees let actual_target_lon_deg: f64 = 44.553248; // signed degrees let actual_target_z_m: f64 = 25.0; // meters - ,    ! // generate base points via Vincenty equations let mut base_points = Vec::new(); let start_dst_projection_m = 500.0; //      500  let dst_inc_step_m = 50.0; //   -  50   // azimuth step let azimuth_step_rad = PI2 / base_number as f64; //     let actual_target_lat_rad = actual_target_lat_deg.to_radians(); let actual_target_lon_rad = actual_target_lon_deg.to_radians(); // signal propagation speed let velocity_mps = 1450.0; // m/s,        //     for base_idx in 0..base_number { //        let dst_projection_m = start_dst_projection_m + dst_inc_step_m * base_idx as f64; //       let azimuth_rad = azimuth_step_rad * base_idx as f64; //        Vincenty let vd_result = vincenty_direct(actual_target_lat_rad, actual_target_lon_rad, azimuth_rad, dst_projection_m, &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); //   Z let base_z_m = start_base_z_m + base_z_step_m * base_idx as f64; //        let dz_m = actual_target_z_m - base_z_m; //      let slant_range_m = (dst_projection_m * dst_projection_m + dz_m * dz_m).sqrt(); //   .          Rust   ! base_points.push((vd_result.0.to_degrees(), vd_result.1.to_degrees(), base_z_m, slant_range_m / velocity_mps)); } //     -   NAN- let lat_prev_deg = f64::NAN; let lon_prev_deg = f64::NAN; let prev_z_m = f64::NAN; //   let tdoa_3d_result = tdoa_locate_3d(&base_points, lat_prev_deg, lon_prev_deg, prev_z_m, NLM_DEF_IT_LIMIT, NLM_DEF_PREC_THRLD, 10.0, &el, velocity_mps); //          let vi_result = vincenty_inverse(actual_target_lat_rad, actual_target_lon_rad, tdoa_3d_result.0.to_radians(), tdoa_3d_result.1.to_radians(), &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); assert!(vi_result.0 < start_dst_projection_m * 0.01, "Estimated location is farer than limit (1%): {}", vi_result.0); assert_approx_eq!(tdoa_3d_result.2, actual_target_z_m, start_dst_projection_m * 0.05); assert!(tdoa_3d_result.3 < start_dst_projection_m * 0.01, "Residual function greater than limit (1%): {}", tdoa_3d_result.3); assert!(tdoa_3d_result.4 < NLM_DEF_IT_LIMIT, "Method did not converge: iterations limit exeeded {}", tdoa_3d_result.4); } 

Als Ergebnis haben wir:
Realer Standort (Lat, Lon, Z): 48.513724 44.553248 25
Berechnete Position (Lat, Lon, Z): 48.513726 44.553252 45.6
Abstand zwischen Punkten auf der Oberfläche (m): 0,389
Differenz in der Z-Koordinate (m): 20.6

Die Planübereinstimmung ist sehr gut, der Fehler beträgt nur 40 Zentimeter und die vertikale Koordinate beträgt 20 Meter. Warum passiert das? Ich schlage vor, die Leser denken =)

PS

Die beschriebene Bibliothek ist ein rein pädagogisches Projekt, das ich weiterentwickeln und ergänzen möchte. Die Pläne beinhalten die Implementierung in C und die Erstellung einer umfassenden Dokumentation.

Lassen Sie mich diesbezüglich Abschied nehmen, danke für Ihre Aufmerksamkeit.Ich freue mich unendlich über jede Rückmeldung.
Hoffe, der Artikel und die Bibliothek werden hilfreich sein.
Melden Sie Fehler (grammatikalisch und logisch) - ich werde sie korrigieren.

PPS

Nur für den Fall, hier ist ein Link zu Online (und nicht nur) Matlab / Octave-Dolmetschern, die ich selbst benutze:

• Online Octave Compiler
• Oktave online
• GNU Octave