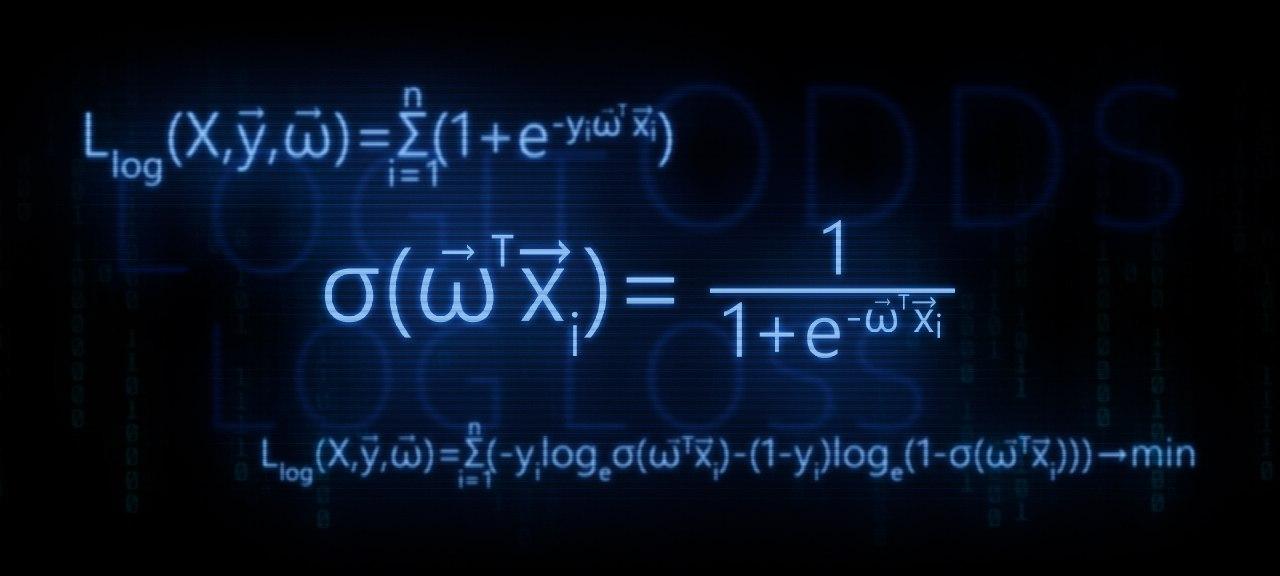
In diesem Artikel analysieren wir die theoretischen Berechnungen zur Konvertierung
der linearen Regressionsfunktion in die inverse Protokolltransformationsfunktion (mit anderen Worten die logistische Antwortfunktion) . Dann leiten wir unter Verwendung des Arsenals
der Maximum-Likelihood-Methode gemäß dem logistischen Regressionsmodell die Verlustfunktion
Logistic Loss ab , oder mit anderen Worten, wir bestimmen die Funktion, mit der die Parameter des Gewichtsvektors im logistischen Regressionsmodell ausgewählt werden
v e c w .
Die Gliederung des Artikels:
- Lassen Sie uns die einfache Beziehung zwischen zwei Variablen wiederholen
- Wir identifizieren die Notwendigkeit zur Konvertierung der linearen Regressionsfunktion f ( w , x i ) = v e c w T v e c x i auf die logistische Antwortfunktion \ sigma (\ vec {w} ^ T \ vec {x_i}) = \ frac {1} {1 + e ^ {- \ vec {w} ^ T \ vec {x_i}}\ sigma (\ vec {w} ^ T \ vec {x_i}) = \ frac {1} {1 + e ^ {- \ vec {w} ^ T \ vec {x_i}}
- Wir führen die Transformationen durch und leiten die logistische Antwortfunktion ab
- Versuchen wir zu verstehen, warum die Methode der kleinsten Quadrate bei der Auswahl von Parametern schlecht ist v e c w Logistic Loss Features
- Wir verwenden die Maximum-Likelihood-Methode , um die Parameterauswahlfunktion zu bestimmen v e c w :
5.1. Fall 1: Logistic Loss Funktion für Objekte mit der Klassenbezeichnung 0 und 1 :
Llog(X, vecy, vecw)= sum limitsni=1(−yi mkern2muloge mkern5mu sigma( vecwT vecxi)−(1−yi) mkern2muloge mkern5mu(1− sigma( vecwT vecxi))) rightarrowmin
5.2. Fall 2: Logistic Loss- Funktion für Objekte mit den Klassenbezeichnungen -1 und +1 :
Llog(X, vecy, vecw)= sum limitsni=1 mkern2Muloge mkern5Mu(1+e−yi vecwT vecxi) rightarrowmin
Der Artikel enthält zahlreiche einfache Beispiele, in denen alle Berechnungen mündlich oder auf Papier durchgeführt werden können. In einigen Fällen kann ein Taschenrechner erforderlich sein. Also mach dich bereit :)
Dieser Artikel richtet sich eher an Datenschaffende mit einem anfänglichen Kenntnisstand in den Grundlagen des maschinellen Lernens.
Der Artikel enthält auch Code zum Zeichnen von Diagrammen und Berechnungen. Der gesamte Code ist in
Python 2.7 geschrieben . Ich werde im Voraus auf die "Neuheit" der verwendeten Version eingehen. Dies ist eine der Voraussetzungen für die Teilnahme an einem bekannten Kurs von
Yandex auf der nicht weniger bekannten Online-Plattform für Online-Schulungen
Coursera . Wie Sie vielleicht annehmen, wurde das Material auf der Grundlage dieses Kurses erstellt.
01. Gerade Linie
Es ist durchaus sinnvoll, sich die Frage zu stellen: Wo ist die direkte Beziehung und die logistische Regression?
Alles ist einfach! Die logistische Regression ist eines der Modelle, die zum linearen Klassifikator gehören. Mit einfachen Worten, das Ziel eines linearen Klassifikators ist die Vorhersage von Zielwerten
y aus Variablen (Regressoren)
X . Es wird angenommen, dass die Beziehung zwischen den Zeichen
X und Zielwerte
y linear. Daher ist der Name des Klassifikators selbst linear. Wenn sehr grob verallgemeinert, basiert das logistische Regressionsmodell auf der Annahme, dass es einen linearen Zusammenhang zwischen Merkmalen gibt
X und Zielwerte
y . Hier ist es - eine Verbindung.
Das Studio ist das erste Beispiel, und das zu Recht, für die einfache Abhängigkeit der untersuchten Mengen. Bei der Erstellung des Artikels bin ich auf ein Beispiel
gestoßen , das bereits
Halsschmerzen verursacht hat - die Abhängigkeit der Stromstärke von der Spannung
(„Applied Regression Analysis“, N. Draper, G. Smith) . Hier werden wir es auch betrachten.
In Übereinstimmung mit dem
Ohmschen Gesetz:I=U/R wo
I - aktuelle Stärke
U - Spannung
R - Widerstand.
Wenn wir das
Ohmsche Gesetz nicht wüssten, könnten wir die Abhängigkeit empirisch finden, indem wir sie ändern
U und messen
I während der Unterstützung
R behoben. Dann würden wir das Abhängigkeitsdiagramm sehen
I von
U Gibt eine mehr oder weniger gerade Linie durch den Ursprung. Wir haben "mehr oder weniger" gesagt, weil unsere Messungen, obwohl die Abhängigkeit tatsächlich genau ist, möglicherweise kleine Fehler enthalten und daher die Punkte in der Grafik möglicherweise nicht genau auf die Linie fallen, sondern zufällig darum herum verstreut werden.
Grafik 1 „Abhängigkeit
I von
U "
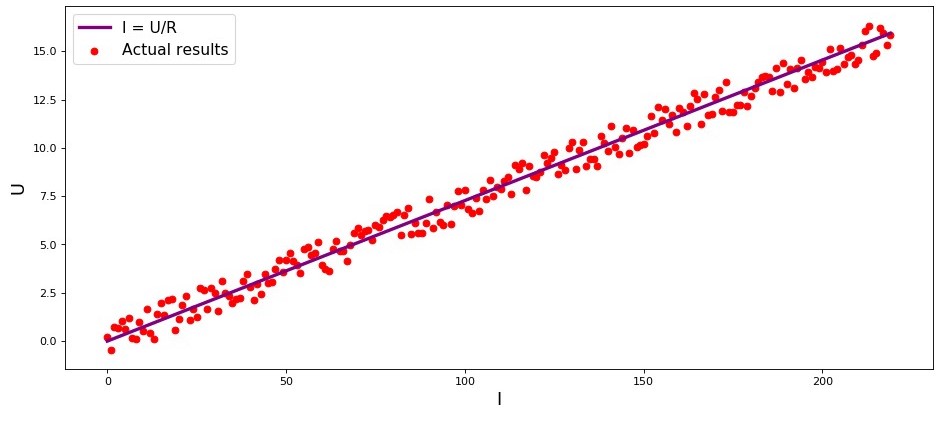
Grafik-Rendering-Codeimport matplotlib.pyplot as plt %matplotlib inline import numpy as np import random R = 13.75 x_line = np.arange(0,220,1) y_line = [] for i in x_line: y_line.append(i/R) y_dot = [] for i in y_line: y_dot.append(i+random.uniform(-0.9,0.9)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(x_line,y_line,color = 'purple',lw = 3, label = 'I = U/R') plt.scatter(x_line,y_dot,color = 'red', label = 'Actual results') plt.xlabel('I', size = 16) plt.ylabel('U', size = 16) plt.legend(prop = {'size': 14}) plt.show()
02. Notwendigkeit von Transformationen der linearen Regressionsgleichung
Betrachten Sie ein anderes Beispiel. Stellen Sie sich vor, wir arbeiten in einer Bank und stehen vor der Aufgabe, die Wahrscheinlichkeit der Rückzahlung eines Kredits durch einen Kreditnehmer in Abhängigkeit von einigen Faktoren zu bestimmen. Um die Aufgabe zu vereinfachen, berücksichtigen wir nur zwei Faktoren: das monatliche Gehalt des Kreditnehmers und die monatliche Zahlung für die Rückzahlung des Kredits.
Die Aufgabe ist sehr bedingt, aber mit diesem Beispiel können wir verstehen, warum es nicht ausreicht,
die lineare Regressionsfunktion zu verwenden, um sie zu lösen, und wir werden auch herausfinden, welche Transformationen mit der Funktion durchgeführt werden müssen.
Wir kehren zum Beispiel zurück. Es wird davon ausgegangen, dass der Kreditnehmer umso mehr monatliche Anweisungen zur Rückzahlung des Kredits erhält, je höher das Gehalt ist. Gleichzeitig ist diese Abhängigkeit für einen bestimmten Bereich von Gehältern ziemlich linear. Nehmen Sie zum Beispiel einen Gehaltsbereich von 60.000 € bis 200.000 € und nehmen Sie an, dass in dem angegebenen Gehaltsbereich die Abhängigkeit der Höhe der monatlichen Zahlung von der Höhe des Gehalts linear ist. Angenommen, für die angegebene Lohnspanne hat sich herausgestellt, dass das Verhältnis von Gehalt zu Zahlung nicht unter 3 sinken kann und dass der Kreditnehmer immer noch 5.000 € in Reserve haben sollte. Und nur in diesem Fall gehen wir davon aus, dass der Kreditnehmer den Kredit an die Bank zurückgibt. Dann hat die lineare Regressionsgleichung die Form:
f(w,xi)=w0+w1xi1+w2xi2,wo
w0=−5.000 ,
w1=1 ,
w2=−3 ,
xi1 -
Gehalt i Kreditnehmer
xi2 -
Darlehenszahlung i Kreditnehmer.
Ersetzen der Gehalts- und Darlehenszahlung durch feste Parameter in der Gleichung
vecw Sie können entscheiden, ob Sie ein Darlehen gewähren oder ablehnen.
Mit Blick auf die Zukunft stellen wir fest, dass für bestimmte Parameter
vecw Die in
der logistischen Antwortfunktion verwendete
lineare Regressionsfunktion führt zu großen Werten, die die Berechnung der Rückzahlungswahrscheinlichkeiten für Kredite erschweren. Daher wird vorgeschlagen, unsere Koeffizienten beispielsweise um das 25.000-fache zu reduzieren. Aus dieser Umrechnung in Quoten ergibt sich keine Änderung der Entscheidung zur Gewährung eines Darlehens. Erinnern wir uns an diesen Moment für die Zukunft, und um noch klarer zu werden, worüber wir sprechen, werden wir die Situation mit drei potenziellen Kreditnehmern betrachten.
Tabelle 1 "Potenzielle Kreditnehmer"
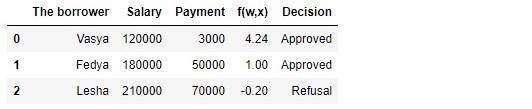
Code zum Generieren der Tabelle import pandas as pd r = 25000.0 w_0 = -5000.0/r w_1 = 1.0/r w_2 = -3.0/r data = {'The borrower':np.array(['Vasya', 'Fedya', 'Lesha']), 'Salary':np.array([120000,180000,210000]), 'Payment':np.array([3000,50000,70000])} df = pd.DataFrame(data) df['f(w,x)'] = w_0 + df['Salary']*w_1 + df['Payment']*w_2 decision = [] for i in df['f(w,x)']: if i > 0: dec = 'Approved' decision.append(dec) else: dec = 'Refusal' decision.append(dec) df['Decision'] = decision df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision']]
Laut Tabelle möchte Vasya mit einem Gehalt von 120.000 € ein solches Darlehen erhalten, um es bei 3.000 € monatlich zurückzuzahlen. Um das Darlehen zu genehmigen, haben wir festgelegt, dass Vasyas Gehalt dreimal so hoch sein sollte wie die Zahlung, und dass immer noch 5.000 Pence zur Verfügung stehen. Vasya erfüllt diese Anforderung:
120.000−3∗3.000−5.000=106.000 . Es bleiben sogar 106.000 P übrig. Trotz der Tatsache, dass bei der Berechnung
f(w,xi) Wir haben die Gewinnchancen reduziert
vecw 25.000 Mal war das Ergebnis das gleiche - das Darlehen kann genehmigt werden. Fedya wird auch einen Kredit erhalten, aber Lesha wird, trotz der Tatsache, dass er am meisten erhält, seinen Appetit zügeln müssen.
Lassen Sie uns einen Zeitplan für diesen Fall zeichnen.
Grafik 2 „Klassifizierung der Kreditnehmer“
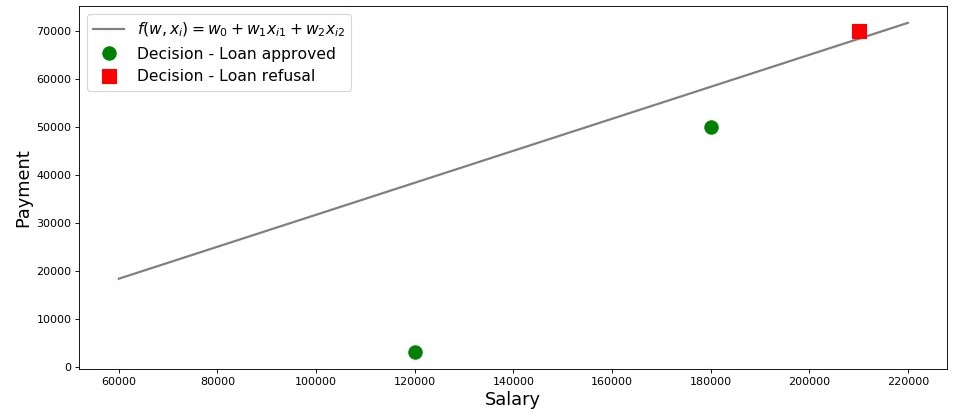
Code zum Plotten salary = np.arange(60000,240000,20000) payment = (-w_0-w_1*salary)/w_2 fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(salary, payment, color = 'grey', lw = 2, label = '$f(w,x_i)=w_0 + w_1x_{i1} + w_2x_{i2}$') plt.plot(df[df['Decision'] == 'Approved']['Salary'], df[df['Decision'] == 'Approved']['Payment'], 'o', color ='green', markersize = 12, label = 'Decision - Loan approved') plt.plot(df[df['Decision'] == 'Refusal']['Salary'], df[df['Decision'] == 'Refusal']['Payment'], 's', color = 'red', markersize = 12, label = 'Decision - Loan refusal') plt.xlabel('Salary', size = 16) plt.ylabel('Payment', size = 16) plt.legend(prop = {'size': 14}) plt.show()
Also, unsere Linie, aufgebaut nach der Funktion
f(w,xi)=w0+w1xi1+w2xi2 trennt die "schlechten" Kreditnehmer von den "guten". Diejenigen Kreditnehmer, deren Wünsche nicht mit Chancen übereinstimmen, befinden sich über der direkten Linie (Lesha), diejenigen, die in der Lage sind, den Kredit gemäß den Parametern unseres Modells zurückzuzahlen, befinden sich unter der direkten Linie (Vasya und Fedya). Ansonsten können wir das sagen - unsere Linie unterteilt die Kreditnehmer in zwei Klassen. Wir bezeichnen sie wie folgt: für die Klasse
+1 Klassifizieren Sie die Kreditnehmer, die den Kredit wahrscheinlich an die Klasse zurückzahlen
−1 oder
0 wir werden diejenigen kreditnehmer zuweisen, die höchstwahrscheinlich nicht in der lage sind, das darlehen zurückzuzahlen.
Fassen Sie die Schlussfolgerungen aus diesem einfachen Beispiel zusammen. Nimm einen Punkt
M(x1,x2) und Ersetzen der Koordinaten des Punktes in der entsprechenden Gleichung der Linie
f(w,xi)=w0+w1xi1+w2xi2 Betrachten Sie drei Optionen:
- Befindet sich der Punkt unter der Linie und ordnen wir ihn der Klasse zu +1 , dann der Wert der Funktion f(w,xi)=w0+w1xi1+w2xi2 wird positiv aus 0 vorher + infty . Wir können also davon ausgehen, dass die Wahrscheinlichkeit einer Kreditrückzahlung innerhalb liegt (0.5,1] . Je größer der Wert der Funktion ist, desto höher ist die Wahrscheinlichkeit.
- Wenn der Punkt über der Linie liegt und wir ihn auf die Klasse beziehen −1 oder 0 , dann wird der Wert der Funktion von negativ sein 0 vorher − infty . Dann gehen wir davon aus, dass die Wahrscheinlichkeit einer Rückzahlung der Schulden innerhalb liegt [0,0.5) und je größer der Wert der Funktion modulo ist, desto höher ist unser Vertrauen.
- Der Punkt liegt auf einer geraden Linie an der Grenze zwischen zwei Klassen. In diesem Fall der Wert der Funktion f(w,xi)=w0+w1xi1+w2xi2 wird gleich sein 0 und die Wahrscheinlichkeit der Rückzahlung des Darlehens ist gleich 0.5 .
Stellen Sie sich vor, wir haben nicht zwei Faktoren, sondern zehn, Kreditnehmer nicht drei, sondern Tausende. Dann haben wir anstelle einer geraden Linie eine
m-dimensionale Ebene und Koeffizienten
w Wir werden nicht von der Obergrenze genommen, sondern nach allen Regeln zurückgezogen, sondern auf der Grundlage von gesammelten Daten über Kreditnehmer, die das Darlehen zurückgegeben haben oder nicht zurückgegeben haben. Und wirklich, wohlgemerkt, wir wählen jetzt Kreditnehmer mit bereits bekannten Quoten aus
w . Tatsächlich besteht die Aufgabe des logistischen Regressionsmodells darin, die Parameter genau zu bestimmen
w bei dem der Wert der Verlustfunktion
Logistic Loss auf ein Minimum tendiert. Aber wie wird der Vektor berechnet
vecw finden wir noch im 5. Abschnitt des Artikels heraus. In der Zwischenzeit kehren wir in das gelobte Land zurück - zu unserem Bankier und seinen drei Kunden.
Dank der Funktion
f(w,xi)=w0+w1xi1+w2xi2 Wir wissen, wem ein Kredit gewährt werden kann und wer abgelehnt werden muss. Sie können jedoch nicht mit solchen Informationen zum Direktor gehen, da er die Wahrscheinlichkeit der Rückzahlung des Kredits von jedem Kreditnehmer bei uns erhalten wollte. Was zu tun ist? Die Antwort ist einfach - wir müssen die Funktion irgendwie transformieren
f(w,xi)=w0+w1xi1+w2xi2 deren Werte liegen im Bereich
(− infty,+ infty) auf eine Funktion, deren Werte im Bereich liegen
[0,1] . Und eine solche Funktion gibt es, sie heißt
logistische Antwortfunktion oder Reverse-Logit-Konvertierung . Treffen Sie:
\ sigma (\ vec {w} ^ T \ vec {x_i}) = \ frac {1} {1 + e ^ {- \ vec {w} ^ T \ vec {x_i}}
Schauen wir uns die Schritte an, um
die logistische Antwortfunktion zu erhalten . Beachten Sie, dass wir in die entgegengesetzte Richtung gehen werden, d. H. wir gehen davon aus, dass wir den wahrscheinlichkeitswert kennen, der im bereich von liegt
0 vorher
1 und dann werden wir diesen Wert über den gesamten Zahlenbereich von "spinnen"
− infty vorher
+ infty .
03. Geben Sie die logistische Antwortfunktion aus
Schritt 1. Übertragen Sie die Wahrscheinlichkeitswerte in den Bereich [0,+ infty)
Zum Zeitpunkt der Funktionsumwandlung
f(w,xi)=w0+w1xi1+w2xi2 auf
die logistische Antwortfunktion \ sigma (\ vec {w} ^ T \ vec {x_i}) = \ frac {1} {1 + e ^ {\ vec {w} ^ T \ vec {x_i}} Wir lassen unseren Kreditanalysten in Ruhe und gehen stattdessen die Buchmacher durch. Nein, wir machen natürlich keine Wetten, alles, was uns interessiert, ist die Bedeutung des Ausdrucks, zum Beispiel eine Chance von 4 zu 1. Die Gewinnchancen, die allen Wettspielern bekannt sind, sind das Verhältnis von „Erfolgen“ zu „Misserfolgen“. Bei den Wahrscheinlichkeiten handelt es sich um die Wahrscheinlichkeit des Eintretens eines Ereignisses geteilt durch die Wahrscheinlichkeit, dass das Ereignis nicht eintritt. Wir schreiben die Formel für die Chance eines Ereignisses
(Odds+) :
odds+= fracp+1−p+
wo
p+ - Eintrittswahrscheinlichkeit eines Ereignisses,
(1−p+) - Wahrscheinlichkeit des NICHT-Auftretens eines Ereignisses
Wenn zum Beispiel die Wahrscheinlichkeit, dass ein junges, starkes und temperamentvolles Pferd mit dem Spitznamen "Veterok" bei den Rennen eine alte und schlaffe alte Frau mit dem Spitznamen "Matilda" schlägt, gleich ist
0.8 , dann sind die Erfolgschancen von Veterka
4 zu
1(0.8/(1−0.8)) und umgekehrt, wenn wir die Chancen kennen, wird es uns nicht schwer fallen, die Wahrscheinlichkeit zu berechnen
p+ :
fracp+1−p+=4 mkern15mu Longrightarrow mkern15mup+=4(1−p+) mkern15mu Longrightarrow mkern15mu5p+=4 mkern15mu Longrightarrow mkern15mup+=0.8Auf diese Weise haben wir gelernt, Wahrscheinlichkeit in Gewinnchancen zu „übersetzen“, aus denen Werte abgeleitet werden
0 vorher
+ infty . Lassen Sie uns noch einen Schritt weiter gehen und lernen, wie man die Wahrscheinlichkeit auf die gesamte Zahlenreihe von „umrechnet“
− infty vorher
+ infty .
Schritt 2. Wir übersetzen die Wahrscheinlichkeitswerte in den Bereich (− infty,+ infty)
Dieser Schritt ist sehr einfach - wir prologieren die Gewinnchancen basierend auf der Euler-Zahl
e und bekomme:
f(w,xi)= vecwT vecx=ln(Gewinnchancen+)
Jetzt wissen wir, dass wenn
p+=0.8 Berechnen Sie dann den Wert
f(w,xi) es wird sehr einfach sein und außerdem sollte es positiv sein:
f(w,xi)=ln(Gewinnchancen+)=ln(0,8/0,2)=ln(4) ca.+1,38629 . So ist es.
Aus Neugier überprüfen wir, ob
p+=0,2 dann erwarten wir einen negativen Wert
f(w,xi) . Wir prüfen:
f(w,xi)=ln(0,2/0,8)=ln(0,25) ca.−1,38629 . Alles ist richtig.
Jetzt wissen wir, wie man den Wahrscheinlichkeitswert von übersetzt
0 vorher
1 auf der ganzen nummer zeile ab
− infty vorher
+ infty . Im nächsten Schritt machen wir das Gegenteil.
In der Zwischenzeit stellen wir fest, dass nach den Regeln des Logarithmus der Wert der Funktion bekannt ist
f(w,xi) können Sie die Gewinnchancen berechnen:
odds+=ef(w,xi)=e vecwT vecx
Diese Methode zur Ermittlung der Chancen wird sich im nächsten Schritt als nützlich erweisen.
Schritt 3. Wir leiten eine Formel zur Bestimmung ab p+
Also haben wir gelernt, zu wissen
p+ Funktionswerte finden
f(w,xi) . Tatsächlich brauchen wir jedoch genau das Gegenteil - den Wert zu kennen
f(w,xi) zu finden
p+ . Dazu wenden wir uns einem Konzept wie der Umkehrfunktion von Chancen zu, nach dem:
p+= fracodds+1+odds+
In dem Artikel werden wir die obige Formel nicht ableiten, sondern die Zahlen aus dem obigen Beispiel überprüfen. Wir wissen, dass mit einer Quote von 4 zu 1 (
odds+=$ ) beträgt die Eintrittswahrscheinlichkeit eines Ereignisses 0,8 (
p+=0.8 ) Nehmen wir eine Substitution vor:
p+= frac41+4=0.8 . Dies stimmt mit unseren früher durchgeführten Berechnungen überein. Wir ziehen weiter.
Im letzten Schritt haben wir daraus geschlossen
odds+=e vecwT vecx Dies bedeutet, dass Sie die umgekehrte Funktion der Gewinnchancen ersetzen können. Wir bekommen:
p_ + = \ frac {e ^ {\ vec {w} ^ T \ vec {x}}} {1 + e ^ {\ vec {w} ^ T \ vec {x}}
Teilen Sie sowohl den Zähler als auch den Nenner durch
e vecwT vecx dann:
p+= frac11+e− vecwT vecx= sigma( vecwT vecx)
Um sicherzustellen, dass wir nirgendwo einen Fehler gemacht haben, führen wir für jeden Feuerwehrmann eine weitere kleine Überprüfung durch. In Schritt 2 sind wir für
p+=0.8 bestimmt das
f(w,xi) ca.+1.38629 . Ersetzen Sie dann den Wert
f(w,xi) in der logistischen Antwortfunktion erwarten wir zu erhalten
p+=0.8 . Ersetze und erhalte:
p+= frac11+e−1.38629=0.8Herzlichen Glückwunsch, lieber Leser, wir haben gerade die logistische Reaktionsfunktion entwickelt und getestet. Schauen wir uns den Funktionsgraphen an.
Grafik 3 „Logistische Reaktionsfunktion“

Code zum Plotten import math def logit (f): return 1/(1+math.exp(-f)) f = np.arange(-7,7,0.05) p = [] for i in f: p.append(logit(i)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(f, p, color = 'grey', label = '$ 1 / (1+e^{-w^Tx_i})$') plt.xlabel('$f(w,x_i) = w^Tx_i$', size = 16) plt.ylabel('$p_{i+}$', size = 16) plt.legend(prop = {'size': 14}) plt.show()
In der Literatur finden Sie auch den Namen dieser Funktion als
Sigmoidfunktion . Die Grafik zeigt deutlich, dass die Hauptänderung der Wahrscheinlichkeit, dass ein Objekt zu einer Klasse gehört, in einem relativ kleinen Bereich auftritt
f(w,xi) irgendwo aus
−4 vorher
+4 .
Ich schlage vor, zu unserem Kreditanalysten zurückzukehren und ihm bei der Berechnung der Rückzahlungswahrscheinlichkeit von Krediten zu helfen, da er sonst das Risiko eingeht, keinen Bonus zu erhalten :)
Tabelle 2 "Potentielle Kreditnehmer"
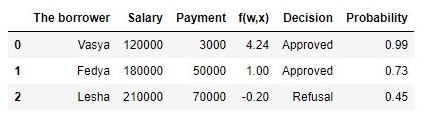
Code zum Generieren der Tabelle proba = [] for i in df['f(w,x)']: proba.append(round(logit(i),2)) df['Probability'] = proba df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision', 'Probability']]
Wir haben also die Wahrscheinlichkeit der Rückzahlung des Kredits ermittelt. Alles in allem scheint dies wahr zu sein.
In der Tat liegt die Wahrscheinlichkeit, dass Vasya mit einem Gehalt von 120.000 € der Bank 3.000 € monatlich geben kann, nahe bei 100%. Übrigens müssen wir verstehen, dass die Bank Lesha auch dann einen Kredit gewähren kann, wenn die Bank beispielsweise vorsieht, Kunden mit einer Wahrscheinlichkeit von mehr als 0,3 Rückzahlungen des Kredits einen Kredit zu gewähren. In diesem Fall bildet die Bank eine größere Reserve für mögliche Verluste.
Es ist auch anzumerken, dass das Verhältnis von Gehalt zu Zahlung von mindestens 3 und mit einer Marge von 5.000 € von der Obergrenze abgezogen wurde. Daher konnten wir den Gewichtsvektor nicht in seiner ursprünglichen Form verwenden
vecw=(−5000,1,−3) . Wir mussten die Koeffizienten stark reduzieren, und in diesem Fall haben wir jeden Koeffizienten durch 25.000 geteilt, das heißt, wir haben das Ergebnis angepasst. Dies geschah jedoch absichtlich, um das Verständnis des Materials in der Anfangsphase zu vereinfachen. Im Leben müssen wir die Koeffizienten nicht erfinden und anpassen, sondern sie finden. In den nächsten Abschnitten des Artikels werden wir die Gleichungen ableiten, mit denen die Parameter ausgewählt werden
vecw .
04. Methode der kleinsten Quadrate zur Bestimmung des Gewichtsvektors vecw in der logistischen Antwortfunktion
Wir kennen bereits eine solche Methode zur Auswahl eines Gewichtsvektors
vecw als
Methode der kleinsten Fehlerquadrate (Least Squares Method, OLS) und warum verwenden wir sie dann nicht bei Problemen mit der binären Klassifikation? In der Tat verhindert nichts die Verwendung von
MNCs , nur diese Methode bei Klassifizierungsproblemen liefert weniger genaue Ergebnisse als der
logistische Verlust . Dafür gibt es eine theoretische Begründung. Beginnen wir mit einem einfachen Beispiel.
Angenommen, unsere Modelle (mit
MSE und
Logistic Loss ) haben bereits mit der Auswahl des Gewichtsvektors begonnen
vecw und wir haben die Berechnung irgendwann abgebrochen. Es ist egal, ob in der Mitte, am Ende oder am Anfang, die Hauptsache ist, dass wir bereits einige Werte des Gewichtsvektors haben und in diesem Schritt den Gewichtsvektor annehmen
vecw Für beide Modelle gibt es keine Unterschiede. Dann nehmen wir die erhaltenen Gewichte und setzen sie in
die logistische Antwortfunktion ein (
frac11+e− vecwT vecx ) für ein Objekt, das zur Klasse gehört
+1 . Wir werden zwei Fälle untersuchen, in denen unser Modell in Übereinstimmung mit dem ausgewählten Gewichtsvektor stark verwechselt wird und umgekehrt - das Modell ist fest davon überzeugt, dass das Objekt zur Klasse gehört
+1 . Mal sehen, welche Bußgelder "ausgestellt" werden, wenn
MNCs und
Logistic Loss verwendet werden .
Code zur Berechnung von Bußgeldern in Abhängigkeit von der verwendeten Verlustfunktion Der Fall mit einem groben Fehler - das Modell klassifiziert das Objekt
+1 mit einer Wahrscheinlichkeit von 0,01
Die Strafe bei der Verwendung von
OLS ist:
MSE=(y−p+)=(1−0,01)2=0,9801Die Strafe bei Verwendung von
Logistic Loss ist:
LogLoss=loge(1+e−yf(w,x))=loge(1+e−1(−4,595...)) ca.4,605Fall mit starker Sicherheit - das Modell klassifiziert das Objekt
+1 mit einer Wahrscheinlichkeit von 0,99
Die Strafe bei der Verwendung von
OLS ist:
MSE=(1−0,99)2=$0,000Die Strafe bei Verwendung von
Logistic Loss ist:
LogLoss=loge(1+e−4.595...) ca.0,01Dieses Beispiel zeigt deutlich, dass bei einem schwerwiegenden Fehler das Modell durch die Funktion "
Log Loss loss" (
Protokollverlustverlust) erheblich stärker
beeinträchtigt wird als durch
MSE . Lassen Sie uns nun verstehen, welche theoretischen Voraussetzungen für die Verwendung der Funktion
Log Loss loss bei Klassifizierungsproblemen bestehen.
05. Maximale Glaubwürdigkeit und logistische Regression
Wie zu Beginn versprochen, enthält der Artikel viele einfache Beispiele. Das Studio hat ein anderes Beispiel und die alten Gäste sind die Kreditnehmer der Bank: Vasya, Fedya und Lesha.
Lassen Sie sich vor der Entwicklung eines Beispiels für jeden Feuerwehrmann daran erinnern, dass es sich im Leben um ein Trainingsmuster von Tausenden oder Millionen von Objekten mit Dutzenden oder Hunderten von Zeichen handelt. Hier werden die Zahlen jedoch so genommen, dass sie leicht in den Kopf eines unerfahrenen Datentests passen.
Wir kehren zum Beispiel zurück. Stellen Sie sich vor, der Direktor der Bank beschloss, allen Bedürftigen einen Kredit zu gewähren, obwohl der Algorithmus vorschlug, ihn nicht an Lesha weiterzugeben. So verging genug Zeit und wir wurden uns bewusst, welcher der drei Helden das Darlehen zurückzahlte und wer nicht. Was zu erwarten war: Vasya und Fedya zahlten den Kredit aus, Alex jedoch nicht. Stellen wir uns nun vor, dass dieses Ergebnis eine neue Trainingsstichprobe für uns sein wird und gleichzeitig alle Daten zu den Faktoren, die die Wahrscheinlichkeit der Kreditrückzahlung beeinflussen (Kreditnehmergehalt, monatlicher Zahlungsbetrag), verschwunden zu sein scheinen. Dann können wir intuitiv davon ausgehen, dass nicht jeder dritte Kreditnehmer einen Kredit an die Bank zurückgibt, oder mit anderen Worten, die Wahrscheinlichkeit, dass ein Kredit vom nächsten Kreditnehmer zurückgegeben wird
p= frac23 . Diese intuitive Annahme hat theoretische Bestätigung und basiert auf der
Maximum-Likelihood-Methode , die in der Literatur häufig als
Maximum-Likelihood-Prinzip bezeichnet wird .
Machen Sie sich zunächst mit dem konzeptionellen Apparat vertraut.
Die Wahrscheinlichkeit einer
Probe ist die Wahrscheinlichkeit, eine solche Probe zu erhalten, genau solche Beobachtungen / Ergebnisse zu erhalten, d.h. Das Produkt aus den Wahrscheinlichkeiten für das Erhalten der einzelnen Ergebnisse der Stichprobe (beispielsweise wurde das Darlehen von Vasya, Feday und Lesha gleichzeitig zurückgezahlt oder nicht zurückgezahlt).
Die Wahrscheinlichkeitsfunktion verknüpft die Wahrscheinlichkeit einer Stichprobe mit den Werten der Verteilungsparameter.
In unserem Fall ist die Trainingsstichprobe ein verallgemeinertes Bernoulli-Schema, bei dem eine Zufallsvariable nur zwei Werte annimmt:
1 oder
0 . Daher kann die Wahrscheinlichkeit der Stichprobe als Funktion der Wahrscheinlichkeit des Parameters geschrieben werden
p wie folgt:
P( mkern5mu vecy mkern5mu| mkern5mup)= prod limits3i=1pyi(1−p)(1−yi) mkern5mu= mkern5mup1(1−p)1−1 centerdotp1(1−p)1−1 centerdotp0(1−p)1−0 mkern5mu== mkern5mup centerdotp centerdot(1−p) mkern5mu= mkern5mup2(1−p)Der obige Datensatz kann wie folgt interpretiert werden. Die gemeinsame Wahrscheinlichkeit, dass Vasya und Fedya das Darlehen zurückzahlen, ist gleich
p c e n t e r d o t p = p 2 ist die Wahrscheinlichkeit, dass Alex das Darlehen NICHT zurückzahlt
1 - p (da es sich NICHT um die Rückzahlung des Darlehens handelte), ist daher die gemeinsame Wahrscheinlichkeit aller drei Ereignisse
p 2 ( 1 - p ) .
Die Maximum-Likelihood- Methode ist eine Methode zum Schätzen eines unbekannten Parameters durch Maximieren
der Likelihood-Funktion .
In unserem Fall müssen wir einen solchen Wert finden p bei denenP (→ y|p ) = p 2 ( 1 - p ) erreicht ein Maximum.Woher kommt die Idee, nach dem Wert eines unbekannten Parameters zu suchen, bei dem die Wahrscheinlichkeitsfunktion ein Maximum erreicht? Die Ursprünge der Idee liegen in der Vorstellung, dass die Stichprobe die einzige uns zur Verfügung stehende Wissensquelle über die Gesamtbevölkerung ist. Alles, was wir über die Bevölkerung wissen, ist in der Stichprobe dargestellt. Daher können wir nur sagen, dass die Stichprobe die genaueste Darstellung der Bevölkerung ist, die uns zur Verfügung steht. Daher müssen wir einen Parameter finden, bei dem die verfügbare Stichprobe die wahrscheinlichste ist.Offensichtlich haben wir es mit einem Optimierungsproblem zu tun, bei dem es erforderlich ist, den Extrempunkt einer Funktion zu finden. Um den Extrempunkt zu finden, ist es notwendig, eine Bedingung erster Ordnung zu berücksichtigen, dh die Ableitung der Funktion mit Null gleichzusetzen und die Gleichung für den gewünschten Parameter zu lösen. Die Suche nach der Ableitung des Produkts einer großen Anzahl von Faktoren kann jedoch langwierig sein, weshalb es eine spezielle Technik gibt, um dies zu vermeiden - den Übergang zum Logarithmus der Wahrscheinlichkeitsfunktion . Warum ist ein solcher Übergang möglich? Wir achten darauf, dass wir nicht das Extrem der Funktion selbst suchenP (→ y|p ) und der Extrempunkt, dh der Wert des unbekannten Parametersp bei denenP (→ y|p ) erreicht ein Maximum. Beim Übergang zum Logarithmus ändert sich der Extrempunkt nicht (obwohl sich das Extrem selbst unterscheidet), da der Logarithmus eine monotone Funktion ist. Lassen Sie uns in Übereinstimmung mit den vorstehenden Ausführungen unser Beispiel für Kredite an Vasya, Fedi und Lesha weiterentwickeln. Gehen wir zunächst zumLogarithmus der Wahrscheinlichkeitsfunktion über:l o g P (→ y|p )=l o g p 2 ( 1 - p )=2 l o g p + l o g ( 1 - p ) Nun können wir den Ausdruck leicht unterscheiden durchp :
∂ l o g P (→ y|p )∂ p=∂∂ p (2logp+log(1-p))=2p -11 - p Und schließlich betrachten wir die Bedingung erster Ordnung - wir setzen die Ableitung der Funktion gleich Null:2p -11 - p =0⟹2p =11 - p⟹2 ( 1 - p ) = p⟹p = 23 Unsere intuitive Einschätzung der Wahrscheinlichkeit einer Kreditrückzahlungp = 23 wurde theoretisch begründet. Großartig, aber was machen wir jetzt mit diesen Informationen? Wenn wir davon ausgehen, dass jeder dritte Kreditnehmer kein Geld an die Bank zurückgibt, wird diese unweigerlich bankrott gehen. Und so ist es, aber nur bei der Einschätzung der Rückzahlungswahrscheinlichkeit eines Kredits gleich23 Die Faktoren, die die Rückzahlung des Kredits beeinflussten, haben wir nicht berücksichtigt: das Gehalt des Kreditnehmers und die Höhe der monatlichen Zahlung. Denken Sie daran, dass wir zuvor die Wahrscheinlichkeit der Rückzahlung eines Kredits durch jeden Kunden berechnet haben, wobei genau diese Faktoren berücksichtigt wurden. Es ist logisch, dass die Wahrscheinlichkeiten, die wir erhalten haben, von der Konstanten gleich verschieden sind23 .
Lassen Sie uns die Wahrscheinlichkeit der Stichproben bestimmen:Code zur Berechnung der Wahrscheinlichkeit von Stichproben from functools import reduce def likelihood(y,p): line_true_proba = [] for i in range(len(y)): ltp_i = p[i]**y[i]*(1-p[i])**(1-y[i]) line_true_proba.append(ltp_i) likelihood = [] return reduce(lambda a, b: a*b, line_true_proba) y = [1.0,1.0,0.0] p_log_response = df['Probability'] const = 2.0/3.0 p_const = [const, const, const] print ' p=2/3:', round(likelihood(y,p_const),3) print '****************************************************************************************************' print ' p:', round(likelihood(y,p_log_response),3)
Die Wahrscheinlichkeit der Probenahme bei einem konstanten Wert p = 23 :P (→ y|p )=p 2 ( 1 - p )=23 2(1-23 )≈0,148 Glaubwürdigkeit der Stichprobe bei der Berechnung der Wahrscheinlichkeit der Rückzahlung des Kredits unter Berücksichtigung von Faktoren→x :P(→y|p)=3∏i=1pyi(1−p)(1−yi)=p11(1−p1)1−1⋅p12(1−p2)1−1⋅p03(1−p3)1−0==p 1 ≤ p 2 ≤ ( 1 - p 3 )=0,99 ⋅ 0,73 ⋅ ( 1 - 0,45 )≈0,397 Die Wahrscheinlichkeit einer Stichprobe mit einer Wahrscheinlichkeit, die in Abhängigkeit von Faktoren berechnet wurde, erwies sich als höher als die Wahrscheinlichkeit mit einem konstanten Wahrscheinlichkeitswert. Worüber spricht das? Dies deutet darauf hin, dass die Kenntnis der Faktoren es ermöglichte, die Wahrscheinlichkeit der Rückzahlung eines Kredits für jeden Kunden genauer auszuwählen. Daher ist es bei der Ausgabe eines anderen Kredits richtiger, das am Ende des dritten Abschnitts des Artikels vorgeschlagene Modell zur Abschätzung der Wahrscheinlichkeit der Rückzahlung von Schulden zu verwenden. Aber dann, wenn wirdie Wahrscheinlichkeitsfunktion der Stichprobemaximieren müssenVerwenden Sie dann einen Algorithmus, mit dem die Wahrscheinlichkeiten für Vasya, Fedi und Lesha beispielsweise 0,99, 0,99 bzw. 0,01 betragen. Vielleicht zeigt sich ein solcher Algorithmus in der Trainingsstichprobe gut, da er den Wert der Wahrscheinlichkeit der Stichprobe näher bringt1 , aber erstens wird ein solcher Algorithmus höchstwahrscheinlich Schwierigkeiten mit der Verallgemeinerungsfähigkeit haben, und zweitens wird dieser Algorithmus definitiv nicht linear sein. Und wenn Methoden zur Umschulung (ebenso schwache Verallgemeinerungsfähigkeit) eindeutig nicht im Plan dieses Artikels enthalten sind, gehen wir den zweiten Absatz genauer durch. Beantworten Sie dazu einfach eine einfache Frage. Kann die Wahrscheinlichkeit der Rückzahlung eines Kredits an Vasya und Feday unter Berücksichtigung der uns bekannten Faktoren gleich sein? Aus der Sicht der Soundlogik natürlich nicht, kann es nicht. Also, Vasya wird 2,5% seines Gehalts pro Monat geben, um das Darlehen zurückzuzahlen, und Fedya - fast 27,8%. Auch in Grafik 2 „Klassifizierung der Kunden“ sehen wir, dass Vasya viel weiter von der Trennlinie der Klassen entfernt ist als Fedya. Und schließlich wissen wir, dass die Funktionf(w,x)=w0+w1x1+w2x2 : 4.24 1.0 . , , , . , .
w , , ,
w , ,
Wurde w nach allen Regeln durchgeführt, so gehen wir davon aus - unsere Koeffizienten erlauben es uns, die Wahrscheinlichkeit besser einzuschätzen :)Wir waren jedoch abgelenkt. In diesem Abschnitt müssen wir verstehen, wie der Vektor der Gewichte bestimmt wird→ w , die erforderlich ist, um die Wahrscheinlichkeit der Rückzahlung eines Kredits durch jeden Kreditnehmer zu beurteilen. Fassen Sie kurz zusammen, nach welchem Arsenal wir Ausschau haltenw :
1. Wir gehen davon aus, dass der Zusammenhang zwischen der Zielgröße (Prognosewert) und dem das Ergebnis beeinflussenden Faktor linear ist. Aus diesem Grund wird die lineare Regressionsfunktion des Formulars verwendet.f ( w , x ) = → w T X , dessen Zeile Objekte (Clients) in Klassen unterteilt+ 1 und
- 1 oder
0 (Kunden, die das Darlehen zurückzahlen können und nicht können). In unserem Fall hat die Gleichung die Formf ( w , x ) = w 0 + w 1 × 1 + w 2 × 2 .
2. Wir verwenden die inverse Protokolltransformationsfunktion des Formularsp + = 11 + e - → w T → x =σ( → w T → x )für die Wahrscheinlichkeit des Objekts bestimmtzu der Klasse gehört+ 1 .
3. Wir betrachten unsere Trainingsstichprobe als Implementierung eines verallgemeinerten Bernoulli-Schemas , dh für jedes Objekt wird eine Zufallsvariable erzeugt, die mit hoher Wahrscheinlichkeit istp (sein eigenes für jedes Objekt) nimmt den Wert 1 und mit Wahrscheinlichkeit an( 1 - p ) - 0.4. Wir wissen, dass wirdie Wahrscheinlichkeitsfunktion der Stichprobeunter Berücksichtigung der akzeptierten Faktorenmaximieren müssen, damit die vorhandene Stichprobe die wahrscheinlichste wird. Mit anderen Worten, wir müssen solche Parameter auswählen, bei denen die Stichprobe am plausibelsten ist. In unserem Fall ist der ausgewählte Parameter die Wahrscheinlichkeit der Rückzahlung des Darlehensp , was wiederum von unbekannten Koeffizienten abhängtw .
Wir müssen also einen solchen Vektor von Gewichten finden → w , bei dem die Wahrscheinlichkeit der Probenahme maximal ist. 5. Wir wissen, dassSiedie Maximum-Likelihood-Methode verwendenkönnen, umdie Likelihood-Funktion einer Stichprobezu maximieren. Und wir kennen alle Tricks, um mit dieser Methode zu arbeiten. Hier ist ein solcher Mehrweg :)Und jetzt erinnern wir uns, dass wir am Anfang des Artikels zwei Arten der Verlustfunktion fürlogistischeVerluste ableiten wollten, je nachdem, wie die Klassen von Objekten bezeichnet werden. Es ist vorgekommen, dass bei Klassifizierungsproblemen mit zwei Klassen Klassen als bezeichnet werden+ 1 und
0 oder
- 1 .
Je nach Bezeichnung hat der Ausgang eine entsprechende Verlustfunktion.Fall 1. Einteilung von Objekten in + 1 und 0
Früher bei der Bestimmung der Wahrscheinlichkeit einer Stichprobe, in der die Wahrscheinlichkeit der Rückzahlung von Schulden durch den Kreditnehmer auf der Grundlage von Faktoren und festgelegten Koeffizienten berechnet wurde w , wir haben die Formel angewendet:P (→ y|p ) = 3 Π i = 1 p y i ( 1 - p ) ( 1 - y i )Tatsächlich
p i ist der Wertder logistischen Antwortfunktion p + = 11 + e - → w T → x =σ( → w T → x )für einen gegebenen Vektor von Gewichten→ w Dann hindert uns nichts daran, die Wahrscheinlichkeitsfunktion des Samples so zu schreiben:P (→ y|σ ( → w T X ) )=n Π i = 1 σ( → w T → x i ) y i( 1 - & sgr; ( → w T → x i ) ( 1 - y i )→m a x
Es kommt vor, dass es für einige unerfahrene Analysten manchmal schwierig ist, sofort zu verstehen, wie diese Funktion funktioniert. Schauen wir uns 4 kurze Beispiele an, die alles verdeutlichen:1. Wenny i = + 1 (d. h. gemäß der Trainingsstichprobe gehört das Objekt zur Klasse +1) und unser Algorithmusσ ( → w T X ) ) bestimmt die Wahrscheinlichkeit, ein Objekt zu klassifizieren+ 1 gleich 0,9, dann wird diese Stichprobenwahrscheinlichkeit wie folgt berechnet:0,9 1 ≤ ( 1 - 0,9 ) ( 1 - 1 ) = 0,9 1 ≤ 0,1 0 = 0,9 2.Wenny i = + 1 undσ ( → w T X ) ) = 0,1 , dann lautet die Berechnung wie folgt:0,1 1 ≤ ( 1 - 0,1 ) ( 1 - 1 ) = 0,1 1 ≤ 0,9 0 = 0,1 3.Wenny i = 0 undσ ( → w T X ) ) = 0,1 , dann lautet die Berechnung wie folgt:0,1 0 ≤ ( 1 - 0,1 ) ( 1 - 0 ) = 0,1 0 ≤ 0,9 1 = 0,9 4.Wenny i = 0 undσ ( → w T X ) ) = 0,9 , dann lautet die Berechnung wie folgt:0,9 0 ≤ ( 1 - 0,9 ) ( 1 - 0 ) = 0,9 0 ≤ 0,1 1 = 0,1 Es ist offensichtlich, dass die Wahrscheinlichkeitsfunktion in den Fällen 1 und 3 oder im allgemeinen Fall mit korrekt erratenen Werten der Wahrscheinlichkeiten der Klassifizierung eines Objekts als Klasse maximiert wird+ 1 .
Aufgrund der Tatsache, dass bei der Bestimmung der Wahrscheinlichkeit der Klassifizierung eines Objekts als Klasse + 1 Wir kennen nicht nur die Koeffizientenw , dann werden wir sie suchen. Wie oben erwähnt, ist dies ein Optimierungsproblem, bei dem wir zuerst die Ableitung der Wahrscheinlichkeitsfunktion in Bezug auf den Gewichtsvektor finden müssenw .
Es ist jedoch sinnvoll, die Aufgabe zunächst zu vereinfachen: Wir werden die Ableitung des Logarithmus der Wahrscheinlichkeitsfunktion suchen .L l o g ( X , → y , → w ) = n Σ i = 1 ( - y il o g eσ ( → w T → x i ) - ( 1 - y i )l o g e( 1 - σ ( → w T → x i ) ) ) → m i n
Warum haben wir nach dem Logarithmus in der Funktion des logistischen Fehlers das Vorzeichen mit geändert?+ auf
- .
Alles ist einfach, da es bei Problemen der Modellqualitätsbewertung üblich ist, den Wert einer Funktion zu minimieren, haben wir die rechte Seite des Ausdrucks mit multipliziert - und statt zu maximieren, minimieren wir jetzt die Funktion. Tatsächlich wurde jetzt vor Ihren Augen die Verlustfunktion - derlogistische Verlustfür das Training mit zwei Klassen- sehr gelitten.+ 1 und
0 .
Um die Koeffizienten zu finden, müssen wir nur die Ableitung der logistischen Fehlerfunktion finden und dann unter Verwendung numerischer Optimierungsmethoden wie Gradientenabstieg oder stochastischer Gradientenabstieg die optimalsten Koeffizienten auswählenw .
In Anbetracht der ohnehin geringen Größe des Artikels wird jedoch vorgeschlagen, unabhängig voneinander zu differenzieren, oder dies wird möglicherweise das Thema für den nächsten Artikel mit viel Arithmetik ohne solche detaillierten Beispiele sein.Fall 2. Einteilung von Objekten in + 1 und −1
,
1 und
0 ,
Logistic Loss , . .
«..., ...» . ,
i -
+1 ,
p ,
−1 ,
(1−p) . :
P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)[yi=+1](1−σ(→wT→xi)[yi=−1])→max
. 4 :
1. yi=+1 und
σ(→wT→xi)=0.9 , «»
0.92. yi=+1 und
σ(→wT→xi)=0.1 , «»
0.13. yi=−1 und
σ(→wT→xi)=0.1 , «»
1−0.1=0.94. yi=−1 und
σ(→wT→xi)=0.9 , «»
1−0.9=0.1, 1 3 , ,
, . , . , , .
Llog(X,→y,→w)=n∑i=1(−[yi=+1]logeσ(→wT→xi)−[yi=−1]loge(1−σ(→wT→xi)))→min
σ(→wT→xi) 11+e−→wT→xi :
Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(1−11+e−→wT→xi))→min
, :
Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(11+e→wT→xi))→min
«..., ...» . ,
yi +1 , , ,
e −→wT→xi ,
−1 , $e$
+→wT→xi . — :
−yi→wT→xi .
:
Llog(X,→y,→w)=n∑i=1−loge(11+e−yi→wT→xi)→min
, "
− " () , :
Llog(X,→y,→w)=n∑i=1loge(1+e−yi→wT→xi)→min
logistic Loss , :
+1 und
−1 .
, .
← — « »Unterstützende Materialien
1.
1) / . , . – 2- . – .: , 1986 ( )
2) / .. — 9- . — .: , 2003
3) / .. — : , 2007
4) -: / . ., . . — 2- . — -: , 2013
5) Data Science / — -: , 2017
6) Data Science / ., . — -: , 2018
2. , ()
1)
,2)
,3)
. ODS, Yury Kashnitsky4)
4, ( 47 )5)
,3. -
1)
2)
3)
4)
5)
6)
7)
8)
e ?9)