Las barras de Zhenya y Luke: una herramienta multiplicadora de finales del siglo XIX
Este artículo está dedicado a una herramienta auxiliar para la multiplicación, barras propuestas en 1885 por el ingeniero ferroviario Eugene (sic) y un empleado del Museo de Artes y Oficios de París Eduard Luke (sic) [1].La transliteración de los nombres de los inventores difiere en diferentes fuentes, por lo que cito en latín una serie de opciones (que tuve que buscar en google): Genaille (Zhenya, Zhenya, Zhenya, Zhenail), Lucas (Luca, Luc, Lucas).Las barras de Zhenya y Luke eran más convenientes que las varitas de Neper que las precedieron, y bien podrían competir con las barras modernas de Joffe (basadas en el teorema de Slonimsky).Prácticamente no hay información sobre este producto en Runet. El otro día, de repente busqué en Google un artículo en alemán que me ayudó a entrar en el principio de los bares. Sin limitarme al artículo, restauré la apariencia de la superficie de trabajo de las barras de las imágenes con una vista de algunas de ellas y centrándome en el principio de su acción. Los materiales encontrados más tarde en el mismo sitio confirmaron la exactitud de mi reconstrucción.Propósito de escribir un artículo
Este artículo es para aquellos que, como yo, están interesados en la historia de la tecnología informática.En RuNet, no pude encontrar nada sensato sobre los bares de Zhenai y Luc (Genaille y Lucas). El sitio web en idioma alemán , en el que se encontró un artículo con su descripción, ayudó a comprender el principio de funcionamiento de esta herramienta de conteo .Por qué se selecciona a Habr como ubicación del artículo
El artículo está dedicado, aunque antiguo, pero sigue siendo tecnología informática. Por lo tanto, es adecuado para Habr sobre un tema.Habr está bien indexado, y quiero que sea fácil para cualquiera que esté interesado en esta herramienta de conteo encontrar información sobre ella.Descripción del producto y función
Las barras de Zhenya y Luke, así como otros productos similares, están diseñados para obtener rápidamente el producto de un número de varios dígitos con un número de un solo dígito.La herramienta de multiplicación es un conjunto de 11 barras. Cada barra tiene una escala digital en la que se encuentra el resultado. La escala se divide en 8 partes, que corresponden a la multiplicación por números del 2 al 9. Una barra sirve como pista: las partes de su escala están firmadas por los números 2 ... 9: estos son los valores de un factor de un solo dígito, y su escala está diseñada para leer el nivel más alto del trabajo. Las barras restantes están numeradas del 0 al 9 y están diseñadas para multiplicar los números correspondientes. En ellos, al lado de la escala, hay un triángulo, cuyo lado derecho limita la escala digital a la izquierda, y el vértice izquierdo está en el borde izquierdo de la barra: cuando las barras se apilan juntas, indica la posición de la próxima descarga del producto en la barra siguiente.
Un pequeño análisis: es fácil ver que cada parte de la escala de cada barra comienza con un dígito igual al valor de la categoría de unidades del producto del número de la barra por el número de parte de la escala. Por ejemplo, en la barra 8, el fragmento 9 comienza con el número 2 (8 * 9 = 72). La longitud de cada parte de la escala es igual al valor de un factor de un solo dígito, lo cual es natural, porque al multiplicar cualquier número por un factor de un solo dígito, el dígito más alto del producto es menor que este factor, es decir cuando se multiplica, por ejemplo, por 5, el valor transferido al siguiente dígito nunca excederá de 4, cuando se multiplica por 9, respectivamente, 8, etc. La cantidad de desplazamiento de dígitos hacia abajo desde el comienzo de la escala es igual al valor de la transferencia desde el bit menos significativo. Resulta que la posición del vértice izquierdo del triángulo negro corresponde al valor del segundo bit del producto del número de barra por un factor de un solo dígito, al que se agrega un número,transferido desde el orden inferior.Para multiplicar un número de varios dígitos por un número de un solo dígito, debe agregar las barras junto con los números correspondientes a los dígitos de los dígitos y adjuntar una barra con una pista a la izquierda. Luego, en cada parte de la escala, será posible considerar los productos de este número por el número de un solo dígito correspondiente. La descarga de unidades es el primer dígito de la parte deseada de la escala, y cada descarga posterior nos indicará el vértice izquierdo del triángulo, cuyo lado derecho sirve como el borde izquierdo de la celda de la descarga anterior.Por ejemplo, tome el número 7519. Armemos una barra con una pista y las barras 7, 5, 1 y 9. El diagrama se muestra en la imagen a continuación.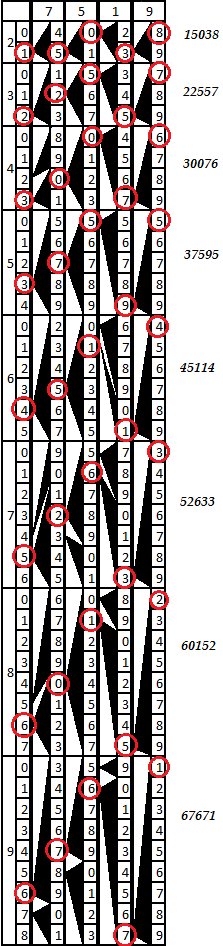
En cada parte de la tabla resultante, siguiendo los signos de triángulo, puede trazar las categorías de obras de derecha a izquierda.El esquema es más claro que cualquier palabra. Sigamos, por ejemplo, la multiplicación por 9. Al comienzo de la novena (última) parte de la escala de la barra derecha vemos el número 1. El triángulo de allí indica el número 7 de la barra vecina, desde allí el triángulo indica 6, luego - 7, y aún más - el número 6 en la escala de la punta de la barra. A. obtenemos el valor 67671 = 7519 * 9.También se trazan otras obras. Es fácil verificar que sean correctos. Por lo tanto, la herramienta es adecuada para su uso.Especulaciones sobre el tema de la apariencia.
Apokin I.A., Maistrov L.E. en la fuente [1] escriben que las barras digitales tenían las cuatro superficies funcionando. Es lógico suponer que las superficies se usaron para duplicar escalas, lo cual es necesario para compilar números de varios dígitos con varias ocurrencias del mismo dígito.Según el número de lados de la barra, supongamos que hay cuatro juegos completos de escalas en 10 barras.Suponga que las escalas en las barras deben estar dispuestas de modo que las barras le permitan hacer cualquier número de cuatro dígitos.Puede encontrar muchas opciones para colocar escalas de trabajo en barras que satisfacen este requisito. Por ejemplo, tome dos barras de cinco tipos con caras, respectivamente:0,1,2,3;2,3,4,5;4,5,6,7;6,7,8,9;0,1,8,9.Otra opción para usar cuatro caras es colocar una escala en ellas en partes y así reducir la longitud de la barra. Esta opción es menos conveniente de usar, porque no permite ver todas las obras a la vez.La escala consta de 8 partes, que varían en longitud de 2 a 9. Colecciónalos en cuatro grupos sin alterar el orden:2 + 3 + 4 + 5 = 14; 6 + 7 = 13; 8; 9. La longitud más larga es 14.Si está permitido alterar el orden, entonces las partes de la escala se agrupan fácilmente:2 + 9; 3 + 8; 4 + 7; 6 + 5. Aquellos. La longitud de la barra se reduce a 11.Literatura
1. Apokin I.A., Maistrov L.E. "La historia de la tecnología informática: desde los dispositivos informáticos más simples hasta los complejos sistemas de retransmisión". (Moscú: Nauka Publishing House, 1990)2. www.mechrech.infoPD
Una pregunta para aquellos que saben francés: ¿cómo diablos es correcto traducir los nombres de Genaille y Lucas correctamente?UPD: gracias. Corregido en todo el artículo sobre Zhenai (clase) y Luke (no clase) Source: https://habr.com/ru/post/es380549/
All Articles