La "paradoja de la inspección" está en todas partes

Muchas personas conocen la llamada "paradoja de la amistad" en las redes sociales, mencionada por primera vez en el trabajo científico de 1991, cuando las redes sociales solo estaban fuera de línea. Esta paradoja se aplica a las redes sociales modernas en Internet.

Si toma un usuario de Facebook y selecciona al azar a cualquiera de sus amigos, entonces con una probabilidad del 80%, un amigo tendrá más "amigos". Las personas que son nuevas en las estadísticas matemáticas están muy molestas por el hecho de que casi todos los amigos tienen más "éxito" en la comunicación que ellos mismos. Pero no hay razón para la depresión: debe ser así, de acuerdo con la ciencia y el sentido común.

La paradoja de la amistad es una de las formas de la "paradoja de la inspección", que se encuentra en todas partes y a menudo engaña a la gente del pueblo.

La esencia de la paradoja de la amistad es que los usuarios con una gran cantidad de amigos tienen más probabilidades de caer en la muestra estadística. Por ejemplo, de acuerdo con la Colección de datos de la red de Stanford , el usuario promedio de Facebook tiene 42 amigos en una muestra de 4,000 personas, y cada uno de estos amigos tiene un promedio de 91 amigos.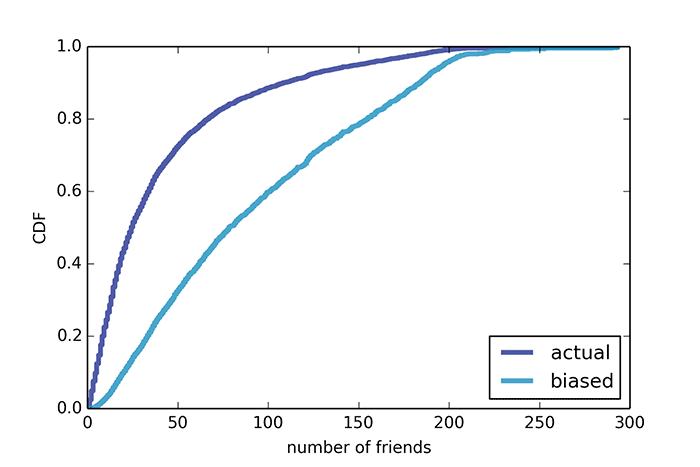



Lo mismo se observa en otras áreas de investigación.

Por ejemplo, la paradoja del tamaño de la clase. Supongamos que entrevistamos a los estudiantes cuántas personas estudian con ellos en un grupo, y luego derivamos la media aritmética de sus respuestas, y obtenemos 56 personas. Pero la administración de la universidad dice que el número promedio de estudiantes en un grupo es 31. Por extraño que parezca, nadie miente, y ambos valores son justos. Solo durante la encuesta, los estudiantes de grupos grandes tienen más probabilidades de ingresar a la muestra, porque en realidad hay más de ellos. Si tenemos dos grupos de 10 y 100 personas, entonces 100 de los 110 encuestados nombrarán el tamaño de su grupo a 100 personas, y solo 10 personas nombrarán el tamaño del grupo 10. El tamaño promedio del grupo, según esta encuesta, será de 92 estudiantes.

Parecería un error común, pero es una fuente de malentendidos en muchas situaciones reales. Por ejemplo, al analizar el tráfico de pasajeros en el transporte público. Un profesor de ciencias de la computación, Allen Downey, para un artículo en el Journal of the American Statistical Society ofrece un ejemplo del tiempo promedio entre los trenes de la Línea Roja en Boston. Grabó la hora de llegada de 70 trenes entre las 17:00 y las 18:00.



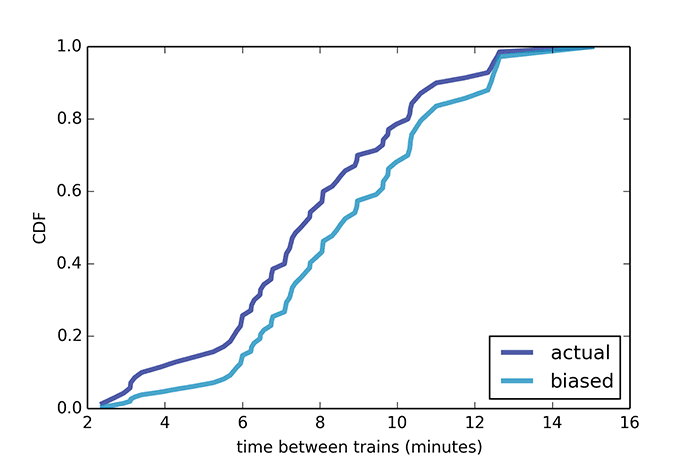El intervalo mínimo entre trenes fue de 3 minutos, el máximo: 15 minutos. Según los datos reales, el intervalo promedio entre trenes es de 7.8 minutos, es decir, el tiempo de espera promedio para un tren debe ser de aproximadamente 3.9 minutos. Pero una encuesta de pasajeros muestra que el tiempo de espera promedio fue en realidad 4,4 minutos, y el intervalo entre trenes fue de 8,8 minutos, es decir, un 15% más.

La razón es que con una mayor demora en el tren, más pasajeros lo esperan, mientras que los trenes que llegan con un intervalo más corto se llenan menos. En consecuencia, la mayoría de los pasajeros se quejan del aplastamiento en el automóvil y del largo tiempo de espera del tren, mientras que, según la compañía, el tiempo promedio y la carga de los automóviles es normal.

El mismo problema con los vuelos. La mayoría de los pasajeros hablan de salones de cabina completa, mientras que las aerolíneas se quejan de la pérdida de ganancias porque muchos vuelos vuelan casi vacíos. Ambos tienen razón.

La "paradoja de la inspección" se observa, por ejemplo, en carreras de larga distancia o cuando se viaja en automóvil por la carretera. En cada uno de estos casos, el participante en el movimiento supera "demasiado lento", y lo supera "demasiado rápido". Crea una impresión subjetiva de que todos los participantes en el movimiento se dividen en demasiado lento o demasiado rápido, pero no en el promedio.

El último ejemplo de Allen Downey nació después de leer Orange - The Hit of the Season, una memoria de Piper Kerman, quien pasó 13 meses en una prisión federal. En uno de los fragmentos del libro, expresa sorpresa por la larga duración de las oraciones que los presos están cumpliendo. Obviamente, la niña no está familiarizada con las leyes de la estadística matemática. Pero de acuerdo con la paradoja de la inspección, si vas a la cárcel en un momento aleatorio y eliges a un prisionero al azar, entonces con un alto grado de probabilidad es sentenciado a una larga pena de prisión. Esto no es evidencia del inhumano sistema penitenciario de los Estados Unidos, sino una simple conclusión de la paradoja de la inspección.



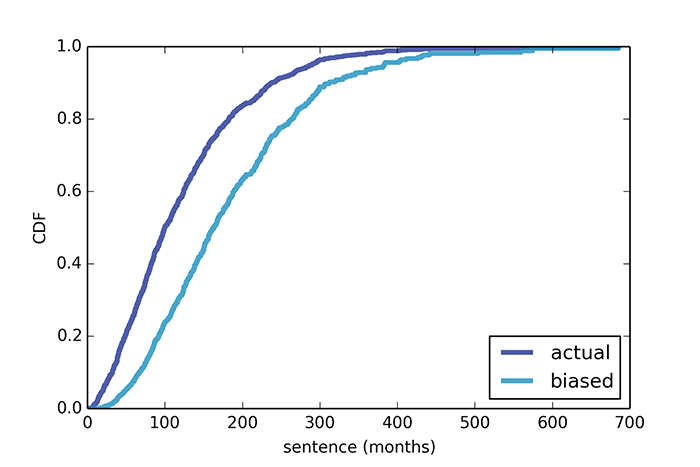Según datos oficiales de la Comisión de Sentencias de los Estados Unidos, el término promedio es de 121 meses, y el "término promedio subjetivo" para entrevistar a prisioneros es de 183 meses.

Incluso cuando se entrevista a prisioneros cercanos durante trece meses, como muestra el cálculo, el resultado promedio obtenido no difiere mucho de la encuesta inicial única.



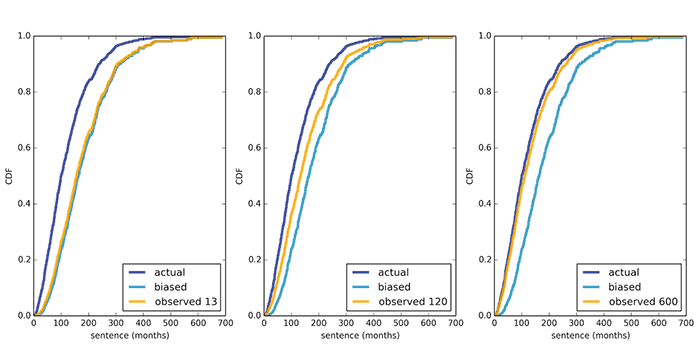Se puede obtener una cifra más o menos objetiva entrevistando durante 600 meses o más.

Source: https://habr.com/ru/post/es383787/