Algunos sensores de aceleración requieren calibración cero adicional después del montaje en la placa. Cuando vi varias fuentes con la calibración de sensores de aceleración, donde el componente G se tuvo en cuenta simplemente restando el valor = 9.8 m / s2 del eje Z, surgió la idea de escribir esta nota.
Estructura de publicación
- Problema
- Declaración del problema y método de solución.
- ¿Cómo conseguir los puntos?
- ¿Cómo calcular el centro de la pelota?
- ¿Cómo acelerar la búsqueda del centro de la pelota?
- ¿De qué otra manera acelerar la búsqueda del centro de la pelota?
- Sobre errores de medición
- Total
Problema
¿Cuál es el problema? Los sensores MEMS después de la instalación en la placa sufren deformaciones menores que afectan:- posición cero;
- escala de valores medidos;
- La perpendicularidad de los ejes entre sí.
Y si la escala y la perpendicularidad se violan no tan notablemente, entonces la posición de cero se enreda de manera tangible. Por ejemplo, si traduce el valor típico del desplazamiento cero para el acelerómetro del sensor MPU9250 a m / s 2 , entonces esto se obtiene en la región de 0.2 m / s 2 . Es decir, el sensor está parado, pero muestra aceleración, y después de 5 segundos obtenemos una velocidad de 1 m / s. Por un lado, todos los datos del sensor siempre se pasan a través de algún tipo de filtro (por ejemplo, tal ). Pero, por otro lado, ¿por qué el filtro debe compensar constantemente este sesgo? Después de todo, el sensor mostrará movimiento donde no está. Esto reduce la precisión del resultado. Con todo, necesita encontrar el valor de compensación una vez y luego restar este valor de sus lecturas durante la operación del sensor.La solución más simple para encontrar el valor de la compensación de cero, que viene inmediatamente a la mente, es crear las condiciones bajo las cuales el sensor debe mostrar cero con precisión. ¡El valor registrado en el sensor es el valor del desplazamiento cero! ¿Entonces? Pero no, la gravedad está actuando constantemente sobre el acelerómetro. Para evitarlo, se necesitará ingravidez (lanzar no funcionará). El campo magnético de la Tierra actúa en la brújula y su rotación en el giroscopio. Entonces, si no tienes una nave espacial personal, tendrás que encontrar algo.La segunda solución que viene a la mente de inmediato es colocar el sensor (o más bien su eje) en una posición en la que sepamos exactamente qué debe mostrar el sensor. La diferencia entre lo que muestra el sensor y lo que debería mostrar, ¡y habrá un desplazamiento cero! ¿Entonces? Por ejemplo, sabemos que si el acelerómetro se coloca en un nivel con el horizonte, entonces, en teoría, el vector de aceleración gravitacional se dirigirá exactamente a lo largo del eje Z del sensor. La magnitud del vector de aceleración que conocemos.Sin embargo, hay un problema. Consiste en el hecho de que no podemos establecer con precisión el eje del sensor a un nivel con el horizonte. El hecho es que la superficie en la que confiaremos no es paralela a la placa de circuito impreso. Eso, a su vez, no es paralelo al sitio en el que se encuentra el sensor. El sensor en sí no se encuentra exactamente en su sitio y los ejes dentro del sensor no son paralelos al cuerpo del sensor. El error al establecer el eje en relación con el horizonte en 1 grado da una proyección de tamaño comparable al valor del desplazamiento cero en sí, que queremos encontrar. En el caso de un magnetómetro, tampoco sabemos a dónde se dirige el vector de campo magnético. En teoría, hacia el norte. Pero en la práctica, el campo magnético de la Tierra en sí es heterogéneo en intensidad y dirección. Además, los objetos metálicos cercanos hacen sus ajustes.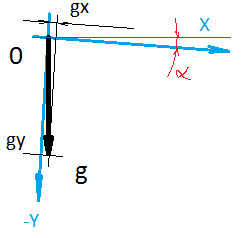
Declaración del problema y método de solución.
La tarea es la siguiente: necesitamos determinar el vector de desplazamiento cero usando las lecturas del sensor, que siempre registrarán el vector de desplazamiento + vector de influencia externa constante (aceleración gravitacional, rotación de la Tierra, campo magnético de la Tierra), la magnitud y dirección de la cual no sabemos (en el caso del acelerómetro conocemos el valor, pero nuevamente la escala del sensor puede no ser igual a 1).La forma de resolver. Este artículo propone determinar el vector de desplazamiento de la siguiente manera. Tomamos y giramos el sensor en todos los sentidos y registramos las lecturas del sensor. Después de N mediciones, los valores tomados del sensor y ubicados en el gráfico serán una bola, cuyo radio es la magnitud del impacto externo, y el centro es el desplazamiento cero exacto deseado.¿Cómo conseguir los puntos?
Para facilitar el procedimiento de medición en sí, puede escribir un programa simple. Debe registrar los sensores cuando el dispositivo está parado. Solo necesitamos girar el dispositivo a la posición deseada. Para determinar un estado estacionario, también es adecuado un acelerómetro no calibrado: simplemente tome la diferencia entre el valor actual y el anterior. Y si hay más ruido, entonces arreglamos el movimiento. Mi umbral se obtiene en la región de 0.07G. Si lo sostiene con las manos, resultará más de este valor. Utilicé cinta adhesiva para fijar la posición. Si todavía no funciona, verifique si hay un refrigerador, un ventilador o algo similar cerca.¿Cómo puede estar en código?
static TSumSensorsData g_sens_data[2];
static int32_t g_sens_data_sum_cnt[2];
static uint8_t g_sens_data_num;
IS_INTERRUPT void on_dma_raw_ready_calibrate_step1()
{
SensorRawBuffer *raw = sensor_get_raw_buffer();
g_sens_data[g_sens_data_num].acc_x += swap_i16(raw->accell_x_unswap);
g_sens_data[g_sens_data_num].acc_y += swap_i16(raw->accell_y_unswap);
g_sens_data[g_sens_data_num].acc_z += swap_i16(raw->accell_z_unswap);
g_sens_data[g_sens_data_num].gyro_x += swap_i16(raw->gyro_x_unswap);
g_sens_data[g_sens_data_num].gyro_y += swap_i16(raw->gyro_y_unswap);
g_sens_data[g_sens_data_num].gyro_z += swap_i16(raw->gyro_z_unswap);
g_sens_data[g_sens_data_num].mag_x += raw->mag_x_raw * g_mag_calibrate.kx;
g_sens_data[g_sens_data_num].mag_y += raw->mag_y_raw * g_mag_calibrate.ky;
g_sens_data[g_sens_data_num].mag_z += raw->mag_z_raw * g_mag_calibrate.kz;
g_sens_data_sum_cnt[g_sens_data_num]++;
}
void sensors_calibrate_program(FlashROM *flash_ptr)
{
double calibrate_result_error[3];
TVector16 calibrate_result[3];
int32_t radius[ACCEL_NO_MOTION_DETECT_COUNT];
uint8_t raw_is_deleted[ACCEL_NO_MOTION_DETECT_COUNT];
TVector16 raw[3][ACCEL_NO_MOTION_DETECT_COUNT];
. . .
g_sens_data_sum_cnt[0] = 0;
g_sens_data_num = 0;
int16_t prev_avg_x = 0;
int16_t prev_avg_y = 0;
int16_t prev_avg_z = 0;
int8_t low_motion_cnt = 0;
while(low_motion_cnt < ACCEL_NO_MOTION_DETECT_COUNT)
{
if (g_sens_data_sum_cnt[g_sens_data_num] >= ACCEL_NO_MOTION_DETECT_SAMPLES)
{
uint8_t new_data_num = (g_sens_data_num + 1) & 1;
g_sens_data[new_data_num].acc_x = 0;
g_sens_data[new_data_num].acc_y = 0;
g_sens_data[new_data_num].acc_z = 0;
g_sens_data[new_data_num].gyro_x = 0;
g_sens_data[new_data_num].gyro_y = 0;
g_sens_data[new_data_num].gyro_z = 0;
g_sens_data[new_data_num].mag_x = 0;
g_sens_data[new_data_num].mag_y = 0;
g_sens_data[new_data_num].mag_z = 0;
g_sens_data_sum_cnt[new_data_num] = 0;
uint8_t old_data_num = g_sens_data_num;
g_sens_data_num = new_data_num;
int16_t avg_x = g_sens_data[old_data_num].acc_x / g_sens_data_sum_cnt[old_data_num];
int16_t avg_y = g_sens_data[old_data_num].acc_y / g_sens_data_sum_cnt[old_data_num];
int16_t avg_z = g_sens_data[old_data_num].acc_z / g_sens_data_sum_cnt[old_data_num];
int16_t dx = avg_x - prev_avg_x;
int16_t dy = avg_y - prev_avg_y;
int16_t dz = avg_z - prev_avg_z;
prev_avg_x = avg_x;
prev_avg_y = avg_y;
prev_avg_z = avg_z;
if ((abs_i16(dx) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dy) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dz) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE))
{
raw[RAW_ACC][low_motion_cnt].x = avg_x;
raw[RAW_ACC][low_motion_cnt].y = avg_y;
raw[RAW_ACC][low_motion_cnt].z = avg_z;
raw[RAW_GYRO][low_motion_cnt].x = g_sens_data[old_data_num].gyro_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].y = g_sens_data[old_data_num].gyro_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].z = g_sens_data[old_data_num].gyro_z / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].x = g_sens_data[old_data_num].mag_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].y = g_sens_data[old_data_num].mag_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].z = g_sens_data[old_data_num].mag_z / g_sens_data_sum_cnt[old_data_num];
low_motion_cnt++;
beep();
delay_ms(2000);
}
}
}
. . .
}
Para obtener la bola en el gráfico, debe girar el dispositivo con el sensor de acuerdo con un determinado esquema. Para estos fines, el globo es muy adecuado, ya que tiene un marcado. Puede pensar que necesita esculpir en todo el mundo. Pero esto no es así.Ejemplo de resultado incorrecto Es necesario esculpir el sensor no en toda la superficie del globo, sino en un meridiano. Supongamos que tomamos siete puntos en el meridiano (el primero y el último en los polos norte y sur). En cada punto del meridiano, conectamos su dispositivo al globo y aún giramos el dispositivo alrededor de su eje con un cierto paso, por ejemplo, 30-35 grados. Resulta que si gira 12 veces alrededor de su eje, en 7 puntos en total se obtienen 84 mediciones.
La belleza del método es que todo se puede hacer "en la rodilla". La precisión de posicionamiento no juega un papel especial, solo necesita girar de acuerdo con el esquema para que el vector de influencia externa en el gráfico atraiga una bola. El correcto se parece a esto: vea la figura (el centro está marcado con una marca).
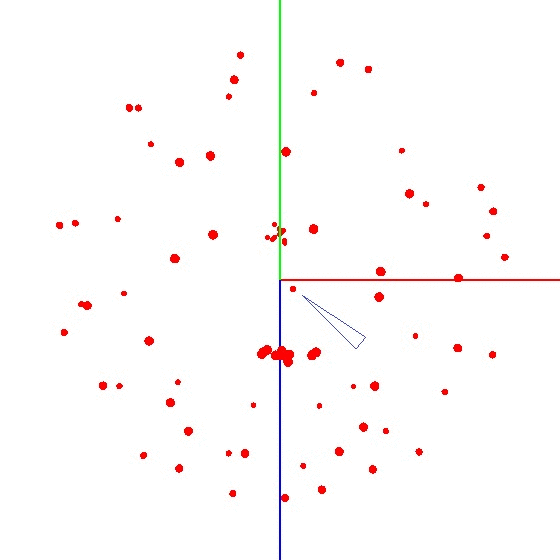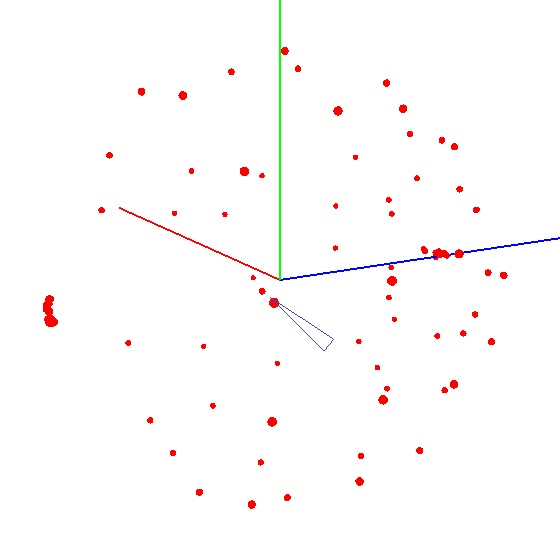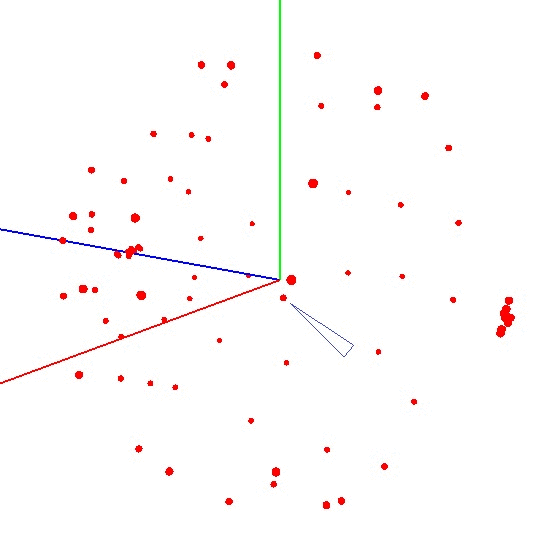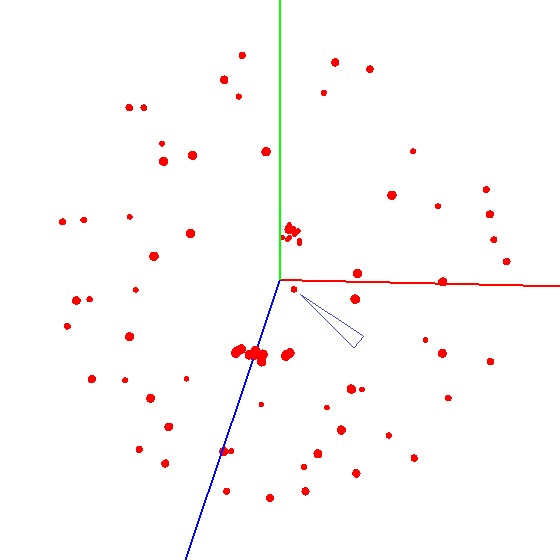
¿Cómo calcular el centro de la pelota?
Esta es una tarea interesante y tiene varias soluciones. Puede parecer que para buscar el centro, es suficiente tomar el promedio aritmético de las coordenadas de los puntos obtenidos. Sin embargo, esto no es así: los puntos se pueden ubicar de manera desigual en la pelota (ver. Fig.).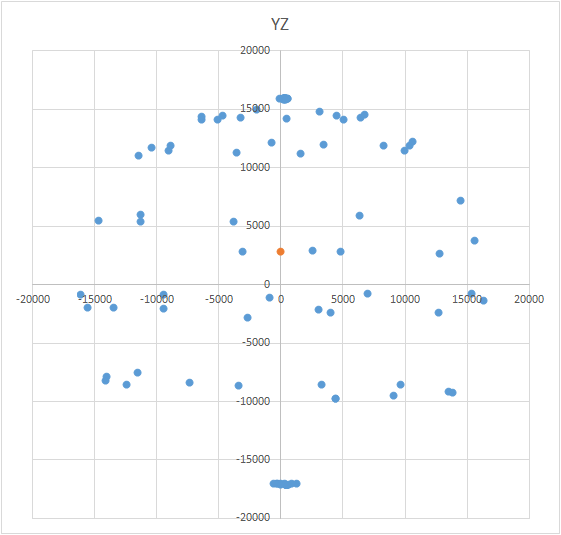
La ecuación de la pelota se ve así: (X - A) 2 + (Y - B) 2 + (Z - C) 2 = R 2 , donde X, Y, Z son las coordenadas del punto que se encuentra en la pelota. A, B, C son las coordenadas del centro en los ejes x, y y z, respectivamente. R es el radio de la pelota. Puede construir un sistema de ecuaciones e intentar resolver este sistema de manera más simple utilizando algún método. O simplemente puede buscar el centro (esto es como un método de aproximaciones sucesivas). El significado del método es simple: el valor de error (X - A) 2 + (Y - B) 2+ (Z - C) 2 - R 2 debe tender a cero. Esto significa que la suma de estas cantidades para todos los puntos de la esfera también debería tender a cero. Sabiendo esto, podemos elegir los valores A, B y C para los cuales el error para todos los puntos será mínimo. El área de búsqueda está limitada por el tamaño de la pelota (cubo condicional). Es decir, debemos colocar secuencialmente el centro de la pelota en todos los puntos del cubo y calcular el error. Donde hay un error mínimo, ahí está el centro.
Como R, necesitamos tomar el valor teórico del vector de influencia externa, para el acelerómetro, esta es la aceleración de la gravedad, para la brújula, esta es la magnitud promedio del campo magnético de la Tierra, para el giroscopio, la velocidad de rotación de la Tierra. Por supuesto, en la fórmula debe haber valores de una dimensión (unidades convencionales del sensor o m / s 2, grados / s, etc.). Es más conveniente convertir a unidades arbitrarias del sensor correspondiente.¿Cómo calcular un cierto valor en las unidades estándar del sensor?= * / ( — )
: 16- ±2g ?:
9,8 /2 * 65536 / (2g + 2g) = 9,8 /2 * 65536 / (2 * 9,8 /2 + 2 * 9,8 /2) = 16384 . . .
Por cierto, si conoce el radio de la pelota exactamente, entonces puede calcular el centro solo por su "cuña". Es decir, en puntos que se encuentran solo en un pedazo de la superficie de la pelota. Pero este no es nuestro caso.¿Cómo acelerar la búsqueda del centro de la pelota?
Es necesario buscar el centro no en todo el cubo (las dimensiones de la pelota), sino a lo largo de la línea, cuyo comienzo es arbitrario, cada punto siguiente está más cerca del centro real y el final está en el centro. Supongamos que comenzamos desde el punto (0; 0; 0) ... Siempre nos movemos con un paso constante. Por lo tanto, si imaginamos un conjunto de cubos de 3x3x3, donde cada cara es igual al tamaño del paso y también imaginamos que la posición actual es el cubo del medio, entonces tenemos 9 + 8 + 9 opciones donde colocar el siguiente punto. Solo tenemos que estar en cada punto, para calcular en cuál de los 26 puntos vecinos el error será menor. Si resulta que el error es menor en el punto actual, y no en uno de los vecinos, significa que está en el centro y la búsqueda ha terminado.
¿Cómo puede estar en código?Public Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai, B + bi, C + ci, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
Exit Do
End If
A = A + ai_min
B = B + bi_min
C = C + ci_min
Loop
. . .
¿De qué otra manera acelerar la búsqueda del centro de la pelota?
Necesita buscar con paso variable. Primero buscamos el centro en grandes pasos. Encontramos el centro, reducimos el paso y desde allí comenzamos a buscar más. Y así sucesivamente, hasta que obtenga el resultado de la precisión necesaria.¿Cómo puede estar en código?Public Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
step = 1000
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai * step, B + bi * step, C + ci * step, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
step = step / 10
If step < 0.01 Then
Exit Do
End If
Else
A = A + ai_min * step
B = B + bi_min * step
C = C + ci_min * step
End If
Loop
. . .
Sobre errores de medición
Durante las mediciones, puede haber situaciones en las que, por alguna razón, el resultado de la medición puede estar mucho más lejos de la superficie de la pelota. O podría ser muchos puntos. O, en general, el resultado de las mediciones puede no ser una pelota, sino un "huevo" o una "aeronave". En este caso, por supuesto, debe repetir todas las mediciones, identificando las posibles causas de errores. Por ejemplo, para un magnetómetro puede ser un perno o un clavo en una mesa y está tomando medidas directamente sobre él. Y cuanto más bajo baje el sensor a lo largo del meridiano, más fuerte será el metal afectará el resultado. Por lo tanto, es necesario determinar el umbral del valor de error permitido. Para no rehacer las mediciones debido a varios puntos claramente erróneos, puede aplicar un filtro. El principio del filtro es muy simple: después de calcular el centro por primera vez, clasifique los puntos por el nivel de error en cada uno de ellos.Algunos de los puntos con el mayor error simplemente se pueden descartar (por ejemplo, 10%). Luego debe repetir la búsqueda del centro.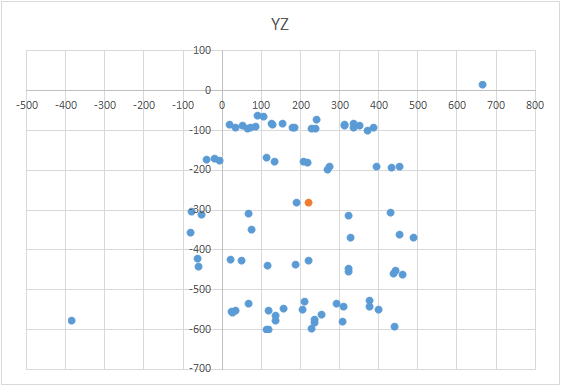
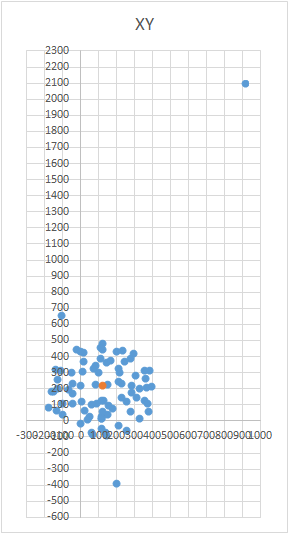
Total
El método tiene bastante buena precisión. El método le permite hacerlo con medios simples improvisados (pelota, banco, etc.). Funciona lo suficientemente rápido. Código simple Muchos sensores tienen registros especiales donde puede escribir el valor encontrado, y el sensor lo restará sobre la marcha. Dichos registros suelen tener el prefijo "TRIM", como en el MPU9260, o "OFFSET", como en el LSM303. Pero el conocido LIS302DL no tiene tales registros.No olvides poner un signo más si te gustó. Escriba en los comentarios sus métodos para calibrar sensores.