♋️ ⌚️ 🤘🏼 Luz comprimida o Qué tienen ondas gravitacionales ☄️ 🐉 🚻

Hola GT Hoy hablaremos sobre un estado de luz inusual y sus aplicaciones igualmente inusuales. Bienvenido a cat.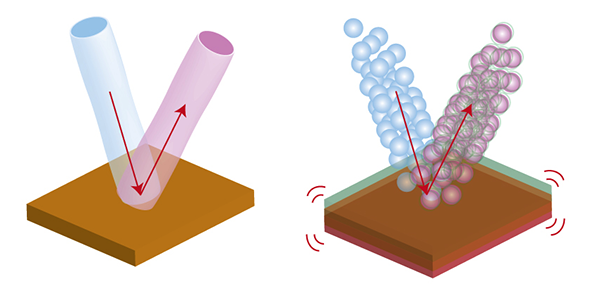

Un policía detiene a Heisenberg que ha excedido la velocidad.
"¿Sabes lo rápido que conduces?"
"No, pero sé exactamente dónde estaba".
(anécdota barbada)

La relación de incertidumbre de Heisenberg prohíbe medir simultáneamente la coordenada y la velocidad (momento) de una partícula. Además, nadie se molesta en medir con precisión una de las cantidades, pero la segunda incertidumbre será aún mayor.

En general, las relaciones de incertidumbre son bastante comunes en física. Por ejemplo, la misma relación es verdadera para una onda electromagnética: relaciona su intensidad (= número de fotones) y fase :

Debido a esta incertidumbre, no podemos medir con precisión la sinusoide descrita por la onda, para el observador siempre estará en turbidez acústica:

Esto se puede mostrar claramente en un gráfico circular, donde la amplitud corresponde al radio del punto, fase, el ángulo entre la dirección del punto y el eje X. El verde muestra la incertidumbre:

En este caso, nadie se molesta en determinar con precisión la amplitud o la fase. Luego, el círculo de errores se convertirá en una elipse, reduciéndose en una dirección y extendiéndose en la otra:

Esta condición se denomina luz comprimida , ya que las fluctuaciones de amplitud o fase se comprimen a lo largo de uno de los ejes, lo que reduce el error de medición. El primero se llama compresión de amplitud (la elipse se extiende a través del radio, puede medir con precisión la amplitud en los máximos y mínimos de la onda sinusoidal); la segunda fase (elipse a lo largo del radio, puede medir la fase en los ceros de la onda sinusoidal).

¿Por qué es importante?

Para la luz ordinaria, no podemos medir la amplitud o fase con mayor precisión de la que nos da el círculo de errores. Esto se llama nivel de ruido cuántico estándar . La luz comprimida le permite reducir el error en una dirección y "sumergirse" bajo este nivel de ruido. En cierto sentido, podemos [pathos_mode_on] tomar medidas más precisas de lo que a la naturaleza le gustaría [pathos_mode_off].

Un simple ejemplo.

Cada fuente de luz genera un número entero de fotones por segundo. Puede cambiar de segundo a segundo debido a la naturaleza cuántica de la luz, formando la distribución del número de fotones (lo mencioné en la historia sobre Hanbury Brown y Twiss ).

El número de fotones es igual a la intensidad de la luz. Es decir, la intensidad es un poco de "ruido": varía de un segundo a otro. Este es el nivel de ruido cuántico estándar.

Pero si el número de fotones no cambia de segundo a segundo (figura a la derecha), entonces la intensidad es estrictamente constante y sin ningún ruido. Esta será la luz que está máximamente comprimida en amplitud. El flujo de fotones al mismo tiempo se parece a esto:

Es decir, los fotones se emiten estrictamente periódicamente. Si se viola la periodicidad, la luz aún permanece en cierta medida comprimida.

¿Por qué se necesita esto?

A diferencia de otros objetos exóticos, el uso de luz comprimida resultó ser muy prometedor.

Telecom. La transmisión de información mediante la modulación de una variable comprimida (amplitud (AM) o fase (FM), el término de cuadratura más general) le permite aumentar la relación señal / ruido. Es posible construir amplificadores que agreguen ruido solo a esa cuadratura que no está comprimida y no transmite una señal útil.

Entrelazamiento cuántico. En algunos casos, se pueden establecer paralelos entre el enredo de los fotones y la compresión de la luz. Por ejemplo, puede confundir dos haces de luz: uno comprimido en amplitud, el segundo en fase.

Criptografía cuántica. Se deriva del enredo cuántico y la imagen de arriba. En el esquema más simple de criptografía cuántica, Alice transmite información a Bob usando fotones con polarización aleatoria. La dirección de compresión puede desempeñar el papel de compresión: si se selecciona incorrectamente, un atacante que intercepte el canal de comunicación medirá el ruido en lugar de la señal.

Detectores de ondas gravitacionales. Para esta tarea, debe capturar las fluctuaciones más pequeñas de grandes cargas. Esto generalmente se hace usando un interferómetro Michelson. Está construido de manera muy simple: un láser, dos espejos y una placa translúcida:

Un láser se refleja desde dos espejos, interfieren dos reflejos y se forma un patrón de interferencia en la pantalla. Si uno de los espejos se mueve, la imagen también se mueve. Esto sucede debido a un cambio en la fase de la onda: el espejo se ha alejado, la trayectoria del láser se ha vuelto un poco más larga, ha entrado una fase adicional, las tiras de interferencia se han desplazado.

Como el interferómetro mide la fase, su resolución no puede ser mejor que la incertidumbre de la fase. Para un láser convencional, se limita a un nivel de ruido cuántico estándar. Pero si reemplazamos el láser con una fuente de luz comprimida en fase, entonces este problema desaparecerá y podremos medir distancias con una precisión sin precedentes.

Hoy, esto se hace en uno de los detectores de ondas gravitacionales más grandes GEO600 y, aparentemente, está planeado para el detector espacial LISA. Por cierto, entre los usuarios de GT está Shkaff , que solo está haciendo esto y está listo para responder sus preguntas en los comentarios.

Medición de fase precisa. La luz comprimida en fase puede ser útil para mediciones utilizando el método de contraste de fase, una técnica cotidiana en la biología moderna.

¿Cómo generar?

Crear luz comprimida no es tan simple. Para esto, se utilizan procesos ópticos no lineales. Es bastante difícil de explicar con los dedos, pero daré un ejemplo.

En algunos cristales, se observa un efecto llamado no linealidad de Kerr : la dependencia del índice de refracción de la intensidad de la luz. Enviemos un pulso láser a tal cristal. Para cualquier pulso, la intensidad en los frentes es más baja que en el centro, lo que significa que el índice de refracción cambiará más fuertemente donde está ahora el centro del pulso. La diferencia en los índices de refracción conduce al hecho de que la fase de la onda en el centro y en los frentes varía de manera diferente. La totalidad de estos cambios lleva al hecho de que la fase se define un poco mejor de lo habitual, y la intensidad, por el contrario, un poco peor. Hola, luz exprimida :).

¿Cómo detectar?

La luz comprimida también se puede medir de varias maneras.

1. Esquema Hanbury Brown-Twiss.

En una serie sobre Hanbury Brown y Twiss, dije que la función de correlación g ⁽²⁾ corresponde al ancho de la distribución del número de fotones. La compresión de amplitud de la luz significa que la cantidad de fotones se determina mejor de lo habitual. Por lo tanto, en el sentido amplio de la palabra g ^{(2) es} menos que la unidad, un signo de luz exprimida.

2. Detector de equilibrio. Es como un circuito Hanbury Brown-Twiss, pero en lugar de correlaciones, restamos o agregamos señales de dos diodos (a petición nuestra):

Un espejo translúcido transmite o refleja cada fotón al azar. Esta aleatoriedad introduce ruido cuántico adicional (como el ruido de disparo) en la señal . Tal ruido tiene un signo diferente en dos diodos: si se refleja un fotón, entonces no volará; si vuela, no se reflejará.

Si restamos la señal de un diodo de otro, entonces el ruido cuántico no irá a ninguna parte. ¿Y si sumamos? Entonces el ruido desaparecerá, porque tiene un signo diferente. (Otra explicación: dividimos la luz en dos partes, y luego las doblamos hacia atrás; esto, obviamente, no agregó ruido adicional).

Entonces, la resta nos agrega ruido con un nivel cuántico estándar, y la suma no cambia nada. Si la luz estudiada se redujo en amplitud (es decir, "sin ruido"), entonces la resta la hará más ruidosa, y la adición la dejará sin cambios. Al cambiar entre suma y resta, podemos medir el nivel de ruido, y si es diferente, entonces observamos una luz de amplitud reducida.

El ruido después de la suma (rojo) y la resta (azul) se parece a esto. El ruido rojo es mucho más débil y corresponde a la luz comprimida.

3. Homodyning. La compresión de amplitud es fácil de medir, pero ¿qué pasa con la compresión de fase? Si es posible "rotar" la orientación de la elipse (es decir, la fase de la luz), entonces la luz de la fase comprimida se comprimirá en amplitud. La fase se puede girar mezclando la luz con la onda de referencia. Esto es muy similar al oscilador local del receptor, solo en el oscilador local la frecuencia de las ondas de referencia y estudiadas es diferente, pero en el oscilador local no lo es (de ahí el nombre).

Incluso en el homodino, debe seleccionar la fase de la onda de referencia. En electrónica, esto se realiza mediante un cambiador de fase, en óptica mediante una línea de retardo (cuanto más tarde llegue la luz, más se ejecutará la fase). La mezcla tiene lugar en el mismo espejo translúcido:

La onda de referencia viene de abajo. Y luego, el mismo detector equilibrado.

Y de interesante

Hasta ahora, la luz exprimida se usa solo en interferometría ultra precisa. El problema es que es increíblemente frágil. Esto es fácil de entender con el ejemplo de la luz ideal comprimida en amplitud (el flujo de fotones es estrictamente periódico):

En la propagación de la luz, las pérdidas son inevitables, que siempre son accidentales. Esto significa que los fotones desaparecerán de la secuencia al azar:

Como puede ver, casi no queda nada de la periodicidad. Así como de compresión. Por lo tanto, la luz comprimida es muy difícil de transmitir a largas distancias.

Y finalmente, admiremos el esquema del detector gravitacional GEO 600 cerca de Hannover:

La fuente de luz comprimida está sobre un fondo amarillo. Utiliza un proceso óptico no lineal, pero no la no linealidad de Kerr, sino la generación del segundo armónico de la radiación. La línea punteada roja es luz comprimida. Arriba a la derecha hay un interferómetro Michelson con hombros de 600 metros; Los espejos están suspendidos en cargas que deben oscilar a partir de ondas gravitacionales. La imagen del interferómetro se obtiene en el fotodiodo en la esquina inferior derecha.

Fuentes de
M. Fox. Óptica cuántica: una introducción - Oxford University Press, 2006.
Gracias a Shkaff por los comentarios de los expertos.

Imágenes gratis : KDPV , 1 , 2 , 3 , 4 , 5 , 6, 7 , 8 , 9 , 10 .