Measuring Harmony - Analizador de espectro de sonido en STM32L4 Discovery
En una publicación anterior , conectamos una pantalla LCD china barata a la placa de descubrimiento STM32L4 . Ahora intentaremos implementar en esta combinación algo que vaya más allá del parpadeo tradicional de un LED, a saber, un analizador de espectro de sonido que usa el micrófono en el tablero. Al mismo tiempo, le diré cómo usar el sistema operativo FreeRTOS, y por qué es necesario, así como por qué hay 12 notas en una octava musical, y que 53 notas son mejores que 12.
Digitalización de sonido
Queremos recibir la señal del micrófono, calcular su espectro utilizando la transformada rápida de Fourier (FPU para ayudarnos) y mostrar el resultado en la pantalla LCD en forma de 'cascada de colores'. La fuerza del sonido se codificará en color. Dibujaremos una línea de píxeles desde el borde de la pantalla donde el píxel más a la izquierda corresponderá a la frecuencia mínima y el más a la derecha corresponderá al máximo, mientras que la imagen anterior se desplazará una línea, liberando espacio para una nueva línea. Nuestro microcontrolador es demasiado complicado para comenzar desde cero, así que comencemos con un ejemplo del kit STM32Cube llamado DFSDM_AudioRecord. ¿Qué es el DFSDM? Este es el filtro digital para la modulación Sigma-Delta. El hecho es que, a diferencia de los viejos micrófonos analógicos, el de la placa Discovery no da una señal en forma de voltaje proporcional a la presión del sonido,y como una secuencia de ceros y unos con una frecuencia de reloj de varios megahercios. Si pasa esta secuencia a través de un filtro de paso bajo, obtendrá la misma señal analógica. En modelos anteriores de microcontroladores, era necesario hacer un filtro digital para recibir una señal de audio en forma digital. Ahora el microcontrolador tiene un módulo especial para esto, y todo lo que se requiere es configurarlo al inicio del programa. Para hacer esto, puede profundizar en la lectura de la documentación o utilizar un ejemplo listo. Fui por el segundo camino. La siguiente imagen ilustra la estructura interna del programa DFSDM_AudioRecord.En modelos anteriores de microcontroladores, era necesario hacer un filtro digital para recibir una señal de audio en forma digital. Ahora el microcontrolador tiene un módulo especial para esto, y todo lo que se requiere es configurarlo al inicio del programa. Para hacer esto, puede profundizar en la lectura de la documentación o utilizar un ejemplo listo. Fui por el segundo camino. La siguiente imagen ilustra la estructura interna del programa DFSDM_AudioRecord.En modelos anteriores de microcontroladores, era necesario hacer un filtro digital para recibir una señal de audio en forma digital. Ahora el microcontrolador tiene un módulo especial para esto, y todo lo que se requiere es configurarlo al inicio del programa. Para hacer esto, puede profundizar en la lectura de la documentación o utilizar un ejemplo listo. Fui por el segundo camino. La siguiente imagen ilustra la estructura interna del programa DFSDM_AudioRecord.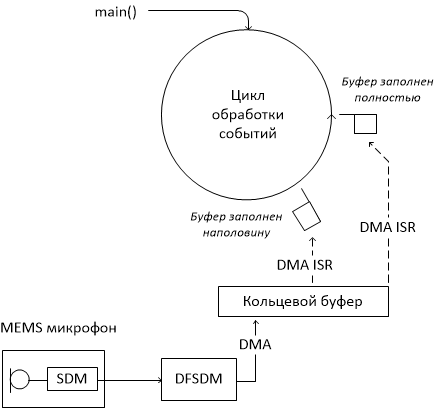 El sonido digitalizado usando DMA cae en el buffer del anillo. DMA provoca una interrupción dos veces: una vez, cuando el búfer está medio lleno, la segunda vez, cuando está lleno. La rutina de interrupción simplemente establece la bandera apropiada. La función main () después de la inicialización ejecuta un bucle infinito donde se comprueban estos indicadores y, si se establece el indicador, se copia la mitad correspondiente del búfer. Un ejemplo copia datos a otro búfer, desde donde se envía nuevamente, usando DMA, al amplificador de auriculares. Dejé esta funcionalidad, agregando el cálculo del espectro de la señal de audio.
El sonido digitalizado usando DMA cae en el buffer del anillo. DMA provoca una interrupción dos veces: una vez, cuando el búfer está medio lleno, la segunda vez, cuando está lleno. La rutina de interrupción simplemente establece la bandera apropiada. La función main () después de la inicialización ejecuta un bucle infinito donde se comprueban estos indicadores y, si se establece el indicador, se copia la mitad correspondiente del búfer. Un ejemplo copia datos a otro búfer, desde donde se envía nuevamente, usando DMA, al amplificador de auriculares. Dejé esta funcionalidad, agregando el cálculo del espectro de la señal de audio.Cuando hay muchas tareas
La forma directa de agregar nuevas funcionalidades a nuestro código es agregar más banderas y escribir funciones que se llamarán si se establecen estas banderas. El resultado suele ser un desorden de indicadores, funciones de controlador y el contexto global, que se ve obligado a ser global, ya que la solución de un problema se divide en muchos pasos pequeños implementados por funciones individuales: controladores de eventos. Una forma alternativa es confiar la gestión de tareas a un sistema operativo, como FreeRTOS. Esto le permite simplificar significativamente la lógica debido al hecho de que cada tarea se resuelve dentro de su propio ciclo de procesamiento de eventos que interactúan entre sí a través de las funciones del sistema operativo. Por ejemplo, podemos agregar una tarea de procesamiento de datos como un ciclo separado,que esperará a que los datos estén listos en la primitiva de sincronización: semáforo. El semáforo es muy simple: puede pasarlo si la marca está marcada y la marca se omite automáticamente. En nuestro caso, la fuente de datos levantará una bandera cuando prepare los datos para otra tarea. De manera similar, puede crear cadenas arbitrarias a partir de tareas de origen de datos y tareas de consumidor de datos, de forma similar a cómo sucede esto, por ejemplo, en el sistema operativo Linux.en el sistema operativo Linux.en el sistema operativo Linux.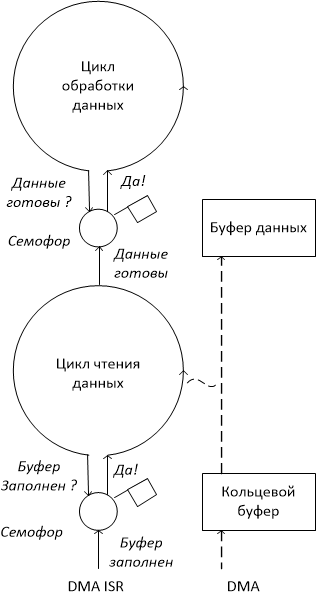 Por supuesto, la ejecución simultánea de tareas es una ilusión, especialmente cuando el núcleo informático es solo uno. En este caso, podemos decir que tenemos un solo hilo de ejecución del programa por parte del procesador. Los semáforos, como otras primitivas de sincronización, desempeñan el papel de un agujero de conejo mágico, en el que el flujo de ejecución no puede surgir en otra tarea.Conectar FreeRTOS a su proyecto es bastante simple. Solo es necesario reemplazar el bucle sin fin, que generalmente finaliza la función main () en el microcontrolador, con una llamada a osKernelStart (). Después de eso, el compilador le explicará exactamente lo que le falta para la compilación. Todas las acciones que realizó anteriormente en el bucle deben transferirse a una tarea separada y registrarse con la llamada xTaskCreate. Después de eso, puede agregar tantas tareas más como desee. Debe tenerse en cuenta que entre las llamadas a xTaskCreate y osKernelStart es mejor no colocar ningún código que funcione con el hardware, ya que aquí el temporizador del sistema puede no funcionar correctamente. La llamada al controlador del temporizador del sistema operativo osSystickHandler () debe agregarse a SysTick_Handler (), y las dos funciones SVC_Handler y PendSV_Handler deben eliminarse de su código,ya que están implementados en el código OS. Al registrar tareas, es importante no cometer un error con el tamaño de la pila. Si resulta ser demasiado pequeño, obtendrá accidentes en los lugares más inesperados. La primera cuando la pila se desborda es la estructura misma que describe la tarea. IAR tiene la capacidad de ver una lista de tareas. Si ve una tarea con un nombre cambiado, debe aumentar el tamaño de la pila.Para calcular el espectro, usamos la transformada rápida de Fourier. La función correspondiente ya está en la biblioteca. Ella recibe un búfer lleno de datos complejos y forma el resultado allí. En consecuencia, en la entrada, ella necesita un búfer, donde el sonido digitalizado se alterna con ceros (parte compleja 0). En la salida, obtenemos números complejos para los que calculamos inmediatamente el cuadrado del módulo al sumar los cuadrados de las partes real e imaginaria. Hacemos esto solo para la mitad del búfer, porque el espectro es simétrico. Necesitaríamos la segunda mitad si quisiéramos hacer la transformación inversa, pero para una simple visualización del espectro no es necesario. Se necesitan algunos esfuerzos adicionales para poder calcular el espectro en diferentes rangos espectrales. Para obtener el espectro para bajas frecuencias,Acumulo datos durante varios ciclos de lectura del búfer, reduciendo efectivamente la frecuencia de muestreo del sonido, que inicialmente es 44.1kHz. El resultado son 6 rangos: 20kHz, 10kHz, 5kHz, 2600Hz, 1300Hz, 650Hz. Para cambiar los rangos, use el joystick y una tarea separada. El joystick también realiza la función de iniciar / detener la 'cascada', así como ajustar la sensibilidad. Es más conveniente mostrar el espectro en unidades logarítmicas (decibelios), porque su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoEl resultado son 6 rangos: 20kHz, 10kHz, 5kHz, 2600Hz, 1300Hz, 650Hz. Para cambiar los rangos, use el joystick y una tarea separada. El joystick también realiza la función de iniciar / detener la 'cascada', así como ajustar la sensibilidad. Es más conveniente mostrar el espectro en unidades logarítmicas (decibelios), porque su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoEl resultado son 6 rangos: 20kHz, 10kHz, 5kHz, 2600Hz, 1300Hz, 650Hz. Para cambiar los rangos, use el joystick y una tarea separada. El joystick también realiza la función de iniciar / detener la 'cascada', así como ajustar la sensibilidad. Es más conveniente mostrar el espectro en unidades logarítmicas (decibelios), ya que su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoEs más conveniente mostrar el espectro en unidades logarítmicas (decibelios), ya que su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoEs más conveniente mostrar el espectro en unidades logarítmicas (decibelios), porque su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoformato para representar un número en float32 . Lo más significativo es un signo. Los siguientes 8 bits son el exponente binario más 127. Los bits restantes son la parte fraccionaria de la mantisa a pesar de que la parte entera es 1 (omitimos los matices de los números desnormalizados por simplicidad). Entonces, habiendo seleccionado el exponente de float32 y agarrado los varios bits más significativos de la mantisa, puede obtener una buena aproximación del logaritmo. Usando la tabla preparada, convertimos el número resultante en un código RGB para mostrar en la pantalla LCD. Resulta una escala de colores de 90 o 60 decibelios. El nivel de volumen correspondiente a cero de esta escala se puede ajustar presionando el joystick hacia arriba y hacia abajo.
Por supuesto, la ejecución simultánea de tareas es una ilusión, especialmente cuando el núcleo informático es solo uno. En este caso, podemos decir que tenemos un solo hilo de ejecución del programa por parte del procesador. Los semáforos, como otras primitivas de sincronización, desempeñan el papel de un agujero de conejo mágico, en el que el flujo de ejecución no puede surgir en otra tarea.Conectar FreeRTOS a su proyecto es bastante simple. Solo es necesario reemplazar el bucle sin fin, que generalmente finaliza la función main () en el microcontrolador, con una llamada a osKernelStart (). Después de eso, el compilador le explicará exactamente lo que le falta para la compilación. Todas las acciones que realizó anteriormente en el bucle deben transferirse a una tarea separada y registrarse con la llamada xTaskCreate. Después de eso, puede agregar tantas tareas más como desee. Debe tenerse en cuenta que entre las llamadas a xTaskCreate y osKernelStart es mejor no colocar ningún código que funcione con el hardware, ya que aquí el temporizador del sistema puede no funcionar correctamente. La llamada al controlador del temporizador del sistema operativo osSystickHandler () debe agregarse a SysTick_Handler (), y las dos funciones SVC_Handler y PendSV_Handler deben eliminarse de su código,ya que están implementados en el código OS. Al registrar tareas, es importante no cometer un error con el tamaño de la pila. Si resulta ser demasiado pequeño, obtendrá accidentes en los lugares más inesperados. La primera cuando la pila se desborda es la estructura misma que describe la tarea. IAR tiene la capacidad de ver una lista de tareas. Si ve una tarea con un nombre cambiado, debe aumentar el tamaño de la pila.Para calcular el espectro, usamos la transformada rápida de Fourier. La función correspondiente ya está en la biblioteca. Ella recibe un búfer lleno de datos complejos y forma el resultado allí. En consecuencia, en la entrada, ella necesita un búfer, donde el sonido digitalizado se alterna con ceros (parte compleja 0). En la salida, obtenemos números complejos para los que calculamos inmediatamente el cuadrado del módulo al sumar los cuadrados de las partes real e imaginaria. Hacemos esto solo para la mitad del búfer, porque el espectro es simétrico. Necesitaríamos la segunda mitad si quisiéramos hacer la transformación inversa, pero para una simple visualización del espectro no es necesario. Se necesitan algunos esfuerzos adicionales para poder calcular el espectro en diferentes rangos espectrales. Para obtener el espectro para bajas frecuencias,Acumulo datos durante varios ciclos de lectura del búfer, reduciendo efectivamente la frecuencia de muestreo del sonido, que inicialmente es 44.1kHz. El resultado son 6 rangos: 20kHz, 10kHz, 5kHz, 2600Hz, 1300Hz, 650Hz. Para cambiar los rangos, use el joystick y una tarea separada. El joystick también realiza la función de iniciar / detener la 'cascada', así como ajustar la sensibilidad. Es más conveniente mostrar el espectro en unidades logarítmicas (decibelios), porque su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoEl resultado son 6 rangos: 20kHz, 10kHz, 5kHz, 2600Hz, 1300Hz, 650Hz. Para cambiar los rangos, use el joystick y una tarea separada. El joystick también realiza la función de iniciar / detener la 'cascada', así como ajustar la sensibilidad. Es más conveniente mostrar el espectro en unidades logarítmicas (decibelios), porque su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoEl resultado son 6 rangos: 20kHz, 10kHz, 5kHz, 2600Hz, 1300Hz, 650Hz. Para cambiar los rangos, use el joystick y una tarea separada. El joystick también realiza la función de iniciar / detener la 'cascada', así como ajustar la sensibilidad. Es más conveniente mostrar el espectro en unidades logarítmicas (decibelios), ya que su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoEs más conveniente mostrar el espectro en unidades logarítmicas (decibelios), ya que su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoEs más conveniente mostrar el espectro en unidades logarítmicas (decibelios), porque su rango dinámico generalmente es muy grande, y en una escala lineal podemos distinguir solo los componentes más fuertes del espectro. El logaritmo se considera bastante tiempo incluso en FPU, por lo que reemplacé el logaritmo real con una aproximación lineal por partes, que es fácil de obtener, sabiendoformato para representar un número en float32 . Lo más significativo es un signo. Los siguientes 8 bits son el exponente binario más 127. Los bits restantes son la parte fraccionaria de la mantisa a pesar de que la parte entera es 1 (omitimos los matices de los números desnormalizados por simplicidad). Entonces, habiendo seleccionado el exponente de float32 y agarrado los varios bits más significativos de la mantisa, puede obtener una buena aproximación del logaritmo. Usando la tabla preparada, convertimos el número resultante en un código RGB para mostrar en la pantalla LCD. Resulta una escala de colores de 90 o 60 decibelios. El nivel de volumen correspondiente a cero de esta escala se puede ajustar presionando el joystick hacia arriba y hacia abajo.Mostramos una imagen sobre los beneficios de leer hojas de datos
Ahora solo tenemos que mostrar la imagen y revivir nuestra 'cascada'. La forma más sencilla de hacerlo es almacenar la imagen de toda la pantalla en un búfer, actualizarla allí y volver a dibujarla cada vez que aparezcan nuevos datos. Esta solución no solo es extremadamente ineficiente, sino que tampoco tenemos suficiente memoria para almacenar la imagen completa. Parece que la pantalla LCD en sí misma tiene suficiente memoria para esto, y debería ser capaz de hacer algo interesante con ella. De hecho, el estudio de la hoja de datospermite detectar el comando de desplazamiento hasta ahora no utilizado, que le permite cambiar dinámicamente la forma en que se muestra la memoria del controlador LCD en la pantalla. Imagina que la memoria es una cinta encerrada en un anillo que ves debajo del cristal de la pantalla. El comando Dirección de inicio de desplazamiento vertical (0x37) le permite establecer la posición en la cinta correspondiente al borde superior de la pantalla. Entonces, todo lo que necesitamos para revivir la 'cascada' es grabar un nuevo espectro en esta posición y desplazarse por la cinta de memoria. El código correspondiente se agregó al controlador LCD, se tomó prestado del reputado Peter Drescher y se adaptó como se describe aquí.. El único inconveniente de este enfoque: el desplazamiento funciona solo en el lado largo de la pantalla. En consecuencia, solo el lado corto está disponible para la salida del espectro.12 ?
Pasemos a las aplicaciones prácticas de nuestro dispositivo. Lo primero que es fácil de ver en el espectro son los armónicos, es decir, las frecuencias que son múltiplos de la frecuencia fundamental. Especialmente muchos de ellos en la voz. También hay en los sonidos que hacen instrumentos musicales. Es fácil entender por qué las notas de las octavas vecinas difieren en frecuencia en 2 veces: entonces las notas de una octava más alta coinciden en frecuencia con el segundo armónico de las notas de una octava baja. Dicen que al mismo tiempo suenan "al unísono". Es un poco más difícil de entender por qué hay 12 notas en una octava: siete principales (teclas blancas en el teclado del piano) más 5 adicionales (teclas negras). Las notas adicionales están indicadas por las notas principales con caracteres agudos y planos, aunque en realidad no hay diferencia entre ellas y las notas principales: las 12 notas forman una progresión geométrica, por lo queque la proporción de frecuencias entre notas adyacentes es igual a la raíz del duodécimo grado de 2. El significado de esta división de la octava en notas es que para cualquier nota hay otras notas que difieren en frecuencia una vez y media, esta combinación se llama quinta. Las notas que componen la quinta nota suenan al unísono porque el segundo armónico de una nota coincide en frecuencia con el tercer armónico de la otra nota. La foto a continuación muestra los espectros de las notas Do y Sol, formando un quinto, los armónicos coincidentes están encerrados en amarillo.formando un quinto, los armónicos coincidentes están rodeados en amarillo.formando un quinto, los armónicos coincidentes están rodeados en amarillo. ¿Cómo es que las notas 12? Como las notas forman una progresión geométrica, pasamos a los logaritmos. ln (1.5) / ln (2) = 0.58496 ... Se obtiene un valor cercano para la fracción 7/12 = 0.583 ... Es decir, siete medios tonos (intervalos entre notas adyacentes) resultan estar muy cerca de una quint - 1.498. Curiosamente, la fracción 31/53 = 0.58491 .. da una precisión mucho mayor, de modo que el quinto es diferente de 1.5 solo en el quinto decimal. Este hecho no pasó desapercibido, pero los instrumentos musicales con 53 notas en una octava no recibieron distribución. Son difíciles de sintonizar, son difíciles de tocar y el porcentaje de personas que pueden sentir la diferencia con las herramientas convencionales es muy pequeño.
¿Cómo es que las notas 12? Como las notas forman una progresión geométrica, pasamos a los logaritmos. ln (1.5) / ln (2) = 0.58496 ... Se obtiene un valor cercano para la fracción 7/12 = 0.583 ... Es decir, siete medios tonos (intervalos entre notas adyacentes) resultan estar muy cerca de una quint - 1.498. Curiosamente, la fracción 31/53 = 0.58491 .. da una precisión mucho mayor, de modo que el quinto es diferente de 1.5 solo en el quinto decimal. Este hecho no pasó desapercibido, pero los instrumentos musicales con 53 notas en una octava no recibieron distribución. Son difíciles de sintonizar, son difíciles de tocar y el porcentaje de personas que pueden sentir la diferencia con las herramientas convencionales es muy pequeño.Código fuente
Mentiras aqui . Para la compilación se utilizó IAR Embedded Workbench para ARM 7.50.2. No se requieren otras bibliotecas para la compilación. Source: https://habr.com/ru/post/es391311/
All Articles