Tejido cuántico espacio-tiempo: red de tapices
Cómo los pares cuánticos cosen el espacio-tiempo
La primera parte,Brian Swingle estudió física en la escuela de posgrado del Instituto de Tecnología de Massachusetts, cuando decidió tomar un par de clases de teoría de cuerdas para mejorar su educación, como recuerda, sobre el principio de "por qué no", aunque inicialmente no prestó atención a los conceptos. a quien conoció en este curso. Pero al hundirse más, comenzó a notar conexiones inesperadas con su propio trabajo, en el que utilizó el llamado Redes tensoras para predecir las propiedades de materiales exóticos y un enfoque de la física de los agujeros negros y la gravedad cuántica, tomado de la teoría de cuerdas. "Me di cuenta de que algo increíble estaba sucediendo", dice.Los tensores surgen periódicamente de forma inesperada en diferentes áreas de la física: estos son objetos matemáticos que pueden representar muchos números a la vez. Por ejemplo, el vector de velocidad es el tensor más simple: incluye tanto la velocidad como la dirección. Los tensores más complejos conectados en la red se pueden utilizar para simplificar los cálculos para sistemas complejos compuestos de muchas partes que interactúan, incluidas las intrincadas interacciones de una gran cantidad de partículas subatómicas que forman la materia.Swing es uno de un número cada vez mayor de físicos que ven el valor de aplicar redes tensoras a la cosmología. Entre otros beneficios, esto puede ayudar a resolver el debate en curso sobre la esencia del espacio-tiempo. John PreskillEl profesor Richard Feynman, de Física Teórica en KalTech, creía que muchos físicos sospechaban una profunda conexión entre el enredo cuántico, la aterradora acción de largo alcance que enfureció tanto a Einstein, y la geometría del espacio-tiempo en las escalas más pequeñas. Esto ha estado sucediendo desde que John Wheeler, hace sesenta años, describió por primera vez el espacio-tiempo como espuma burbujeante. "Si estudias geometría en una escala comparable a las escalas de Planck", a las distancias más cortas posibles, "se parece cada vez menos al espacio-tiempo", dice Preskill. "Esto no es geometría en absoluto, sino algo más, algo que surge de cosas más fundamentales".Los físicos continúan luchando con el problema confuso de cuál podría ser este problema más fundamental, pero sospechan que está relacionado con la información cuántica. "Cuando hablamos de codificación de información, queremos decir que puedes dividir el sistema en partes y habrá una correlación entre ellas que puedo aprender algo sobre una de las partes, observando la otra", dice Preskill. Esta es la esencia de la confusión.A menudo hablan del "tejido" del espacio-tiempo, y esta metáfora conduce al concepto de unir hilos individuales para formar un todo liso. Estos hilos son esencialmente cuánticos. "El enredo es el tejido del espacio-tiempo", dice Swingle, que actualmente trabaja en investigación en Stanford. - Este es un hilo que une todo el sistema, asegurando la diferencia entre propiedades generales y propiedades de entidades individuales. Pero para ver realmente un comportamiento colaborativo interesante, debe comprender cómo se distribuye el enredo ”.Las redes tensoras proporcionan una herramienta matemática que puede hacer precisamente eso. Desde este punto de vista, el espacio-tiempo surge de conjuntos de nodos de una red compleja conectados entre sí.donde pequeñas piezas de información cuántica encajan juntas como Lego. El enredo es el pegamento que conecta la red. Para comprender el espacio-tiempo, primero es necesario considerar el enredo desde posiciones geométricas, ya que así es como se codifica la información en una gran cantidad de nodos del sistema que interactúan.Muchos cuerpos, una red
Modelar un sistema cuántico complejo no es broma; Incluso un sistema clásico con más de dos partes que interactúan ya es bastante complicado para el modelado. Cuando Isaac Newton publicó sus Principia [Principios matemáticos de la filosofía natural] en 1687, uno de los temas del libro fue el "problema de los tres cuerpos". La tarea de calcular el movimiento de dos objetos, por ejemplo, el Sol y la Tierra, teniendo en cuenta su atracción mutua, es relativamente simple. Pero si le agrega un tercer cuerpo, por ejemplo, la Luna, se convierte de una tarea simple con una solución exacta a una caótica, donde las predicciones a largo plazo requieren potentes sistemas informáticos para simular la evolución aproximada del sistema. Y cuantos más objetos hay en el sistema, más complicados son los cálculos, y su complejidad crece casi linealmente, al menos en física clásica.Ahora imagine un sistema cuántico con miles de millones de átomos, cada uno de los cuales interactúa con otros de acuerdo con ecuaciones cuánticas complejas. En esta escala, la complejidad parece crecer exponencialmente con el número de partículas en el sistema, por lo que el enfoque de la fuerza bruta a la informática simplemente no funcionará.Imagina una pepita de oro. Se compone de miles de millones de átomos, y todos interactúan entre sí. A partir de estas interacciones, se siguen varias propiedades clásicas del metal: color, resistencia o conductividad. "Los átomos son pequeñas cosas que obedecen a la mecánica cuántica, y cuando los juntas, suceden cosas nuevas y sorprendentes", dice Swingle. Pero a esta escala, las reglas de la mecánica cuántica comienzan a funcionar. Los físicos necesitan calcular con precisión la función de onda de esta pepita, que describe el estado del sistema. Y esta función es una hidra de múltiples cabezas de complejidad exponencial.Incluso si solo hay cien átomos en la pepita y cada uno tiene un giro cuántico que toma uno de dos estados, arriba o abajo, el número total de estados posibles ya será de 2,100millones de billones de billones. Y con la adición de cada átomo, la tarea empeora exponencialmente. (Y empeora aún más cuando intentas describir algo distinto de los giros, como debería hacer cualquier modelo realista). "Si toma todo el Universo visible y lo llena con los mejores discos disponibles, los mejores discos duros, puede almacenar solo 300 giros en ellos", dice Swingle. - Hay información, pero no toda corresponde a la física. Nadie ha medido nunca estos números ".Las redes tensoras permiten a los físicos comprimir toda la información contenida en la función de onda y concentrarse solo en aquellas propiedades que pueden medirse experimentalmente: qué tan fuertemente el material refracta la luz, o qué tan bien absorbe el sonido, o cómo conduce la electricidad. Un tensor es un cuadro negro que toma un conjunto de números y da otro. Por lo tanto, puede conectar una función de onda simple, por ejemplo, un conjunto de electrones que no interactúan entre sí en un estado con la energía más baja, y procesarla con tensores una y otra vez hasta que el proceso produzca una función de onda para un sistema grande y complejo, como miles de millones que interactúan en pepita de oro de los átomos. El resultado es un diagrama simple que representa esta pepita compleja: innovación,comparable a los diagramas desarrollados por Feynman a mediados del siglo XX que simplificaron la representación de las interacciones de partículas. Y la red tensora tiene su propia geometría, así como espacio-tiempo.La clave para la simplificación radica en el principio de "localidad". Cada electrón individual interactúa solo con los electrones más cercanos. El enredo de cada electrón con sus vecinos da un conjunto de "nodos" de la red. Estos nodos son tensores y los enredos los unen. Todos estos nodos interconectados forman la red. Los cálculos complejos se vuelven más fáciles de visualizar. A veces todo se reduce a una tarea de conteo más simple.Existen muchos tipos diferentes de redes tensoras, pero entre las más útiles hay una conocida por la abreviatura MERA (renormalización de anzats de enredos multiescala). El principio de su funcionamiento es el siguiente: imagine una línea unidimensional de electrones. Reemplace ocho electrones diferentes, denotándolos por A, B, C, D, E, F, G y H, con las unidades fundamentales de información cuántica (qubits) y enrede cada uno de ellos con un vecino para formar enlaces. A se confunde con B, C con D, y así sucesivamente. Esto da como resultado una red de nivel superior. Luego, confunda AB con CD y EF con GH para subir otra capa de la red. Y finalmente, ABCD se confunde con EFGH para formar el nivel más alto. "En cierto sentido, podemos decir que el enredo se utiliza para construir la función de onda de muchos cuerpos", escribió Roman Orus en su trabajo el año pasado [Román Orús ], físico de la Universidad. Johannes Gutenberg (Alemania).¿Por qué algunos físicos son tan optimistas sobre el potencial de las redes tensoras, especialmente MERA, que pueden llevarlos a la gravedad cuántica? Porque las redes muestran cómo una estructura geométrica simple puede emerger de interacciones complejas entre muchos objetos. Y Swingle con personas de ideas afines espera que se pueda usar esta nueva geometría, mostrando cómo explica el mecanismo por el cual las piezas individuales de información cuántica se transforman en un espacio-tiempo continuo y suave.Límites espacio-temporales
Al desarrollar redes tensoras, los expertos en física de la materia condensada descubrieron accidentalmente una dimensión adicional: esta técnica conduce a la aparición de sistemas bidimensionales en una dimensión. Y los expertos en la teoría de la gravedad eliminaron una dimensión, pasando de tres a dos, desarrollando el llamado principio holográfico Estos dos conceptos pueden unirse y crear una visión más compleja del espacio-tiempo.En la década de 1970, el físico Jacob Bekenstein mostró que la información sobre el interior de un agujero negro está codificada en su superficie plana de dos dimensiones (en el límite), y no en su volumen tridimensional. Veinte años después, Leonard Susskind y Gerard 't Hooft [Leonard Susskind y Gerard' t Hooft] expandieron este concepto a todo el universo, equiparándolo a un holograma: nuestro universo tridimensional en todo su esplendor surge de un "código fuente" bidimensional. En 1997, Juan Maldacena encontró un ejemplo concreto del funcionamiento de un holograma, demostrando que el modelo de juguete para describir un espacio plano sin gravedad es equivalente a describir un espacio en forma de silla de montar con gravedad. Esta relación de física se llama "dualidad".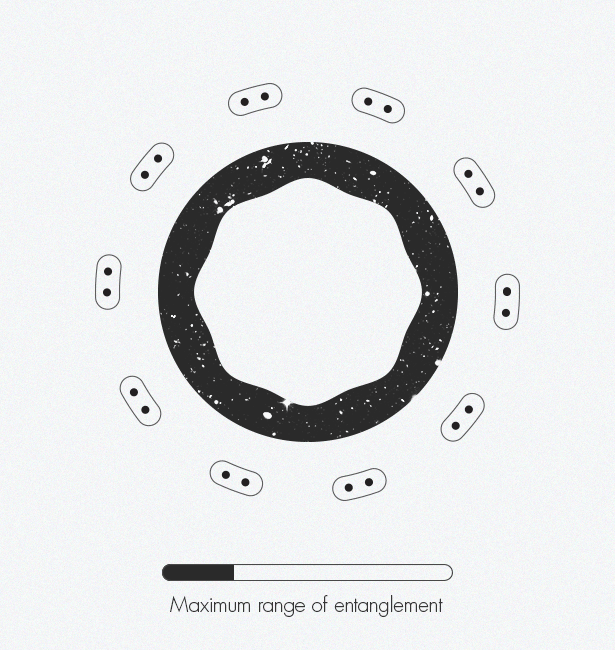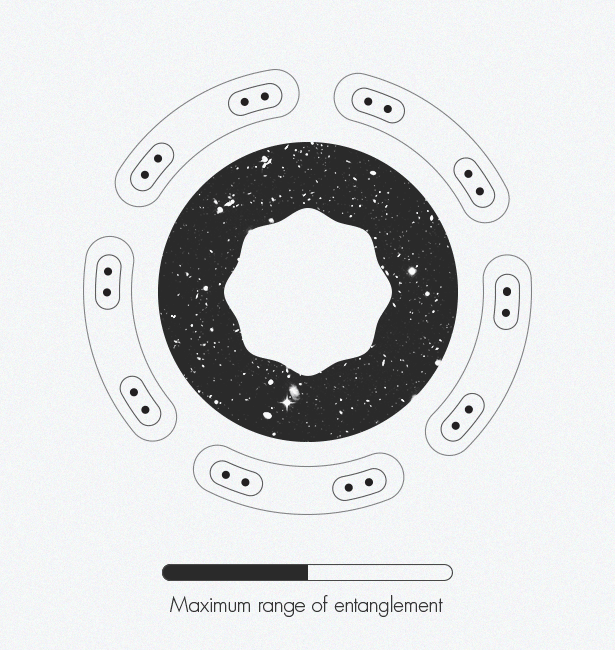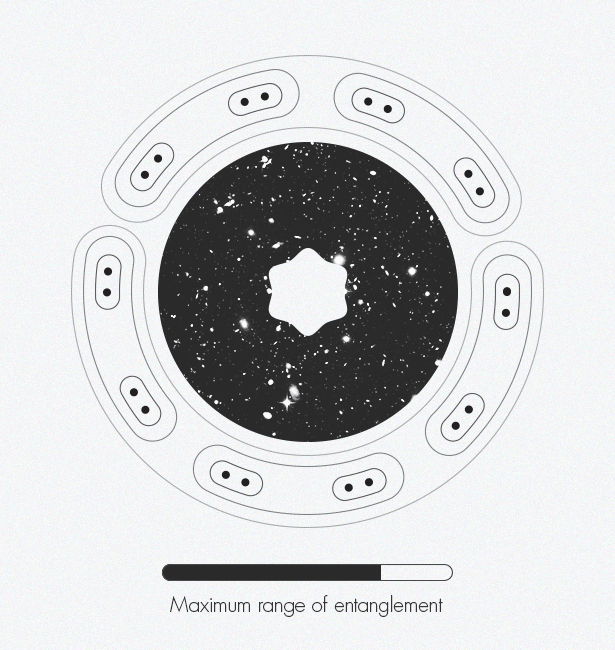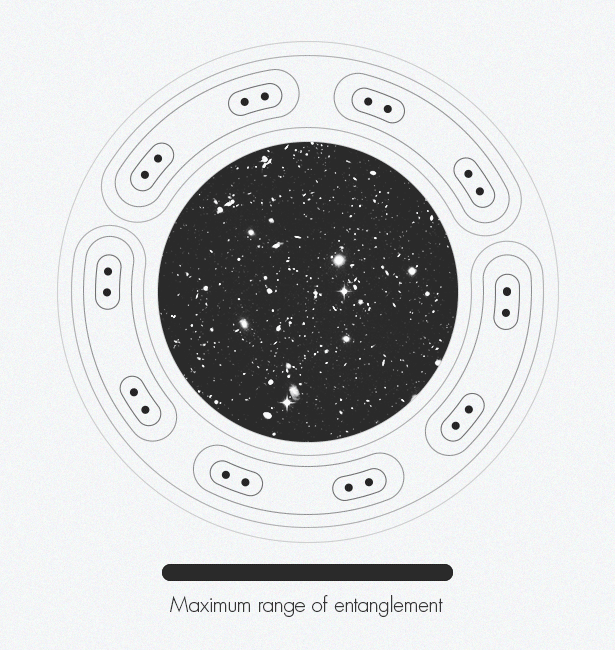
Mark Van Raamsdonk [ Mark Van Raamsdonk] representa cómo el enredo crea gradualmente el espacio-tiempo. A lo largo de los bordes de la figura, las partículas de puntos individuales comienzan a enredarse entre sí. Estos pares enredados se enredan con otros pares. A medida que más y más pares se enredan, aparece una estructura espacio-temporal.Mark van Raamsdonck, especialista en teoría de cuerdas de la Universidad de Columbia Británica (Vancouver), compara este principio holográfico con un chip de computadora bidimensional que contiene código para crear un mundo virtual tridimensional en un juego de computadora. Vivimos dentro del espacio tridimensional del juego. En cierto sentido, nuestro espacio es ilusorio y es solo una imagen efímera que cuelga en el aire. Pero van Raamsdonck enfatiza que "todavía hay algún tipo de entidad física en la computadora que almacena toda la información".La idea ha sido ampliamente aceptada entre los físicos teóricos, pero todavía están luchando con cómo exactamente las dimensiones más pequeñas almacenan información sobre la geometría del espacio-tiempo. El problema es que nuestro chip de computadora metafórico debe ser algún tipo de computadora cuántica, en la cual los ceros y unos habituales se reemplazan por qubits, capaces de representar simultáneamente todos los estados posibles de cero a uno. Estos qubits deben estar enredados, de modo que el estado de un qubit esté determinado por el estado de su vecino, antes de que se pueda codificar un mundo tridimensional realista.Del mismo modo, el enredo parece ser una característica fundamental del espacio-tiempo. Dos científicos llegaron a esta conclusión en 2006: Shinsei Ryu [Universidad de Illinois] y Tadashi Takayanagi (Universidad de Kyoto) que compartieron el premio Nuevos Horizontes de Física en 2015. "La idea es que la forma en que se codifica la geometría del espacio-tiempo está fuertemente relacionada con la forma en que las diferentes partes de este chip están enredadas entre sí", explica Van Raamsdonk.Inspirado por su trabajo, así como por el trabajo de Maldasena que siguió, en 2010, Van Raamsdonk propuso un experimento mental que demuestra el papel crítico del enredo en la formación del espacio-tiempo. Investigó lo que sucedería si dividiera el chip de la computadora por la mitad y luego eliminara el enredo entre los qubits en las dos mitades. Descubrió que el espacio-tiempo comienza a colapsar de la misma manera que estirar un chicle por sus extremos conduce a una brecha en el medio. Dividir este chip en piezas cada vez más pequeñas rompe el espacio de tiempo hasta que solo queden piezas separadas y no conectadas. "Si eliminas la confusión, el espacio-tiempo simplemente se desmorona", dice Van Raamsdonk. Del mismo modo, "si quieres construir espacio-tiempo,tienes que confundir qubits de cierta manera ".Combina estos pensamientos con el trabajo de Swingle, vinculando la intrincada estructura del espacio-tiempo y el principio holográfico con redes tensoras y otra pieza del rompecabezas encaja en su lugar. El espacio-tiempo curvo surge naturalmente del enredo en redes tensoras a través de la holografía. "El espacio-tiempo es la representación geométrica de esta información cuántica", dice van Raamsdonk.¿Y cómo se ve esta geometría? En el caso del espacio-tiempo en forma de silla de montar de Maldasena, parece uno de los dibujos "límite - círculo" de Escher de los años 1950-1960. Escher ha estado interesado durante mucho tiempo en el orden y la simetría, incluidos estos conceptos matemáticos en su trabajo desde 1936, cuando visitó el conjunto arquitectónico y de parques de la Alhambra en España y encontró inspiración en los patrones de mosaicos repetidos allí, típicos de la arquitectura árabe, conocidos como mosaicos.Sus grabados en el árbol "límite - círculo" ilustran geometrías hiperbólicas: la distorsión del espacio con curvatura negativa en la superficie bidimensional del disco se asemeja al aplanamiento de un globo a un mapa bidimensional de la Tierra, distorsionando la forma de los continentes. Por ejemplo, " límite - círculo IV"(el infierno y el paraíso) se parecen a muchas figuras repetidas de ángeles y demonios. En el espacio hiperbólico, el tamaño de todas las figuras sería el mismo, pero en las representaciones bidimensionales de Escher, las figuras en el borde parecen más pequeñas que en el centro. El diagrama de la red tensora se parece mucho al límite de la serie" - círculo ", una representación visual de las conexiones profundas que Swing encontró mientras asistía a esas mismas clases de teoría de cuerdas.Hoy, el análisis tensorial se limita a modelar el espacio-tiempo (como en Maldasena), que no describe el Universo en el que vivimos, no tiene la forma de una silla de montar y su expansión se acelera. Los físicos pueden traducir entre modelos solo en casos separados y especiales. Idealmente, necesitan un "diccionario" universal. Y les gustaría derivar este diccionario directamente, sin usar aproximaciones. "Estábamos en una posición divertida con estas dualidades porque todos están de acuerdo en que son muy importantes, pero nadie sabe cómo sacarlas", dice Preskill. “Quizás el enfoque de las redes tensoras hará posible un mayor progreso. Creo que una señal de progreso sería si pudiéramos decir, incluso en el caso de un modelo de juguete: '¡Ajá! ¡Aquí está, la conclusión del diccionario! Sería una pista seria de que nos encontramos con algo importante ".Durante el año pasado, Swingle y van Raamsdonk han trabajado juntos para promover su trabajo en un área que se extiende desde una representación estática del espacio-tiempo a una dinámica. Están interesados en cómo el espacio-tiempo cambia con el tiempo y cómo se dobla en respuesta a estos cambios. Hasta ahora han logrado derivar las ecuaciones de Einstein, específicamente, el principio de equivalencia. Esto demuestra que la dinámica del espacio-tiempo, como su geometría, se basa en intrincados qubits. El comienzo es prometedor."La pregunta '¿Qué es el espacio-tiempo?' parece absolutamente filosófico, dice van Raamsdonk. "De hecho, encontrar una respuesta concreta y que le permita calcular el espacio-tiempo, sería increíble".Source: https://habr.com/ru/post/es396389/
All Articles