¿Quieres acertar a un jugador de ajedrez principiante?Pídale que haga jaque mate con un caballo y un elefante.¿Quieres desconcertar a un programador novato?Pídale que calcule la alfombra con un caballo y un elefante.
Los problemas de ajedrez excitan la imaginación del programador, por loque para la demostración práctica de combinatoriaelegí el problema de ajedrez más difícil del ciclo "jaque mate al rey solitario".Establecimiento de objetivos
El objetivo del proyecto es crear una base de solución, es decir, una lista de los movimientos correctos para todas las ubicaciones posibles del rey blanco, el elefante, el caballo y el rey negro en el tablero de ajedrez.En esta publicación, le diré cómo resolví este problema, qué dificultades tuve que enfrentar y también demostraré lo que sucedió al final. Tecnologías utilizadas: C #, JavaScript, PHP, HTML, CSS.Siendo un jugador de ajedrez muy mediocre, nunca aprendí a hacer jaque mate rápidamente con un caballo y un elefante. Por lo tanto, decidí compensar esta deficiencia con mis habilidades de programación, ordenar todas las posiciones posibles y encontrar el movimiento correcto para cada una.Antes de escribir al menos una línea de código, elaboré un plan "napoleónico" sobre cómo lo haría durante varias semanas. Realmente quería comenzar a resolver este problema desde el final, clasificando todas las combinaciones mate. Y luego retroceda un paso hasta que se agoten todas las opciones posibles.Cuantas opciones hay?
Hay 64 celdas en un tablero de ajedrez. Tenemos cuatro figuras.El número de combinaciones posibles es 64 * 64 * 64 * 64 = 16,777,216.Solo puedes dejar un elefante de pecho blanco.El número de opciones se reducirá a la mitad: 64 * 32 * 64 * 64 = 8,388,608.Tantos puestos estarán en nuestra base de datos de soluciones.De hecho, hay incluso menos combinaciones: dos piezas no pueden pararse en una casilla, los reyes no pueden pararse en las casillas vecinas, el rey negro no puede estar bajo el control, y así sucesivamente. Mirando hacia el futuro, diré que la base de datos de soluciones resultó ser 5,609,790 combinaciones, la matriz se completará en un 67%.Sin embargo, para simplificar el algoritmo y acelerar el acceso a los datos de la base de datos, decidí no "perder el tiempo" y crear una matriz de cuatro dimensiones para todas las combinaciones.La siguiente estructura se define para almacenar cada combinación: struct Combo
{
public Coord whiteKing;
public Coord whiteBishop;
public Coord whiteKnight;
public Coord blackKing;
}
En el interior, se usa otra estructura Coord para registrar las coordenadas de la figura, con la capacidad de calcular el índice de 0 a 63, así como con un operador de comparación sobrecargado. public struct Coord
{
public byte x;
public byte y;
public int index
{
get { return x + y * 8; }
set { x = (byte) (value % 8);
y = (byte) (value / 8); }
}
public static bool operator == (Coord a, Coord b)
{
return a.x == b.x && a.y == b.y;
}
}
Esta estructura resultó ser muy conveniente para pasar como argumento a varias funciones auxiliares, por ejemplo: bool isCheck (Combo combo);
bool isCheckmate (Combo combo);
bool isCheckByBishop (Combo combo);
Sin embargo, para registrar el resultado de la base de decisiones de esta estructura no es suficiente, todavía necesitamos ...Caja blanca
El objetivo de nuestro programa será crear un "recuadro blanco", en el que se sumarán todas las posiciones en las que el "movimiento es blanco", y para el que se sabe qué movimiento tomar, y a través de cuántos movimientos se garantizará el jaque mate.Una parte integral de la "caja blanca" es la siguiente estructura: struct WhitesMove
{
public Combo combo;
public byte moves;
public Coord moveFrom;
public Coord moveTo;
}
La forma más fácil de organizar un "cuadro blanco" es abrir una matriz de cuatro dimensiones. Cada dimensión de esta matriz corresponde a la posible posición de cada figura: WhitesMove [ , , , ] box = new WhitesMove [64, 32, 64, 64];
La primera dimensión es la coordenada del rey blanco.la segunda dimensión es la coordenada del elefante blanco / 2. latercera dimensión es la coordenada del caballo blanco.La cuarta dimensión es la coordenada del rey negro.Lo principal es no confundir su orden :) La matriz se descargará en un 33%, pero es muy conveniente para el procesamiento. Es en esta matriz que se almacenarán 8.388.608 entradas para resolver combinaciones.Por cierto, antes de comenzar a escribir todos los algoritmos de búsqueda, creé un proyecto vacío e inicialicé esta matriz de cuatro dimensiones, para asegurarme de que hay suficiente memoria y no será necesario inventar algo adicional. Aparentemente, la experiencia de participar en olimpiadas informáticas del milenio pasado, donde el tamaño de la estructura no podía exceder los 64 kilobytes, afectó a Turbo Pascal 7.0.Idea del algoritmo
Describa brevemente la idea principal de resolver este problema. Se basa en un algoritmo de búsqueda de amplitud, que tuvo que modificarse un poco, ya que dos personas juegan al ajedrez y los movimientos se hacen a su vez. Por lo tanto, en lugar de una línea, necesitamos dos: "negro" y "blanco". Queue<BlacksMove> blackQueue = new Queue<BlacksMove>();
Queue<WhitesMove> whiteQueue = new Queue<WhitesMove>();
Con la estructura de WhitesMove ya nos hemos encontrado. La estructura de BlacksMove es un poco más simple, ya que no es necesario almacenar el último movimiento de Black en ella.struct BlacksMove
{
public Combo combo;
public byte moves;
}
Primero, en la "línea negra" colocaremos todas las posiciones mate en las que el movimiento es negro. Luego, desde cada posición, haremos un movimiento inverso para las blancas y formaremos una "línea blanca", una lista de posiciones en las que las blancas se mueven.Estos pasos deberán repetirse hasta que se agoten todas las combinaciones posibles.El algoritmo principal en forma de pseudocódigo: " ", " ", " "
" "
{
" "
" "
" "
" "
" "
" "
" "
" "
" "
} " "
" "
Posición mate
La creación de la base de los movimientos correctos comienza con una búsqueda de todas las combinaciones mate. El uso de enumeradores permitió describir con bastante eficacia este proceso. foreach (Combo combo in AllCheckmates())
{
BlacksMove checkmate = new BlacksMove { combo = combo, moves = 0 };
blackQueue.Enqueue(checkmate);
}
Total encontrado 232 posiciones mate. Déjame recordarte que nos limitamos solo a un elefante de campo blanco.Algunos de ellos son bastante exóticos, inexistentes y "cooperativos", esto es cuando el propio rey negro se metió debajo de la estera.
Los jugadores de ajedrez son conscientes de que una estera con un caballo y un elefante de campo blanco debe colocarse en una esquina blanca. En la esquina negra, el jaque mate solo es posible si las negras juegan a lo largo. Especialmente publiqué una foto con un pseudo-autómata al comienzo del artículo para provocar la atención de jugadores de ajedrez reales :)Mat en un movimiento
El siguiente paso es revertir el blanco. Es decir, para cada posición mate encontrada, haga que todos los movimientos blancos posibles retrocedan .¿Cómo hacer un movimiento inverso? Dado que no se proporciona ninguna captura en nuestras posiciones, el algoritmo es bastante simple: haga cualquier movimiento por parte de White, después de lo cual no habrá control para el rey negro.Todas las posiciones encontradas de esta manera ya se pueden poner en el "cuadro blanco", lo que indica que hay un movimiento antes del tapete, y qué tipo de movimiento hacer esto. En el camino, colocamos las combinaciones que se encuentran en la "línea negra".Así es como se ve esta parte del algoritmo:
while (blackQueue.Count > 0)
{
BlacksMove black = blackQueue.Dequeue();
foreach (WhitesMove white in AllWhiteBackMoves(black))
if (!isCheck(white.combo))
if (!whiteBox.Exists(white.combo))
{
whiteBox.Put (white);
whiteQueue.Enqueue(white);
}
}
Por cierto, sobre el rendimientoyield- , , :
IEnumerable<WhitesMove> AllWhiteBackMoves(BlacksMove black)
{
foreach (WhitesMove white in AllWhiteKingMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteBishopMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteKnightMoves(black))
yield return white;
}
Se encontraron un total de 920 posiciones de este tipo, aquí están las más interesantes: movimiento decaballo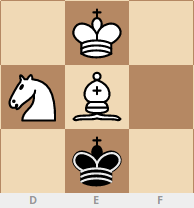
:
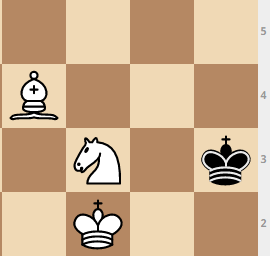
movimiento de elefante : movimiento de rey: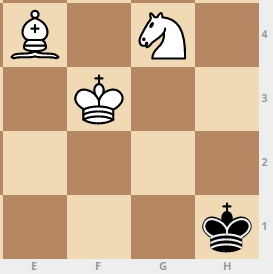
Mat en un movimiento y medio
El siguiente paso es revertir el negro. Con este algoritmo pasé el mayor tiempo, se cometieron muchos errores antes de que todo funcionara correctamente.A primera vista, todo es similar a la versión anterior: para cada posición de la "línea blanca" es necesario ordenar todos los movimientos posibles del rey negro. Y agregue todas las combinaciones encontradas a la "línea negra": después de todo, este es un jaque mate en un movimiento y medio, desde el cual puede hacer un movimiento inverso para las blancas nuevamente, habrá un jaque mate en dos movimientos, y continúe hasta que se revisen todas las opciones.Ese fue el error. Con cualquier movimiento posible, las negras obtienen un jaque mate "cooperativo" en un movimiento y medio, pero en realidad el rey no necesariamente pasará por debajo del jaque mate. Dmitry Grin me señaló este error, que asistí a todos mis seminarios web sobre la creación de este programa, por lo que le agradezco por separado.El algoritmo correcto es el siguiente: para cada posición N después del movimiento inverso del rey negro, debe realizar todos los movimientos directos posibles para asegurarse de que todos conduzcan a posiciones familiares desde el "cuadro blanco", es decir, conduzcan a la colchoneta. Y solo después de esa posición N se puede agregar a la "línea negra". Y si el rey negro puede "escapar" de la posición N, entonces omitimos esta opción. Se reunirá en iteraciones posteriores, cuando habrá posiciones más familiares.Así es como se ve esta parte del algoritmo:
while (whiteQueue.Count > 0)
{
WhitesMove white = whiteQueue.Dequeue();
Combo whiteFigures = white.combo;
foreach (BlacksMove black in AllBlackBackMoves(white))
{
bool solved = true;
foreach (Coord blackKing in AllKingMoves(black.combo.blackKing))
{
whiteFigures.blackKing = blackKing;
if (isCheck(whiteFigures))
continue;
if (box.Exists(whiteFigures))
continue;
solved = false;
break;
}
if (solved)
blackQueue.Enqueue(black);
}
}
En total, se encontraron 156 combinaciones de "Mat y medio movimientos".Iterativo a mitad de camino
Los algoritmos descritos para crear medio paso deben estar en bucle. A partir de la "línea negra" formamos la "línea blanca", y luego viceversa: a partir de la línea "blanca" formamos la "línea negra". Y así sucesivamente hasta que se agoten todas las nuevas posiciones. El "cuadro blanco" se rellena en la etapa de formación de la "línea blanca", ya que coloca las posiciones en las que se mueve el blanco.El algoritmo listo para enumerar todas las opciones funcionó en algún lugar en 12 minutos y se detuvo en el movimiento 33. Esa es la cantidad máxima de movimientos necesarios para emparejar al rey negro con un caballo y un elefante desde cualquier posición.Por cierto, no había tantas posiciones "más difíciles", solo 156, aquí está una de ellas:
Mata no lo será!
Hay muchas posiciones en las que, incluso después del movimiento de las blancas, el rey negro puede comer un caballero u obispo y obtener un empate. También hay opciones de estancamiento. Estos son algunos de los artículos más interesantes.
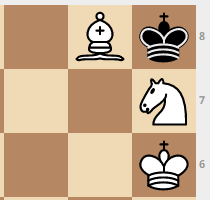
Cómo almacenar una base de datos de soluciones
¿Cómo almacenar la base de solución encontrada?La forma más fácil e incorrecta es usar la serialización. El conjunto de cuatro dimensiones serializado de la estructura tomó 1.7 gigabytes (!) De espacio en disco. El proceso de serialización duró aproximadamente seis minutos, la deserialización tomó casi lo mismo.Esta opción, por supuesto, no es adecuada. Además, en la práctica no es necesario utilizar toda la matriz de cuatro dimensiones. Solo se necesita una entrada para una línea de pedido específica.Eureka! Para ahorrar espacio, aún puede deshacerse del almacenamiento de las coordenadas de las figuras para cada combinación. Cuando tenemos una matriz de cuatro dimensiones, la posición de cada figura en el tablero está determinada únicamente por su índice en la matriz.Se decidió almacenar toda la base de datos de soluciones en un archivo, como un escaneo lineal de una matriz de cuatro dimensiones. Para cualquier posición posible, se calcula la dirección en la que se registra la respuesta correcta.¿Cómo registrar la respuesta que necesitamos de la forma más compacta posible? No es necesario almacenar la posición de las figuras, por lo que solo quedan tres números: cuántos movimientos al tapete, qué ir y dónde ir. Así es como se determina de manera única el movimiento correcto para las blancas.6 bit Cuántos movimientos al tapete es un número entero de 0 a 33.2bits. Qué figura camina: tres opciones posibles, un rey, un elefante o un caballo.6 bit A dónde va la pieza: el índice de campo en el tablero es de 0 a 63.Entonces, para cada registro de decisión, dos bytes son suficientes:1 byte: cuántos movimientos al tapete, o 0 si la posición no es familiar.2 bytes - FFNNNNNNFF - número de la figura a caminar (1 - rey, 2 - elefante, 3 - caballo)NNNNNN - coordenada de celda - a dónde ir (de 0 a 63).Entonces, el archivo de base de datos de la solución toma 64 * 32 * 64 * 64 palabras = exactamente 16 megabytes. La posición de las figuras se establece mediante las coordenadas de cada palabra, en el primer byte: el número de movimientos al tapete (o 0 si no hay solución), el segundo movimiento almacena el movimiento correcto.Sería posible reducir el tamaño del archivo a la mitad si no almacenaras el número de movimientos al tapete, pero no sería interesante jugar así.Coordenadas del elefante blanco cuadrado negro
Es hora de pagar por la optimización. Es necesario implementar un algoritmo de recálculo de coordenadas para combinaciones con un elefante "blanco y negro".Esto se hizo de la siguiente manera. Si la coordenada del elefante cae en un campo negro, entonces las coordenadas de todas las figuras en el tablero deben "voltearse". En este caso, la coordenada Y permanece sin cambios y X cambia a 7-X. Una demostración visual de un cambio de coordenadas, vea la figura.
Si el elefante está de pie sobre una jaula blanca, primero debe "voltear" las coordenadas de todas las figuras. Luego busque una posición en la base de datos de soluciones. Y una vez más "voltee" la coordenada del movimiento correcto leído desde allí.Visualización de la base de la solución.
Entonces, ¡el problema está resuelto!La base de datos de soluciones ha sido creada.¿Pero cómo demostrarlo?La forma más obvia es utilizar tecnologías web para que pueda dar un enlace a un ejemplo de trabajo. En mi "fórmula de programador", ya se creó el curso de fotografía " Nano-Chess ", donde utilizando las tecnologías de HTML, CSS, JavaScript y PHP se creó un tablero de ajedrez interactivo para jugar sin reglas para dos. Este guión fue tomado como base.Dejé solo cuatro piezas, eliminé la posibilidad de capturar, agregué funciones PHP para leer los movimientos correctos de la base de la solución y "respiré la vida" a través de JavaScript.En la página www.videosharp.info/chess puede experimentar con la base de datos de soluciones.
Para cada posición, los movimientos se calculan tanto para blanco como para negro.Para las blancas: el mejor movimiento que lleva al jaque mate.Para el negro: cuántos movimientos al tapete para cualquier movimiento posible.Puede hacer cualquier movimiento de las figuras con el mouse, no necesariamente según las reglas.El script calculará la opción para cualquier posición o escribirá que no hay opciones.Es interesante jugar, realizar los movimientos propuestos o mover las piezas a su discreción.Conclusión
Se realizó un gran trabajo interesante para resolver el problema del ajedrez.Si desea repetir de esta manera, puede ver videos sobre cómo crear este programa desde cero hasta el resultado con explicaciones detalladas y tareas independientes.Buena suerte